Betondeckung (Bsp.): Unterschied zwischen den Versionen
Gbolle (Diskussion | Beiträge) K |
|||
| (55 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | =Beispiel 1 - Stahlbetonträger im Außenbereich= | |
| − | + | == Aufgabenstellung == | |
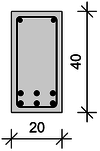
| − | == | + | Gegeben ist ein Stahlbeton-Unterzug im Außenbereich mit dem dargestellten Querschnitt. Für diesen Stahlbeton-Unterzug ist die [[Betondeckung (S***.de)|Betondeckung]] und die [[Statische Nutzhöhe|statische Nutzhöhe]] zu ermitteln. |
| − | |||
| − | [[File:Betondeckung (Bsp.) 1. | + | [[File:Betondeckung (Bsp.) 1.PNG|right|thumb|100px|Querschnitts- geometrie]] |
| − | + | ||
| − | + | Weitere Informationen: | |
| + | :{| | ||
| + | |- | ||
| + | | Beton: || C 25/30 (XC4) | ||
| + | |- | ||
| + | | untere Längsbewehrung: || 2 Lagen je 3 ø 16 | ||
| + | |- | ||
| + | | obere Längsbewehrung: || 2 ø 12 | ||
| + | |- | ||
| + | | Bügelbewehrung: || ø 8 | ||
| + | |} | ||
| − | + | == Lösung == | |
| − | + | === Mindestbetondeckung === | |
| − | + | Die Mindestbetondeckung ergibt sich als Maximalwert aus den nachfolgenden drei Bedingungen: | |
| − | |||
| − | + | :<math>c_\mathrm{min}=\mathrm{max}\begin{cases} | |
| − | |||
| − | |||
| − | <math>c_\mathrm{min}=\mathrm{max}\begin{cases} | ||
c_\mathrm{min,b} \\ | c_\mathrm{min,b} \\ | ||
c_\mathrm{min,dur} + \Delta c_\mathrm{dur,\lambda} - \Delta c_\mathrm{dur,st} - \Delta c_\mathrm{dur,add} \\ | c_\mathrm{min,dur} + \Delta c_\mathrm{dur,\lambda} - \Delta c_\mathrm{dur,st} - \Delta c_\mathrm{dur,add} \\ | ||
10\,\mathrm{mm} | 10\,\mathrm{mm} | ||
| − | \end{cases}</math><br /> | + | \end{cases}</math><br /><br /> |
| − | <br /> | + | |
| − | <math>c_\mathrm{min}=\mathrm{max}\begin{cases} | + | :<math>c_\mathrm{min}=\mathrm{max}\begin{cases} |
c_\mathrm{min,b} &= 16\,\mathrm{mm} \\ | c_\mathrm{min,b} &= 16\,\mathrm{mm} \\ | ||
25\,\mathrm{mm} + 0\,\mathrm{mm} - 0\,\mathrm{mm} - 0\,\mathrm{mm} &= \underline{25\,\mathrm{mm}}~~~\mathrm{(Korrosionsschutz~massg.)} \\ | 25\,\mathrm{mm} + 0\,\mathrm{mm} - 0\,\mathrm{mm} - 0\,\mathrm{mm} &= \underline{25\,\mathrm{mm}}~~~\mathrm{(Korrosionsschutz~massg.)} \\ | ||
10\,\mathrm{mm} &= 10\,\mathrm{mm} | 10\,\mathrm{mm} &= 10\,\mathrm{mm} | ||
| − | \end{cases}</math><br /> | + | \end{cases}</math><br /><br /> |
| + | |||
| + | === Vorhaltemaß === | ||
| + | Da der Korrosionsschutz maßgebend ist und das Bauteil nicht in der Expositionsklasse XC 1 liegt, ergibt sich folgender Wert für das Vorhaltemaß. | ||
| + | |||
| + | :<math>\Delta c_\mathrm{dev}=\underline{15\,\mathrm{mm}}</math><br /><br /> | ||
| + | |||
| + | === Nennmaß der Betondeckung === | ||
| + | Das Nennmaß der Betondeckung ergibt sich wie folgt: | ||
| + | |||
| + | :<math>c_\mathrm{nom}=c_\mathrm{min} + \Delta c_\mathrm{dev} =25\,\mathrm{mm} + 15\,\mathrm{mm}=\underline{40\,\mathrm{mm}}</math><br /><br /> | ||
| + | |||
| + | === Verlegemaß der Bewehrung === | ||
| + | Das Verlegemaß der Bewehrung ergibt sich aus dem Nennmaß der Betondeckung - aufgerundet auf volle 5 mm. | ||
| + | |||
| + | :<math>c_\mathrm{V}=c_\mathrm{nom}=\underline{40\,\mathrm{mm}}</math><br /><br /> | ||
| + | |||
| + | === Abstand der Schwerachse der Biegezugbewehrung zum naheliegenden Rand === | ||
| + | ==== untere Längsbewehrung (zweilagig) ==== | ||
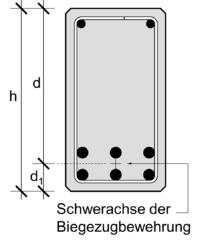
| + | [[File:Betondeckung (Bsp.) 3.png|right|thumb|200px|Abstand der Schwerachse der Bewehrung zum naheliegenden Rand d<sub>1</sub>]] | ||
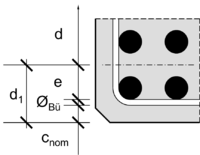
| + | [[File:Betondeckung (Bsp.) 4.png|right|thumb|200px|Zusammensetzung des Maßes d<sub>1</sub>]] | ||
| − | + | Der Abstand d<sub>1</sub> von der Schwerachse der Bewehrung zum naheliegenden Rand wird in den Berechnungen der mb-AEC-Baustatikmodule auch mit d'<sub>u</sub> (für eine untere Biegezugbewehrung) bzw. d'<sub>o</sub> (für eine obere Biegezugbewehrung) bezeichnet. | |
<br /> | <br /> | ||
| − | <math> | + | |
| − | ==== | + | :<math>d_{ 1 }=d'_{ u }=c_{ V }+\varnothing_{ Bue }+e=40+8+\frac{ 3 \cdot 201 \cdot 44+3 \cdot 201 \cdot 8 }{ 6 \cdot 201 }= \underline{74 mm}</math> |
| + | |||
| + | ==== obere Längsbewehrung (einlagig) ==== | ||
| + | :<math>d_{ 2 }=d'_{ o }=c_{ V }+ \varnothing_{ Bue } + e = 40 + 8 + 0,5 \cdot 12 = \underline{ 54 mm }</math><br /> | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | === Ermittlung der statischen Nutzhöhe d === |
| − | + | ==== untere Längsbewehrung (zweilagig) ==== | |
| − | + | :<math>d=h-d_{ 1 }=400-74=326mm=\underline{ 32,6 cm }</math><br /> | |
| − | <math>d=h - | + | |
| − | + | ==== obere Längsbewehrung (einlagig) ==== | |
| − | + | :<math>d=h-d_{ 2 }=400-54=346mm=\underline{ 34,6 cm }</math><br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math>d=h - | ||
| − | |||
| − | |||
<br /> | <br /> | ||
| − | |||
| − | + | == Vergleich mit mb-AEC Baustatik == | |
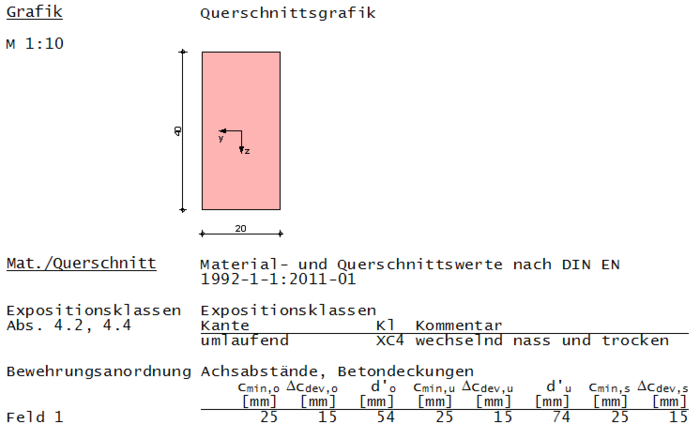
| − | Bei Eingabe der oben vorgegebenen Werte | + | Bei Eingabe der oben vorgegebenen Werte (Querschnittsgeometrie, Bewehrungsdurchmesser, Expositionsklasse) ergeben sich die folgenden Berechnungsergebnisse:<br /> |
<br /> | <br /> | ||
[[File:Betondeckung (Bsp.) 2.PNG|rahmenlos|rand|tumb|700px|Ausdruck vom Modul S340.de]] | [[File:Betondeckung (Bsp.) 2.PNG|rahmenlos|rand|tumb|700px|Ausdruck vom Modul S340.de]] | ||
| − | == | + | {{Seiteninfo(mb) |
| − | + | |Quality-flag = [[File:quality-flag-green.gif|right|70px]] | |
| − | + | |Status = Seite geprüft, inhaltlich OK| | |
| − | + | |Modul-Version = 2014.011 | |
| − | + | }} | |
| − | [[Kategorie:Beispiele]] | + | [[Kategorie:Beispiele-Stahlbetonbau]] |
Version vom 5. Juni 2019, 11:47 Uhr
Beispiel 1 - Stahlbetonträger im Außenbereich
Aufgabenstellung
Gegeben ist ein Stahlbeton-Unterzug im Außenbereich mit dem dargestellten Querschnitt. Für diesen Stahlbeton-Unterzug ist die Betondeckung und die statische Nutzhöhe zu ermitteln.
Weitere Informationen:
Beton: C 25/30 (XC4) untere Längsbewehrung: 2 Lagen je 3 ø 16 obere Längsbewehrung: 2 ø 12 Bügelbewehrung: ø 8
Lösung
Mindestbetondeckung
Die Mindestbetondeckung ergibt sich als Maximalwert aus den nachfolgenden drei Bedingungen:
Vorhaltemaß
Da der Korrosionsschutz maßgebend ist und das Bauteil nicht in der Expositionsklasse XC 1 liegt, ergibt sich folgender Wert für das Vorhaltemaß.
Nennmaß der Betondeckung
Das Nennmaß der Betondeckung ergibt sich wie folgt:
Verlegemaß der Bewehrung
Das Verlegemaß der Bewehrung ergibt sich aus dem Nennmaß der Betondeckung - aufgerundet auf volle 5 mm.
Abstand der Schwerachse der Biegezugbewehrung zum naheliegenden Rand
untere Längsbewehrung (zweilagig)
Der Abstand d1 von der Schwerachse der Bewehrung zum naheliegenden Rand wird in den Berechnungen der mb-AEC-Baustatikmodule auch mit d'u (für eine untere Biegezugbewehrung) bzw. d'o (für eine obere Biegezugbewehrung) bezeichnet.
obere Längsbewehrung (einlagig)
Ermittlung der statischen Nutzhöhe d
untere Längsbewehrung (zweilagig)
obere Längsbewehrung (einlagig)
Vergleich mit mb-AEC Baustatik
Bei Eingabe der oben vorgegebenen Werte (Querschnittsgeometrie, Bewehrungsdurchmesser, Expositionsklasse) ergeben sich die folgenden Berechnungsergebnisse:
Seiteninfo
|