Verankerung am Einzelfundament (Bsp.): Unterschied zwischen den Versionen
| Zeile 44: | Zeile 44: | ||
<math> {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5kN/cm^2 \cdot \frac{11,82cm^2}{32,16cm^2} = 15,99kN/cm^2 </math> | <math> {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5kN/cm^2 \cdot \frac{11,82cm^2}{32,16cm^2} = 15,99kN/cm^2 </math> | ||
| + | |||
| + | === Grundwert der Verankerungslänge === | ||
| + | <math> l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}} = \frac{1,6 cm}{4} \cdot \frac{15,99 kN/cm^2}{0,232 kN/cm^2} = 27,57 cm</math> | ||
| + | |||
| + | === Ersatzverankerungslänge === | ||
| + | <math>l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}</math> | ||
| + | |||
| + | Formgebung: Gerades Stabende → <math>{\alpha}_1 = 1,0</math> | ||
| + | |||
| + | Angeschweißte Querstäbe: Keine → <math>{\alpha}_4 = 1,0</math> | ||
| + | |||
| + | Querdruck: Vernachlässigbar → <math>{\alpha}_5 = 1,0</math> | ||
| + | |||
| + | <math>l_{b,eq} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 27,57 cm = 27,57 cm</math> | ||
| + | |||
| + | === Mindestverankerungslänge === | ||
| + | <math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> | ||
| + | |||
| + | <math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1,0 \cdot \left( \frac{1,6 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,232 kN/cm^2} \right) \\ 10 \cdot 1,0 \cdot 1,6 cm \end{matrix}} \right\} </math> | ||
| + | |||
| + | <math>l_{b,min} = max\left\{ {\begin{matrix} 22,5 cm \\ 16 cm \end{matrix}} \right\} </math> | ||
| + | |||
| + | → <math> l_{b,eq} = 27,57 cm </math> | ||
| + | |||
| + | === Nachweis der Verankerungslänge === | ||
| + | <math>l_{b,vorh} = x - c_{nom} = 30 cm - 5,5 cm = 24,5 cm</math> | ||
| + | |||
| + | <math>l_{b,eq} = 27,57 cm \leq 24,5 cm = l_{b,vorh}</math> | ||
| + | |||
| + | → Verankerung mit geradem Stabende nicht möglich. | ||
| + | |||
| + | |||
| + | == Verankerung nach allgemeiner Theorie == | ||
| + | === Versatzmaß === | ||
| + | Für Bauteile ohne Querkraftbewehrung gilt nach EC 2 9.2.1.3(2): | ||
| + | |||
| + | <math> a_L = d = 54 cm </math> | ||
| + | |||
| + | === Moment am Beginn der Verankerungslänge === | ||
| + | Die Verankerungslänge für den Haken beginnt an der Biegung. Der Mindestbiegerollendurchmesser beträgt nach EC 2 Tab. 8.1DE für <math> \O_s < 20 mm </math> → <math> D_{min} = 4 \cdot \O_s </math>. | ||
Version vom 3. April 2022, 08:16 Uhr
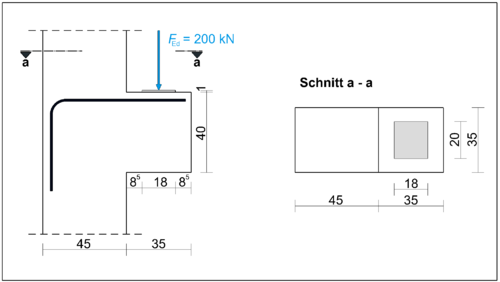
Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten
Aufgabenstellung
Für das dargestellte Einzelfundament ist die Verankerungslänge der Biegezugbewehrung zu bestimmen. Gegeben sind folgende Daten:
- Beton C20/25
- Betonstahlstahl B500B
- Betondeckung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_{nom} = 55 mm}
- Gewählte Bewehrung insgesamt in x-Richtung: 16 Ø 16 mm
Verankerung mit geradem Stabende nach EC 2
Verbundfestigkeit
Bewehrung unten → guter Verbund
→ C20/25 → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{bd} = 2,32 N/mm^2 = 0,32 kN/cm^2}
Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{min} = \frac{h}{2} = \frac{0,6m}{2} = 0,3m }
Sohlspannung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{0} = \frac{N_{Ed}}{b_x} = \frac{2.100kN}{3,0m} = 700 kN/m }
Resultierende der Sohlspannung unter der Verankerungslänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R = {\sigma}_{0} \cdot x = 700 kN/m \cdot 0,3m = 210kN }
Hebelarm der Resultierenden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_e = \frac{b_x}{2} - \frac{x}{2} = \frac{3,0m}{2} - \frac{0,6m}{2} = 1,20m }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_i = 0,9 \cdot d_x = 0,9 \cdot 0,54 m = 0,49 m }
Zugkraft
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = R \cdot \frac{z_e}{z_i} = 210 kN \cdot \frac{1,20m}{0,49m} = 514,29kN }
Erforderliche Bewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = \frac{F_{sd}}{f_{yd}} = \frac{514,29kN}{43,5kN/cm^2} = 11,82 cm^2}
Stahlspannung
Gegeben sind 16 Ø 16 → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 32,16cm^2 } :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5kN/cm^2 \cdot \frac{11,82cm^2}{32,16cm^2} = 15,99kN/cm^2 }
Grundwert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}} = \frac{1,6 cm}{4} \cdot \frac{15,99 kN/cm^2}{0,232 kN/cm^2} = 27,57 cm}
Ersatzverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
Formgebung: Gerades Stabende → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 1,0}
Angeschweißte Querstäbe: Keine → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_4 = 1,0}
Querdruck: Vernachlässigbar → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5 = 1,0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 27,57 cm = 27,57 cm}
Mindestverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1,0 \cdot \left( \frac{1,6 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,232 kN/cm^2} \right) \\ 10 \cdot 1,0 \cdot 1,6 cm \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 22,5 cm \\ 16 cm \end{matrix}} \right\} }
→ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 27,57 cm }
Nachweis der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,vorh} = x - c_{nom} = 30 cm - 5,5 cm = 24,5 cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 27,57 cm \leq 24,5 cm = l_{b,vorh}}
→ Verankerung mit geradem Stabende nicht möglich.
Verankerung nach allgemeiner Theorie
Versatzmaß
Für Bauteile ohne Querkraftbewehrung gilt nach EC 2 9.2.1.3(2):
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_L = d = 54 cm }
Moment am Beginn der Verankerungslänge
Die Verankerungslänge für den Haken beginnt an der Biegung. Der Mindestbiegerollendurchmesser beträgt nach EC 2 Tab. 8.1DE für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \O_s < 20 mm } → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D_{min} = 4 \cdot \O_s } .