Verankerung am Einzelfundament (Bsp.): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten | Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten | ||
| + | |||
| + | == Kontext == | ||
| + | |||
| + | In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Rand eines Einzelfundaments nachzuweisen. Hierzu wird zunächst die Verankerung mit geradem Stabende nach dem Berechnungsmodell im EC2 versucht. Falls dies nicht gelingt, wird die Verankerungslänge durch Verschieben der Belastung ermittelt. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zu Einzelfundamenten finden sich [[Verankerungslänge#Verankerung_am_Rand_von_Einzelfundamenten|hier]] | ||
| + | |||
== Aufgabenstellung == | == Aufgabenstellung == | ||
| Zeile 5: | Zeile 10: | ||
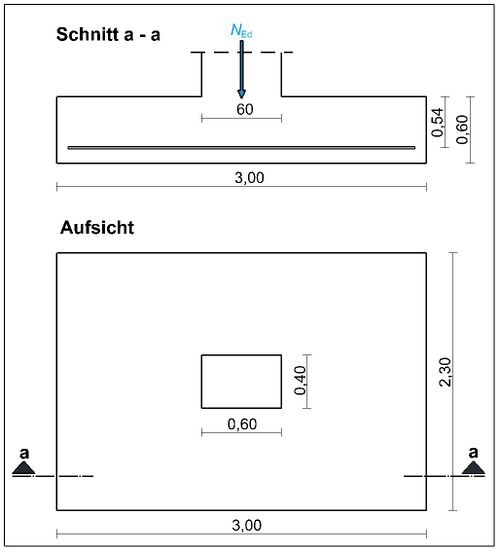
[[File:Verankerung am Einzelfundament (Bsp.) 1.JPG|rahmenlos|rand|tumb|500px|Baustatik-Wiki]] | [[File:Verankerung am Einzelfundament (Bsp.) 1.JPG|rahmenlos|rand|tumb|500px|Baustatik-Wiki]] | ||
| − | Für das dargestellte Einzelfundament ist die Verankerungslänge der Biegezugbewehrung zu bestimmen. Gegeben sind folgende Daten: | + | Für das dargestellte Einzelfundament ist die Verankerungslänge der Biegezugbewehrung zu bestimmen. |
| + | |||
| + | Gegeben sind folgende Daten: | ||
* Beton C20/25 | * Beton C20/25 | ||
| Zeile 116: | Zeile 123: | ||
Angeschweißte Querstäbe: Keine → <math>{\alpha}_4 = 1,0</math> | Angeschweißte Querstäbe: Keine → <math>{\alpha}_4 = 1,0</math> | ||
| − | Querdruck: | + | Querdruck: In einem Einzelfundament wirken entlang beider Achsen Zugkräfte. In diesem Beispiel wird die Verankerung in x-Richtung nachgewiesen. Damit wirken die Zugkräfte in y-Richtung als Querzug auf den zu verankernden Stab → <math>{\alpha}_5 = 1,5</math> |
| − | <math>l_{bd} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 1, | + | <math>l_{bd} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 1,5 \cdot 14,23 cm = 21,35 cm</math> |
=== Mindestverankerungslänge === | === Mindestverankerungslänge === | ||
<math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> | <math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> | ||
| − | <math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1, | + | <math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1,5 \cdot \left( \frac{1,6 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,232 kN/cm^2} \right) \\ 10 \cdot 1,5 \cdot 1,6 cm \end{matrix}} \right\} </math> |
| − | <math>l_{b,min} = max\left\{ {\begin{matrix} | + | <math>l_{b,min} = max\left\{ {\begin{matrix} 33,75 cm \\ 24 cm \end{matrix}} \right\} </math> |
| − | → <math> l_{bd} = | + | → <math> l_{bd} = 33,75 cm </math> |
=== Nachweis der Verankerungslänge === | === Nachweis der Verankerungslänge === | ||
| − | Als Länge des geraden Winkelhakenschenkels wird <math> l = | + | Als Länge des geraden Winkelhakenschenkels wird <math> l = 20 \cdot \O_s </math> gewählt. |
| − | <math>l_{b,vorh} = l + \O_s + D_{min} / 2 = | + | <math>l_{b,vorh} = l + \O_s + D_{min} / 2 = 32 cm + 1,6 cm + 3,2 cm = 36,8 cm</math> |
| − | <math>l_{bd} = | + | <math>l_{bd} = 33,75 cm \leq 36,8 cm = l_{b,vorh}</math> |
→ Nachweis der Verankerung mit Winkelhaken erfüllt. | → Nachweis der Verankerung mit Winkelhaken erfüllt. | ||
Version vom 1. Mai 2022, 20:26 Uhr
Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten
Kontext
In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Rand eines Einzelfundaments nachzuweisen. Hierzu wird zunächst die Verankerung mit geradem Stabende nach dem Berechnungsmodell im EC2 versucht. Falls dies nicht gelingt, wird die Verankerungslänge durch Verschieben der Belastung ermittelt. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zu Einzelfundamenten finden sich hier
Aufgabenstellung
Für das dargestellte Einzelfundament ist die Verankerungslänge der Biegezugbewehrung zu bestimmen.
Gegeben sind folgende Daten:
- Beton C20/25
- Betonstahlstahl B500B
- Betondeckung:
- Gewählte Bewehrung insgesamt in x-Richtung: 16 Ø 16 mm
- Einwirkende Normalkraft:
Verankerung mit geradem Stabende nach EC 2
Verbundfestigkeit
Bewehrung unten → guter Verbund
→ C20/25 →
Abstand
Sohlspannung
Resultierende der Sohlspannung unter der Verankerungslänge
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle R={\sigma }_{0}\cdot x=700kN/m\cdot 0,3m=210kN}
Hebelarm der Resultierenden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_i = 0,9 \cdot d_x = 0,9 \cdot 0,54 m = 0,49 m }
Zugkraft
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = R \cdot \frac{z_e}{z_i} = 210 kN \cdot \frac{1,20m}{0,49m} = 514,29kN }
Erforderliche Bewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = \frac{F_{sd}}{f_{yd}} = \frac{514,29kN}{43,5kN/cm^2} = 11,82 cm^2}
Stahlspannung
Gegeben sind 16 Ø 16 → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 32,16cm^2 } :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5kN/cm^2 \cdot \frac{11,82cm^2}{32,16cm^2} = 15,99kN/cm^2 }
Grundwert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}} = \frac{1,6 cm}{4} \cdot \frac{15,99 kN/cm^2}{0,232 kN/cm^2} = 27,57 cm}
Ersatzverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
Formgebung: Gerades Stabende → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 1,0}
Angeschweißte Querstäbe: Keine →
Querdruck: Vernachlässigbar → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5 = 1,0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 27,57 cm = 27,57 cm}
Mindestverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1,0 \cdot \left( \frac{1,6 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,232 kN/cm^2} \right) \\ 10 \cdot 1,0 \cdot 1,6 cm \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 22,5 cm \\ 16 cm \end{matrix}} \right\} }
→ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 27,57 cm }
Nachweis der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 27,57 cm \leq 24,5 cm = l_{b,vorh}}
→ Verankerung mit geradem Stabende nicht möglich.
Verankerung nach allgemeiner Theorie
Versatzmaß
Für Bauteile ohne Querkraftbewehrung gilt nach EC 2 9.2.1.3(2):
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_L = d = 54 cm }
Moment am Beginn der Verankerungslänge
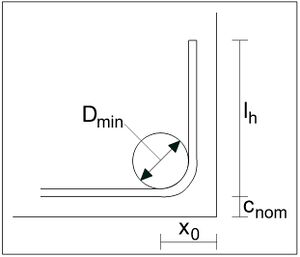
Die Verankerungslänge für den Haken beginnt an der Biegung. Der Mindestbiegerollendurchmesser beträgt nach EC 2 Tab. 8.1DE für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \O_s < 20 mm } → .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D_{min} = 4 \cdot \O_s = 4 \cdot 1,6cm =6,4cm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_0 = c_{nom} + \O_s + D_{min} / 2 = 5,5cm + 1,6 cm + 6,4cm / 2 = 10,3cm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed,x0} = \frac{N_{Ed}}{b_x} \cdot \frac{(x_0 + a_L)^2}{2} = \frac{2.100kN}{3,0m} \cdot \frac{(0,1m + 0,54m)^2}{2} = 143,36kNm }
Randzugkraft
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = \frac{M_{Ed,x0}}{z} = \frac{143,36kNm}{0,54m} = 265,48kN }
Erforderliche Bewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = \frac{F_{sd}}{f_{yd}} = \frac{265,48kN}{43,5kN/cm^2} = 6,10cm^2}
Stahlspannung
Gegeben sind 16 Ø 16 → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 32,16cm^2 } :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5kN/cm^2 \cdot \frac{6,10cm^2}{32,16cm^2} = 8,25kN/cm^2 }
Grundwert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}} = \frac{1,6 cm}{4} \cdot \frac{8,25 kN/cm^2}{0,232 kN/cm^2} = 14,23 cm}
Bemessungswert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = {\alpha}_1 \cdot {\alpha}_3 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
Formgebung: Gerades Stabende → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 1,0}
Querbewehrung: Vernachlässigbar → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_3 = 1,0}
Angeschweißte Querstäbe: Keine → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_4 = 1,0}
Querdruck: In einem Einzelfundament wirken entlang beider Achsen Zugkräfte. In diesem Beispiel wird die Verankerung in x-Richtung nachgewiesen. Damit wirken die Zugkräfte in y-Richtung als Querzug auf den zu verankernden Stab → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5 = 1,5}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 1,5 \cdot 14,23 cm = 21,35 cm}
Mindestverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1,5 \cdot \left( \frac{1,6 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,232 kN/cm^2} \right) \\ 10 \cdot 1,5 \cdot 1,6 cm \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 33,75 cm \\ 24 cm \end{matrix}} \right\} }
→ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = 33,75 cm }
Nachweis der Verankerungslänge
Als Länge des geraden Winkelhakenschenkels wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l = 20 \cdot \O_s } gewählt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,vorh} = l + \O_s + D_{min} / 2 = 32 cm + 1,6 cm + 3,2 cm = 36,8 cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = 33,75 cm \leq 36,8 cm = l_{b,vorh}}
→ Nachweis der Verankerung mit Winkelhaken erfüllt.