Zugkraftdeckung: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
Unter Zugkraftdeckung versteht man die Ermittlung der statisch notwendigen Menge der Biegezugbewehrung, bezogen auf die Längsachse des Biegebauteils. Man spricht dabei vom Anpassen der Biegezugbewehrung an den Zugkraftverlauf. Durch den Nachweis der Zugkraftdeckung wird sichergestellt, dass in jedem Querschnitt die auftretende Zuggurtkraft durch die vorhandene Bewehrung aufgenommen werden kann.<ref Name = "Stahlbeton for Beginners">Scheerer, S; Proske, D: Stahlbeton for Beginners, Grundlagen für die Bemessung und Konstruktion, 2. Auflage, Springer-Verlag, 2008</ref> | Unter Zugkraftdeckung versteht man die Ermittlung der statisch notwendigen Menge der Biegezugbewehrung, bezogen auf die Längsachse des Biegebauteils. Man spricht dabei vom Anpassen der Biegezugbewehrung an den Zugkraftverlauf. Durch den Nachweis der Zugkraftdeckung wird sichergestellt, dass in jedem Querschnitt die auftretende Zuggurtkraft durch die vorhandene Bewehrung aufgenommen werden kann.<ref Name = "Stahlbeton for Beginners">Scheerer, S; Proske, D: Stahlbeton for Beginners, Grundlagen für die Bemessung und Konstruktion, 2. Auflage, Springer-Verlag, 2008</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
=Problemstellung und Einführung in die Thematik= | =Problemstellung und Einführung in die Thematik= | ||
Wird die Menge der Biegezugbewehrung für ein biegebeanspruchtes Stahlbetonbauteil ermittelt, so ist hierfür an erster Stelle, das maximal wirkende Biegemoment maßgebend. Dieses befindet sich in der Regel, je nach statischem System, in Feldmitte (Feldmoment), im Bereich von Zwischenauflagern (Stützmoment) oder auch im Anschnitt eines Kragarms. Die weiteren Abschnitte entlang der Bauteilachse, in denen geringere Biegemomente wirken, sind für die reine Biegebemessung somit nicht relevant und bleiben hierbei unberücksichtigt. Eine Variante der Bewehrungsführung wäre nun, die für das maximale Biegemoment ermittelte Bewehrungsmenge, über die gesamte Bauteillänge unverändert in der entsprechenden Bauteilebene anzuordnen. Diese Variante der Bewehrungsführung kommt in der Praxis auch durchaus in vielen Fällen zur Anwendung. Der entscheidende Nachteil hierbei ist jedoch, dass je nach Bauteilgröße eine teilweise wesentlich höhere Bewehrungsstahlmenge verbaut wird, als tatsächlich nötig wäre. Grund dafür ist die Tatsache, dass auf der gesamten Bauteillänge eine einheitliche Bewehrungsmenge angeordnet wird, welche auf das maximale Biegemoment abgestimmt ist. Betrachtet man jedoch den Momentenverlauf im Bauteil, so fällt dieser ja nach dem maximalen Moment mit einem linearen oder parabolischen Verlauf ab. Daraus lässt sich herleiten, dass die weniger stark beanspruchten Bauteilbereiche somit auch weniger Bewehrungsstahl benötigen. Hierbei kann das Verfahren der Zugkraftdeckung angewendet werden. Man spricht dabei vom Anpassen der Biegezugbewehrung an den Zugkraftverlauf. Eine Ähnliche Vorgehensweise findet man im Stahlbetonbau auch bei der Querkraftbemessung. Hier wird über die Querkraftdeckung die Querkraftbewehrung an den Verlauf der Querkraft angepasst.<ref Name = "Stahlbeton for Beginners"></ref><ref Name = "Springer">Bindseil, P.: Massivbau: Bemessung und Konstruktion im Stahlbetonbau mit Beispielen, 5. Auflage, Springer Vieweg Verlag, 2015</ref><ref Name = "Teubner">Gottfried C.O. Lohmeyer (Hrsg.): Stahlbetonbau, Bemessung - Konstruktion - Ausführung, 6. Auflage, Teubner Verlag</ref> | Wird die Menge der Biegezugbewehrung für ein biegebeanspruchtes Stahlbetonbauteil ermittelt, so ist hierfür an erster Stelle, das maximal wirkende Biegemoment maßgebend. Dieses befindet sich in der Regel, je nach statischem System, in Feldmitte (Feldmoment), im Bereich von Zwischenauflagern (Stützmoment) oder auch im Anschnitt eines Kragarms. Die weiteren Abschnitte entlang der Bauteilachse, in denen geringere Biegemomente wirken, sind für die reine Biegebemessung somit nicht relevant und bleiben hierbei unberücksichtigt. Eine Variante der Bewehrungsführung wäre nun, die für das maximale Biegemoment ermittelte Bewehrungsmenge, über die gesamte Bauteillänge unverändert in der entsprechenden Bauteilebene anzuordnen. Diese Variante der Bewehrungsführung kommt in der Praxis auch durchaus in vielen Fällen zur Anwendung. Der entscheidende Nachteil hierbei ist jedoch, dass je nach Bauteilgröße eine teilweise wesentlich höhere Bewehrungsstahlmenge verbaut wird, als tatsächlich nötig wäre. Grund dafür ist die Tatsache, dass auf der gesamten Bauteillänge eine einheitliche Bewehrungsmenge angeordnet wird, welche auf das maximale Biegemoment abgestimmt ist. Betrachtet man jedoch den Momentenverlauf im Bauteil, so fällt dieser ja nach dem maximalen Moment mit einem linearen oder parabolischen Verlauf ab. Daraus lässt sich herleiten, dass die weniger stark beanspruchten Bauteilbereiche somit auch weniger Bewehrungsstahl benötigen. Hierbei kann das Verfahren der Zugkraftdeckung angewendet werden. Man spricht dabei vom Anpassen der Biegezugbewehrung an den Zugkraftverlauf. Eine Ähnliche Vorgehensweise findet man im Stahlbetonbau auch bei der Querkraftbemessung. Hier wird über die Querkraftdeckung die Querkraftbewehrung an den Verlauf der Querkraft angepasst.<ref Name = "Stahlbeton for Beginners"></ref><ref Name = "Springer">Bindseil, P.: Massivbau: Bemessung und Konstruktion im Stahlbetonbau mit Beispielen, 5. Auflage, Springer Vieweg Verlag, 2015</ref><ref Name = "Teubner">Gottfried C.O. Lohmeyer (Hrsg.): Stahlbetonbau, Bemessung - Konstruktion - Ausführung, 6. Auflage, Teubner Verlag</ref> | ||
| − | Ziel ist es vereinfachend gesagt, den Materialeinsatz in Form von Bewehrungsstahl an die | + | Ziel ist es vereinfachend gesagt, den Materialeinsatz in Form von Bewehrungsstahl an die vom Momentenverlauf abhängige Stahlzugkraft anzupassen. Ähnliche Beispiele sind im Stahl- oder Holzbau zu finden. Zum Beispiel beim sogenannten „Fischbauchträger“. Dort wird die Bauteilkontur entsprechend des Momentenverlaufes gestaltet. |
=Normung und Anwendung= | =Normung und Anwendung= | ||
| − | Geregelt ist das Verfahren der Zugkraftdeckung im Eurocode 2 (DIN EN 1992-1-1 mit Nationalem Anhang) im Kapitel 9 (Konstruktionsregeln)<ref Name = "EC2">Eurocode 2: DIN EN 1992-1-1 mit Nationalem Anhang (2. Auflage):Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau - Konstruktionsregeln</ref> . Im Unterschied zur | + | Geregelt ist das Verfahren der Zugkraftdeckung im Eurocode 2 (DIN EN 1992-1-1 mit Nationalem Anhang) im Kapitel 9 (Konstruktionsregeln)<ref Name = "EC2">Eurocode 2: DIN EN 1992-1-1 mit Nationalem Anhang (2. Auflage):Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau - Konstruktionsregeln</ref> . Im Unterschied zur DIN 1045-1 darf mit der Einführung des Eurocodes nun auch als zusätzliche Variante ein linearer Kraftverlauf entlang der Verankerungslänge bei der Abdeckung der Zugkraftlinie durch gestaffelte Bewehrung berücksichtigt werden (siehe [[#Variantenvergleich Zugkraftdeckungslinien|'''Variantenvergleich Zugkraftdeckungslinien''']]).<ref Name = "EC2"></ref> |
Anwendung findet das Verfahren der Zugkraftdeckung bei verschiedensten biegebeanspruchten Stahlbetonbauteilen. Insbesondere Balken, Platten, Plattenbalken und Stützen. Also Bauteile, bei welchen es aus wirtschaftlichen- oder platztechnischen Gründen sinnvoll ist, die Biegezugbewehrung an den Zugkraftverlauf anzupassen und entsprechend abzustufen. Die hieraus resultierenden Vorteile sind die Einsparung von Bewehrungsstahl und damit verknüpft auch ein Platzgewinn für anderweitige Bewehrungselemente in Bauteilen mit einem hohen Bewehrungsgrad.<ref Name = "Stahlbeton for Beginners"></ref> | Anwendung findet das Verfahren der Zugkraftdeckung bei verschiedensten biegebeanspruchten Stahlbetonbauteilen. Insbesondere Balken, Platten, Plattenbalken und Stützen. Also Bauteile, bei welchen es aus wirtschaftlichen- oder platztechnischen Gründen sinnvoll ist, die Biegezugbewehrung an den Zugkraftverlauf anzupassen und entsprechend abzustufen. Die hieraus resultierenden Vorteile sind die Einsparung von Bewehrungsstahl und damit verknüpft auch ein Platzgewinn für anderweitige Bewehrungselemente in Bauteilen mit einem hohen Bewehrungsgrad.<ref Name = "Stahlbeton for Beginners"></ref> | ||
| Zeile 18: | Zeile 14: | ||
==Grundvoraussetzungen für das Anwenden der Zugkraftdeckung== | ==Grundvoraussetzungen für das Anwenden der Zugkraftdeckung== | ||
Im Allgemeinen genügt beim Nachweis der Zugkraftdeckung das Betrachten des Grenzzustandes der Tragfähigkeit. Werden jedoch Biegemomente mehr als 15% bei Linear-elastischer Berechnung umgelagert oder es kommt durch Verfahren der Schnittgrößenermittlung mit der Plastizitätstheorie/Nichtlineare Verfahren zu erheblichen Verschiebungen der Momentennullpunkte zwischen GZG und GZT, so ist der Nachweis ebenfalls für den Grenzzustand der Gebrauchstauglichkeit zu führen.<ref Name = "EC2"></ref> | Im Allgemeinen genügt beim Nachweis der Zugkraftdeckung das Betrachten des Grenzzustandes der Tragfähigkeit. Werden jedoch Biegemomente mehr als 15% bei Linear-elastischer Berechnung umgelagert oder es kommt durch Verfahren der Schnittgrößenermittlung mit der Plastizitätstheorie/Nichtlineare Verfahren zu erheblichen Verschiebungen der Momentennullpunkte zwischen GZG und GZT, so ist der Nachweis ebenfalls für den Grenzzustand der Gebrauchstauglichkeit zu führen.<ref Name = "EC2"></ref> | ||
| + | Im folgenden wird von einer Schnittgrößenermittlung nach dem linear-elastischen Verfahren ohne Momentenumlagerung ausgegangen. | ||
| + | |||
*'''Bewehrungsmengen für die maßgebenden Biegemomente''' | *'''Bewehrungsmengen für die maßgebenden Biegemomente''' | ||
::Die Anzahl und Durchmesser der Bewehrungsstäbe (Biegezugbewehrung) für die maßgebenden Biegemomente entsprechend der Biegebemessung müssen für die Zugkraftdeckung bekannt sein. | ::Die Anzahl und Durchmesser der Bewehrungsstäbe (Biegezugbewehrung) für die maßgebenden Biegemomente entsprechend der Biegebemessung müssen für die Zugkraftdeckung bekannt sein. | ||
| Zeile 23: | Zeile 21: | ||
::Der Querkraftverlauf und die Druckstrebenneigungswinkel aus der Querkraftbemessung sind für die Zugkraftdeckung erforderlich. | ::Der Querkraftverlauf und die Druckstrebenneigungswinkel aus der Querkraftbemessung sind für die Zugkraftdeckung erforderlich. | ||
*'''Momentengrenzlinie (Umhüllende)''' | *'''Momentengrenzlinie (Umhüllende)''' | ||
| − | Anders als bei der reinen Biegebemessung sind bei der Zugkraftdeckung nicht nur die Einzelwerte der Momente an den maßgebenden Extremstellen relevant, sondern die gesamte Momentengrenzlinie. | + | ::Anders als bei der reinen Biegebemessung sind bei der Zugkraftdeckung nicht nur die Einzelwerte der Momente an den maßgebenden Extremstellen relevant, sondern die gesamte Momentengrenzlinie. |
| − | |||
| − | |||
| + | :*Erläuterung - Momentengrenzlinie: | ||
| + | [[Datei:Zugkraftdeckung 2.png|mini|150px|right|Momentenausrundung am Zwischenauflager<ref Name = "Vorlesungsunterlagen"></ref> ]] | ||
:::Die maßgebenden Biegemomente an einem statischen System resultieren aufgrund unterschiedlicher Laststellungen (siehe Grafik). Das maßgebende Feldmoment an einem Durchlaufträger entsteht z.B. aufgrund einer anderen Laststellung als für das maßgebende Stützmoment. Legt man die Momentenlinien der jeweiligen Lastfälle für die maßgebenden Bemessungsmomente übereinander und betrachtet die umhüllende Außenkontur, so erhält man die Momentengrenzlinie der Bemessungswerte. Die Momentengrenzlinie besteht somit aus bereichsweisen verschieden zusammengesetzten Funktionen. Somit ist diese keine „glatte Funktion“ und kann dementsprechend Knickstellen enthalten.<ref Name = "Springer"></ref> | :::Die maßgebenden Biegemomente an einem statischen System resultieren aufgrund unterschiedlicher Laststellungen (siehe Grafik). Das maßgebende Feldmoment an einem Durchlaufträger entsteht z.B. aufgrund einer anderen Laststellung als für das maßgebende Stützmoment. Legt man die Momentenlinien der jeweiligen Lastfälle für die maßgebenden Bemessungsmomente übereinander und betrachtet die umhüllende Außenkontur, so erhält man die Momentengrenzlinie der Bemessungswerte. Die Momentengrenzlinie besteht somit aus bereichsweisen verschieden zusammengesetzten Funktionen. Somit ist diese keine „glatte Funktion“ und kann dementsprechend Knickstellen enthalten.<ref Name = "Springer"></ref> | ||
:::Wurden bei der Biegebemessung die Stützmomente aufgrund der Auflagersituation abgemindert (Momentenausrundung), so ist dies beim Erstellen der Momentengrenzlinie ebenfalls zu Berücksichtigen.<ref Name = "Stahlbeton for Beginners"></ref> | :::Wurden bei der Biegebemessung die Stützmomente aufgrund der Auflagersituation abgemindert (Momentenausrundung), so ist dies beim Erstellen der Momentengrenzlinie ebenfalls zu Berücksichtigen.<ref Name = "Stahlbeton for Beginners"></ref> | ||
| − | + | <br> | |
| − | :::[[Datei:Zugkraftdeckung 1.png|mini| | + | :::[[Datei:Zugkraftdeckung 1.png|mini|400px|none|Entwicklung der Momentengrenzlinie<ref Name = "Vorlesungsunterlagen"></ref> ]] |
| − | + | <br> | |
| − | :::[[Datei:Zugkraftdeckung 3.png|mini| | + | :::[[Datei:Zugkraftdeckung 3.png|mini|600px|none|Momentengrenzlinie mit ausgerundetem Stützmoment]] |
==Erstellen der Zugkraftlinie== | ==Erstellen der Zugkraftlinie== | ||
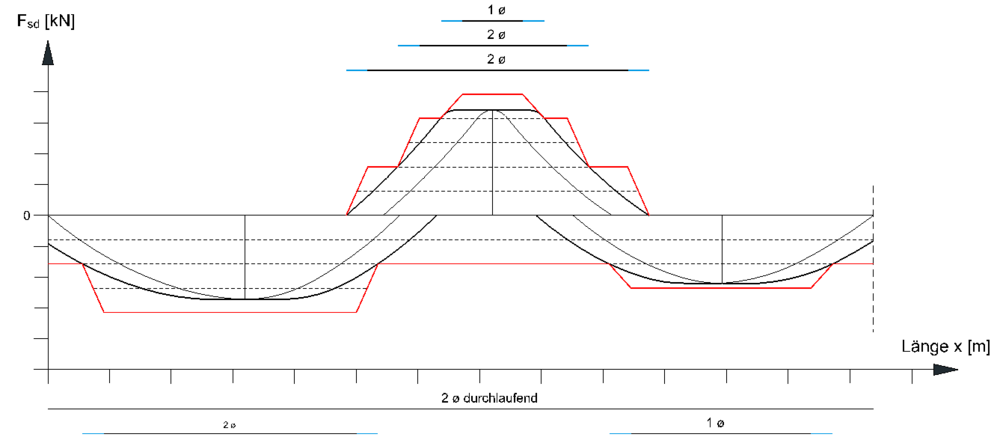
| − | Ziel: Näherungsweise den tatsächlichen Verlauf, der auf den Bewehrungsstahl einwirkenden | + | '''Ziel:''' Näherungsweise den tatsächlichen Verlauf, der auf den Bewehrungsstahl einwirkenden Zugkraft, im Zugkraftdiagramm darstellen. Hierbei ist stets die [[Zuggurtkraftdifferenz]] zu berücksichtigen. |
===Übersicht=== | ===Übersicht=== | ||
:*'''Ablauf zum Erstellen der Zugkraftlinie:''' | :*'''Ablauf zum Erstellen der Zugkraftlinie:''' | ||
| + | <br> | ||
::Grundlage: M<sub>Ed</sub> – Linie (Momentengrenzlinie) | ::Grundlage: M<sub>Ed</sub> – Linie (Momentengrenzlinie) | ||
:::↓ | :::↓ | ||
| − | ::M/z - Linie (Zugkraft F<sub>s</sub> aufgrund von Biegemomenten | + | ::M/z - Linie (Zugkraft F<sub>s</sub> aufgrund von Biegemomenten) |
:::↓ | :::↓ | ||
| − | :: | + | ::F<sub>sd</sub> – Linie (Zugkraft F<sub>s</sub> aufgrund von Biegemomenten und Querkraft) |
| − | + | <br> | |
:*'''Betrachtung vorab - innere Käfte:''' | :*'''Betrachtung vorab - innere Käfte:''' | ||
| − | ::Wird ein Stahlbetonbauteil auf Biegung beansprucht, so entstehen infolge des Biegemomentes Druck- und Zugspannungen im Bauteilquerschnitt. Die Druckspannung wird durch den Beton und die Zugspannung durch den Bewehrungsstahl aufgenommen. Aus den Spannungen resultieren die Betondruckkraft F<sub>cd</sub> und die Stahlzugkraft F<sub>sd</sub>, welche als innere Kräfte bezeichnet werden. Diese befinden sich im Gleichgewicht (F<sub>cd</sub> + F<sub>sd</sub> = 0). Aufgrund der Lage der inneren Kräfte im Bauteilquerschnitt ergibt sich zwischen diesen ein Abstand, welcher als Hebelarm der inneren Kräfte (z) bezeichnet wird.<ref Name = "Vorlesungsunterlagen">Bolle, G: Vorlesungsunterlagen Stahlbetonbau I, Hochschule Wismar, 2022 | + | [[Datei:Zugkraftdeckung 4.png|mini|200px|right|Darstellung der inneren Kräfte am Betrachtungsschnitt eines Stahlbetonbalken<ref Name = "Vorlesungsunterlagen"></ref> ]] |
| − | + | ::Wird ein Stahlbetonbauteil auf Biegung beansprucht, so entstehen infolge des Biegemomentes Druck- und Zugspannungen im Bauteilquerschnitt. Die Druckspannung wird durch den Beton und die Zugspannung durch den Bewehrungsstahl aufgenommen. Aus den Spannungen resultieren die Betondruckkraft F<sub>cd</sub> und die Stahlzugkraft F<sub>sd</sub>, welche als innere Kräfte bezeichnet werden. Diese befinden sich im Gleichgewicht (F<sub>cd</sub> + F<sub>sd</sub> = 0). Aufgrund der Lage der inneren Kräfte im Bauteilquerschnitt ergibt sich zwischen diesen ein Abstand, welcher als '''Hebelarm der inneren Kräfte (z)''' bezeichnet wird.<ref Name = "Vorlesungsunterlagen">Bolle, G: Vorlesungsunterlagen Stahlbetonbau I, Hochschule Wismar, 2022</ref> | |
| − | |||
| + | ::Mit dem Hebelarm der inneren Kräfte lässt sich über das einwirkende Biegemoment die Betondruckkraft F<sub>cd</sub> und die Stahlzugkraft F<sub>sd</sub> bestimmen.<ref Name = "Vorlesungsunterlagen"></ref> | ||
| + | <br> | ||
===M/z - Linie (Zugkraft aufgrund von Biegemomenten)=== | ===M/z - Linie (Zugkraft aufgrund von Biegemomenten)=== | ||
| − | Die M/z Linie lässt sich aus der Momentengrenzline bestimmen. Sie stellt die Stahlzugkraft F<sub>sd</sub> in Abhängigkeit vom einwirkenden Biegemoment in einem Längen-Kräfte-Diagramm dar. Der Verlauf der M/z Linie entspricht dem der Momentengrenzlinie, da Zugkraft und Moment direkt proportional zueinander sind?????. Bezogen auf das Diagramm ist hier prinzipiell lediglich die Einheit der Ordinate von kNm zu kN zu ändern. | + | Die M/z Linie lässt sich aus der Momentengrenzline bestimmen. Sie stellt die Stahlzugkraft F<sub>sd</sub> in Abhängigkeit vom einwirkenden Biegemoment in einem Längen-Kräfte-Diagramm dar. Der Verlauf der M/z Linie entspricht dem der Momentengrenzlinie, da Zugkraft und Moment direkt proportional zueinander sind?????. Bezogen auf das Diagramm ist hier prinzipiell lediglich die Einheit der Ordinate von kNm zu kN zu ändern. Bei einer zusätzlichen Belastung des Querschnittes durch eine Normalkraft ist diese zusätzlich rechnerisch zu berücksichtigen.<ref Name = "Vorlesungsunterlagen"></ref> |
| − | Bei einer zusätzlichen Belastung des Querschnittes durch eine Normalkraft ist diese rechnerisch zu berücksichtigen.<ref Name = "Vorlesungsunterlagen"></ref> | ||
Die Stahlzugkraft F<sub>s</sub> errechnet sich somit zu:<ref Name = "Vorlesungsunterlagen"></ref> | Die Stahlzugkraft F<sub>s</sub> errechnet sich somit zu:<ref Name = "Vorlesungsunterlagen"></ref> | ||
| Zeile 63: | Zeile 62: | ||
| M<sub>Ed</sub>... || Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie) | | M<sub>Ed</sub>... || Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie) | ||
|- | |- | ||
| − | | z... || Hebelarm der inneren Kräfte. Vereinfachend und auf der sicheren Seite liegend ist dieser zu 0,9 · d zu bestimmen (d = Statische Nutzhöhe). Eventuell kleinere Werte für z, aufgrund erheblicher Normalkräfte (z.B. aus Vorspannung) sind jedoch zu berücksichtigen. Prinzipiell kann z auch aus der Biegebemessung übernommen werden. Hierbei ist aber zu beachten, dass dieser nur für die Extremstellen bestimmt wird. Entlang das Bauteils können unter Umständen maßgebendere Werte vorliegen.<ref Name = "EC2"></ref> | + | | z... || Hebelarm der inneren Kräfte. Vereinfachend und auf der sicheren Seite liegend ist dieser zu 0,9 · d zu bestimmen (d = Statische Nutzhöhe). Eventuell kleinere Werte für z, aufgrund erheblicher Normalkräfte (z.B. aus Vorspannung) sind jedoch zu berücksichtigen. Prinzipiell kann z auch aus der Biegebemessung übernommen werden. Hierbei ist aber zu beachten, dass dieser dabei nur für die Extremstellen bestimmt wird. Entlang das Bauteils können unter Umständen maßgebendere Werte vorliegen.<ref Name = "EC2"></ref> |
|- | |- | ||
| − | | N<sub>Ed</sub>... || Bemessungswert | + | | N<sub>Ed</sub>... || Bemessungswert der einwirkenden Normalkraft (N<sub>Ed</sub> als Druckkraft negativ ansetzen) |
|} | |} | ||
| − | + | <br> | |
| + | [[Datei:Zugkraftdeckung 5.png|mini|600px|none|M<sub>Ed</sub>/z – Linie ]] | ||
===F<sub>sd</sub> – Linie (Zugkraft aufgrund von Biegemomenten und Querkraft)=== | ===F<sub>sd</sub> – Linie (Zugkraft aufgrund von Biegemomenten und Querkraft)=== | ||
Um den tatsächlichen Verlauf der Stahlzugkraft aufgrund von Biegemoment und Querkraft im Zugkraftdiagramm darzustellen, ist die [[Zuggurtkraftdifferenz]] zu berücksichtigen. Hierfür ist die M/z – Linie entsprechend anzupassen.<ref Name = "Springer"></ref> | Um den tatsächlichen Verlauf der Stahlzugkraft aufgrund von Biegemoment und Querkraft im Zugkraftdiagramm darzustellen, ist die [[Zuggurtkraftdifferenz]] zu berücksichtigen. Hierfür ist die M/z – Linie entsprechend anzupassen.<ref Name = "Springer"></ref> | ||
| − | Berücksichtigt werden kann die | + | Berücksichtigt werden kann die Zuggurtkraftdifferenz nach zwei Varianten: |
====Variante 1 - Rechnerisches Ermitteln==== | ====Variante 1 - Rechnerisches Ermitteln==== | ||
[[Datei:Zugkraftdeckung 6.png|mini|350px|right|Detailbetrachtung am Zugkraftdiagramm – Differenzkraft rechnerisch ermittelt]] | [[Datei:Zugkraftdeckung 6.png|mini|350px|right|Detailbetrachtung am Zugkraftdiagramm – Differenzkraft rechnerisch ermittelt]] | ||
| − | Entsprechend des Querkraft- und Momentenverlaufes kann die | + | Entsprechend des Querkraft- und Momentenverlaufes kann die Zuggurtkraftdifferenz ΔF<sub>s</sub> rechnerisch ermittelt werden. Hierfür muss nicht nur die Momentengrenzlinie, sondern auch der vollständige Querkraftverlauf bekannt sein. |
| − | Die | + | Die Zuggurtkraftdifferenz ΔF<sub>s</sub> ergibt sich zu:<ref Name = "Vorlesungsunterlagen"></ref> |
:<math>\Delta F_\mathrm{s} = V_\mathrm{Ed}\cdot\cfrac{1}{2}\cdot(cot \theta-cot \alpha)</math> | :<math>\Delta F_\mathrm{s} = V_\mathrm{Ed}\cdot\cfrac{1}{2}\cdot(cot \theta-cot \alpha)</math> | ||
| Zeile 93: | Zeile 93: | ||
| M<sub>Ed</sub>... || Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie) | | M<sub>Ed</sub>... || Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie) | ||
|} | |} | ||
| − | + | <br> | |
====Variante 2 - Konstruktive Berücksichtigung über das [[Versatzmaß]] a<sub>l</sub>==== | ====Variante 2 - Konstruktive Berücksichtigung über das [[Versatzmaß]] a<sub>l</sub>==== | ||
[[Datei:Zugkraftdeckung 7.png|mini|350px|right|Detailbetrachtung am Zugkraftdiagramm – Differenzkraft über Versatzmaß berücksichtigt]] | [[Datei:Zugkraftdeckung 7.png|mini|350px|right|Detailbetrachtung am Zugkraftdiagramm – Differenzkraft über Versatzmaß berücksichtigt]] | ||
| − | Hierbei wird die M/z – Linie horizontal um das [[Versatzmaß]] a<sub>l</sub> parallelverschoben. | + | Hierbei wird die M/z – Linie an der Extremstelle geteilt und jeweils horizontal um das [[Versatzmaß]] a<sub>l</sub> parallelverschoben. Der Kräftezuwachs aus der [[Zuggurtkraftdifferenz]] ergibt sich somit automatisch über die Geometrie. |
| − | Bei Bauteilen ohne Querkraftbewehrung ist dies generell die | + | Bei Bauteilen ohne Querkraftbewehrung ist dies generell die einzig mögliche Variante. <ref Name = "Teubner"></ref> |
| − | |||
::'''Vorteile dieser Variante''': | ::'''Vorteile dieser Variante''': | ||
| − | ::Das Bestimmen des [[Versatzmaß]] al bietet beim grafischen Durchführen der Zugkraftdeckung den entscheidenden Vorteil, dass die | + | ::Das Bestimmen des [[Versatzmaß]] al bietet beim grafischen Durchführen der Zugkraftdeckung den entscheidenden Vorteil, dass die M/z - Linie lediglich abschnittsweise um diesen Wert horizontal verschoben werden muss. Andernfalls müsste aufwendig stellenweise je nach einwirkendem Moment und Querkraft die Differenzkraft errechnet und vertikal angetragen werden. |
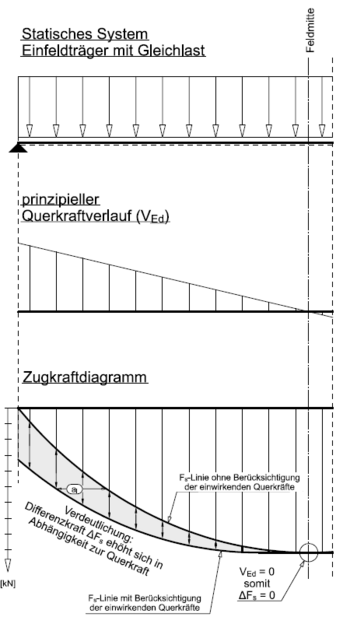
::Verdeutlicht wird dies am nachfolgenden Beispiel eines Einfeldträgers mit Gleichlast (siehe Grafik). Aufgrund der Belastungsart ergibt sich ein linearer Querkraftverlauf und ein parabolischer Momentenverlauf. Somit verläuft die Zugkraftlinie aus der Biegetheorie automatisch ebenfalls parabolisch. Aufgrund des linearen Querkraftverlaufes steigt die Größe der Differenzkraft kontinuierlich zum Auflager hin an. Durch das geometrische Verschieben der Zugkraftlinie um das [[Versatzmaß]] wird der kontinuierliche Zugkraftzuwachs konstruktiv berücksichtigt und somit näherungsweise erfasst. Das aufwendige rechnerische Ermitteln des Zugkraftzuwachses entfällt somit. | ::Verdeutlicht wird dies am nachfolgenden Beispiel eines Einfeldträgers mit Gleichlast (siehe Grafik). Aufgrund der Belastungsart ergibt sich ein linearer Querkraftverlauf und ein parabolischer Momentenverlauf. Somit verläuft die Zugkraftlinie aus der Biegetheorie automatisch ebenfalls parabolisch. Aufgrund des linearen Querkraftverlaufes steigt die Größe der Differenzkraft kontinuierlich zum Auflager hin an. Durch das geometrische Verschieben der Zugkraftlinie um das [[Versatzmaß]] wird der kontinuierliche Zugkraftzuwachs konstruktiv berücksichtigt und somit näherungsweise erfasst. Das aufwendige rechnerische Ermitteln des Zugkraftzuwachses entfällt somit. | ||
::[[Datei:Zugkraftdeckung 8.png|mini|350px|none|Zusammenhang Querkraft-Zuggurtkraftdifferenz]] | ::[[Datei:Zugkraftdeckung 8.png|mini|350px|none|Zusammenhang Querkraft-Zuggurtkraftdifferenz]] | ||
| − | + | <br> | |
====Hinweise==== | ====Hinweise==== | ||
| − | Beide Varianten führen | + | Beide Varianten führen schlussendlich zum nahezu gleichen Ergebnis: → Eine Zugkraftlinie, welche näherungsweise die tatsächlich einwirkende Stahlzugkraft darstellt. |
| − | Eine Zugkraftlinie, welche näherungsweise die tatsächlich einwirkende Stahlzugkraft darstellt. | + | <br> |
| − | + | [[Datei:Zugkraftdeckung 9.png|mini|800px|none|Endgültige Zugkraftlinie (Zuggurtkraftdifferenz berücksichtig über Versatzmaß a<sub>l</sub>)]] | |
| − | [[Datei:Zugkraftdeckung 9.png|mini| | + | <br> |
| + | Das [[Versatzmaß]] a<sub>l</sub> ist in den meisten Fällen für die jeweils einzelnen Abschnitte am statischen System aufgrund teilweise unterschiedlicher statischer Nutzhöhen und somit veränderter Hebelarme der inneren Kräfte jeweils gesondert zu bestimmen. | ||
| − | |||
Die einwirkende Stahlzugkraft an der Stelle des extremen Momentes (M<sub>Ed</sub> max) ist generell als oberer Grenzwert anzusehen. Die umliegenden Bereiche sind somit nicht höher als der Grenzwert anzusetzen. Auch wenn das Berücksichtigen der Zugkraftdifferenz offensichtlich zu höheren Werten führen würde. Deutlich wird dies am Verlauf der Zugkraftlinie an den Extremstellen. Dort ist ein Zeitweise konstanter Verlauf mit der Länge 2 · a<sub>l</sub> erkennbar. Der Grenzwert wird dabei nicht überschritten.<ref Name = "EC2"></ref> | Die einwirkende Stahlzugkraft an der Stelle des extremen Momentes (M<sub>Ed</sub> max) ist generell als oberer Grenzwert anzusehen. Die umliegenden Bereiche sind somit nicht höher als der Grenzwert anzusetzen. Auch wenn das Berücksichtigen der Zugkraftdifferenz offensichtlich zu höheren Werten führen würde. Deutlich wird dies am Verlauf der Zugkraftlinie an den Extremstellen. Dort ist ein Zeitweise konstanter Verlauf mit der Länge 2 · a<sub>l</sub> erkennbar. Der Grenzwert wird dabei nicht überschritten.<ref Name = "EC2"></ref> | ||
Version vom 25. März 2024, 23:45 Uhr
Unter Zugkraftdeckung versteht man die Ermittlung der statisch notwendigen Menge der Biegezugbewehrung, bezogen auf die Längsachse des Biegebauteils. Man spricht dabei vom Anpassen der Biegezugbewehrung an den Zugkraftverlauf. Durch den Nachweis der Zugkraftdeckung wird sichergestellt, dass in jedem Querschnitt die auftretende Zuggurtkraft durch die vorhandene Bewehrung aufgenommen werden kann.[1]
Problemstellung und Einführung in die Thematik
Wird die Menge der Biegezugbewehrung für ein biegebeanspruchtes Stahlbetonbauteil ermittelt, so ist hierfür an erster Stelle, das maximal wirkende Biegemoment maßgebend. Dieses befindet sich in der Regel, je nach statischem System, in Feldmitte (Feldmoment), im Bereich von Zwischenauflagern (Stützmoment) oder auch im Anschnitt eines Kragarms. Die weiteren Abschnitte entlang der Bauteilachse, in denen geringere Biegemomente wirken, sind für die reine Biegebemessung somit nicht relevant und bleiben hierbei unberücksichtigt. Eine Variante der Bewehrungsführung wäre nun, die für das maximale Biegemoment ermittelte Bewehrungsmenge, über die gesamte Bauteillänge unverändert in der entsprechenden Bauteilebene anzuordnen. Diese Variante der Bewehrungsführung kommt in der Praxis auch durchaus in vielen Fällen zur Anwendung. Der entscheidende Nachteil hierbei ist jedoch, dass je nach Bauteilgröße eine teilweise wesentlich höhere Bewehrungsstahlmenge verbaut wird, als tatsächlich nötig wäre. Grund dafür ist die Tatsache, dass auf der gesamten Bauteillänge eine einheitliche Bewehrungsmenge angeordnet wird, welche auf das maximale Biegemoment abgestimmt ist. Betrachtet man jedoch den Momentenverlauf im Bauteil, so fällt dieser ja nach dem maximalen Moment mit einem linearen oder parabolischen Verlauf ab. Daraus lässt sich herleiten, dass die weniger stark beanspruchten Bauteilbereiche somit auch weniger Bewehrungsstahl benötigen. Hierbei kann das Verfahren der Zugkraftdeckung angewendet werden. Man spricht dabei vom Anpassen der Biegezugbewehrung an den Zugkraftverlauf. Eine Ähnliche Vorgehensweise findet man im Stahlbetonbau auch bei der Querkraftbemessung. Hier wird über die Querkraftdeckung die Querkraftbewehrung an den Verlauf der Querkraft angepasst.[1][2][3]
Ziel ist es vereinfachend gesagt, den Materialeinsatz in Form von Bewehrungsstahl an die vom Momentenverlauf abhängige Stahlzugkraft anzupassen. Ähnliche Beispiele sind im Stahl- oder Holzbau zu finden. Zum Beispiel beim sogenannten „Fischbauchträger“. Dort wird die Bauteilkontur entsprechend des Momentenverlaufes gestaltet.
Normung und Anwendung
Geregelt ist das Verfahren der Zugkraftdeckung im Eurocode 2 (DIN EN 1992-1-1 mit Nationalem Anhang) im Kapitel 9 (Konstruktionsregeln)[4] . Im Unterschied zur DIN 1045-1 darf mit der Einführung des Eurocodes nun auch als zusätzliche Variante ein linearer Kraftverlauf entlang der Verankerungslänge bei der Abdeckung der Zugkraftlinie durch gestaffelte Bewehrung berücksichtigt werden (siehe Variantenvergleich Zugkraftdeckungslinien).[4]
Anwendung findet das Verfahren der Zugkraftdeckung bei verschiedensten biegebeanspruchten Stahlbetonbauteilen. Insbesondere Balken, Platten, Plattenbalken und Stützen. Also Bauteile, bei welchen es aus wirtschaftlichen- oder platztechnischen Gründen sinnvoll ist, die Biegezugbewehrung an den Zugkraftverlauf anzupassen und entsprechend abzustufen. Die hieraus resultierenden Vorteile sind die Einsparung von Bewehrungsstahl und damit verknüpft auch ein Platzgewinn für anderweitige Bewehrungselemente in Bauteilen mit einem hohen Bewehrungsgrad.[1]
Der Nachweis der Zugkraftdeckung ist zwingend in jedem Falle im Anschluss an die Biegebemessung zu vollziehen. Hiermit wird sichergestellt und nachgewiesen, dass die in jedem Querschnitt auftretende Zuggurtkraft durch die vorhandene Bewehrung aufgenommen wird.[2]
Vorgehensweise bei der Zugkraftdeckung
Grundvoraussetzungen für das Anwenden der Zugkraftdeckung
Im Allgemeinen genügt beim Nachweis der Zugkraftdeckung das Betrachten des Grenzzustandes der Tragfähigkeit. Werden jedoch Biegemomente mehr als 15% bei Linear-elastischer Berechnung umgelagert oder es kommt durch Verfahren der Schnittgrößenermittlung mit der Plastizitätstheorie/Nichtlineare Verfahren zu erheblichen Verschiebungen der Momentennullpunkte zwischen GZG und GZT, so ist der Nachweis ebenfalls für den Grenzzustand der Gebrauchstauglichkeit zu führen.[4] Im folgenden wird von einer Schnittgrößenermittlung nach dem linear-elastischen Verfahren ohne Momentenumlagerung ausgegangen.
- Bewehrungsmengen für die maßgebenden Biegemomente
- Die Anzahl und Durchmesser der Bewehrungsstäbe (Biegezugbewehrung) für die maßgebenden Biegemomente entsprechend der Biegebemessung müssen für die Zugkraftdeckung bekannt sein.
- Abgeschlossene Querkraftbemessung
- Der Querkraftverlauf und die Druckstrebenneigungswinkel aus der Querkraftbemessung sind für die Zugkraftdeckung erforderlich.
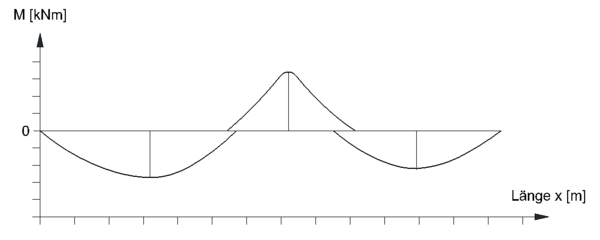
- Momentengrenzlinie (Umhüllende)
- Anders als bei der reinen Biegebemessung sind bei der Zugkraftdeckung nicht nur die Einzelwerte der Momente an den maßgebenden Extremstellen relevant, sondern die gesamte Momentengrenzlinie.
- Erläuterung - Momentengrenzlinie:
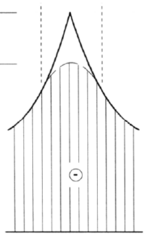
- Die maßgebenden Biegemomente an einem statischen System resultieren aufgrund unterschiedlicher Laststellungen (siehe Grafik). Das maßgebende Feldmoment an einem Durchlaufträger entsteht z.B. aufgrund einer anderen Laststellung als für das maßgebende Stützmoment. Legt man die Momentenlinien der jeweiligen Lastfälle für die maßgebenden Bemessungsmomente übereinander und betrachtet die umhüllende Außenkontur, so erhält man die Momentengrenzlinie der Bemessungswerte. Die Momentengrenzlinie besteht somit aus bereichsweisen verschieden zusammengesetzten Funktionen. Somit ist diese keine „glatte Funktion“ und kann dementsprechend Knickstellen enthalten.[2]
- Wurden bei der Biegebemessung die Stützmomente aufgrund der Auflagersituation abgemindert (Momentenausrundung), so ist dies beim Erstellen der Momentengrenzlinie ebenfalls zu Berücksichtigen.[1]
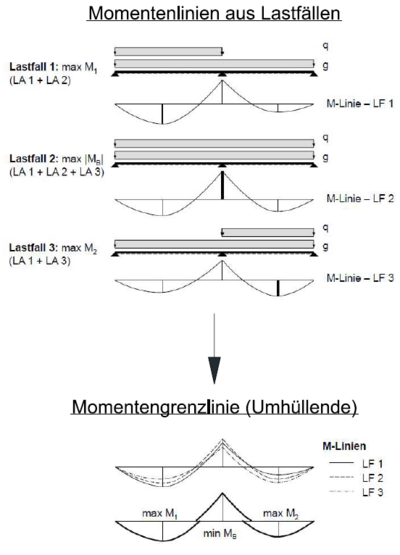 Entwicklung der Momentengrenzlinie[5]
Entwicklung der Momentengrenzlinie[5]
Erstellen der Zugkraftlinie
Ziel: Näherungsweise den tatsächlichen Verlauf, der auf den Bewehrungsstahl einwirkenden Zugkraft, im Zugkraftdiagramm darstellen. Hierbei ist stets die Zuggurtkraftdifferenz zu berücksichtigen.
Übersicht
- Ablauf zum Erstellen der Zugkraftlinie:
- Grundlage: MEd – Linie (Momentengrenzlinie)
- ↓
- M/z - Linie (Zugkraft Fs aufgrund von Biegemomenten)
- ↓
- Fsd – Linie (Zugkraft Fs aufgrund von Biegemomenten und Querkraft)
- Grundlage: MEd – Linie (Momentengrenzlinie)
- Betrachtung vorab - innere Käfte:
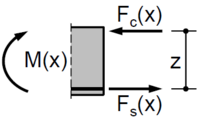
- Wird ein Stahlbetonbauteil auf Biegung beansprucht, so entstehen infolge des Biegemomentes Druck- und Zugspannungen im Bauteilquerschnitt. Die Druckspannung wird durch den Beton und die Zugspannung durch den Bewehrungsstahl aufgenommen. Aus den Spannungen resultieren die Betondruckkraft Fcd und die Stahlzugkraft Fsd, welche als innere Kräfte bezeichnet werden. Diese befinden sich im Gleichgewicht (Fcd + Fsd = 0). Aufgrund der Lage der inneren Kräfte im Bauteilquerschnitt ergibt sich zwischen diesen ein Abstand, welcher als Hebelarm der inneren Kräfte (z) bezeichnet wird.[5]
- Mit dem Hebelarm der inneren Kräfte lässt sich über das einwirkende Biegemoment die Betondruckkraft Fcd und die Stahlzugkraft Fsd bestimmen.[5]
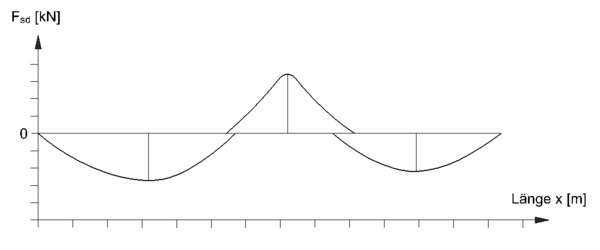
M/z - Linie (Zugkraft aufgrund von Biegemomenten)
Die M/z Linie lässt sich aus der Momentengrenzline bestimmen. Sie stellt die Stahlzugkraft Fsd in Abhängigkeit vom einwirkenden Biegemoment in einem Längen-Kräfte-Diagramm dar. Der Verlauf der M/z Linie entspricht dem der Momentengrenzlinie, da Zugkraft und Moment direkt proportional zueinander sind?????. Bezogen auf das Diagramm ist hier prinzipiell lediglich die Einheit der Ordinate von kNm zu kN zu ändern. Bei einer zusätzlichen Belastung des Querschnittes durch eine Normalkraft ist diese zusätzlich rechnerisch zu berücksichtigen.[5]
Die Stahlzugkraft Fs errechnet sich somit zu:[5]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{s}=\cfrac{M_\mathrm{Ed}}{z}+N_\mathrm{Ed}}
MEd... Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie) z... Hebelarm der inneren Kräfte. Vereinfachend und auf der sicheren Seite liegend ist dieser zu 0,9 · d zu bestimmen (d = Statische Nutzhöhe). Eventuell kleinere Werte für z, aufgrund erheblicher Normalkräfte (z.B. aus Vorspannung) sind jedoch zu berücksichtigen. Prinzipiell kann z auch aus der Biegebemessung übernommen werden. Hierbei ist aber zu beachten, dass dieser dabei nur für die Extremstellen bestimmt wird. Entlang das Bauteils können unter Umständen maßgebendere Werte vorliegen.[4] NEd... Bemessungswert der einwirkenden Normalkraft (NEd als Druckkraft negativ ansetzen)
Fsd – Linie (Zugkraft aufgrund von Biegemomenten und Querkraft)
Um den tatsächlichen Verlauf der Stahlzugkraft aufgrund von Biegemoment und Querkraft im Zugkraftdiagramm darzustellen, ist die Zuggurtkraftdifferenz zu berücksichtigen. Hierfür ist die M/z – Linie entsprechend anzupassen.[2]
Berücksichtigt werden kann die Zuggurtkraftdifferenz nach zwei Varianten:
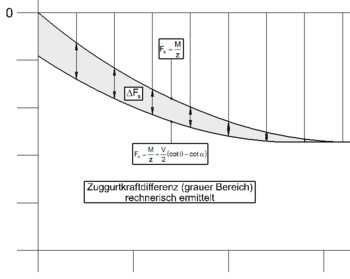
Variante 1 - Rechnerisches Ermitteln
Entsprechend des Querkraft- und Momentenverlaufes kann die Zuggurtkraftdifferenz ΔFs rechnerisch ermittelt werden. Hierfür muss nicht nur die Momentengrenzlinie, sondern auch der vollständige Querkraftverlauf bekannt sein.
Die Zuggurtkraftdifferenz ΔFs ergibt sich zu:[5]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_\mathrm{s} = V_\mathrm{Ed}\cdot\cfrac{1}{2}\cdot(cot \theta-cot \alpha)}
Die Gesamtkraft Fs ergibt sich somit zu:[5]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{s} = \cfrac{M_\mathrm{Ed}}{z}+V_\mathrm{Ed}\cdot\cfrac{1}{2}\cdot(cot \theta-cot \alpha)}
VEd... Bemessungswert der einwirkenden Querkraft cot θ... Druckstrebenneigungswinkel cot α... Neigungswinkel der Bügelbewehrung z... Hebelarm der inneren Kräfte MEd... Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie)
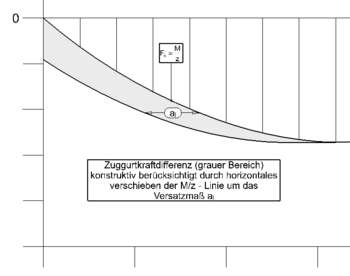
Variante 2 - Konstruktive Berücksichtigung über das Versatzmaß al
Hierbei wird die M/z – Linie an der Extremstelle geteilt und jeweils horizontal um das Versatzmaß al parallelverschoben. Der Kräftezuwachs aus der Zuggurtkraftdifferenz ergibt sich somit automatisch über die Geometrie. Bei Bauteilen ohne Querkraftbewehrung ist dies generell die einzig mögliche Variante. [3]
- Vorteile dieser Variante:
- Das Bestimmen des Versatzmaß al bietet beim grafischen Durchführen der Zugkraftdeckung den entscheidenden Vorteil, dass die M/z - Linie lediglich abschnittsweise um diesen Wert horizontal verschoben werden muss. Andernfalls müsste aufwendig stellenweise je nach einwirkendem Moment und Querkraft die Differenzkraft errechnet und vertikal angetragen werden.
- Verdeutlicht wird dies am nachfolgenden Beispiel eines Einfeldträgers mit Gleichlast (siehe Grafik). Aufgrund der Belastungsart ergibt sich ein linearer Querkraftverlauf und ein parabolischer Momentenverlauf. Somit verläuft die Zugkraftlinie aus der Biegetheorie automatisch ebenfalls parabolisch. Aufgrund des linearen Querkraftverlaufes steigt die Größe der Differenzkraft kontinuierlich zum Auflager hin an. Durch das geometrische Verschieben der Zugkraftlinie um das Versatzmaß wird der kontinuierliche Zugkraftzuwachs konstruktiv berücksichtigt und somit näherungsweise erfasst. Das aufwendige rechnerische Ermitteln des Zugkraftzuwachses entfällt somit.
Hinweise
Beide Varianten führen schlussendlich zum nahezu gleichen Ergebnis: → Eine Zugkraftlinie, welche näherungsweise die tatsächlich einwirkende Stahlzugkraft darstellt.
Das Versatzmaß al ist in den meisten Fällen für die jeweils einzelnen Abschnitte am statischen System aufgrund teilweise unterschiedlicher statischer Nutzhöhen und somit veränderter Hebelarme der inneren Kräfte jeweils gesondert zu bestimmen.
Die einwirkende Stahlzugkraft an der Stelle des extremen Momentes (MEd max) ist generell als oberer Grenzwert anzusehen. Die umliegenden Bereiche sind somit nicht höher als der Grenzwert anzusetzen. Auch wenn das Berücksichtigen der Zugkraftdifferenz offensichtlich zu höheren Werten führen würde. Deutlich wird dies am Verlauf der Zugkraftlinie an den Extremstellen. Dort ist ein Zeitweise konstanter Verlauf mit der Länge 2 · al erkennbar. Der Grenzwert wird dabei nicht überschritten.[4]
Bewehrungshorizonte
Aus der bereits vollzogenen Biegebemessung sind Durchmesser und Anzahl der Bewehrungsstäbe als Biegezugbewehrung bekannt. Jeder einzelne Stab kann aufgrund seiner Querschnittsfläche und der Stahlfestigkeit eine entsprechende Zugkraft F⌀ aufnehmen.[5]
Die pro Bewehrungsstahl aufnehmbare Zugkraft F⌀ errechnet sich zu:[5]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{\varnothing_{}} = A_\mathrm{s\varnothing_{}}\cdot f_\mathrm{yd}}
As⌀... Querschnittsfläche des Bewehrungsstahls fyd... Bemessungswert der Stahlstreckgrenze
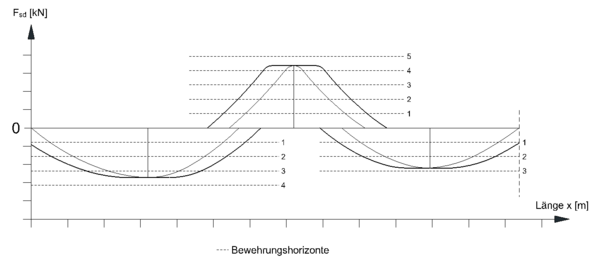
Die errechnete Zugkraft pro Bewehrungsstahl lässt sich im Zugkraftdiagramm über einen sogenannten Bewehrungshorizont (horizontale Hilfslinie) eintragen. Mit steigender Anzahl der Bewehrungsstähle kommen weitere Horizonte mit untereinander gleichem Abstand dazu. Ist dementsprechend die volle Anzahl der Bewehrungsstähle eingetragen lässt sich die Bewehrungsmenge aus der Biegebemessung mit der laut Zugkraftdiagramm erforderlichen Menge vergleichen. Die erforderliche Zugkraft muss von der Biegezugbewehrung abgedeckt werden. Je nach Bewehrungsdurchmesser und Stabanzahl können sich die Bewehrungshorizonte pro Bemessungsabschnitt am Statischen System unterscheiden.[1]
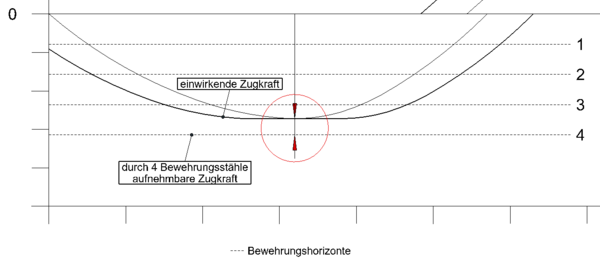
Betrachtung am Zugkraftdiagramm in Feld 1: aufnehmbare Zugkraft muss größer oder gleich der einwirkenden Zugkraft sein. Hierdurch lässt sich kontrollieren ob die gewählte Biegezugbewehrung korrekt gewählt wurde. Geringe Unterschreitungen können jedoch akzeptiert werden. Zurückzuführen ist dies auf den Hebelarm der inneren Kräfte (z). Die Biegebemessung und damit die Bewehrungswahl erfolgt mit dem exakten Wert für z. Die Zugkraftlinie hingegen wird auf der sicheren Seite liegend vereinfacht mit z = 0,9 · d bestimmt. Hierdurch wird im Zugkraftdiagramm eine teilweise etwas höhere Stahlzugkraft dargestellt, als tatsächlich auftreten wird.
Zugkraftdeckungslinie (Abstufen der Biegezugbewehrung)
Übersicht
Ziel des Abstufens ist es, die Biegezugbewehrung näherungsweise an den Zugkraftverlauf anzupassen. Man spricht dabei vom Staffeln der Bewehrung. Durch das Abstufen lassen sich die Längen der einzelnen Bewehrungsstähle festlegen, denn wie anfangs erwähnt, müssen nicht alle Stäbe bis ins Auflager geführt werden, sondern können teilweise schon vorher enden. Es bleibt freigestellt ob jeder Stahl einzeln Abgestuft wird oder mehrere Stäbe die gleiche Länge erhalten. Ergebnis ist die Zugkraftdeckungslinie. An jeder Stelle des Bauteils muss so viel Bewehrung angeordnet sein, das es nicht zum einschneiden der Zugkraftlinie durch die Zugkraftdeckungslinie kommt.[2]
Endet ein Bewehrungsstahl z.B. wie bei der Zugkraftdeckung durch Abstufung im Verlauf des Bauteils, so ist dieser dort noch zu verankern. Gängig ist es hierbei, das gerade Stabende unter Berücksichtigung seiner Verankerungslänge entsprechend enden zu lassen. Somit ist beim Abstufen von Bewehrungsstählen entsprechend der Zugkraftdeckungslinie, zusätzlich immer das Maß der Verankerungslänge in Bezug auf die Gesamtlänge eines Stabes zu Berücksichtigen. Eine weitere Form der Verankerung abgestufter Bewehrungsstähle sind unter anderem sogenannte „Schrägaufbiegungen“ (siehe Rückblick - Zugkraftdeckung in der Vergangenheit. [5]
Konstruktive Regeln
In Verbindung mit dem Abstufen von Bewehrungsstählen sind grundsätzliche Regeln zur Bewehrungsführung zu beachten.
- Verankerung am Endauflager:
- Mindestens 25% der Feldbewehrung sind bis zum Endauflager zu führen und dort zu verankern (bei Platten 50%). Als Verankerungsbeginn zählt die Innenkante des Auflagers. Die Bewehrung ist jedoch stets mindestens über die rechnerische Auflagerlinie zu führen.[6]
- Verankerung am Zwischenauflager:
- Mindestens 25% der Feldbewehrung sind über das Zwischenauflager zu führen. Die Mindestverankerungslänge ab Auflagerrand muss mindestens 6· dem Stabdurchmesser entsprechen. Zur Aufnahme positiver Momente infolge außergewöhnlicher Beanspruchungen (Auflagersetzungen, Explosion u. a.) sollte die Bewehrung durchlaufend ausgeführt werden (ggf. kraftschlüssig gestoßen).[6]
Weitere Hinweise zur Bewehrungsführung sind aus geeigneter Fachliteratur zu entnehmen z.B. [6].
Aufgrund der konstruktiven Regeln ist es somit nicht möglich jeden Bewehrungsstab Abzustufen und vor dem Auflager enden zu lassen. Ein gewisser Anteil ist in jedem Fall immer bis zum Auflager zu führen. Bei allen weiteren Stäben liegt es im eigenen Ermessen ob eine eher „feine“ oder „grobe“ Abstufung vollzogen wird.
Eine „feine“ Abstufung führt zwar zur Einsparung von Bewehrungsstahl, kann sich jedoch in Hinblick auf die Übersichtlichkeit im Bewehrungsplan und die spätere Bewehrungsmontage wiederum ungünstig auswirken. Denn die Anzahl der Bewehrungsstäbe mit unterschiedlicher Länge und somit auch die Anzahl an unterschiedlichen Positionen nimmt hierbei zu. Ein „gesundes Mittelmaß“ zwischen Materialeinsparung und Planungs-/Montageaufwand ist hierbei anzustreben.[5]
Erfassen der rechnerischen Endpunkte der Bewehrung
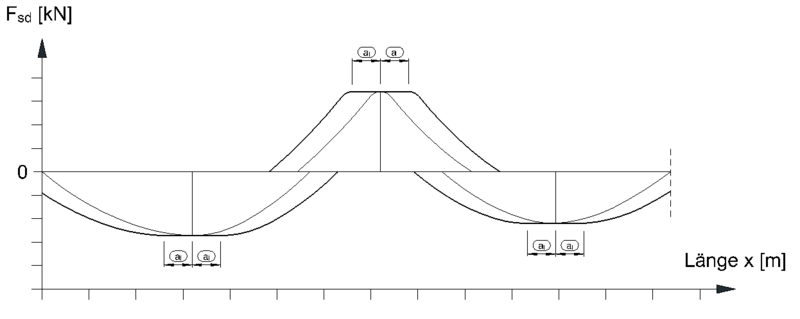
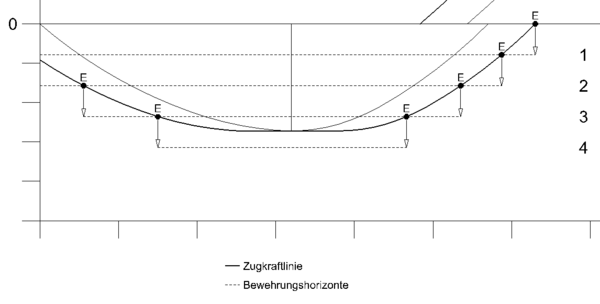
Ein Bewehrungsstahl kann enden/abgestuft werden, wenn dieser nicht mehr belastet wird, also dort wo keine Zugkraft mehr auf ihn einwirkt. Im Zugkraftdiagramm lässt sich der rechnerische Endpunkt (E) geometrisch erfassen. Der rechnerische Endpunkt eines Stabes befindet sich dort, wo sich die Zugkraftlinie mit dem Bewehrungshorizont des vorherigen Stabes schneidet. Beispielhaft darf Stab 4 dort enden, wo sich der Bewehrungshorizont von Stab 3 mit der Zugkraftlinie schneidet (siehe Grafik).
Der rechnerische Endpunkt bedeutet, das dort rein theoretisch abgestuft werden kann. Die Abstufung muss jedoch nicht zwangsläufig erfolgen, bzw. darf aus konstruktiven Gründen teilweise auch nicht überall vollzogen werden.
Varianten der Zugkraftdeckungslinie
Eine Zugkraftdeckungslinie lässt sich nach zwei Varianten erstellen. Die Varianten unterscheiden sich hinsichtlich des Ansatzes der Tragfähigkeit der Bewehrung in der Verankerungslänge der abgestuften Bewehrungsstähle (siehe Variantenvergleich Zugkraftdeckungslinien).[4]
Eine Zugkraftdeckungslinie richtet sich nach den rechnerischen Endpunkten und den Bewehrungshorizonten im Zugkraftdiagramm. Die konstruktiven Regeln der Bewehrungsführung sind zu Berücksichtigen. Ebenfalls muss bekannt sein, welche Anzahl an Stäben abgestuft werden sollen.
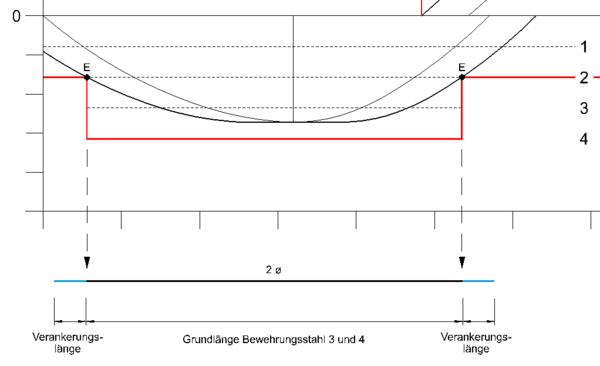
Variante a - Zugkraftdeckungslinie „Stufenfunktion“ (nach DIN 1045-1)
Bei der „Stufenfunktion“ handelt es sich um die „klassische“ Variante, welche auch die einzige Variante in der vor dem EC 2 geltenden DIN 1045-1 war. Die Tragfähigkeit der Bewehrung in der Verankerungslänge wird im Vergleich zu Variante b nicht angesetzt.[4]
- Beispielbetrachtung Feldbewehrung:
- Nach Biegebemessung sind 4 Bewehrungsstähle mit gleichem Durchmesser vorhanden. Hiervon sollen 2 Stäbe abgestuft werden. Die weiteren 2 Stäbe laufen vollständig von Auflager zu Auflager und werden nicht abgestuft um den Konstruktiven Regeln gerecht zu werden (mindestens 25% der Feldbewehrung ist bis ins Auflager zu führen).
Es lässt sich die Zugkraftdeckungslinie erstellen:
- Abgestuft wurden Stab 3 und 4 auf jeweils die gleiche Länge, bezogen auf die rechnerischen Endpunkten von Stab 3.
- Die erforderliche Länge der abgestuften Bewehrungsstähle wird nachfolgend veranschaulicht:
- Das Maß zwischen zwei Endpunkten (E) entspricht der Grundlänge des jeweiligen Bewehrungsstahls. Um die tatsächliche Stablänge zu erhalten, ist die jeweilige Verankerungslänge) der Grundlänge ab dem Endpunkt E hinzuzurechnen.
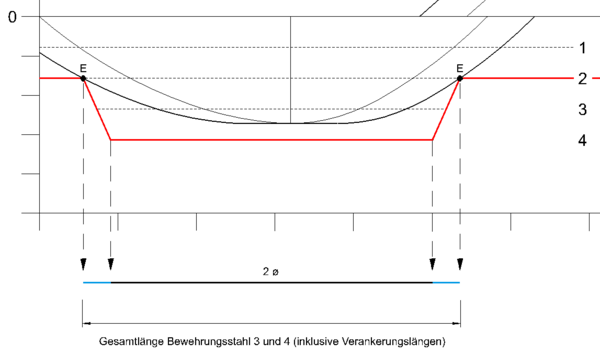
Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“ (nach EC 2)
Mit der Einführung des Eurocode 2 darf die Tragfähigkeit der Bewehrung in der Verankerungslänge in Ansatz gebracht werden. Hierdurch „schmiegt“ sich die Zugkraftdeckungslinie enger an die Zugkraftlinie an.[4]
- Beispielbetrachtung Feldbewehrung (gleichen Randbedingungen wie bei Variante a):
- Das Maß zwischen zwei Endpunkten (E) entspricht der Gesamtlänge des jeweiligen Bewehrungsstahls. Die Verankerungslängen sind hier drin schon enthalten. Abgestuft wurden Stab 3 und 4 auf jeweils die gleiche Länge, bezogen auf die rechnerischen Endpunkten von Stab 3.
Ergebnis der Zugkraftdeckung
Das Ergebnis der Zugkraftdeckung sind Länge und Position der abgestuften Bewehrungsstähle. Hierbei ist stets die Verankerungslänge zu berücksichtigen. Diese Parameter lassen sich direkt für die Stabstahlliste und den Bewehrungsplan verwenden. Verdeutlicht wird die Vorgehensweise der Zugkraftdeckung am Berechnungsbeispiel
Variantenvergleich Zugkraftdeckungslinien
Wie vorab exemplarisch dargestellt, lassen sich für das Erstellen einer Zugkraftdeckung grundsätzlich zwei Varianten in Betracht ziehen.
- Variante a - Zugkraftdeckungslinie „Stufenfunktion“
- ohne Ansatz der Tragfähigkeit der Bewehrung in der Verankerungslänge
- Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“
- mit Ansatz der Tragfähigkeit der Bewehrung in der Verankerungslänge
Ausgangspunkte der Varianten
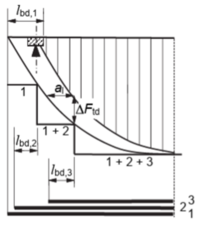
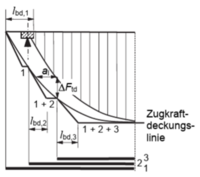
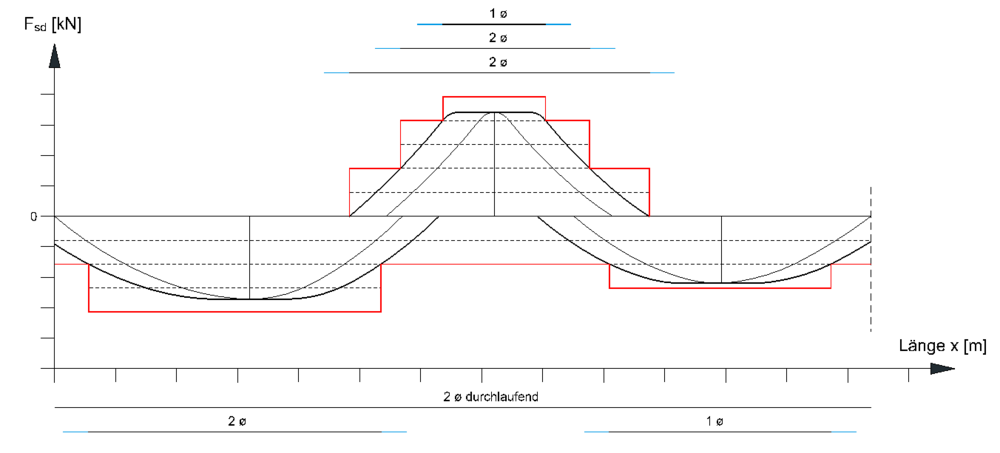
Betrachtet wird der rechnerische Endpunkt E eines abgestuften Bewehrungsstahls. Dort ist der Bewehrungsstahl unbelastet. Es wirkt an dieser Stelle somit keine Zugkraft. Nach Variante a ist der Stab ab dem rechnerischen Endpunkt mit seiner erforderlichen Verankerungslänge zu verankern. Aufgrund dessen kann der Bewehrungsstahl bereits ab dem Punkt E seinen vollständigen Bemessungswert der Zugkraft aufnehmen. Im Zugkraftdiagramm wird jedoch ersichtlich, dass ab dem Punkt E die Zugkraft im Bewehrungsstahl erst allmählich steigt. Betrachtet man nun den Verlauf der aufnehmbaren Zugkraft entlang der berechneten Verankerungslänge eines Stabes, so lässt sich feststellen dass diese am Stabende beginnend, linear bis zum Erreichen des Bemessungswertes ansteigt. Der lineare Verlauf ist hierbei auf die Verbundwirkung zwischen Stahl und Beton zurückzuführen. Dieser lineare Kräfteverlauf entlang der Verankerungslänge wird in Variante b bei der Zugkraftdeckungslinie berücksichtigt. Hierdurch lässt sich die Zugkraftdeckungslinie noch enger an die Zugkraftlinie anpassen und somit Material einsparen. Der Stab endet hierbei am rechnerischen Endpunkt und der lineare Kräfteverlauf in der Verankerungslänge wird in den Verlauf der Zugkraftdeckungslinie integriert.[4] [5]
 linearer Kraftanstieg innerhalb der Verankerungslänge[5]
linearer Kraftanstieg innerhalb der Verankerungslänge[5]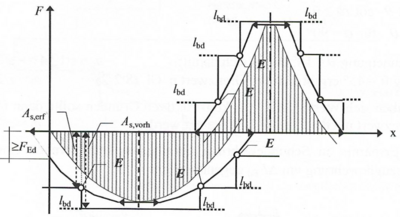 Variante-a Zugkraftdeckungslinie „Stufenfunktion“[2]
Variante-a Zugkraftdeckungslinie „Stufenfunktion“[2]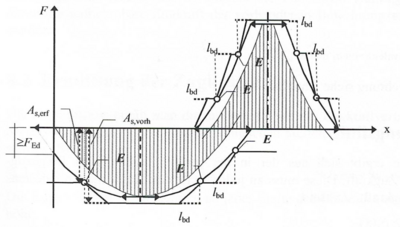 Variante-b Zugkraftdeckungslinie „anschmiegende Funktion[2]
Variante-b Zugkraftdeckungslinie „anschmiegende Funktion[2]
Beurteilung der Varianten
Aufgrund der Anrechnung der Tragfähigkeit der Bewehrung in der Verankerungslänge ergeben sich für Variante b generell kürzere Stablängen als für Variant a, was schlussendlich zu einer Materialersparnis führt. Die Materialeinsparung ist jedoch vergleichsweise gering. Positiv für Variante a spricht, das dort eine erhöhte Sicherheit gegen Ungenauigkeiten oder Abweichungen vorhanden ist. Denn durch eine eventuelle Abweichung der rechnerischen Zugkraftlinie von der tatsächlichen oder Verlegeungenauigkeiten, kann dies zu einer Verkürzung der Verankerungslänge oder Unterschreitung der Zugkraftdeckung führen.
Zitat Springer Massivbau: „Im Sinne nachhaltigen Bauens kann eine robustere Bauweise bei späteren Nutzungsänderungen eines Bauwerks hilfreich sein. Daher ist es häufig durchaus sinnvoll, die Bewehrungsführung anhand des vereinfachenden Stufenmodells zu ermitteln.“[2]
Hinweise zur Verankerung der Bewehrung
In Verbindung mit der Zugkraftdeckung ist die Verankerung der Bewehrungselemente nachzuweisen. Überall dort, wo ein Bewehrungsstahl endet, ist dieser auch entsprechend zu Verankern. Hierbei unterscheidet man hinsichtlich der Stelle des Endpunktes der Bewehrung in die Positionen Endauflager, Zwischenauflager und außerhalb von Auflagern.
Folglich wird lediglich der prinzipielle Berechnungsablauf am Standardfall der Verankerung eines geraden Stabendes erläutert. Konstruktive Regeln und weitere Details sind aus geeigneter Fachliteratur zu entnehmen z.B. [6].
Verankerung am Endauflager[6].
- Ermitteln der Randzugkraft FEd (Zugkraft am Endauflager)
VEd... Bemessungswert der einwirkenden Querkraft al... Versatzmaß aus Zugkraftdeckung z... Hebelarm der inneren Kräfte NEd... Bemessungswert der einwirkenden Normalkraft
- Ermitteln, des zur Aufnahme der Randzugkraft erforderlichen Bewehrungsquerschnitt
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_\mathrm{s,erf} =\cfrac{F_\mathrm{Ed}}{f_\mathrm{yd}}}
fyd... Bemessungswert der Stahlstreckgrenze
- Ermitteln der Stahlspannung
- Hierbei ist das Verhältnis aus erforderlicher und vorhandener Bewehrung zu bilden.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_\mathrm{sd} =\cfrac{A_\mathrm{s,erf}}{A_\mathrm{s,vorh}}\cdot f_\mathrm{yd}}
As,vorh... Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe
- Ermitteln der Verankerungslänge
- Mithilfe der zuvor bestimmten Stahlspannung lässt sich die Verankerungslänge über die dafür allgemeingültigen Formeln bestimmen
Verankerung am Zwischenauflager (Untere Bewehrung)[6].
Am Zwischenauflager ist die erforderliche Bewehrung mit mindestens der Länge von 6· dem Bewehrungsdurchmesser hinter den Auflagerrand zu führen.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{b,eq} =6\cdot\varnothing_{}\mathrm{s}}
Verankerung außerhalb von Auflagern[6].
Hiermit sind Bewehrungsstähle gemeint, welche abgestuft sind und nicht bis ins Auflager geführt wurden.
- Ermittlung der Stahlspannung am rechnerischen Endpunkt E
As,erf... Gesamtquerschnittsfläche der Stäbe, welche nicht Abgestuft wurden/ bzw. weiter durchlaufen As,vorh... Gesamtquerschnittsfläche aller vorhandenen Stäbe
- Ermitteln der Verankerungslänge
- Mithilfe der zuvor bestimmten Stahlspannung lässt sich die Verankerungslänge über die dafür allgemeingültigen Formeln bestimmen
Hinweise: Bei durchlaufender Bewehrung, welche nicht abgestuft wurde (z.B. untere Grundbewehrung) kann es aufgrund der großen Stablänge erforderlich werden, diesen zu stoßen. Die Art und Länge des Übergreifungsstoßes ist ebenfalls nachzuweisen.
An Endauflagern kann es unter Umständen aufgrund der begrenzten Platzverhältnisse notwendig sein eine gesonderte Verankerungsart zu wählen (z.B. Winkelhaken).
Rückblick - Zugkraftdeckung in der Vergangenheit
Die Zugkraftdeckung wird als solche bereits seit vielen Jahrzehnten praktiziert. Vergleichend betrachtet wurden verschiedene Lehr- und Handbücher für den Stahlbetonbau aus den frühen 1980er Jahren. Die Durchführung der Variante Zugkraftdeckungslinie „Stufenfunktion“, ist dort, abgesehen von anderen Begriffsbezeichnungen, nahezu identisch mit der heutigen Vorgehensweise. Als wesentlicher Unterschied ist jedoch erkennbar, das zu jener Zeit die sogenannten „Schrägaufbiegungen“ im Trend lagen. Hierbei wurden die abgestuften Bewehrungsstähle ab ihrem rechnerischen Endpunkt schräg aufgebogen und unter einem gewissen Winkel zum anderen Bauteilrand geführt und dort verankert. Somit dienten diese Stäbe gleichzeitig als Querkraftbewehrung. Die ansonsten geringe Anzahl an Bügelbewehrung galt damals oftmals lediglich als umhüllende Bewehrung zur Formgebung. Rückblickend betrachtet führte die Verwendung von Schrägstäben jedoch zu einigen Problemen. Darunter z.B. Betonabplatzungen an den Umlenkstellen der aufgebogenen Bewehrung oder aber auch Unstimmigkeiten bei der Verlegung, aufgrund der Vielzahl von unterschiedlichen Bewehrungspositionen. Heutzutage wird gefordert, das mindestens 50% der Querkraft über Bügelbewehrung abzutragen ist. Auch wenn das Bewehren mit Schrägstäben momentan eher selten zur Anwendung kommt, kann dies aufgrund der resultierenden Materialeinsparung jedoch grundsätzlich sehr wirtschaftlich sein. In Hinsicht auf die bevorstehenden Ressourcenknappheiten, kann es somit in Zukunft durchaus sinnvoll sein, die Bewehrung durch Schrägstäbe mit entsprechenden Optimierungen wieder mehr in den Fokus zu rücken. [7][2]
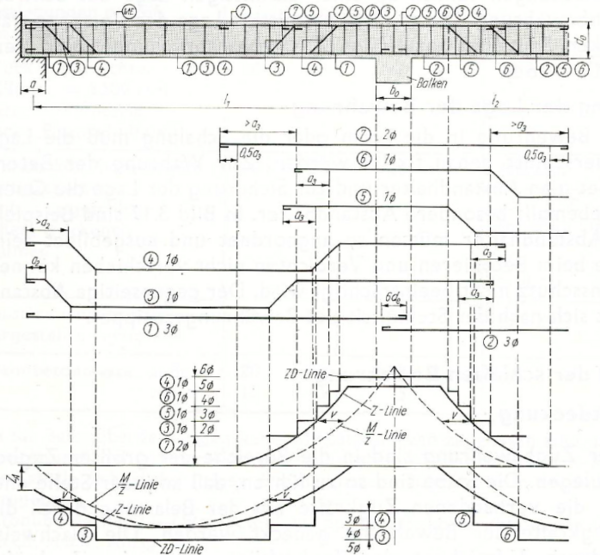 Zugkraftdeckungslinie und Bewehrungsführung (Lehrbuch aus dem Jahr 1979)[7]
Zugkraftdeckungslinie und Bewehrungsführung (Lehrbuch aus dem Jahr 1979)[7]
weitere Seiten zum Thema Zugkraftdeckung
Ouellen
- ↑ 1,0 1,1 1,2 1,3 1,4 Scheerer, S; Proske, D: Stahlbeton for Beginners, Grundlagen für die Bemessung und Konstruktion, 2. Auflage, Springer-Verlag, 2008
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 Bindseil, P.: Massivbau: Bemessung und Konstruktion im Stahlbetonbau mit Beispielen, 5. Auflage, Springer Vieweg Verlag, 2015
- ↑ 3,0 3,1 Gottfried C.O. Lohmeyer (Hrsg.): Stahlbetonbau, Bemessung - Konstruktion - Ausführung, 6. Auflage, Teubner Verlag
- ↑ 4,00 4,01 4,02 4,03 4,04 4,05 4,06 4,07 4,08 4,09 4,10 Eurocode 2: DIN EN 1992-1-1 mit Nationalem Anhang (2. Auflage):Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau - Konstruktionsregeln
- ↑ 5,00 5,01 5,02 5,03 5,04 5,05 5,06 5,07 5,08 5,09 5,10 5,11 5,12 5,13 5,14 Bolle, G: Vorlesungsunterlagen Stahlbetonbau I, Hochschule Wismar, 2022
- ↑ 6,0 6,1 6,2 6,3 6,4 6,5 6,6 Albert, A (Hrsg.): Bautabellen für Ingenieure, mit Berechnungshinweisen und Beispielen, 24. Auflage, Reguvis Verlag, 2020
- ↑ 7,0 7,1 Kaller, W; Raue, E; Böhme, H: Stahlbeton 1, Konstruktion und Berechnung, 3. Auflage, VEB Verlag für Bauwesen, 1979