Versatzmaß: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
| cot α... || Neigungswinkel der Querkraftbewehrung | | cot α... || Neigungswinkel der Querkraftbewehrung | ||
|- | |- | ||
| − | | z... || Hebelarm der inneren Kräfte kann aus der Biegebemessung übernommen werden oder näherungsweise zu z=0, | + | | z... || Der Hebelarm der inneren Kräfte kann aus der Biegebemessung übernommen werden oder näherungsweise zu z=0,9·d angesetzt werden. Eventuell können durch erhebliche Normalkräfte (z.B. aus Vorspannung) auch kleinere Werte maßgebend werden. |
|} | |} | ||
| − | + | ||
| + | Bei Bauteilen ohne Querkraftbewehrung gilt: | ||
| + | :<math>a_\mathrm{l} = d</math> | ||
| + | :::{| | ||
| + | | d... || statische Nutzhöhe | ||
| + | |} | ||
| + | |||
| + | Bei Druckstrebenneigungswinkeln θ > 45° gilt: | ||
| + | |||
| + | :<math>a_\mathrm{l} = \cfrac{z}{2}</math> | ||
| + | |||
a<sub>l</sub> ist gleichermaßen abhängig von α und θ | a<sub>l</sub> ist gleichermaßen abhängig von α und θ | ||
| Zeile 20: | Zeile 30: | ||
:für θ ↑ → a<sub>l</sub>↓ | :für θ ↑ → a<sub>l</sub>↓ | ||
:für α ↑ → a<sub>l</sub>↑ | :für α ↑ → a<sub>l</sub>↑ | ||
| + | <br> | ||
| − | + | :'''Besonderheit bei Plattenbalken:''' | |
:Wird bei Plattenbalken die Biegezugbewehrung aus dem Stegbereich ausgelagert (z.B. Stützbewehrung bei Zwischenauflagern), so ist das Versatzmaß a<sub>l</sub> um den Abstand x des am weitesten vom Stegrand ausgelagerten Bewehrungsstahl zu Vergrößern.<ref Name = "Vorlesungsunterlagen"></ref> | :Wird bei Plattenbalken die Biegezugbewehrung aus dem Stegbereich ausgelagert (z.B. Stützbewehrung bei Zwischenauflagern), so ist das Versatzmaß a<sub>l</sub> um den Abstand x des am weitesten vom Stegrand ausgelagerten Bewehrungsstahl zu Vergrößern.<ref Name = "Vorlesungsunterlagen"></ref> | ||
| Zeile 27: | Zeile 38: | ||
:Durch die in die Gurtplatte ausgelagerte Bewehrung wird der Hebelarm der inneren Kräfte entsprechend umgelenkt und vergrößert sich somit. | :Durch die in die Gurtplatte ausgelagerte Bewehrung wird der Hebelarm der inneren Kräfte entsprechend umgelenkt und vergrößert sich somit. | ||
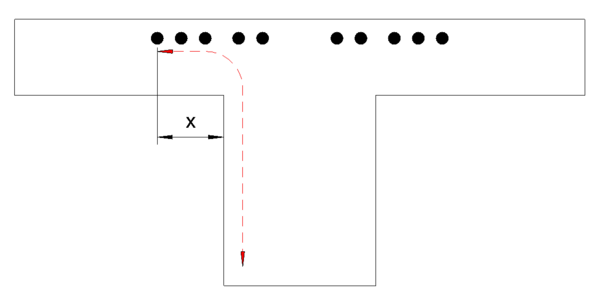
| − | [[Datei:Versatzmaß 1.png|mini|600px|none|Maß x]] | + | :[[Datei:Versatzmaß 1.png|mini|600px|none|Beispielhafte Darstellung für das Bestimmen vom Maß x]] |
| − | + | <br> | |
| − | |||
| + | :'''Verdeutlicht wird die Anwendung des Versatzmaßes am [[Zugkraftdeckung (Bsp.)|Berechnungsbeispiel]]. | ||
| + | ''' | ||
=Quellen= | =Quellen= | ||
Version vom 26. März 2024, 19:01 Uhr
Das Versatzmaß al ist eine Hilfsgröße, welche beim Verfahren der Zugkraftdeckung zur Berücksichtigung der Zuggurtkraftdifferenz in der Biegezugbewehrung benötigt wird. Der Betrag der Verschiebung al und damit der Betrag der Erhöhung der Zugkraft hängen direkt vom Fachwerkmodell der Querkraftbemessung ab.
Soll bei der Bemessung eines biegebeanspruchten Stahlbetonbauteils das Verfahren der Zugkraftdeckung auf grafische Weise angewendet werden, so wird hierfür das bestimmen des Versatzmaßes al erforderlich. Ebenfalls wird das Versatzmaß beim Ermitteln der Randzugkraft am Endauflager benötigt. Diese ist Grundlage für das Berechnen der Verankerungslänge.
Berechnung des Versatzmaßes
Allgemeine Formel für das Versatzmaß al:[1]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{l} = \cfrac{1}{2}\cdot(cot \theta-cot \alpha)\cdot z\ge 0}
cot θ... Druckstrebenneigungswinkel aus der Querkraftbemessung cot α... Neigungswinkel der Querkraftbewehrung z... Der Hebelarm der inneren Kräfte kann aus der Biegebemessung übernommen werden oder näherungsweise zu z=0,9·d angesetzt werden. Eventuell können durch erhebliche Normalkräfte (z.B. aus Vorspannung) auch kleinere Werte maßgebend werden.
Bei Bauteilen ohne Querkraftbewehrung gilt:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{l} = d}
d... statische Nutzhöhe
Bei Druckstrebenneigungswinkeln θ > 45° gilt:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{l} = \cfrac{z}{2}}
al ist gleichermaßen abhängig von α und θ
- für θ ↑ → al↓
- für α ↑ → al↑
- Besonderheit bei Plattenbalken:
- Wird bei Plattenbalken die Biegezugbewehrung aus dem Stegbereich ausgelagert (z.B. Stützbewehrung bei Zwischenauflagern), so ist das Versatzmaß al um den Abstand x des am weitesten vom Stegrand ausgelagerten Bewehrungsstahl zu Vergrößern.[1]
- Durch die in die Gurtplatte ausgelagerte Bewehrung wird der Hebelarm der inneren Kräfte entsprechend umgelenkt und vergrößert sich somit.
- Verdeutlicht wird die Anwendung des Versatzmaßes am Berechnungsbeispiel.