Versatzmaß: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | Das Versatzmaß a<sub>l</sub> ist eine Hilfsgröße, welche beim Verfahren der Zugkraftdeckung zur Berücksichtigung der Zuggurtkraftdifferenzkraft benötigt wird. Die Eingangsgrößen für die Bestimmungsgleichnung des Versatzmaßes ergeben sich aus dem Fachwerkmodell der Querkraftbemessung. | |
| − | Das Versatzmaß a<sub>l</sub> ist eine Hilfsgröße, welche beim Verfahren der | ||
| − | |||
| − | |||
=Berechnung des Versatzmaßes= | =Berechnung des Versatzmaßes= | ||
| + | [[Datei:Zuggurtkraftdifferenz 1.png|mini|400px|right|Fachwerkmodell nach EC2-1-1]<ref Name = "Vorlesungsunterlagen"></ref>]] | ||
Allgemeine Formel für das Versatzmaß a<sub>l</sub>:<ref Name = "Vorlesungsunterlagen">Bolle, G: Vorlesungsunterlagen Stahlbetonbau I, Hochschule Wismar, 2022</ref> | Allgemeine Formel für das Versatzmaß a<sub>l</sub>:<ref Name = "Vorlesungsunterlagen">Bolle, G: Vorlesungsunterlagen Stahlbetonbau I, Hochschule Wismar, 2022</ref> | ||
:<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(cot \theta-cot \alpha)\cdot z\ge 0</math> | :<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(cot \theta-cot \alpha)\cdot z\ge 0</math> | ||
| Zeile 12: | Zeile 10: | ||
| cot α... || Neigungswinkel der Querkraftbewehrung | | cot α... || Neigungswinkel der Querkraftbewehrung | ||
|- | |- | ||
| − | | z... || Hebelarm der inneren Kräfte kann aus der Biegebemessung übernommen werden oder näherungsweise zu z=0, | + | | z... || Der Hebelarm der inneren Kräfte kann aus der Biegebemessung übernommen werden oder näherungsweise zu z=0,9·d angesetzt werden. Eventuell können durch erhebliche Normalkräfte (z.B. aus Vorspannung) auch kleinere Werte maßgebend werden. |
| + | |} | ||
| + | |||
| + | Bei Bauteilen ohne Querkraftbewehrung gilt:<ref Name = "Springer">Bindseil, P.: Massivbau: Bemessung und Konstruktion im Stahlbetonbau mit Beispielen, 5. Auflage, Springer Vieweg Verlag, 2015</ref> | ||
| + | :<math>a_\mathrm{l} = d</math> | ||
| + | :::{| | ||
| + | | d... || statische Nutzhöhe | ||
|} | |} | ||
| − | |||
| − | a<sub>l</sub> ist gleichermaßen abhängig von α und θ | + | Bei Druckstrebenneigungswinkeln θ > 45° gilt:<ref Name = "Springer"></ref> |
| + | |||
| + | :<math>a_\mathrm{l} = \cfrac{z}{2}</math> | ||
| + | |||
| + | |||
| + | a<sub>l</sub> ist gleichermaßen abhängig von α und θ<ref Name = "Springer"></ref> | ||
:für θ ↑ → a<sub>l</sub>↓ | :für θ ↑ → a<sub>l</sub>↓ | ||
:für α ↑ → a<sub>l</sub>↑ | :für α ↑ → a<sub>l</sub>↑ | ||
| + | <br> | ||
| − | + | :'''Besonderheit bei Plattenbalken:''' | |
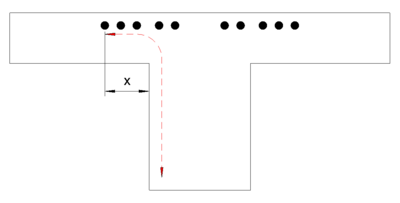
:Wird bei Plattenbalken die Biegezugbewehrung aus dem Stegbereich ausgelagert (z.B. Stützbewehrung bei Zwischenauflagern), so ist das Versatzmaß a<sub>l</sub> um den Abstand x des am weitesten vom Stegrand ausgelagerten Bewehrungsstahl zu Vergrößern.<ref Name = "Vorlesungsunterlagen"></ref> | :Wird bei Plattenbalken die Biegezugbewehrung aus dem Stegbereich ausgelagert (z.B. Stützbewehrung bei Zwischenauflagern), so ist das Versatzmaß a<sub>l</sub> um den Abstand x des am weitesten vom Stegrand ausgelagerten Bewehrungsstahl zu Vergrößern.<ref Name = "Vorlesungsunterlagen"></ref> | ||
| Zeile 27: | Zeile 36: | ||
:Durch die in die Gurtplatte ausgelagerte Bewehrung wird der Hebelarm der inneren Kräfte entsprechend umgelenkt und vergrößert sich somit. | :Durch die in die Gurtplatte ausgelagerte Bewehrung wird der Hebelarm der inneren Kräfte entsprechend umgelenkt und vergrößert sich somit. | ||
| − | [[Datei:Versatzmaß 1.png|mini| | + | :[[Datei:Versatzmaß 1.png|mini|400px|none|Beispielhafte Darstellung für das Bestimmen vom Maß x]] |
| + | <br> | ||
| + | |||
| + | :'''Verdeutlicht wird die Anwendung des Versatzmaßes am [[Zugkraftdeckung (Bsp.)|Berechnungsbeispiel]]. | ||
| + | ''' | ||
| + | =weitere Seiten zum Thema Versatzmaß= | ||
| + | |||
| + | [[Zugkraftdeckung]] | ||
| − | + | [[Zugkraftdeckung (Bsp.)]] | |
| + | |||
| + | [[Zuggurtkraftdifferenz]] | ||
=Quellen= | =Quellen= | ||
| Zeile 35: | Zeile 53: | ||
<references /> | <references /> | ||
| − | + | {{Seiteninfo | |
| + | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | ||
| + | |Status = Seite fertig, ungeprüft | ||
| + | }} | ||
[[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | ||
Aktuelle Version vom 1. April 2024, 18:33 Uhr
Das Versatzmaß al ist eine Hilfsgröße, welche beim Verfahren der Zugkraftdeckung zur Berücksichtigung der Zuggurtkraftdifferenzkraft benötigt wird. Die Eingangsgrößen für die Bestimmungsgleichnung des Versatzmaßes ergeben sich aus dem Fachwerkmodell der Querkraftbemessung.
Berechnung des Versatzmaßes

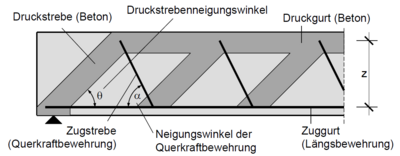
Fachwerkmodell nach EC2-1-1][1]
Allgemeine Formel für das Versatzmaß al:[1]
cot θ... Druckstrebenneigungswinkel aus der Querkraftbemessung cot α... Neigungswinkel der Querkraftbewehrung z... Der Hebelarm der inneren Kräfte kann aus der Biegebemessung übernommen werden oder näherungsweise zu z=0,9·d angesetzt werden. Eventuell können durch erhebliche Normalkräfte (z.B. aus Vorspannung) auch kleinere Werte maßgebend werden.
Bei Bauteilen ohne Querkraftbewehrung gilt:[2]
d... statische Nutzhöhe
Bei Druckstrebenneigungswinkeln θ > 45° gilt:[2]
al ist gleichermaßen abhängig von α und θ[2]
- für θ ↑ → al↓
- für α ↑ → al↑
- Besonderheit bei Plattenbalken:
- Wird bei Plattenbalken die Biegezugbewehrung aus dem Stegbereich ausgelagert (z.B. Stützbewehrung bei Zwischenauflagern), so ist das Versatzmaß al um den Abstand x des am weitesten vom Stegrand ausgelagerten Bewehrungsstahl zu Vergrößern.[1]
- Durch die in die Gurtplatte ausgelagerte Bewehrung wird der Hebelarm der inneren Kräfte entsprechend umgelenkt und vergrößert sich somit.
- Verdeutlicht wird die Anwendung des Versatzmaßes am Berechnungsbeispiel.
weitere Seiten zum Thema Versatzmaß
Quellen
Seiteninfo
|