Zugkraftdeckung (Bsp.): Unterschied zwischen den Versionen
| (25 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Folglich wird ein praxisnahes Berechnungsbeispiel zum Thema [[Zugkraftdeckung]] geführt. Dieses wird vergleichsweise händisch und mit zwei verschiedenen Bemessungssoftwares geführt. | Folglich wird ein praxisnahes Berechnungsbeispiel zum Thema [[Zugkraftdeckung]] geführt. Dieses wird vergleichsweise händisch und mit zwei verschiedenen Bemessungssoftwares geführt. | ||
| − | |||
| − | |||
=Statisches System und Belastung= | =Statisches System und Belastung= | ||
Betrachtet wird ein Durchlaufträger mit 2 Feldern unterschiedlicher Spannweite. Es handelt sich um einen Plattenbalkenquerschnitt, welcher frei drehbar gelagert ist. | Betrachtet wird ein Durchlaufträger mit 2 Feldern unterschiedlicher Spannweite. Es handelt sich um einen Plattenbalkenquerschnitt, welcher frei drehbar gelagert ist. | ||
| Zeile 9: | Zeile 7: | ||
Betonstabstahl: B500A | Betonstabstahl: B500A | ||
| + | <br> | ||
| − | [[Datei:System.png|mini| | + | [[Datei:System.png|mini|600px|none|System und Belastung]] |
=Berechnungsbeispiel - händisch= | =Berechnungsbeispiel - händisch= | ||
| − | Nachfolgend wird schrittweise die grafische händische Durchführung der Zugkraftdeckung an einem praxisnahen Berechnungsbeispiel erläutert. Hierbei werden auch die beiden Varianten hinsichtlich | + | Nachfolgend wird schrittweise die grafische händische Durchführung der Zugkraftdeckung an einem praxisnahen Berechnungsbeispiel erläutert. Hierbei werden auch die beiden Varianten hinsichtlich des Ansatzes der Tragfähigkeit der Bewehrung in der Verankerungslänge gegenübergestellt. |
==Grundlagen== | ==Grundlagen== | ||
*'''Momentengrenzlinie''' | *'''Momentengrenzlinie''' | ||
:Grundlage ist die Momentengrenzline (Bemessungswerte), welche aufgrund der verschiedenen Möglichkeiten der Laststellungen geeignet zu bestimmen ist (z.B. Schnittprinzip). | :Grundlage ist die Momentengrenzline (Bemessungswerte), welche aufgrund der verschiedenen Möglichkeiten der Laststellungen geeignet zu bestimmen ist (z.B. Schnittprinzip). | ||
| − | :[[Datei:Zugkraftdeckung (Bsp.) 2.png|mini| | + | :[[Datei:Zugkraftdeckung (Bsp.) 2.png|mini|600px|none|Vollständige Momentengrenzlinie in Diagrammform]] |
| + | <br> | ||
| − | :Um die Zugkraftdeckung zeichnerisch durchzuführen, sind schrittweise | + | :Um die Zugkraftdeckung zeichnerisch durchzuführen, sind schrittweise einzelne Werte des Verlaufes der Momentengrenzlinie zu bestimmen. Die Schrittweite ist so zu wählen, dass der Verlauf entsprechend „feinfühlig“ dargestellt wird. Im Falle des Beispiels führt ein Abstand von 0,5m zu einem zufriedenstellenden Ergebnis. Mit der Annahme der Anwendung des Schnittprinzips ist also alle 0,5m entlang der Systemlänge der Bemessungswert des Biegemomentes zu bestimmen. Aufgrund der Lagerungsbedingung am Zwischenauflager darf das Stützmoment abgemindert werden (Momentenausrundung). Dies ist ebenfalls zu berücksichtigen. |
| + | <br> | ||
*'''Ergebnisse aus der Biege- und Querkraftbemessung''' | *'''Ergebnisse aus der Biege- und Querkraftbemessung''' | ||
:Aus der Biegebemessung ist Anzahl, Durchmesser und Stahlgüte der Längsbewehrung bekannt. | :Aus der Biegebemessung ist Anzahl, Durchmesser und Stahlgüte der Längsbewehrung bekannt. | ||
| − | :Querschnitt des Plattenbalkens mit der gewählten Bewehrungsmenge und deren Anordnung am entsprechenden Betrachtungsschnitt (Querkraftbewehrung nicht dargestellt). Auch die statische Nutzhöhe d lässt sich aus der Grafik entnehmen. Aufgrund der einlagigen Anordnung ist diese im Beispiel stets 70 cm. | + | :Der Querschnitt des Plattenbalkens wird mit der gewählten Bewehrungsmenge und deren Anordnung am entsprechenden Betrachtungsschnitt (Querkraftbewehrung nicht dargestellt) in nachfolgender Grafik veranschaulicht. Auch die statische Nutzhöhe (d) lässt sich aus der Grafik entnehmen. Aufgrund der einlagigen Anordnung ist diese im Beispiel stets 70 cm. |
:[[Datei:Zugkraftdeckung (Bsp.) 3.png|mini|600px|none|Querschnitt mit Bewehrungsmengen]] | :[[Datei:Zugkraftdeckung (Bsp.) 3.png|mini|600px|none|Querschnitt mit Bewehrungsmengen]] | ||
| + | <br> | ||
| − | :Ebenfalls sind die Druckstrebenneigungswinkel aus der bereits vollzogenen Querkraftbemessung bekannt: | + | :Ebenfalls sind die '''Druckstrebenneigungswinkel''' aus der bereits vollzogenen Querkraftbemessung bekannt: |
::Am Auflager A und C ist θ = 18,4°→ cot θ = 3,00 | ::Am Auflager A und C ist θ = 18,4°→ cot θ = 3,00 | ||
| Zeile 38: | Zeile 40: | ||
:Der Neigungswinkel der Bügelbewehrung beträgt α = 90° →cot α = 0 | :Der Neigungswinkel der Bügelbewehrung beträgt α = 90° →cot α = 0 | ||
| − | :Die Bemessungswerte der Querkräfte an den Endauflagern betragen bei Auflager A = 290, | + | :Die Bemessungswerte der Querkräfte an den Endauflagern betragen bei Auflager A = 290,99 kN und bei B = 236,05 kN. |
==Bestimmen der M/z - Linie (Zugkraft aufgrund von Biegemomenten)== | ==Bestimmen der M/z - Linie (Zugkraft aufgrund von Biegemomenten)== | ||
Die M/z Linie lässt sich aus der Momentengrenzline bestimmen. Ziel ist es, den Verlauf der Stahlzugkraft F<sub>sd</sub> aufgrund von Biegemomenten in Diagrammform darzustellen. Um die entsprechenden Werte für das Zugkraftdiagramm zu erhalten, ist jeder einzelne Bemessungswert aus der Momentengrenzlinie durch den Hebelarm der inneren Kräfte (z) zu dividieren. Man erhält somit aus dem Moment M<sub>Ed</sub> [kNm] die Stahlzugkraft F<sub>sd</sub> [kN]. | Die M/z Linie lässt sich aus der Momentengrenzline bestimmen. Ziel ist es, den Verlauf der Stahlzugkraft F<sub>sd</sub> aufgrund von Biegemomenten in Diagrammform darzustellen. Um die entsprechenden Werte für das Zugkraftdiagramm zu erhalten, ist jeder einzelne Bemessungswert aus der Momentengrenzlinie durch den Hebelarm der inneren Kräfte (z) zu dividieren. Man erhält somit aus dem Moment M<sub>Ed</sub> [kNm] die Stahlzugkraft F<sub>sd</sub> [kN]. | ||
| − | Die Stahlzugkraft F<sub>sd</sub> errechnet sich somit zu: | + | Die Stahlzugkraft F<sub>sd</sub> errechnet sich somit zu:<ref Name = "Vorlesungsunterlagen">Bolle, G: Vorlesungsunterlagen Stahlbetonbau I, Hochschule Wismar, 2022</ref> |
:<math>F_\mathrm{sd}=\cfrac{M_\mathrm{Ed}}{z}+N_\mathrm{Ed}</math> | :<math>F_\mathrm{sd}=\cfrac{M_\mathrm{Ed}}{z}+N_\mathrm{Ed}</math> | ||
:::{| | :::{| | ||
| Zeile 51: | Zeile 53: | ||
| N<sub>Ed</sub>... || Bemessungswert des einwirkenden Normalkraft (keine einwirkende Normalkraft vorhanden→ entfällt somit) | | N<sub>Ed</sub>... || Bemessungswert des einwirkenden Normalkraft (keine einwirkende Normalkraft vorhanden→ entfällt somit) | ||
|} | |} | ||
| + | <br> | ||
| + | |||
Aufgrund des sich immer wiederholenden Berechnungsschrittes wird dieser folglich nur einmal exemplarisch am maximalen Biegemoment in Feld 1 veranschaulicht: | Aufgrund des sich immer wiederholenden Berechnungsschrittes wird dieser folglich nur einmal exemplarisch am maximalen Biegemoment in Feld 1 veranschaulicht: | ||
:<math>M_\mathrm{Ed}=413,2 kNm </math> | :<math>M_\mathrm{Ed}=413,2 kNm </math> | ||
| Zeile 59: | Zeile 63: | ||
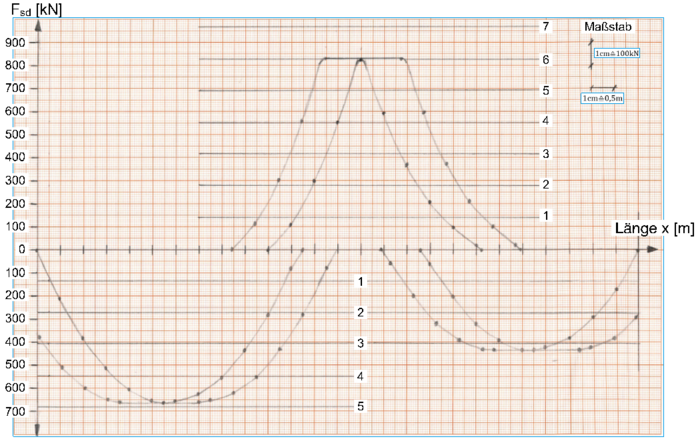
Nach dieser Vorgehensweise sind alle Werte aus der Momentengrenzlinie in die entsprechende Stahlzugkraft umzurechnen. Eine Tabelle kann hierfür sehr sinnvoll sein: | Nach dieser Vorgehensweise sind alle Werte aus der Momentengrenzlinie in die entsprechende Stahlzugkraft umzurechnen. Eine Tabelle kann hierfür sehr sinnvoll sein: | ||
| − | + | [[Datei:Zugkraftdeckung (Bsp.) 4.png|mini|600px|none|Tabelle]] | |
| + | <br> | ||
| − | Sind alle Werte bestimmt, lassen sich diese anhand ihrer Koordinaten im Zugkraftdiagramm eintragen. Bei der händischen Durchführung eignet sich hierfür Millimeterpapier. Die Maßstäbe können hierbei | + | Sind alle Werte bestimmt, lassen sich diese anhand ihrer Koordinaten im Zugkraftdiagramm eintragen. Bei der händischen Durchführung eignet sich hierfür Millimeterpapier. Die Maßstäbe können hierbei frei gewählt werden. |
| − | [[Datei:Zugkraftdeckung (Bsp.) 5.png|mini| | + | [[Datei:Zugkraftdeckung (Bsp.) 5.png|mini|700px|none|Im Diagramm eingetragene Punkte]] |
Sind alle Punkte im Diagramm eingetragen, lassen sich diese entsprechend verbinden, um den Zugkraftverlauf zu erhalten. | Sind alle Punkte im Diagramm eingetragen, lassen sich diese entsprechend verbinden, um den Zugkraftverlauf zu erhalten. | ||
| − | [[Datei:Zugkraftdeckung (Bsp.) 6.png|mini| | + | [[Datei:Zugkraftdeckung (Bsp.) 6.png|mini|700px|none|M/z - Linie (Zugkraft aufgrund von Biegemomenten)]] |
==F<sub>sd</sub> – Linie (Zugkraft aufgrund von Biegemomenten und Querkraft)== | ==F<sub>sd</sub> – Linie (Zugkraft aufgrund von Biegemomenten und Querkraft)== | ||
Um den tatsächlichen Verlauf der Stahlzugkraft aufgrund von Biegemoment und Querkraft im Zugkraftdiagramm darzustellen, ist die [[Zuggurtkraftdifferenz]] zu berücksichtigen. Bei der zeichnerischen Durchführung erfolgt dies durch horizontales Versetzen der M/z – Linie um das [[Versatzmaß]] a<sub>l</sub>. | Um den tatsächlichen Verlauf der Stahlzugkraft aufgrund von Biegemoment und Querkraft im Zugkraftdiagramm darzustellen, ist die [[Zuggurtkraftdifferenz]] zu berücksichtigen. Bei der zeichnerischen Durchführung erfolgt dies durch horizontales Versetzen der M/z – Linie um das [[Versatzmaß]] a<sub>l</sub>. | ||
| + | <br> | ||
| − | Das [[Versatzmaß]] a<sub>l</sub> ergibt sich zu: | + | Das [[Versatzmaß]] a<sub>l</sub> ergibt sich zu:<ref Name = "Vorlesungsunterlagen"></ref> |
:<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(cot \theta-cot \alpha)\cdot z\ge 0</math> | :<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(cot \theta-cot \alpha)\cdot z\ge 0</math> | ||
:::{| | :::{| | ||
| Zeile 81: | Zeile 87: | ||
| z... || Der Hebelarm der inneren Kräfte errechnet sich im Falle des Beispiels aus der statischen Nutzhöhe zu 0,9 · d. | | z... || Der Hebelarm der inneren Kräfte errechnet sich im Falle des Beispiels aus der statischen Nutzhöhe zu 0,9 · d. | ||
|} | |} | ||
| − | Aufgrund der unterschiedlichen Druckstrebenneigungswinkel | + | <br> |
| + | |||
| + | Aufgrund der unterschiedlichen Druckstrebenneigungswinkel pro Bemessungsabschnitt, ist das Versatzmaß für das betrachtete Beispiel mehrfach zu bestimmen. | ||
| + | |||
| + | Der Hebelarm der inneren Kräfte bleibt auf gesamter Bauteillänge konstant und ergibt sich zu: | ||
| + | |||
:<math>z=0,9\cdot d = 0,9 \cdot 0,7m = 0,63m</math> | :<math>z=0,9\cdot d = 0,9 \cdot 0,7m = 0,63m</math> | ||
| + | |||
Der Neigungswinkel der Bügelbewehrung beträgt α = 90° →cot α = 0 | Der Neigungswinkel der Bügelbewehrung beträgt α = 90° →cot α = 0 | ||
| Zeile 93: | Zeile 105: | ||
Zu beachten: | Zu beachten: | ||
| − | Am Zwischenauflager (Auflager B) ist die Biegezugbewehrung teilweise aus dem Stegbereich in die Gurtplatte ausgelagert. Hier ist das Versatzmaß um den Abstand der vom Stegrand am weitesten ausgelagerten Bewehrung zu vergrößern (Maß x). | + | Am Zwischenauflager (Auflager B) ist die '''obere''' Biegezugbewehrung teilweise aus dem Stegbereich in die Gurtplatte ausgelagert. Hier ist das [[Versatzmaß]] um den Abstand der vom Stegrand am weitesten ausgelagerten Bewehrung zu vergrößern (Maß x). |
[[Datei:Zugkraftdeckung (Bsp.) 7.png|mini|200px|none|Maß x (Auslagerung)]] | [[Datei:Zugkraftdeckung (Bsp.) 7.png|mini|200px|none|Maß x (Auslagerung)]] | ||
| Zeile 99: | Zeile 111: | ||
Am Auflager B links ist cot θ = 2,14 | Am Auflager B links ist cot θ = 2,14 | ||
| − | Somit ergibt sich das Versatzmaß zu: | + | Somit ergibt sich das Versatzmaß entsprechend der Lage der Bewehrung zu: |
| + | |||
| + | :obere Bewehrung: | ||
:<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(2,14-0)\cdot 0,63+0,1=0,77m\ge 0</math> | :<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(2,14-0)\cdot 0,63+0,1=0,77m\ge 0</math> | ||
| + | |||
| + | :untere Bewehrung: | ||
| + | |||
| + | :<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(2,14-0)\cdot 0,63=0,67m\ge 0</math> | ||
Am Auflager B rechts ist cot θ = 2,37 | Am Auflager B rechts ist cot θ = 2,37 | ||
| − | Somit ergibt sich das Versatzmaß zu: | + | Somit ergibt sich das Versatzmaß entsprechend der Lage der Bewehrung zu: |
| + | |||
| + | :obere Bewehrung: | ||
:<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(2,37-0)\cdot 0,63+0,1=0,85m\ge 0</math> | :<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(2,37-0)\cdot 0,63+0,1=0,85m\ge 0</math> | ||
| − | + | :untere Bewehrung: | |
| − | + | ||
| + | :<math>a_\mathrm{l} = \cfrac{1}{2}\cdot(2,37-0)\cdot 0,63=0,75m\ge 0</math> | ||
| + | <br> | ||
| − | + | Mit den ermittelten Versatzmaßen lassen sich die zuvor im Zugkraftdiagramm ermittelten Punkte horizontal verschieben. Zu beachten ist, dass das jeweils korrekte Versatzmaß an entsprechender Stelle verwendet wird. Hierbei sind die Auflagerlinien und die Extremstellen im Diagramm als Orientierungspunkte für die Anwendung des entsprechenden Versatzmaßes anzusehen. Versetzt wird jeweils immer nach „außen“. | |
| + | [[Datei:Zugkraftdeckung (Bsp.) 8.png|mini|700px|none|Versetzte Punkte]] | ||
| + | <br> | ||
| − | [[Datei:Zugkraftdeckung (Bsp.) 9.png|mini| | + | Sind alle versetzten Punkte im Diagramm eingetragen, lassen sich diese entsprechend verbinden, um den endgültigen Zugkraftverlauf zu erhalten. Optisch deutlich erkennbar ist nun, dass die Zugkraftlinien horizontal um das Versatzmaß parallelverschoben sind. |
| + | |||
| + | [[Datei:Zugkraftdeckung (Bsp.) 9.png|mini|700px|none|Versetzte Linie]] | ||
==Eintragen der Bewehrungshorizonte== | ==Eintragen der Bewehrungshorizonte== | ||
Aus der bereits vollzogenen Biegebemessung sind Durchmesser und Anzahl der Bewehrungsstäbe als Biegezugbewehrung bekannt. Jeder einzelne Stab kann aufgrund seiner Querschnittsfläche und der Stahlfestigkeit eine entsprechende Zugkraft F<sub>⌀</sub> aufnehmen. | Aus der bereits vollzogenen Biegebemessung sind Durchmesser und Anzahl der Bewehrungsstäbe als Biegezugbewehrung bekannt. Jeder einzelne Stab kann aufgrund seiner Querschnittsfläche und der Stahlfestigkeit eine entsprechende Zugkraft F<sub>⌀</sub> aufnehmen. | ||
| − | Die pro Bewehrungsstahl aufnehmbare Zugkraft F<sub>⌀</sub> errechnet sich zu: | + | Die pro Bewehrungsstahl aufnehmbare Zugkraft F<sub>⌀</sub> errechnet sich zu:<ref Name = "Vorlesungsunterlagen"></ref> |
:<math>F_\mathrm{\varnothing_{}} = A_\mathrm{s\varnothing_{}}\cdot f_\mathrm{yd}</math> | :<math>F_\mathrm{\varnothing_{}} = A_\mathrm{s\varnothing_{}}\cdot f_\mathrm{yd}</math> | ||
| Zeile 127: | Zeile 153: | ||
| f<sub>yd</sub>... || Bemessungswert der Stahlstreckgrenze | | f<sub>yd</sub>... || Bemessungswert der Stahlstreckgrenze | ||
|} | |} | ||
| + | <br> | ||
Verbaut werden Bewehrungsstähle B500A mit einem Durchmesser von 20 mm. | Verbaut werden Bewehrungsstähle B500A mit einem Durchmesser von 20 mm. | ||
| Zeile 135: | Zeile 162: | ||
:<math>F_\mathrm{\varnothing_{}} = 3,14\cdot 43,5=136,6kN</math> | :<math>F_\mathrm{\varnothing_{}} = 3,14\cdot 43,5=136,6kN</math> | ||
| + | <br> | ||
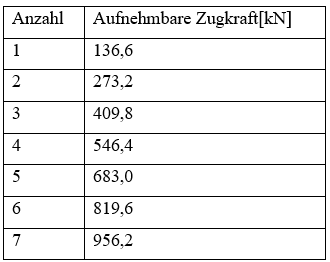
Mit zunehmender Anzahl der Bewehrungsstähle kann kontinuierlich mehr Zugkraft aufgenommen werden. In nachfolgender Tabelle wurde die Zugkraft entsprechend der Stabanzahl aufsummiert. | Mit zunehmender Anzahl der Bewehrungsstähle kann kontinuierlich mehr Zugkraft aufgenommen werden. In nachfolgender Tabelle wurde die Zugkraft entsprechend der Stabanzahl aufsummiert. | ||
[[Datei:Zugkraftdeckung (Bsp.) 10.png|mini|400px|none|Tabelle - aufnehmbare Zugkräfte]] | [[Datei:Zugkraftdeckung (Bsp.) 10.png|mini|400px|none|Tabelle - aufnehmbare Zugkräfte]] | ||
| + | <br> | ||
Im Zugkraftdiagramm sind entsprechend der aufnehmbaren Zugkraft die einzelnen Bewehrungsstähle als sogenannte „Bewehrungshorizonte“ als feine Orientierungslinien einzutragen. | Im Zugkraftdiagramm sind entsprechend der aufnehmbaren Zugkraft die einzelnen Bewehrungsstähle als sogenannte „Bewehrungshorizonte“ als feine Orientierungslinien einzutragen. | ||
| − | [[Datei:Zugkraftdeckung (Bsp.) 11.png|mini| | + | [[Datei:Zugkraftdeckung (Bsp.) 11.png|mini|700px|none|Eingetragene Bewehrungshorizonte]] |
| + | <br> | ||
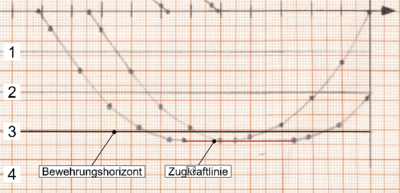
| − | Auszug aus Feld 2: Die durch 3 Bewehrungsstähle aufnehmbare Zugkraft unterschreitet offensichtlich geringfügig die mit der Zugkraftlinie dargestellte einwirkende Zugkraft. Diese geringe Abweichung ist jedoch akzeptabel. Zurückzuführen ist dies auf den Hebelarm der inneren Kräfte z. Die Biegebemessung und damit die Bewehrungswahl erfolgt mit dem exakten Wert für z. Die Zugkraftlinie hingegen wird auf der sicheren Seite liegend vereinfacht mit z = 0,9 · d bestimmt. Hierdurch wird im Zugkraftdiagramm eine teilweise etwas höhere Stahlzugkraft dargestellt | + | Auszug aus Feld 2: Die durch 3 Bewehrungsstähle aufnehmbare Zugkraft unterschreitet offensichtlich geringfügig die mit der Zugkraftlinie dargestellte einwirkende Zugkraft. Diese geringe Abweichung ist jedoch akzeptabel. Zurückzuführen ist dies auf den Hebelarm der inneren Kräfte (z). Die Biegebemessung und damit die Bewehrungswahl erfolgt mit dem exakten Wert für z. Die Zugkraftlinie hingegen wird auf der sicheren Seite liegend vereinfacht mit z = 0,9 · d bestimmt. Hierdurch wird im Zugkraftdiagramm eine teilweise etwas höhere Stahlzugkraft dargestellt als tatsächlich auftreten wird. |
[[Datei:Zugkraftdeckung (Bsp.) 12.png|mini|400px|none|geringe Unterschreitung der Zugkraftlinie]] | [[Datei:Zugkraftdeckung (Bsp.) 12.png|mini|400px|none|geringe Unterschreitung der Zugkraftlinie]] | ||
| Zeile 162: | Zeile 192: | ||
===Variante a - Zugkraftdeckungslinie „Stufenfunktion“ (nach DIN 1045-1)=== | ===Variante a - Zugkraftdeckungslinie „Stufenfunktion“ (nach DIN 1045-1)=== | ||
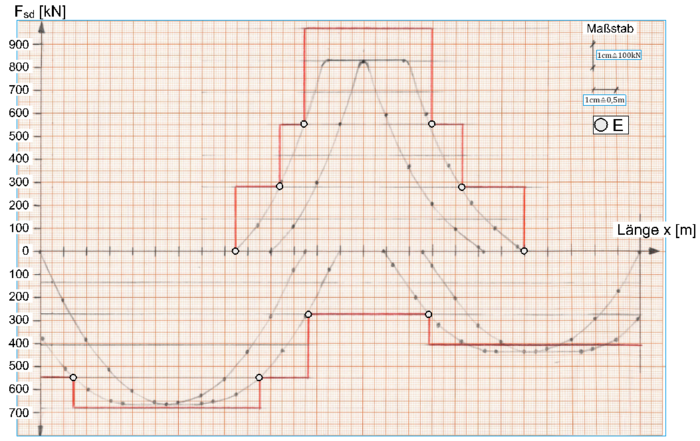
| − | Vollständige Zugkraftdeckungslinie „Stufenfunktion“ (rote Linie) | + | Vollständige Zugkraftdeckungslinie „Stufenfunktion“ (rote Linie): |
| + | |||
| + | Orientierungspunkte beim Zeichnen sind die Bewehrungshorizonte und die rechnerischen Endpunkten E der Bewehrung. Abstufungsschritte wie vorab beschrieben. | ||
| − | [[Datei:Zugkraftdeckung (Bsp.) 13.png|mini| | + | [[Datei:Zugkraftdeckung (Bsp.) 13.png|mini|700px|none|Zugkraftdeckungslinie „Stufenfunktion“]] |
| + | <br> | ||
===Bestimmen der Verankerungslängen (Zwischenschritt)=== | ===Bestimmen der Verankerungslängen (Zwischenschritt)=== | ||
| − | Für beide Varianten der | + | Für beide Varianten der Zugkraftdeckung sind die Maße der Verankerungslängen erforderlich. Bei Variante b) werden die Verankerungslängen bereits beim Zeichnen der Zugkraftdeckungslinie benötigt. |
Exemplarisch wird das Errechnen der erforderlichen Verankerungslänge an 2 verschiedenen Positionen veranschaulicht. Am Zwischenauflager läuft die nicht abgestufte untere Bewehrung durch. Der Nachweis der Verankerungslänge entfällt hier somit. | Exemplarisch wird das Errechnen der erforderlichen Verankerungslänge an 2 verschiedenen Positionen veranschaulicht. Am Zwischenauflager läuft die nicht abgestufte untere Bewehrung durch. Der Nachweis der Verankerungslänge entfällt hier somit. | ||
| − | ====Verankerung am Endauflager==== | + | ====Verankerung am Endauflager<ref Name = "Vorlesungsunterlagen"></ref>==== |
:*'''Ermitteln der Randzugkraft F<sub>Ed</sub> (Zugkraft am Endauflager):''' | :*'''Ermitteln der Randzugkraft F<sub>Ed</sub> (Zugkraft am Endauflager):''' | ||
| Zeile 184: | Zeile 217: | ||
::<math>F_\mathrm{Ed} =290,99\cdot\cfrac{94,5}{63,0}=436,5 kN</math> | ::<math>F_\mathrm{Ed} =290,99\cdot\cfrac{94,5}{63,0}=436,5 kN</math> | ||
::<math>F_\mathrm{Ed} =\cfrac{290,99}{2}=145,5 kN</math> | ::<math>F_\mathrm{Ed} =\cfrac{290,99}{2}=145,5 kN</math> | ||
| − | ::'''Maßgebend: 436,50 kN''' | + | :::'''Maßgebend: 436,50 kN''' |
:*'''Ermitteln, des zur Aufnahme der Randzugkraft erforderlichen Bewehrungsquerschnitt''' | :*'''Ermitteln, des zur Aufnahme der Randzugkraft erforderlichen Bewehrungsquerschnitt''' | ||
| Zeile 199: | Zeile 232: | ||
| A<sub>s,vorh</sub>... || Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe | | A<sub>s,vorh</sub>... || Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe | ||
|} | |} | ||
| + | <br> | ||
| + | |||
::4⌀20 werden bis ins Auflager geführt | ::4⌀20 werden bis ins Auflager geführt | ||
::Hieraus errechnet sich die vorhandene Querschnittsfläche: | ::Hieraus errechnet sich die vorhandene Querschnittsfläche: | ||
::<math>A_\mathrm{s,vorh} = 4\cdot 3,14=12,56 cm^2</math> | ::<math>A_\mathrm{s,vorh} = 4\cdot 3,14=12,56 cm^2</math> | ||
| + | <br> | ||
::Somit errechnet sich die Stahlspannung zu: | ::Somit errechnet sich die Stahlspannung zu: | ||
| Zeile 207: | Zeile 243: | ||
:*'''Grundwert der Verankerungslänge''' | :*'''Grundwert der Verankerungslänge''' | ||
| − | :Guter Verbund (Bewehrung liegt unten), für Beton C25/30 ist somit f<sub>bd</sub> = 2,69 N/mm<sup>2</sup> | + | ::Guter Verbund (Bewehrung liegt unten), für Beton C25/30 ist somit f<sub>bd</sub> = 2,69 N/mm<sup>2</sup> |
| − | :<math>l_{b,rqd} = \frac{\varnothing_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}}</math> | + | ::<math>l_{b,rqd} = \frac{\varnothing_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}}</math> |
:::{| | :::{| | ||
| f<sub>bd</sub>... || Verbundfestigkeit | | f<sub>bd</sub>... || Verbundfestigkeit | ||
| Zeile 214: | Zeile 250: | ||
| ⌀<sub>s</sub>... || Stabdurchmesser | | ⌀<sub>s</sub>... || Stabdurchmesser | ||
|} | |} | ||
| − | :<math>l_{b,rqd} = \frac{2}{4} \cdot \frac{34,74}{0,269}=64,57 cm</math> | + | ::<math>l_{b,rqd} = \frac{2}{4} \cdot \frac{34,74}{0,269}=64,57 cm</math> |
:*'''Bemessungswert der Verankerungslänge''' | :*'''Bemessungswert der Verankerungslänge''' | ||
| − | :::Beiwerte: | + | :::*Beiwerte: |
:::-Verankerung mit Winkelhaken → α<sub>1</sub>=0,7 | :::-Verankerung mit Winkelhaken → α<sub>1</sub>=0,7 | ||
| − | ::: | + | :::(Aufgrund der begrenzten Platzverhältnisse zur Verankerung am Endauflager musste die Verankerungsform Winkelhaken gewählt werden) |
:::-Keine angeschweißten Querstäbe → α<sub>4</sub>=1,0 | :::-Keine angeschweißten Querstäbe → α<sub>4</sub>=1,0 | ||
:::-direkte Lagerung → α<sub>5</sub>=2/3 | :::-direkte Lagerung → α<sub>5</sub>=2/3 | ||
| − | :<math>l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}</math> | + | ::<math>l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}</math> |
| − | :<math>l_{b,eq} = 0,7\cdot 1\cdot\frac{2}{3}\cdot 28,61 = 20,10cm</math> | + | ::<math>l_{b,eq} = 0,7\cdot 1\cdot\frac{2}{3}\cdot 28,61 = 20,10cm</math> |
:*'''Mindestwert der Verankerungslänge''' | :*'''Mindestwert der Verankerungslänge''' | ||
| − | :<math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> | + | ::<math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> |
| − | :<math>l_{b,min} = 0,3\cdot 1\cdot\frac{2}{3}\cdot 1 \cdot \frac{2}{4} \cdot \frac{43,5}{0,269}=16,2 cm</math> | + | ::<math>l_{b,min} = 0,3\cdot 1\cdot\frac{2}{3}\cdot 1 \cdot \frac{2}{4} \cdot \frac{43,5}{0,269}=16,2 cm</math> |
| − | :<math>l_{b,min} =10\cdot \frac{2}{3}\cdot 2 = 13,3 cm </math> | + | ::<math>l_{b,min} =10\cdot \frac{2}{3}\cdot 2 = 13,3 cm </math> |
| − | :→ Mindestverankerungslänge wird nicht | + | ::→ Mindestverankerungslänge wird nicht maßgebend |
| + | <br> | ||
:'''Nachweis:''' | :'''Nachweis:''' | ||
| Zeile 237: | Zeile 274: | ||
:Unter der Annahme einer Betondeckung von c<sub>nom</sub> = 5 cm werden die Bewehrungsstähle auf gesamter Auflagerbreite mit Winkelhaken verankert. | :Unter der Annahme einer Betondeckung von c<sub>nom</sub> = 5 cm werden die Bewehrungsstähle auf gesamter Auflagerbreite mit Winkelhaken verankert. | ||
:<math>l_{b,vorh} = t-c_{nom}=35-5 =30 cm\ge l_{b,eq} = 20,10 cm</math> '''→ Nachweis erfüllt''' | :<math>l_{b,vorh} = t-c_{nom}=35-5 =30 cm\ge l_{b,eq} = 20,10 cm</math> '''→ Nachweis erfüllt''' | ||
| + | <br> | ||
| − | ====Verankerung außerhalb von Auflagern==== | + | ====Verankerung außerhalb von Auflagern<ref Name = "Vorlesungsunterlagen"></ref>==== |
| − | Verankerung der unteren Bewehrung in Feld 1 | + | Verankerung der unteren Bewehrung in Feld 1: |
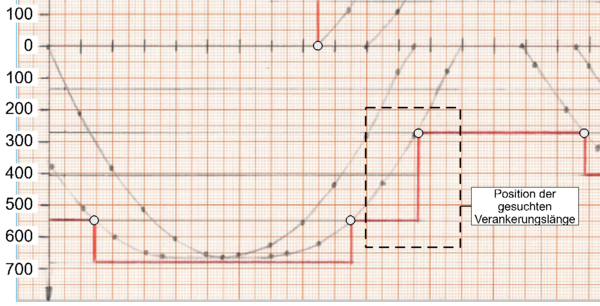
| − | [[Datei:Zugkraftdeckung (Bsp.) 14.png|mini| | + | [[Datei:Zugkraftdeckung (Bsp.) 14.png|mini|600px|none|Position der gesuchten Verankerungslänge]] |
| + | <br> | ||
:*'''Ermittlung der Stahlspannung am rechnerischen Endpunkt E''' | :*'''Ermittlung der Stahlspannung am rechnerischen Endpunkt E''' | ||
| − | :Hierbei ist das Verhältnis aus erforderlicher und vorhandener Bewehrung zu bilden. | + | ::Hierbei ist das Verhältnis aus erforderlicher und vorhandener Bewehrung zu bilden. |
| − | :2 Stäbe werden noch gebraucht | + | ::*2 Stäbe werden noch gebraucht |
| + | |||
| + | ::*4 Stäbe sind vorhanden | ||
| − | :Somit ist: | + | ::Somit ist: |
| − | :A<sub>s,erf</sub>=6,28cm<sup>2</sup> (2⌀20) | + | ::A<sub>s,erf</sub>=6,28cm<sup>2</sup> (2⌀20) |
| − | :A<sub>s,vorh</sub>= | + | ::A<sub>s,vorh</sub>=12,56cm<sup>2</sup> (5⌀20) |
::<math>\sigma_\mathrm{sd} =\cfrac{A_\mathrm{s,erf}}{A_\mathrm{s,vorh}}\cdot f_\mathrm{yd}</math> | ::<math>\sigma_\mathrm{sd} =\cfrac{A_\mathrm{s,erf}}{A_\mathrm{s,vorh}}\cdot f_\mathrm{yd}</math> | ||
| Zeile 254: | Zeile 295: | ||
| A<sub>s,vorh</sub>... || Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe | | A<sub>s,vorh</sub>... || Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe | ||
|} | |} | ||
| − | :Die Stahlspannung errechnet sich zu: | + | <br> |
| − | ::<math>\sigma_\mathrm{sd} =\cfrac{6,28}{ | + | |
| + | ::Die Stahlspannung errechnet sich zu: | ||
| + | ::<math>\sigma_\mathrm{sd} =\cfrac{6,28}{12,56}\cdot 43,5=21,75 kN/cm^2</math> | ||
:*'''Grundwert der Verankerungslänge''' | :*'''Grundwert der Verankerungslänge''' | ||
| − | :Guter Verbund (Bewehrung liegt unten), für Beton C25/30 ist somit f<sub>bd</sub> = 2,69 N/mm<sup>2</sup> | + | ::Guter Verbund (Bewehrung liegt unten), für Beton C25/30 ist somit f<sub>bd</sub> = 2,69 N/mm<sup>2</sup> |
| − | :<math>l_{b,rqd} = \frac{\varnothing_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}}</math> | + | ::<math>l_{b,rqd} = \frac{\varnothing_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}}</math> |
:::{| | :::{| | ||
| f<sub>bd</sub>... || Verbundfestigkeit | | f<sub>bd</sub>... || Verbundfestigkeit | ||
| Zeile 265: | Zeile 308: | ||
| ⌀<sub>s</sub>... || Stabdurchmesser | | ⌀<sub>s</sub>... || Stabdurchmesser | ||
|} | |} | ||
| − | :<math>l_{b,rqd} = \frac{2}{4} \cdot \frac{ | + | <br> |
| + | |||
| + | :<math>l_{b,rqd} = \frac{2}{4} \cdot \frac{21,75}{0,269}=40,43 cm</math> | ||
:*'''Bemessungswert der Verankerungslänge''' | :*'''Bemessungswert der Verankerungslänge''' | ||
| Zeile 272: | Zeile 317: | ||
:::-Keine angeschweißten Querstäbe → α<sub>4</sub>=1,0 | :::-Keine angeschweißten Querstäbe → α<sub>4</sub>=1,0 | ||
:::-keine Querdruck- oder Querzugspannungen → α<sub>5</sub>=1,0 | :::-keine Querdruck- oder Querzugspannungen → α<sub>5</sub>=1,0 | ||
| − | :<math>l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}</math> | + | ::<math>l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}</math> |
| − | :<math>l_{b,eq} = 1,0\cdot 1,0\cdot 1,0\cdot | + | ::<math>l_{b,eq} = 1,0\cdot 1,0\cdot 1,0\cdot 40,43 = 40,43 cm</math> |
:*'''Mindestwert der Verankerungslänge''' | :*'''Mindestwert der Verankerungslänge''' | ||
| − | :<math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> | + | ::<math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} </math> |
| − | :<math>l_{b,min} = 0,3\cdot 1,0\cdot1,0\cdot 1,0 \cdot \frac{2}{4} \cdot \frac{43,5}{0,269}=24,26 cm</math> | + | ::<math>l_{b,min} = 0,3\cdot 1,0\cdot1,0\cdot 1,0 \cdot \frac{2}{4} \cdot \frac{43,5}{0,269}=24,26 cm</math> |
| − | :<math>l_{b,min} =10\cdot 1\cdot 2 = 20 cm </math> | + | ::<math>l_{b,min} =10\cdot 1\cdot 2 = 20 cm </math> |
| − | :→ Mindestverankerungslänge wird nicht Maßgebend | + | ::→ Mindestverankerungslänge wird nicht Maßgebend |
| + | <br> | ||
:'''Nachweis:''' | :'''Nachweis:''' | ||
| − | :gewählte Verankerungslänge → | + | :gewählte Verankerungslänge → 45 cm |
| − | :<math>l_{b,vorh} = | + | :<math>l_{b,vorh} =45 cm\ge l_{b,eq} = 40,43 cm</math> '''→ Nachweis erfüllt''' |
| + | <br> | ||
'''Nach dieser Vorgehensweise sind die Verankerungen aller Stabenden nachzuweisen.''' | '''Nach dieser Vorgehensweise sind die Verankerungen aller Stabenden nachzuweisen.''' | ||
| − | + | <br> | |
| − | Mit den errechneten Verankerungslängen lässt sich folglich nun auch die Zugkraftdeckungslinie für Variante b erstellen | + | |
| + | → Mit den errechneten Verankerungslängen lässt sich folglich nun auch die Zugkraftdeckungslinie für Variante b erstellen | ||
===Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“=== | ===Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“=== | ||
Für diese Variante sind die Verankerungslängen bereits vor dem Zeichnen der Zugkraftdeckungslinie anhand der Abstufungsschritte zu ermitteln. | Für diese Variante sind die Verankerungslängen bereits vor dem Zeichnen der Zugkraftdeckungslinie anhand der Abstufungsschritte zu ermitteln. | ||
| − | Vollständige Zugkraftdeckungslinie „anschmiegende Funktion“ (rote Linie) | + | Vollständige Zugkraftdeckungslinie „anschmiegende Funktion“ (rote Linie): |
| + | |||
| + | Orientierungspunkte beim Zeichnen sind die Bewehrungshorizonte und die rechnerischen Endpunkten E der Bewehrung. Die Bereiche mit linearen Verlauf lassen sich über die entsprechende Verankerungslänge konstruieren. Abstufungsschritte wie eingangs beschrieben. | ||
| − | [[Datei:Zugkraftdeckung (Bsp.) 15.png|mini| | + | [[Datei:Zugkraftdeckung (Bsp.) 15.png|mini|700px|none|Zugkraftdeckungslinie „anschmiegende Funktion“]] |
| + | <br> | ||
==Bewehrungslängen ermitteln== | ==Bewehrungslängen ermitteln== | ||
| − | Über den gewählten Maßstab lassen sich anhand der Zugkraftdeckungslinie die tatsächlichen Stablängen ermitteln. Die Verankerungslängen sind hierbei stets zu berücksichtigen | + | Über den gewählten Maßstab lassen sich anhand der Zugkraftdeckungslinie die tatsächlichen Stablängen und deren Position im Bauteil ermitteln. Die Verankerungslängen sind hierbei stets zu berücksichtigen. Zu beachten ist bei der Längenermittlung ebenfalls die Auflagerbreite der Endauflager. Denn das Zugkraftdiagramm bezieht sich nur auf die Abstände der rechnerischen Auflagerlinien. |
| + | <br> | ||
| + | |||
:*'''Variante a - Zugkraftdeckungslinie „Stufenfunktion“''' | :*'''Variante a - Zugkraftdeckungslinie „Stufenfunktion“''' | ||
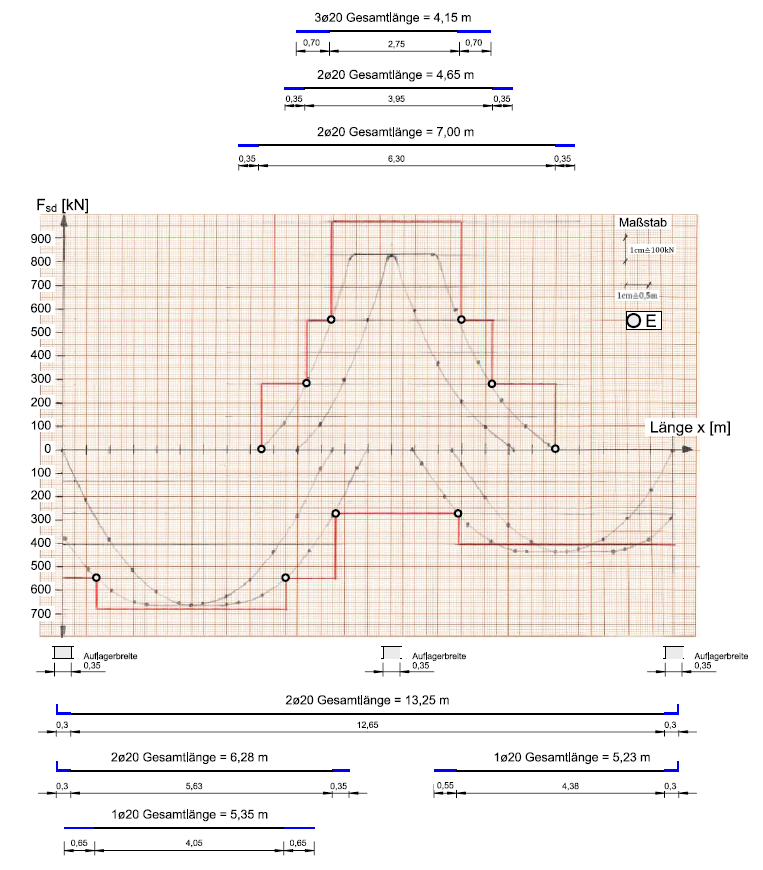
| − | :Vollständige Zugkraftdeckung „Stufenfunktion“ mit Auszug der Biegezugbewehrung. Die Verankerungslängen wurden blau gekennzeichnet und | + | ::Vollständige Zugkraftdeckung „Stufenfunktion“ mit Auszug der Biegezugbewehrung. Die Verankerungslängen wurden blau gekennzeichnet und beginnen ab dem rechnerischen Endpunkt. |
| − | [[Datei:Zugkraftdeckung (Bsp.) 16.png|mini|1000px|none|Vollständige Zugkraftdeckung „Stufenfunktion“]] | + | ::[[Datei:Zugkraftdeckung (Bsp.) 16.png|mini|1000px|none|Vollständige Zugkraftdeckung „Stufenfunktion“]] |
| + | <br> | ||
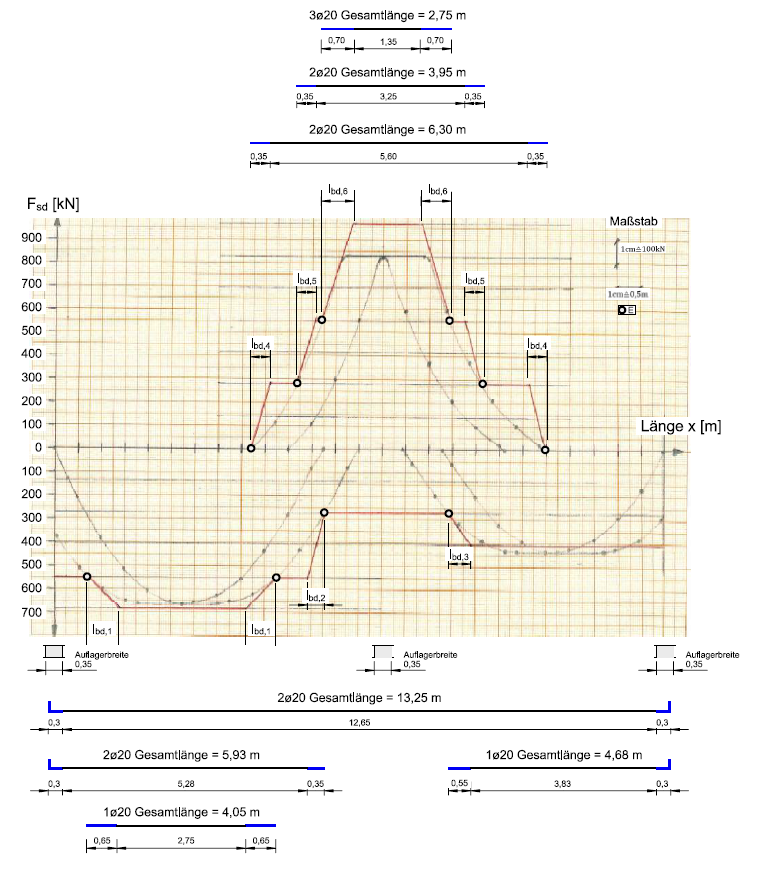
:*'''Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“''' | :*'''Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“''' | ||
| + | ::Vollständige Zugkraftdeckung „anschmiegende Funktion“ mit Auszug der Biegezugbewehrung. Die Verankerungslängen wurden blau gekennzeichnet. Der Abstand zwischen zwei rechnerischen Endpunkten entspricht der Gesamtlänge eines Stabes. | ||
| + | ::[[Datei:Zugkraftdeckung (Bsp.) 17.png|mini|1000px|none|Vollständige Zugkraftdeckung „anschmiegende Funktion“]] | ||
| + | ==Abschließende Betrachtung Berechnungsbeispiel - händisch== | ||
| + | Das Ergebnis der Zugkraftdeckung sind Länge und Position der abgestuften Bewehrungsstähle. Diese Parameter lassen sich direkt für die Stabstahlliste und den Bewehrungsplan verwenden. | ||
| − | + | Eine händische Durchführung kommt heutzutage oftmals nur noch zu Lehrzwecken zur Anwendung. Die händische grafische Durchführung ist verhältnismäßig aufwendig und erfordert viele unterschiedliche und voneinander abhängige Einzelschritte, um zu dem endgültigen Ergebnis zu gelangen. Das Verfahren ist hierdurch, je nach Bemessungsaufgabe, teilweise relativ schnell fehlerbehaftet. Wird die Zugkraftdeckung händisch auf Millimeterpapier vollzogen, ist dies generell mit leichten zeichnerischen Toleranzen verbunden. Auch beim Abmessen der Stablängen anhand der Zugkraftdeckungslinie können leichte Ungenauigkeiten entstehen. Dennoch lassen sich brauchbare Ergebnisse erzielen, welche mit denen einer Softwarebemessung vergleichbar sind. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Die händische grafische Durchführung ist verhältnismäßig aufwendig und erfordert viele unterschiedliche Einzelschritte um zu dem endgültigen Ergebnis zu gelangen. Das Verfahren ist hierdurch relativ schnell | ||
:'''Betrachtung der Varianten:''' | :'''Betrachtung der Varianten:''' | ||
| Zeile 322: | Zeile 375: | ||
::Zum Vergleich: | ::Zum Vergleich: | ||
::*Variante a - Zugkraftdeckungslinie „Stufenfunktion“ | ::*Variante a - Zugkraftdeckungslinie „Stufenfunktion“ | ||
| − | :::Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): 85,39 m Stabstahl ⌀20 | + | :::Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): '''85,39 m''' Stabstahl ⌀20 |
:::Dies entspricht einem Gewicht von 210,9 kg | :::Dies entspricht einem Gewicht von 210,9 kg | ||
::*Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“ | ::*Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“ | ||
| − | :::Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): 75,84 m Stabstahl ⌀20 | + | :::Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): '''75,84 m''' Stabstahl ⌀20 |
:::Dies entspricht einem Gewicht von 187,3 kg | :::Dies entspricht einem Gewicht von 187,3 kg | ||
| + | ::*Keine Zugkraftdeckung (Bewehrung nicht abgestuft) | ||
| + | :::Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): '''103,50 m''' Stabstahl ⌀20 | ||
| + | :::Dies entspricht einem Gewicht von 255,6 kg | ||
| + | |||
| + | |||
| + | ::Fazit: | ||
| − | + | ::Mit Variante b lässt sich im Vergleich zu Variante a grundsätzlich noch mehr Bewehrungsstahl einsparen. Am Betrachtungsbeispiel sind dies 23,6 kg. Das entspricht einer Einsparung von circa 11%. Nach aktuellem Handelspreis (März 2024; Angabe ohne Gewähr) würde sich für das betrachtete Bauteil daraus eine Einsparungssumme von etwa 30,00 € ergeben. | |
| − | + | ::Im Vergleich zu einer durchlaufenden, nicht abgestuften Bewehrungsführung ergibt sich durch Variante a eine Materialeinsparung von 17,5% und durch Variante b eine Einsparung von 26,7%. | |
=Berechnungsbeispiel Software mb-BauStatik= | =Berechnungsbeispiel Software mb-BauStatik= | ||
| − | Im Folgenden werden kommentierte Auszüge aus dem Berechnungsmodul „Stahlbeton-Durchlaufträger (S340.de) aus der mb-BauStatik-Software aufgeführt. Hierbei liegt der Fokus bei der Zusammenstellung der für die Zugkraftdeckung notwendigen Bemessungsinhalte. | + | Im Folgenden werden kommentierte Auszüge aus dem Berechnungsmodul „Stahlbeton-Durchlaufträger (S340.de)″ aus der mb-BauStatik-Software aufgeführt. Hierbei liegt der Fokus bei der Zusammenstellung der für die Zugkraftdeckung notwendigen Bemessungsinhalte. |
==Bemessung== | ==Bemessung== | ||
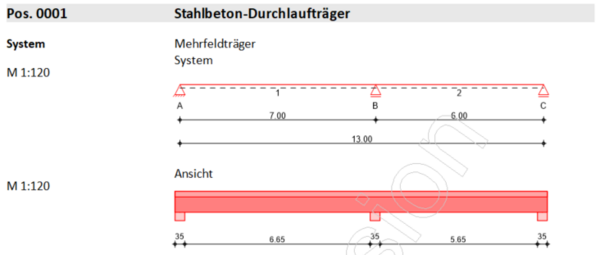
[[Datei:Zugkraftdeckung (Bsp.) mb 1.png|mini|600px|none|Statisches System und Bauteilansicht]] | [[Datei:Zugkraftdeckung (Bsp.) mb 1.png|mini|600px|none|Statisches System und Bauteilansicht]] | ||
| + | <br> | ||
| + | |||
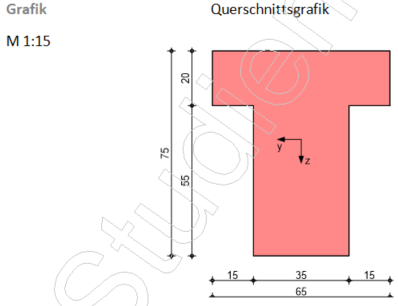
[[Datei:Zugkraftdeckung (Bsp.) mb 2.png|mini|600px|none|Bauteilquerschnitt ]] | [[Datei:Zugkraftdeckung (Bsp.) mb 2.png|mini|600px|none|Bauteilquerschnitt ]] | ||
| + | <br> | ||
| + | |||
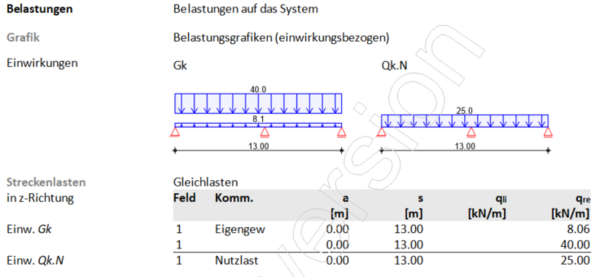
[[Datei:Zugkraftdeckung (Bsp.) mb 3.png|mini|600px|none|Belastungen auf das System]] | [[Datei:Zugkraftdeckung (Bsp.) mb 3.png|mini|600px|none|Belastungen auf das System]] | ||
| + | <br> | ||
| + | |||
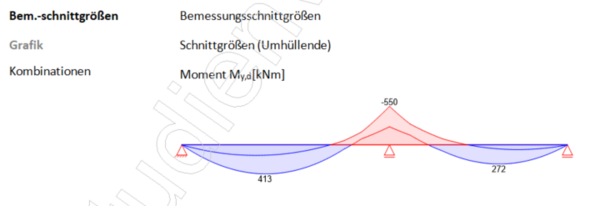
[[Datei:Zugkraftdeckung (Bsp.) mb 4.png|mini|600px|none|Momentengrenzlinie]] | [[Datei:Zugkraftdeckung (Bsp.) mb 4.png|mini|600px|none|Momentengrenzlinie]] | ||
| + | <br> | ||
| + | |||
[[Datei:Zugkraftdeckung (Bsp.) mb 5.png|mini|600px|none|Biegebemessung]] | [[Datei:Zugkraftdeckung (Bsp.) mb 5.png|mini|600px|none|Biegebemessung]] | ||
| + | <br> | ||
| + | |||
[[Datei:Zugkraftdeckung (Bsp.) mb 6.png|mini|600px|none|Querkraftbemessung (Druckstrebenneigungswinkel)]] | [[Datei:Zugkraftdeckung (Bsp.) mb 6.png|mini|600px|none|Querkraftbemessung (Druckstrebenneigungswinkel)]] | ||
| Zeile 345: | Zeile 414: | ||
Die Durchmesser der Längsbewehrung wurden ausschließlich auf 20 mm festgelegt. | Die Durchmesser der Längsbewehrung wurden ausschließlich auf 20 mm festgelegt. | ||
[[Datei:Zugkraftdeckung (Bsp.) mb 7.png|mini|600px|none|Durchmesser der Längsbewehrung]] | [[Datei:Zugkraftdeckung (Bsp.) mb 7.png|mini|600px|none|Durchmesser der Längsbewehrung]] | ||
| + | <br> | ||
| + | |||
Bei der Einstellung zur Staffelung wurde „unabhängige Staffelung“ gewählt. Hiermit konnte die Staffelung in etwa an die Abstufungsschritte aus der händischen Durchführung angepasst werden. Das manuelle vorgeben der Stufenzahl führte zu keinem brauchbaren Ergebnis, da sich nicht zwischen oberer und unterer Bewehrungslage differenzieren lässt. | Bei der Einstellung zur Staffelung wurde „unabhängige Staffelung“ gewählt. Hiermit konnte die Staffelung in etwa an die Abstufungsschritte aus der händischen Durchführung angepasst werden. Das manuelle vorgeben der Stufenzahl führte zu keinem brauchbaren Ergebnis, da sich nicht zwischen oberer und unterer Bewehrungslage differenzieren lässt. | ||
[[Datei:Zugkraftdeckung (Bsp.) mb 8.png|mini|600px|none|Staffelung]] | [[Datei:Zugkraftdeckung (Bsp.) mb 8.png|mini|600px|none|Staffelung]] | ||
| + | <br> | ||
| + | |||
Für das [[Versatzmaß]] ist das Abstandsmaß der vom Stegrand ausgelagerten Bewehrung relevant. Diesbezüglich lassen sich in der Software kein Informationen finden. Die Vergleichbarkeit zum händischen Berechnungsbeispiel ist hierbei somit nicht eindeutig möglich. Gewählt wurde „nach Norm“. | Für das [[Versatzmaß]] ist das Abstandsmaß der vom Stegrand ausgelagerten Bewehrung relevant. Diesbezüglich lassen sich in der Software kein Informationen finden. Die Vergleichbarkeit zum händischen Berechnungsbeispiel ist hierbei somit nicht eindeutig möglich. Gewählt wurde „nach Norm“. | ||
[[Datei:Zugkraftdeckung (Bsp.) mb 9.png|mini|600px|none|ausgelagerte Stützbewehrung]] | [[Datei:Zugkraftdeckung (Bsp.) mb 9.png|mini|600px|none|ausgelagerte Stützbewehrung]] | ||
| + | <br> | ||
| + | |||
Die Zuggurtkraftdifferenz soll über das Versatzmaß berücksichtigt werden. | Die Zuggurtkraftdifferenz soll über das Versatzmaß berücksichtigt werden. | ||
[[Datei:Zugkraftdeckung (Bsp.) mb 10.png|mini|600px|none|Variante zur Berücksichtigung der Zuggurtkraftdifferenz]] | [[Datei:Zugkraftdeckung (Bsp.) mb 10.png|mini|600px|none|Variante zur Berücksichtigung der Zuggurtkraftdifferenz]] | ||
| + | <br> | ||
| + | |||
In Berücksichtigung der konstruktiven Regeln zur Bewehrungsführung sollen mindestens 25% der Bewehrung zum Auflager geführt werden. | In Berücksichtigung der konstruktiven Regeln zur Bewehrungsführung sollen mindestens 25% der Bewehrung zum Auflager geführt werden. | ||
[[Datei:Zugkraftdeckung (Bsp.) mb 11.png|mini|600px|none|Steuerung der Längsbewehrung]] | [[Datei:Zugkraftdeckung (Bsp.) mb 11.png|mini|600px|none|Steuerung der Längsbewehrung]] | ||
| + | <br> | ||
==Zugkraftdeckung== | ==Zugkraftdeckung== | ||
| − | Als Ausgabe im Programm erhält man eine Zugkraftdeckungslinie mit den entsprechenden Bewehrungsauszügen. | + | Als Ausgabe im Programm erhält man eine Zugkraftdeckungslinie mit den entsprechenden Bewehrungsauszügen. Ermöglicht wird die Zugkraftdeckung in mb-BauStatik alleinig nach der Variante „Stufenfunktion“ (nach DIN 1045-1). |
| + | <br> | ||
Die Staffelung der oberen Längsbewehrung ließ sich aufgrund fehlender Einstellmöglichkeit nicht äquivalent zum händischen Berechnungsbeispiel wählen. | Die Staffelung der oberen Längsbewehrung ließ sich aufgrund fehlender Einstellmöglichkeit nicht äquivalent zum händischen Berechnungsbeispiel wählen. | ||
[[Datei:Zugkraftdeckung (Bsp.) mb 12.png|mini|600px|none|Zugkraftdeckungslinie]] | [[Datei:Zugkraftdeckung (Bsp.) mb 12.png|mini|600px|none|Zugkraftdeckungslinie]] | ||
| + | <br> | ||
| − | Bewehrungswahl in Tabellenform | + | Bewehrungswahl in Tabellenform: |
[[Datei:Zugkraftdeckung (Bsp.) mb 13.png|mini|600px|none|Bewehrungswahl (Biegezugbewehrung) ]] | [[Datei:Zugkraftdeckung (Bsp.) mb 13.png|mini|600px|none|Bewehrungswahl (Biegezugbewehrung) ]] | ||
| Zeile 384: | Zeile 464: | ||
[[Datei:Zugkraftdeckung (Bsp.) Harzer 5.png|mini|600px|none|Erforderliche Biegebewehrung]] | [[Datei:Zugkraftdeckung (Bsp.) Harzer 5.png|mini|600px|none|Erforderliche Biegebewehrung]] | ||
| + | <br> | ||
Die Durchmesser der Längsbewehrung wurden ausschließlich auf 20 mm festgelegt. | Die Durchmesser der Längsbewehrung wurden ausschließlich auf 20 mm festgelegt. | ||
| Zeile 392: | Zeile 473: | ||
==Zugkraftdeckung== | ==Zugkraftdeckung== | ||
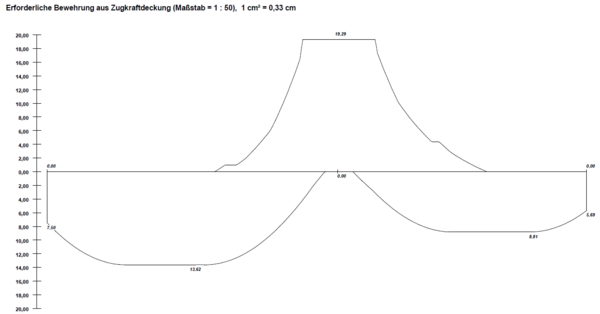
| − | Im Modul lässt sich keine Auswahl oder | + | Im Modul lässt sich keine Auswahl oder Einstellung zur Zugkraftdeckung treffen. Auf welche Weise die Zuggurtkraftdifferenz erfasst wird, bleibt unbekannt. |
[[Datei:Zugkraftdeckung (Bsp.) Harzer 8.png|mini|600px|none|Linie der erforderlichen Bewehrungsmenge]] | [[Datei:Zugkraftdeckung (Bsp.) Harzer 8.png|mini|600px|none|Linie der erforderlichen Bewehrungsmenge]] | ||
| + | <br> | ||
| − | Das Modul erstellt keine eigene Zugkraftdeckungslinie. Es gibt jedoch die Funktion, die Zugkraftlinie maßstäblich zu plotten. Hiermit kann die Zugkraftdeckung händisch oder durch Einlesen der Datei in externe Zeichenprogramme vollzogen werden. Die Skalierung der Ordinate entspricht dem Bewehrungsquerschnitt A<sub>s</sub> in cm<sup>2</sup>. | + | Das Modul erstellt keine eigene Zugkraftdeckungslinie. Es gibt jedoch die Funktion, die Zugkraftlinie maßstäblich zu plotten. Hiermit kann die Zugkraftdeckung händisch oder durch Einlesen der Datei in externe Zeichenprogramme vollzogen werden. Nach welcher Variante die Zugkraftdeckung hierbei vollzogen wird, bleibt dem Bearbeiter freigestellt. Die Skalierung der Ordinate entspricht dem Bewehrungsquerschnitt A<sub>s</sub> in cm<sup>2</sup>. |
[[Datei:Zugkraftdeckung (Bsp.) Harzer 9.png|mini|600px|none|Linie der erforderlichen Bewehrungsmenge (maßstäblicher Plot)]] | [[Datei:Zugkraftdeckung (Bsp.) Harzer 9.png|mini|600px|none|Linie der erforderlichen Bewehrungsmenge (maßstäblicher Plot)]] | ||
| + | <br> | ||
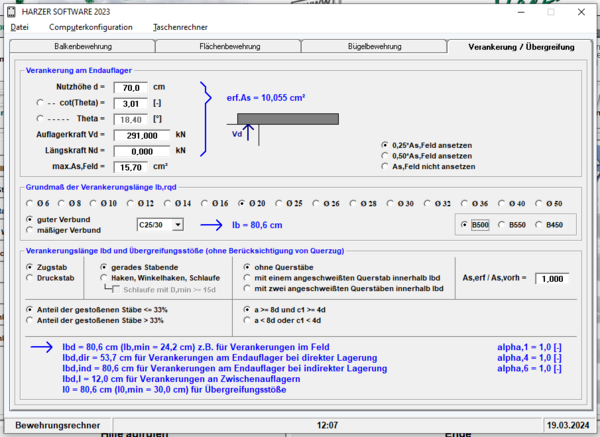
Die Verankerungslängen sind einzeln in einem gesonderten Modul zu bestimmen. Hierbei ist je nach gesuchter Verankerungslänge das Verhältnis aus A<sub>s,erf</sub> und A<sub>s,vorh</sub> einzutragen. | Die Verankerungslängen sind einzeln in einem gesonderten Modul zu bestimmen. Hierbei ist je nach gesuchter Verankerungslänge das Verhältnis aus A<sub>s,erf</sub> und A<sub>s,vorh</sub> einzutragen. | ||
[[Datei:Zugkraftdeckung (Bsp.) Harzer 10.png|mini|600px|none|Modul - Verankerungslänge]] | [[Datei:Zugkraftdeckung (Bsp.) Harzer 10.png|mini|600px|none|Modul - Verankerungslänge]] | ||
| + | <br> | ||
| + | |||
| + | '''Zugkraftdeckung:''' | ||
| + | |||
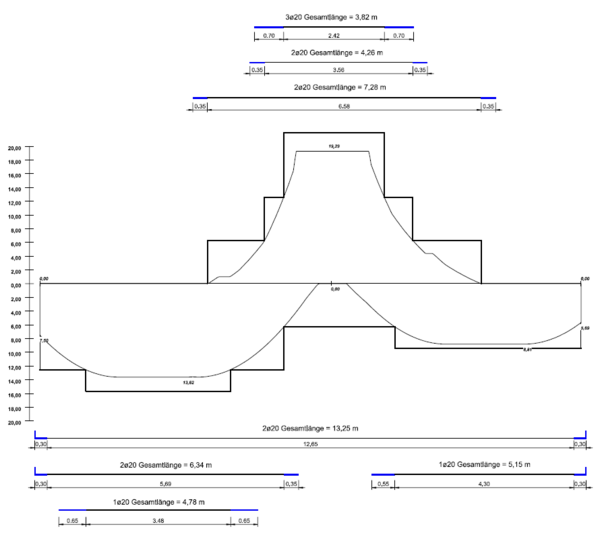
Die Verankerungslängen wurden separat in einem anderen Modul bestimmt. Die Abstufungsschritte wurden in Anlehnung an das händische Berechnungsbeispiel vorgenommen. Erstellt wurde die Zugkraftdeckungslinie mit einem externen Zeichenprogramm anhand des maßstäblichen Plot aus dem Berechnungsmodul. | Die Verankerungslängen wurden separat in einem anderen Modul bestimmt. Die Abstufungsschritte wurden in Anlehnung an das händische Berechnungsbeispiel vorgenommen. Erstellt wurde die Zugkraftdeckungslinie mit einem externen Zeichenprogramm anhand des maßstäblichen Plot aus dem Berechnungsmodul. | ||
| Zeile 405: | Zeile 492: | ||
=Vergleich der Berechnungsergebnisse= | =Vergleich der Berechnungsergebnisse= | ||
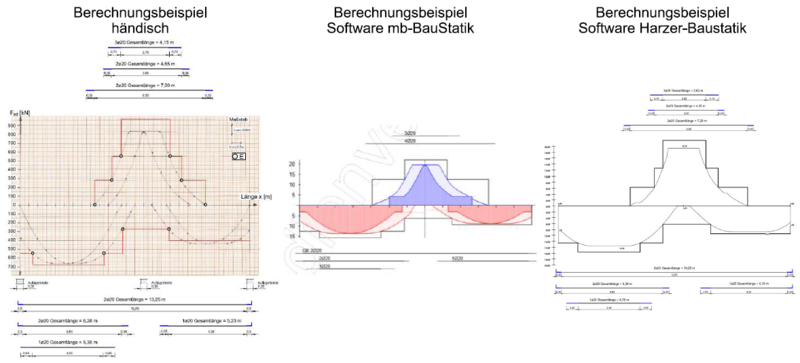
| − | [[Datei:Zugkraftdeckung (Bsp.) Vergleich 1.png|mini|800px|none|Zugkraftdeckungslinien]] | + | Verglichen werden kann folglich jeweils nur die Variante der Zugkraftdeckung als „Stufenfunktion“, da die Software mb-BauStatik ausschließlich diese Variante als Möglichkeit bietet. |
| + | [[Datei:Zugkraftdeckung (Bsp.) Vergleich 1.png|mini|800px|none|Zugkraftdeckungslinien der verschiedenen Berechnungen]] | ||
| + | <br> | ||
| + | |||
Ergebnis der Zugkraftdeckung sind die Stablängen der abgestuften Bewehrungsstähle. Diese werden anhand der Zugkraftdeckungslinie ermittelt. Die Zugkraftdeckungslinie richtet sich nach dem Verlauf der Stahlzugkraft F<sub>s</sub> (Zugkraftlinie). Im Falle der Softwarebemessung erfolgt die Zugkraftdeckung anhand der Linie der erforderliche Biegezugbewehrung. Beides lässt sich aufgrund der Äquivalenz der Verläufe trotzdem miteinander vergleichen. Bei der händischen Berechnung sind der gesamte Berechnungsablauf und die dafür Verwendeten Eingangswerte schrittweise veranschaulicht und somit direkt nachvollziehbar. Bei der Softwarebemessung hingegen bleiben die Berechnungsansätze der Zugkraftdeckung weitestgehend unbekannt und sind nicht ohne weiteres einsehbar. | Ergebnis der Zugkraftdeckung sind die Stablängen der abgestuften Bewehrungsstähle. Diese werden anhand der Zugkraftdeckungslinie ermittelt. Die Zugkraftdeckungslinie richtet sich nach dem Verlauf der Stahlzugkraft F<sub>s</sub> (Zugkraftlinie). Im Falle der Softwarebemessung erfolgt die Zugkraftdeckung anhand der Linie der erforderliche Biegezugbewehrung. Beides lässt sich aufgrund der Äquivalenz der Verläufe trotzdem miteinander vergleichen. Bei der händischen Berechnung sind der gesamte Berechnungsablauf und die dafür Verwendeten Eingangswerte schrittweise veranschaulicht und somit direkt nachvollziehbar. Bei der Softwarebemessung hingegen bleiben die Berechnungsansätze der Zugkraftdeckung weitestgehend unbekannt und sind nicht ohne weiteres einsehbar. | ||
| + | <br> | ||
In folgender Tabelle sind die Stab- und Verankerungslängen der abgestuften Bewehrungsstähle aufgelistet: | In folgender Tabelle sind die Stab- und Verankerungslängen der abgestuften Bewehrungsstähle aufgelistet: | ||
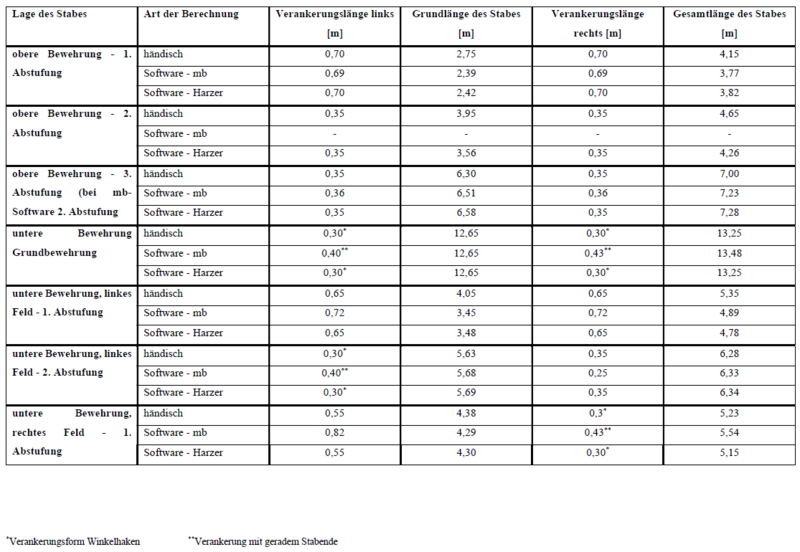
| − | [[Datei:Zugkraftdeckung (Bsp.) Vergleich 2.png|mini|800px|none| | + | [[Datei:Zugkraftdeckung (Bsp.) Vergleich 2.png|mini|800px|none|Stablängen der Berechnungsvarianten]] |
| + | <br> | ||
| − | Für den Vergleich zwischen den Berechnungsarten ist die Grundlänge der Stäbe am aussagekräftigsten. Hierbei lässt sich feststellen, dass die Stab – Grundlängen aus den beiden Softwarebemessungen nahezu identisch sind. Somit ist anzunehmen, das hierbei gleiche Berechnungsansätze zur Anwendung kamen. Die aus der händischen Zugkraftdeckung ermittelten Stablängen sind zumeist eher größer, | + | Für den Vergleich zwischen den Berechnungsarten ist die Grundlänge der Stäbe am aussagekräftigsten. Hierbei lässt sich feststellen, dass die Stab – Grundlängen aus den beiden Softwarebemessungen nahezu identisch sind. Somit ist anzunehmen, das hierbei gleiche Berechnungsansätze zur Anwendung kamen. Die aus der händischen Zugkraftdeckung ermittelten Stablängen sind zumeist eher größer, vereinzelt aber auch etwas kleiner als die Längen aus der Softwarebemessung. |
| − | *'''Mögliche Ursachen für Unterschiede:''' | + | *'''Mögliche Ursachen für Unterschiede bei den Stablängen:''' |
:Da die Grundlängen der Stäbe aus den Softwareanwendungen nahezu identisch sind, ist generell die Abweichung im Vergleich zur Handrechnung zu Betrachten. | :Da die Grundlängen der Stäbe aus den Softwareanwendungen nahezu identisch sind, ist generell die Abweichung im Vergleich zur Handrechnung zu Betrachten. | ||
| − | :Die verwendeten Druckstrebenneigungswinkel sind bei allen drei Berechnungen einsehbar und nahezu gleich. Unter der Annahme | + | :Die verwendeten Druckstrebenneigungswinkel sind bei allen drei Berechnungen einsehbar und nahezu gleich. Unter der Annahme deren Verwendung in Verbindung mit der Zugkraftdeckung können die Differenzen hieraus nicht resultieren. |
| − | :Die Berücksichtigung der Zuggurtkraftdifferenz erfolgt sowohl bei der mb Software, als auch bei der Handrechnung über das Versatzmaß a<sub>l</sub>. Dieses errechnet sich unter anderem aus dem Hebelarm der inneren Kräfte z. Bei der Handrechnung wurde das Versatzmaß vereinfacht zu 0,9 · d bestimmt. Die Größe der verwendeten Versatzmaße lassen sich in den Softwares nicht einsehen. Unter der Annahme, das dort zum Bestimmen der Versatzmaße die genaueren Werte für z aus der Biegebemessung verwendet wurden, würden sich größere Versatzmaße und somit größere Stablängen als bei der Handrechnung ergeben. Daher sind die Abweichungen der Stablängen | + | :Die Berücksichtigung der Zuggurtkraftdifferenz erfolgt sowohl bei der mb Software, als auch bei der Handrechnung über das Versatzmaß a<sub>l</sub>. Dieses errechnet sich unter anderem aus dem Hebelarm der inneren Kräfte z. Bei der Handrechnung wurde das Versatzmaß vereinfacht zu 0,9 · d bestimmt. Die Größe der verwendeten Versatzmaße lassen sich in den Softwares nicht einsehen. Unter der Annahme, das dort zum Bestimmen der Versatzmaße die genaueren Werte für z aus der Biegebemessung verwendet wurden, würden sich größere Versatzmaße und somit größere Stablängen als bei der Handrechnung ergeben. Daher sind die Abweichungen der Stablängen höchstwahrscheinlich nicht auf das Versatzmaß zurückzuführen. Ebenfalls ist bei den Softwareberechnungen nicht einsehbar in wieweit das Maß der ausgelagerten Bewehrung bei der oberen Bewehrung am Plattenbalken berücksichtigt wurde. Dieses spielt bei der Größe des Versatzmaßes ebenfalls eine Rolle. |
:Die ermittelten Verankerungslängen sind bei der Handrechnung identisch mit den Werten aus der Harzer-Software. Bei den in der mb-Software ermittelten Verankerungslängen sind teilweise etwas höhere Abweichungen zu den Werten der anderen beiden Vergleichsberechnungen festzustellen. Zurückzuführen ist dies vermutlich auf den Berechnungsansatz zur Ermittlung der Stahlspannungen am Verankerungsbeginn. | :Die ermittelten Verankerungslängen sind bei der Handrechnung identisch mit den Werten aus der Harzer-Software. Bei den in der mb-Software ermittelten Verankerungslängen sind teilweise etwas höhere Abweichungen zu den Werten der anderen beiden Vergleichsberechnungen festzustellen. Zurückzuführen ist dies vermutlich auf den Berechnungsansatz zur Ermittlung der Stahlspannungen am Verankerungsbeginn. | ||
| − | :Die Verankerungslängen am Endauflager sind bei der mb-Software für ein gerades Stabende angegeben. Die Software verweist hierbei darauf, das eine gesonderte Verankerungsform zu wählen ist. | + | :Die Verankerungslängen am Endauflager sind bei der mb-Software für ein gerades Stabende angegeben. Die Software verweist hierbei darauf, das eine gesonderte Verankerungsform zu wählen ist. Somit sind die Verankerungslängen am Endauflager nicht direkt miteinander vergleichbar, da bei den anderen beiden Berechnungsarten bereits die Verankerung mit Winkelhaken berücksichtigt wurde und damit die Länge der Verankerung entsprechend kürzer ist. |
| − | :Als wohl maßgebendste Ursache für die Unterschiede in den Stablängen ist die Zugkraftlinie bzw. Linie der erforderlichen Bewehrung in Betracht zu ziehen. Grundlage für die Zugkraftlinie ist bei den drei Berechnungsvarianten jeweils die gleiche Momentengrenzlinie. Aus der Momentengrenzlinie wird über den Hebelarm der inneren Kräfte z die Zugkraftlinie bestimmt. Bei der Handrechnung erfolgte dies mit der auf der sicheren Seite liegenden Annahme z = 0,9 · d. In der Softwarebemessung wurde hierfür sehr wahrscheinlich der genaue Wert für z verwendet. Da dieser im Regelfall größer als bei der vereinfachten Annahme z = 0,9 | + | :Als wohl maßgebendste Ursache für die Unterschiede in den Stablängen ist die Zugkraftlinie bzw. Linie der erforderlichen Bewehrung in Betracht zu ziehen. Grundlage für die Zugkraftlinie ist bei den drei Berechnungsvarianten jeweils die gleiche Momentengrenzlinie. Aus der Momentengrenzlinie wird über den Hebelarm der inneren Kräfte z die Zugkraftlinie bestimmt. Bei der Handrechnung erfolgte dies mit der auf der sicheren Seite liegenden Annahme z = 0,9 · d. In der Softwarebemessung wurde hierfür sehr wahrscheinlich der genaue Wert für z verwendet. Da dieser im Regelfall größer als bei der vereinfachten Annahme z = 0,9 · d ausfällt, führt dies zu einer rechnerisch etwas geringeren Zugkraft. Das heißt, die Zugkraftlinie fällt damit kleiner aus. Hieraus resultieren dann kürzere Stablängen. Gut erkennbar ist dieser Unterschied an den Abständen der Zugkraftlinien zum Bewerhrungshorizont der größten Stabanzahl. Die Bewehrungshorizonte sind in allen Berechnungsvarianten auf der gleichen Ebene. Vergleicht man daraufhin die Abstände der Zugkraftlinien an den Extremstellen zum Bewehrungshorizont, ist festzustellen, dass die Zugkraftline der Handrechnung größer ausfällt. |
| − | Ebenfalls können Zeichen- oder Messungenauigkeiten bei der händischen Durchführung der Zugkraftdeckung zu den Abweichungen der Stablängen beitragen. | + | :Ebenfalls können Zeichen- oder Messungenauigkeiten bei der händischen Durchführung der Zugkraftdeckung zu den Abweichungen der Stablängen beitragen. |
*'''Schlussfolgerungen:''' | *'''Schlussfolgerungen:''' | ||
| − | : | + | :Die ermittelten Stablängen der einzelnen Varianten bewegen sich neben geringfügigen Abweichungen alle in einer ähnlichen Größenordnung. Somit liegt die Zugkraftdeckung bei keiner der betrachteten Varianten besonders verstärkt auf der sicheren Seite. Für Bewehrungskonstruktionen im Stahlbetonbau sind die Längenabweichungen überwiegend unverhältnismäßig und eher von untergeordneter Bedeutung. Generell bietet die betrachtete Zugkraftdeckung als „Stufenfunktion“ (nach DIN 1045-1) ein gewisses Maß an Sicherheiten zum Ausgleichen von kleineren Abweichungen. Schadensfälle durch eine vermeidlich zu unpräzise Zugkraftdeckung sind eher unwahrscheinlich. |
| − | + | ||
| + | :Schlussendlich wird jede der 3 betrachteten Varianten den Bestimmungen aus der Norm gerecht. Demzufolge ist das Durchführen der Zugkraftdeckung mit den vorgestellten Varianten problemlos möglich und die Auswahl des Verfahrens bleibt dem Anwender überlassen. | ||
| + | |||
=weitere Seiten zum Thema Zugkraftdeckung= | =weitere Seiten zum Thema Zugkraftdeckung= | ||
| Zeile 436: | Zeile 530: | ||
[[Versatzmaß]] | [[Versatzmaß]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | =Quellen= | ||
| + | |||
| + | <references /> | ||
| + | |||
| + | |||
| + | {{Seiteninfo | ||
| + | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | ||
| + | |Status = Seite fertig, ungeprüft | ||
| + | }} | ||
[[Kategorie:Beispiele-Stahlbetonbau]] | [[Kategorie:Beispiele-Stahlbetonbau]] | ||
Aktuelle Version vom 29. April 2024, 17:09 Uhr
Folglich wird ein praxisnahes Berechnungsbeispiel zum Thema Zugkraftdeckung geführt. Dieses wird vergleichsweise händisch und mit zwei verschiedenen Bemessungssoftwares geführt.
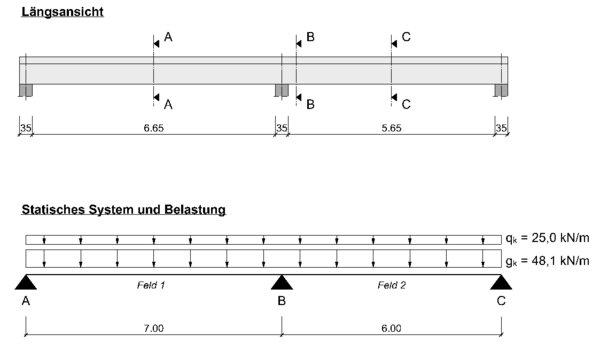
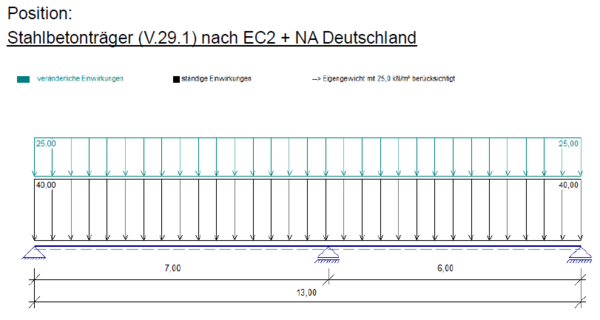
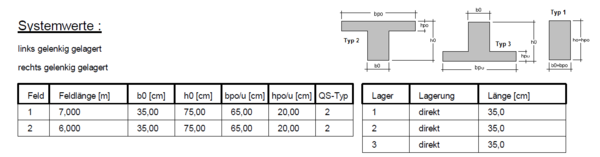
Statisches System und Belastung
Betrachtet wird ein Durchlaufträger mit 2 Feldern unterschiedlicher Spannweite. Es handelt sich um einen Plattenbalkenquerschnitt, welcher frei drehbar gelagert ist.
Betongüte: C25/30
Betonstabstahl: B500A
Berechnungsbeispiel - händisch
Nachfolgend wird schrittweise die grafische händische Durchführung der Zugkraftdeckung an einem praxisnahen Berechnungsbeispiel erläutert. Hierbei werden auch die beiden Varianten hinsichtlich des Ansatzes der Tragfähigkeit der Bewehrung in der Verankerungslänge gegenübergestellt.
Grundlagen
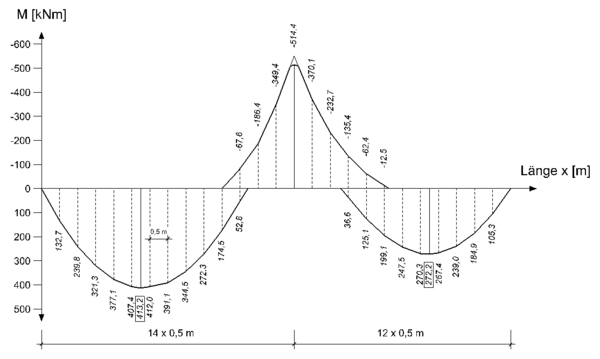
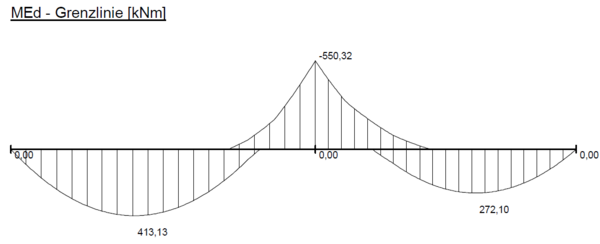
- Momentengrenzlinie
- Grundlage ist die Momentengrenzline (Bemessungswerte), welche aufgrund der verschiedenen Möglichkeiten der Laststellungen geeignet zu bestimmen ist (z.B. Schnittprinzip).
- Um die Zugkraftdeckung zeichnerisch durchzuführen, sind schrittweise einzelne Werte des Verlaufes der Momentengrenzlinie zu bestimmen. Die Schrittweite ist so zu wählen, dass der Verlauf entsprechend „feinfühlig“ dargestellt wird. Im Falle des Beispiels führt ein Abstand von 0,5m zu einem zufriedenstellenden Ergebnis. Mit der Annahme der Anwendung des Schnittprinzips ist also alle 0,5m entlang der Systemlänge der Bemessungswert des Biegemomentes zu bestimmen. Aufgrund der Lagerungsbedingung am Zwischenauflager darf das Stützmoment abgemindert werden (Momentenausrundung). Dies ist ebenfalls zu berücksichtigen.
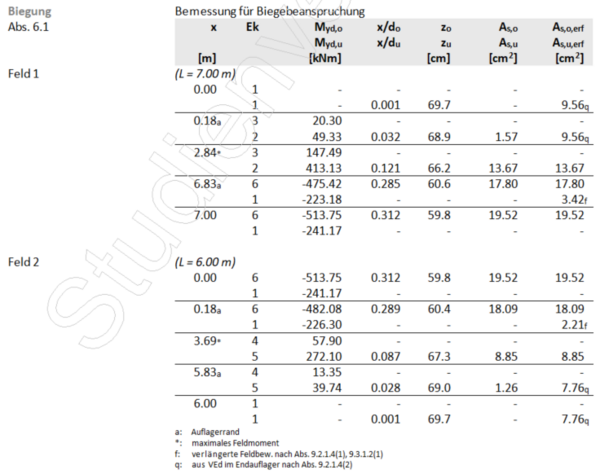
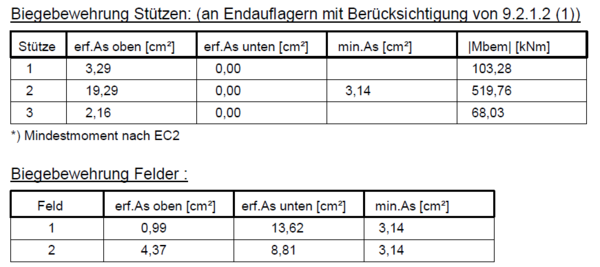
- Ergebnisse aus der Biege- und Querkraftbemessung
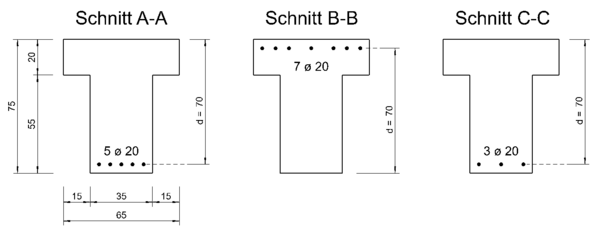
- Aus der Biegebemessung ist Anzahl, Durchmesser und Stahlgüte der Längsbewehrung bekannt.
- Der Querschnitt des Plattenbalkens wird mit der gewählten Bewehrungsmenge und deren Anordnung am entsprechenden Betrachtungsschnitt (Querkraftbewehrung nicht dargestellt) in nachfolgender Grafik veranschaulicht. Auch die statische Nutzhöhe (d) lässt sich aus der Grafik entnehmen. Aufgrund der einlagigen Anordnung ist diese im Beispiel stets 70 cm.
- Ebenfalls sind die Druckstrebenneigungswinkel aus der bereits vollzogenen Querkraftbemessung bekannt:
- Am Auflager A und C ist θ = 18,4°→ cot θ = 3,00
- Am Auflager B links ist θ = 25,0°→ cot θ = 2,14
- Am Auflager B rechts ist θ = 22,9°→ cot θ = 2,37
- Der Neigungswinkel der Bügelbewehrung beträgt α = 90° →cot α = 0
- Die Bemessungswerte der Querkräfte an den Endauflagern betragen bei Auflager A = 290,99 kN und bei B = 236,05 kN.
Bestimmen der M/z - Linie (Zugkraft aufgrund von Biegemomenten)
Die M/z Linie lässt sich aus der Momentengrenzline bestimmen. Ziel ist es, den Verlauf der Stahlzugkraft Fsd aufgrund von Biegemomenten in Diagrammform darzustellen. Um die entsprechenden Werte für das Zugkraftdiagramm zu erhalten, ist jeder einzelne Bemessungswert aus der Momentengrenzlinie durch den Hebelarm der inneren Kräfte (z) zu dividieren. Man erhält somit aus dem Moment MEd [kNm] die Stahlzugkraft Fsd [kN].
Die Stahlzugkraft Fsd errechnet sich somit zu:[1]
MEd... Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie) z... Der Hebelarm der inneren Kräfte errechnet sich im Falle des Beispiels aus der statischen Nutzhöhe zu 0,9 · d. NEd... Bemessungswert des einwirkenden Normalkraft (keine einwirkende Normalkraft vorhanden→ entfällt somit)
Aufgrund des sich immer wiederholenden Berechnungsschrittes wird dieser folglich nur einmal exemplarisch am maximalen Biegemoment in Feld 1 veranschaulicht:
Nach dieser Vorgehensweise sind alle Werte aus der Momentengrenzlinie in die entsprechende Stahlzugkraft umzurechnen. Eine Tabelle kann hierfür sehr sinnvoll sein:
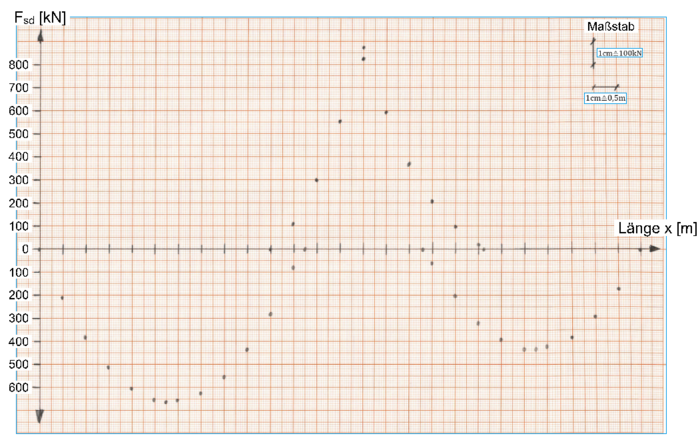
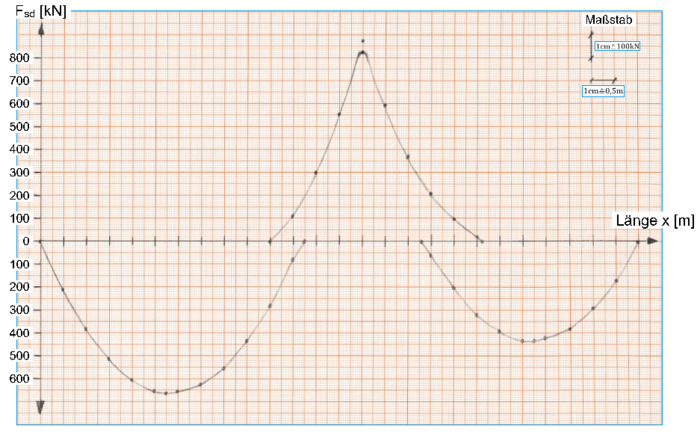
Sind alle Werte bestimmt, lassen sich diese anhand ihrer Koordinaten im Zugkraftdiagramm eintragen. Bei der händischen Durchführung eignet sich hierfür Millimeterpapier. Die Maßstäbe können hierbei frei gewählt werden.
Sind alle Punkte im Diagramm eingetragen, lassen sich diese entsprechend verbinden, um den Zugkraftverlauf zu erhalten.
Fsd – Linie (Zugkraft aufgrund von Biegemomenten und Querkraft)
Um den tatsächlichen Verlauf der Stahlzugkraft aufgrund von Biegemoment und Querkraft im Zugkraftdiagramm darzustellen, ist die Zuggurtkraftdifferenz zu berücksichtigen. Bei der zeichnerischen Durchführung erfolgt dies durch horizontales Versetzen der M/z – Linie um das Versatzmaß al.
Das Versatzmaß al ergibt sich zu:[1]
cot θ... Druckstrebenneigungswinkel cot α... Neigungswinkel der Bügelbewehrung z... Der Hebelarm der inneren Kräfte errechnet sich im Falle des Beispiels aus der statischen Nutzhöhe zu 0,9 · d.
Aufgrund der unterschiedlichen Druckstrebenneigungswinkel pro Bemessungsabschnitt, ist das Versatzmaß für das betrachtete Beispiel mehrfach zu bestimmen.
Der Hebelarm der inneren Kräfte bleibt auf gesamter Bauteillänge konstant und ergibt sich zu:
Der Neigungswinkel der Bügelbewehrung beträgt α = 90° →cot α = 0
Am Auflager A und C ist cot θ = 3,00
Somit ergibt sich das Versatzmaß zu:
Zu beachten:
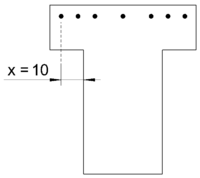
Am Zwischenauflager (Auflager B) ist die obere Biegezugbewehrung teilweise aus dem Stegbereich in die Gurtplatte ausgelagert. Hier ist das Versatzmaß um den Abstand der vom Stegrand am weitesten ausgelagerten Bewehrung zu vergrößern (Maß x).
Am Auflager B links ist cot θ = 2,14
Somit ergibt sich das Versatzmaß entsprechend der Lage der Bewehrung zu:
- obere Bewehrung:
- untere Bewehrung:
Am Auflager B rechts ist cot θ = 2,37
Somit ergibt sich das Versatzmaß entsprechend der Lage der Bewehrung zu:
- obere Bewehrung:
- untere Bewehrung:
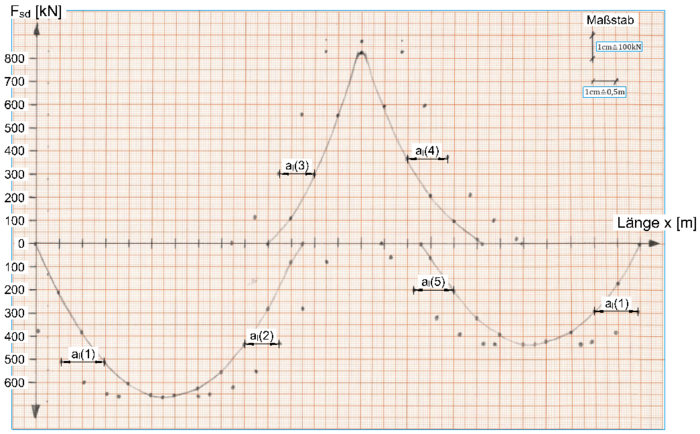
Mit den ermittelten Versatzmaßen lassen sich die zuvor im Zugkraftdiagramm ermittelten Punkte horizontal verschieben. Zu beachten ist, dass das jeweils korrekte Versatzmaß an entsprechender Stelle verwendet wird. Hierbei sind die Auflagerlinien und die Extremstellen im Diagramm als Orientierungspunkte für die Anwendung des entsprechenden Versatzmaßes anzusehen. Versetzt wird jeweils immer nach „außen“.
Sind alle versetzten Punkte im Diagramm eingetragen, lassen sich diese entsprechend verbinden, um den endgültigen Zugkraftverlauf zu erhalten. Optisch deutlich erkennbar ist nun, dass die Zugkraftlinien horizontal um das Versatzmaß parallelverschoben sind.
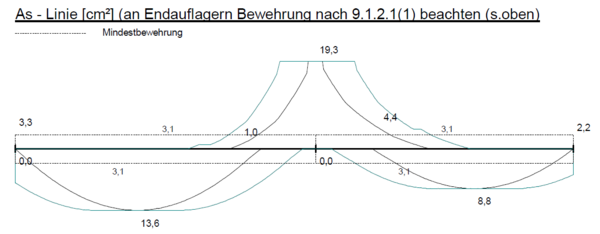
Eintragen der Bewehrungshorizonte
Aus der bereits vollzogenen Biegebemessung sind Durchmesser und Anzahl der Bewehrungsstäbe als Biegezugbewehrung bekannt. Jeder einzelne Stab kann aufgrund seiner Querschnittsfläche und der Stahlfestigkeit eine entsprechende Zugkraft F⌀ aufnehmen.
Die pro Bewehrungsstahl aufnehmbare Zugkraft F⌀ errechnet sich zu:[1]
As⌀... Querschnittsfläche des Bewehrungsstahls fyd... Bemessungswert der Stahlstreckgrenze
Verbaut werden Bewehrungsstähle B500A mit einem Durchmesser von 20 mm.
Daraus ergibt sich eine Querschnittsfläche von As⌀ = 3,14 cm2 und ein Bemessungswert der Festigkeit von fyd = 43,5 kN/cm2 .
Die aufnehmbare Zugkraft pro Bewehrungsstahl berechnet sich somit zu:
Mit zunehmender Anzahl der Bewehrungsstähle kann kontinuierlich mehr Zugkraft aufgenommen werden. In nachfolgender Tabelle wurde die Zugkraft entsprechend der Stabanzahl aufsummiert.
Im Zugkraftdiagramm sind entsprechend der aufnehmbaren Zugkraft die einzelnen Bewehrungsstähle als sogenannte „Bewehrungshorizonte“ als feine Orientierungslinien einzutragen.
Auszug aus Feld 2: Die durch 3 Bewehrungsstähle aufnehmbare Zugkraft unterschreitet offensichtlich geringfügig die mit der Zugkraftlinie dargestellte einwirkende Zugkraft. Diese geringe Abweichung ist jedoch akzeptabel. Zurückzuführen ist dies auf den Hebelarm der inneren Kräfte (z). Die Biegebemessung und damit die Bewehrungswahl erfolgt mit dem exakten Wert für z. Die Zugkraftlinie hingegen wird auf der sicheren Seite liegend vereinfacht mit z = 0,9 · d bestimmt. Hierdurch wird im Zugkraftdiagramm eine teilweise etwas höhere Stahlzugkraft dargestellt als tatsächlich auftreten wird.
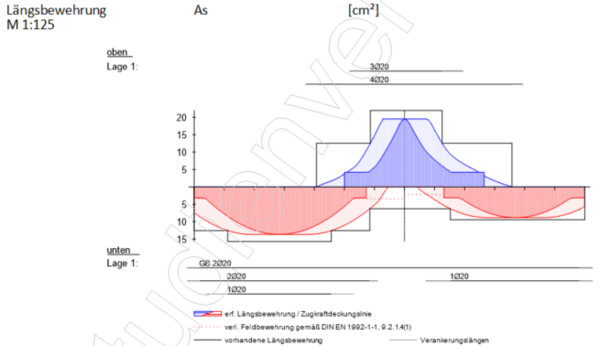
Zugkraftdeckungslinie (Abstufen der Biegezugbewehrung)
Betrachtet werden beide Varianten der Zugkraftdeckungslinie.
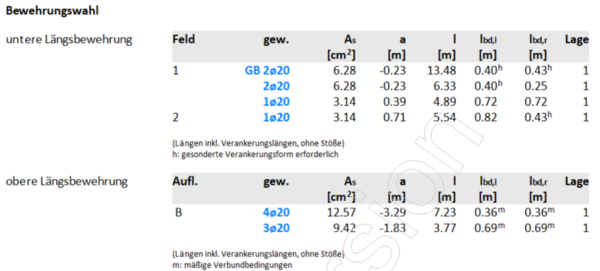
Abgestuft wird wie folgt:
- Untere Bewehrung:
- 2 Stäbe laufen ohne Abstufung auf gesamter Länge durch
- Auflager A → insgesamt 4 Stäbe werden ins Auflager geführt, 1 Stab wird vorher abgestuft
- Auflager B links → abgestuft werden 1x 2 Stäbe und 1x 1 Stab
- Auflager B rechts → abgestuft wird 1 x 1 Stab
- Auflager C → alle 3 Stäbe aus Feld 2 werden ins Auflager geführt
- Obere Bewehrung:
- abgestuft werden 2 x 2 Stäbe und 1 x 3 Stäbe
Variante a - Zugkraftdeckungslinie „Stufenfunktion“ (nach DIN 1045-1)
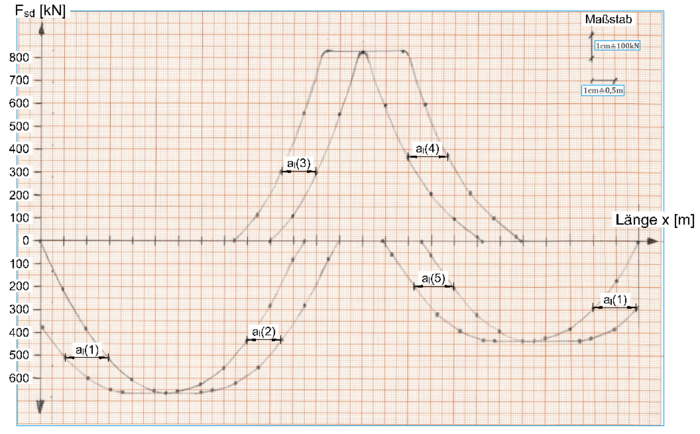
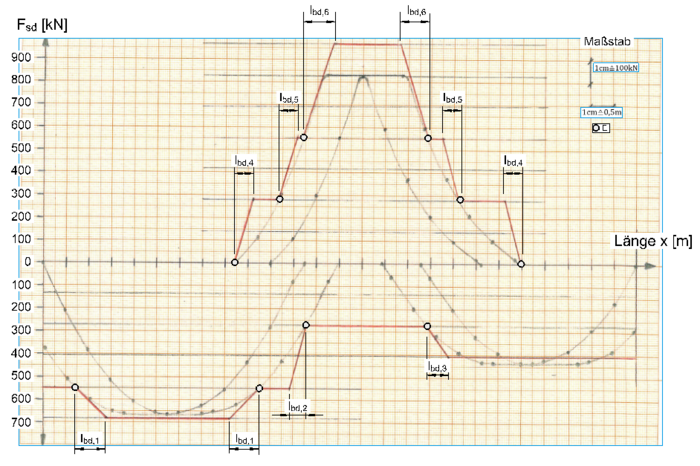
Vollständige Zugkraftdeckungslinie „Stufenfunktion“ (rote Linie):
Orientierungspunkte beim Zeichnen sind die Bewehrungshorizonte und die rechnerischen Endpunkten E der Bewehrung. Abstufungsschritte wie vorab beschrieben.
Bestimmen der Verankerungslängen (Zwischenschritt)
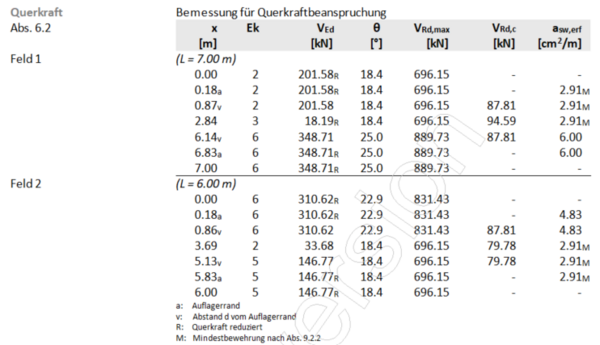
Für beide Varianten der Zugkraftdeckung sind die Maße der Verankerungslängen erforderlich. Bei Variante b) werden die Verankerungslängen bereits beim Zeichnen der Zugkraftdeckungslinie benötigt. Exemplarisch wird das Errechnen der erforderlichen Verankerungslänge an 2 verschiedenen Positionen veranschaulicht. Am Zwischenauflager läuft die nicht abgestufte untere Bewehrung durch. Der Nachweis der Verankerungslänge entfällt hier somit.
Verankerung am Endauflager[1]
- Ermitteln der Randzugkraft FEd (Zugkraft am Endauflager):
VEd... entspricht dem Bemessungswert der maximalen Auflagerkraft al... Versatzmaß aus Zugkraftdeckung z... Hebelarm der inneren Kräfte NEd... Bemessungswert der einwirkenden Normalkraft
-
- Maßgebend: 436,50 kN
- Ermitteln, des zur Aufnahme der Randzugkraft erforderlichen Bewehrungsquerschnitt
fyd... Bemessungswert der Stahlstreckgrenze
- Ermitteln der Stahlspannung
As,vorh... Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe
- 4⌀20 werden bis ins Auflager geführt
- Hieraus errechnet sich die vorhandene Querschnittsfläche:
- Somit errechnet sich die Stahlspannung zu:
- Grundwert der Verankerungslänge
- Guter Verbund (Bewehrung liegt unten), für Beton C25/30 ist somit fbd = 2,69 N/mm2
fbd... Verbundfestigkeit ⌀s... Stabdurchmesser
- Bemessungswert der Verankerungslänge
- Beiwerte:
- -Verankerung mit Winkelhaken → α1=0,7
- (Aufgrund der begrenzten Platzverhältnisse zur Verankerung am Endauflager musste die Verankerungsform Winkelhaken gewählt werden)
- -Keine angeschweißten Querstäbe → α4=1,0
- -direkte Lagerung → α5=2/3
- Mindestwert der Verankerungslänge
- → Mindestverankerungslänge wird nicht maßgebend
- Nachweis:
- Unter der Annahme einer Betondeckung von cnom = 5 cm werden die Bewehrungsstähle auf gesamter Auflagerbreite mit Winkelhaken verankert.
- → Nachweis erfüllt
Verankerung außerhalb von Auflagern[1]
Verankerung der unteren Bewehrung in Feld 1:
- Ermittlung der Stahlspannung am rechnerischen Endpunkt E
- Hierbei ist das Verhältnis aus erforderlicher und vorhandener Bewehrung zu bilden.
- 2 Stäbe werden noch gebraucht
- 4 Stäbe sind vorhanden
- Somit ist:
- As,erf=6,28cm2 (2⌀20)
- As,vorh=12,56cm2 (5⌀20)
As,vorh... Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe
- Die Stahlspannung errechnet sich zu:
- Grundwert der Verankerungslänge
- Guter Verbund (Bewehrung liegt unten), für Beton C25/30 ist somit fbd = 2,69 N/mm2
fbd... Verbundfestigkeit ⌀s... Stabdurchmesser
- Bemessungswert der Verankerungslänge
- Beiwerte:
- -Verankerung mit geradem Stabende → α1=1,0
- -Keine angeschweißten Querstäbe → α4=1,0
- -keine Querdruck- oder Querzugspannungen → α5=1,0
- Mindestwert der Verankerungslänge
- → Mindestverankerungslänge wird nicht Maßgebend
- Nachweis:
- gewählte Verankerungslänge → 45 cm
- → Nachweis erfüllt
Nach dieser Vorgehensweise sind die Verankerungen aller Stabenden nachzuweisen.
→ Mit den errechneten Verankerungslängen lässt sich folglich nun auch die Zugkraftdeckungslinie für Variante b erstellen
Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“
Für diese Variante sind die Verankerungslängen bereits vor dem Zeichnen der Zugkraftdeckungslinie anhand der Abstufungsschritte zu ermitteln.
Vollständige Zugkraftdeckungslinie „anschmiegende Funktion“ (rote Linie):
Orientierungspunkte beim Zeichnen sind die Bewehrungshorizonte und die rechnerischen Endpunkten E der Bewehrung. Die Bereiche mit linearen Verlauf lassen sich über die entsprechende Verankerungslänge konstruieren. Abstufungsschritte wie eingangs beschrieben.
Bewehrungslängen ermitteln
Über den gewählten Maßstab lassen sich anhand der Zugkraftdeckungslinie die tatsächlichen Stablängen und deren Position im Bauteil ermitteln. Die Verankerungslängen sind hierbei stets zu berücksichtigen. Zu beachten ist bei der Längenermittlung ebenfalls die Auflagerbreite der Endauflager. Denn das Zugkraftdiagramm bezieht sich nur auf die Abstände der rechnerischen Auflagerlinien.
- Variante a - Zugkraftdeckungslinie „Stufenfunktion“
- Vollständige Zugkraftdeckung „Stufenfunktion“ mit Auszug der Biegezugbewehrung. Die Verankerungslängen wurden blau gekennzeichnet und beginnen ab dem rechnerischen Endpunkt.
- Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“
- Vollständige Zugkraftdeckung „anschmiegende Funktion“ mit Auszug der Biegezugbewehrung. Die Verankerungslängen wurden blau gekennzeichnet. Der Abstand zwischen zwei rechnerischen Endpunkten entspricht der Gesamtlänge eines Stabes.
Abschließende Betrachtung Berechnungsbeispiel - händisch
Das Ergebnis der Zugkraftdeckung sind Länge und Position der abgestuften Bewehrungsstähle. Diese Parameter lassen sich direkt für die Stabstahlliste und den Bewehrungsplan verwenden.
Eine händische Durchführung kommt heutzutage oftmals nur noch zu Lehrzwecken zur Anwendung. Die händische grafische Durchführung ist verhältnismäßig aufwendig und erfordert viele unterschiedliche und voneinander abhängige Einzelschritte, um zu dem endgültigen Ergebnis zu gelangen. Das Verfahren ist hierdurch, je nach Bemessungsaufgabe, teilweise relativ schnell fehlerbehaftet. Wird die Zugkraftdeckung händisch auf Millimeterpapier vollzogen, ist dies generell mit leichten zeichnerischen Toleranzen verbunden. Auch beim Abmessen der Stablängen anhand der Zugkraftdeckungslinie können leichte Ungenauigkeiten entstehen. Dennoch lassen sich brauchbare Ergebnisse erzielen, welche mit denen einer Softwarebemessung vergleichbar sind.
- Betrachtung der Varianten:
- Mit dem grafischen Verfahren lassen sich beide Varianten der Zugkraftdeckung vollziehen. Beide Varianten ergeben aufgrund ihrer Unterschiede bezüglich des Ansatzes der Tragfähigkeit in der Verankerungslänge unterschiedliche Bewehrungslängen.
- Zum Vergleich:
- Variante a - Zugkraftdeckungslinie „Stufenfunktion“
- Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): 85,39 m Stabstahl ⌀20
- Dies entspricht einem Gewicht von 210,9 kg
- Variante b - Zugkraftdeckungslinie „anschmiegende Funktion“
- Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): 75,84 m Stabstahl ⌀20
- Dies entspricht einem Gewicht von 187,3 kg
- Keine Zugkraftdeckung (Bewehrung nicht abgestuft)
- Erforderliche Menge an Bewehrungsstahl (Längsbewehrung): 103,50 m Stabstahl ⌀20
- Dies entspricht einem Gewicht von 255,6 kg
- Zum Vergleich:
- Fazit:
- Mit Variante b lässt sich im Vergleich zu Variante a grundsätzlich noch mehr Bewehrungsstahl einsparen. Am Betrachtungsbeispiel sind dies 23,6 kg. Das entspricht einer Einsparung von circa 11%. Nach aktuellem Handelspreis (März 2024; Angabe ohne Gewähr) würde sich für das betrachtete Bauteil daraus eine Einsparungssumme von etwa 30,00 € ergeben.
- Im Vergleich zu einer durchlaufenden, nicht abgestuften Bewehrungsführung ergibt sich durch Variante a eine Materialeinsparung von 17,5% und durch Variante b eine Einsparung von 26,7%.
Berechnungsbeispiel Software mb-BauStatik
Im Folgenden werden kommentierte Auszüge aus dem Berechnungsmodul „Stahlbeton-Durchlaufträger (S340.de)″ aus der mb-BauStatik-Software aufgeführt. Hierbei liegt der Fokus bei der Zusammenstellung der für die Zugkraftdeckung notwendigen Bemessungsinhalte.
Bemessung
Erläuterung Auswahl - und Einstellungsmöglichkeiten zur Zugkraftdeckung
Die Durchmesser der Längsbewehrung wurden ausschließlich auf 20 mm festgelegt.
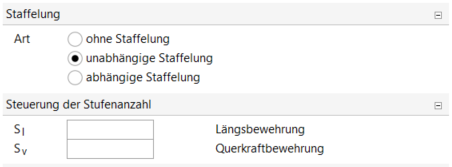
Bei der Einstellung zur Staffelung wurde „unabhängige Staffelung“ gewählt. Hiermit konnte die Staffelung in etwa an die Abstufungsschritte aus der händischen Durchführung angepasst werden. Das manuelle vorgeben der Stufenzahl führte zu keinem brauchbaren Ergebnis, da sich nicht zwischen oberer und unterer Bewehrungslage differenzieren lässt.
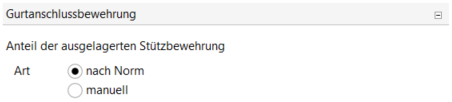
Für das Versatzmaß ist das Abstandsmaß der vom Stegrand ausgelagerten Bewehrung relevant. Diesbezüglich lassen sich in der Software kein Informationen finden. Die Vergleichbarkeit zum händischen Berechnungsbeispiel ist hierbei somit nicht eindeutig möglich. Gewählt wurde „nach Norm“.
Die Zuggurtkraftdifferenz soll über das Versatzmaß berücksichtigt werden.
In Berücksichtigung der konstruktiven Regeln zur Bewehrungsführung sollen mindestens 25% der Bewehrung zum Auflager geführt werden.
Zugkraftdeckung
Als Ausgabe im Programm erhält man eine Zugkraftdeckungslinie mit den entsprechenden Bewehrungsauszügen. Ermöglicht wird die Zugkraftdeckung in mb-BauStatik alleinig nach der Variante „Stufenfunktion“ (nach DIN 1045-1).
Die Staffelung der oberen Längsbewehrung ließ sich aufgrund fehlender Einstellmöglichkeit nicht äquivalent zum händischen Berechnungsbeispiel wählen.
Bewehrungswahl in Tabellenform:
Berechnungsbeispiel Software Harzer-Baustatik
Im Folgenden werden kommentierte Auszüge aus dem Berechnungsmodul „Stahlbetonträger“ aus der Software Harzer-Baustatik aufgeführt. Hierbei liegt der Fokus bei der Zusammenstellung der für die Zugkraftdeckung notwendigen Bemessungsinhalte.
Bemessung
Die Durchmesser der Längsbewehrung wurden ausschließlich auf 20 mm festgelegt.
Zugkraftdeckung
Im Modul lässt sich keine Auswahl oder Einstellung zur Zugkraftdeckung treffen. Auf welche Weise die Zuggurtkraftdifferenz erfasst wird, bleibt unbekannt.
Das Modul erstellt keine eigene Zugkraftdeckungslinie. Es gibt jedoch die Funktion, die Zugkraftlinie maßstäblich zu plotten. Hiermit kann die Zugkraftdeckung händisch oder durch Einlesen der Datei in externe Zeichenprogramme vollzogen werden. Nach welcher Variante die Zugkraftdeckung hierbei vollzogen wird, bleibt dem Bearbeiter freigestellt. Die Skalierung der Ordinate entspricht dem Bewehrungsquerschnitt As in cm2.
Die Verankerungslängen sind einzeln in einem gesonderten Modul zu bestimmen. Hierbei ist je nach gesuchter Verankerungslänge das Verhältnis aus As,erf und As,vorh einzutragen.
Zugkraftdeckung:
Die Verankerungslängen wurden separat in einem anderen Modul bestimmt. Die Abstufungsschritte wurden in Anlehnung an das händische Berechnungsbeispiel vorgenommen. Erstellt wurde die Zugkraftdeckungslinie mit einem externen Zeichenprogramm anhand des maßstäblichen Plot aus dem Berechnungsmodul.
Vergleich der Berechnungsergebnisse
Verglichen werden kann folglich jeweils nur die Variante der Zugkraftdeckung als „Stufenfunktion“, da die Software mb-BauStatik ausschließlich diese Variante als Möglichkeit bietet.
Ergebnis der Zugkraftdeckung sind die Stablängen der abgestuften Bewehrungsstähle. Diese werden anhand der Zugkraftdeckungslinie ermittelt. Die Zugkraftdeckungslinie richtet sich nach dem Verlauf der Stahlzugkraft Fs (Zugkraftlinie). Im Falle der Softwarebemessung erfolgt die Zugkraftdeckung anhand der Linie der erforderliche Biegezugbewehrung. Beides lässt sich aufgrund der Äquivalenz der Verläufe trotzdem miteinander vergleichen. Bei der händischen Berechnung sind der gesamte Berechnungsablauf und die dafür Verwendeten Eingangswerte schrittweise veranschaulicht und somit direkt nachvollziehbar. Bei der Softwarebemessung hingegen bleiben die Berechnungsansätze der Zugkraftdeckung weitestgehend unbekannt und sind nicht ohne weiteres einsehbar.
In folgender Tabelle sind die Stab- und Verankerungslängen der abgestuften Bewehrungsstähle aufgelistet:
Für den Vergleich zwischen den Berechnungsarten ist die Grundlänge der Stäbe am aussagekräftigsten. Hierbei lässt sich feststellen, dass die Stab – Grundlängen aus den beiden Softwarebemessungen nahezu identisch sind. Somit ist anzunehmen, das hierbei gleiche Berechnungsansätze zur Anwendung kamen. Die aus der händischen Zugkraftdeckung ermittelten Stablängen sind zumeist eher größer, vereinzelt aber auch etwas kleiner als die Längen aus der Softwarebemessung.
- Mögliche Ursachen für Unterschiede bei den Stablängen:
- Da die Grundlängen der Stäbe aus den Softwareanwendungen nahezu identisch sind, ist generell die Abweichung im Vergleich zur Handrechnung zu Betrachten.
- Die verwendeten Druckstrebenneigungswinkel sind bei allen drei Berechnungen einsehbar und nahezu gleich. Unter der Annahme deren Verwendung in Verbindung mit der Zugkraftdeckung können die Differenzen hieraus nicht resultieren.
- Die Berücksichtigung der Zuggurtkraftdifferenz erfolgt sowohl bei der mb Software, als auch bei der Handrechnung über das Versatzmaß al. Dieses errechnet sich unter anderem aus dem Hebelarm der inneren Kräfte z. Bei der Handrechnung wurde das Versatzmaß vereinfacht zu 0,9 · d bestimmt. Die Größe der verwendeten Versatzmaße lassen sich in den Softwares nicht einsehen. Unter der Annahme, das dort zum Bestimmen der Versatzmaße die genaueren Werte für z aus der Biegebemessung verwendet wurden, würden sich größere Versatzmaße und somit größere Stablängen als bei der Handrechnung ergeben. Daher sind die Abweichungen der Stablängen höchstwahrscheinlich nicht auf das Versatzmaß zurückzuführen. Ebenfalls ist bei den Softwareberechnungen nicht einsehbar in wieweit das Maß der ausgelagerten Bewehrung bei der oberen Bewehrung am Plattenbalken berücksichtigt wurde. Dieses spielt bei der Größe des Versatzmaßes ebenfalls eine Rolle.
- Die ermittelten Verankerungslängen sind bei der Handrechnung identisch mit den Werten aus der Harzer-Software. Bei den in der mb-Software ermittelten Verankerungslängen sind teilweise etwas höhere Abweichungen zu den Werten der anderen beiden Vergleichsberechnungen festzustellen. Zurückzuführen ist dies vermutlich auf den Berechnungsansatz zur Ermittlung der Stahlspannungen am Verankerungsbeginn.
- Die Verankerungslängen am Endauflager sind bei der mb-Software für ein gerades Stabende angegeben. Die Software verweist hierbei darauf, das eine gesonderte Verankerungsform zu wählen ist. Somit sind die Verankerungslängen am Endauflager nicht direkt miteinander vergleichbar, da bei den anderen beiden Berechnungsarten bereits die Verankerung mit Winkelhaken berücksichtigt wurde und damit die Länge der Verankerung entsprechend kürzer ist.
- Als wohl maßgebendste Ursache für die Unterschiede in den Stablängen ist die Zugkraftlinie bzw. Linie der erforderlichen Bewehrung in Betracht zu ziehen. Grundlage für die Zugkraftlinie ist bei den drei Berechnungsvarianten jeweils die gleiche Momentengrenzlinie. Aus der Momentengrenzlinie wird über den Hebelarm der inneren Kräfte z die Zugkraftlinie bestimmt. Bei der Handrechnung erfolgte dies mit der auf der sicheren Seite liegenden Annahme z = 0,9 · d. In der Softwarebemessung wurde hierfür sehr wahrscheinlich der genaue Wert für z verwendet. Da dieser im Regelfall größer als bei der vereinfachten Annahme z = 0,9 · d ausfällt, führt dies zu einer rechnerisch etwas geringeren Zugkraft. Das heißt, die Zugkraftlinie fällt damit kleiner aus. Hieraus resultieren dann kürzere Stablängen. Gut erkennbar ist dieser Unterschied an den Abständen der Zugkraftlinien zum Bewerhrungshorizont der größten Stabanzahl. Die Bewehrungshorizonte sind in allen Berechnungsvarianten auf der gleichen Ebene. Vergleicht man daraufhin die Abstände der Zugkraftlinien an den Extremstellen zum Bewehrungshorizont, ist festzustellen, dass die Zugkraftline der Handrechnung größer ausfällt.
- Ebenfalls können Zeichen- oder Messungenauigkeiten bei der händischen Durchführung der Zugkraftdeckung zu den Abweichungen der Stablängen beitragen.
- Schlussfolgerungen:
- Die ermittelten Stablängen der einzelnen Varianten bewegen sich neben geringfügigen Abweichungen alle in einer ähnlichen Größenordnung. Somit liegt die Zugkraftdeckung bei keiner der betrachteten Varianten besonders verstärkt auf der sicheren Seite. Für Bewehrungskonstruktionen im Stahlbetonbau sind die Längenabweichungen überwiegend unverhältnismäßig und eher von untergeordneter Bedeutung. Generell bietet die betrachtete Zugkraftdeckung als „Stufenfunktion“ (nach DIN 1045-1) ein gewisses Maß an Sicherheiten zum Ausgleichen von kleineren Abweichungen. Schadensfälle durch eine vermeidlich zu unpräzise Zugkraftdeckung sind eher unwahrscheinlich.
- Schlussendlich wird jede der 3 betrachteten Varianten den Bestimmungen aus der Norm gerecht. Demzufolge ist das Durchführen der Zugkraftdeckung mit den vorgestellten Varianten problemlos möglich und die Auswahl des Verfahrens bleibt dem Anwender überlassen.
weitere Seiten zum Thema Zugkraftdeckung
Quellen
Seiteninfo
|