Verankerung am Endauflager (Bsp.): Unterschied zwischen den Versionen
Gbolle (Diskussion | Beiträge) |
EWill (Diskussion | Beiträge) K |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Endauflager eines Plattenbalkens nachzuweisen. Allgemeine Regeln zur [https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php/Verankerungsl%C3%A4nge Verankerungslänge] und spezielle Hinweise zum Endauflager werden auf einer gesonderten Seite dargestellt. | |
| − | |||
| − | |||
| − | |||
| − | In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Endauflager eines Plattenbalkens nachzuweisen. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zum Endauflager | ||
== Aufgabenstellung == | == Aufgabenstellung == | ||
| Zeile 18: | Zeile 14: | ||
* Betonstabstahl: B500B | * Betonstabstahl: B500B | ||
* <math> cot \theta = 2,09 ; cot \alpha = 0</math> | * <math> cot \theta = 2,09 ; cot \alpha = 0</math> | ||
| − | * Von der Zugbewehrung werden 5 Stäbe bis zum | + | * Von der Zugbewehrung werden 5 Stäbe bis zum Endauflager geführt. |
| + | * Auflagerkraft <math>A_Ed=303,24kN</math> | ||
| + | * Betondeckung <math>c_v=5cm</math> | ||
== Lösung == | == Lösung == | ||
| Zeile 32: | Zeile 30: | ||
<math>z = 0,9 \cdot d = 0,9 \cdot 62,5 cm = 56,25 cm</math> | <math>z = 0,9 \cdot d = 0,9 \cdot 62,5 cm = 56,25 cm</math> | ||
| − | <math>a_L = z \cdot (cot {\theta} - cot {\alpha}) = 56,25 cm \cdot (2,09 - 0) = 58,8 cm</math> | + | <math>a_L = z \cdot (cot {\theta} - cot {\alpha})/2 = 56,25 cm \cdot (2,09 - 0)/2 = 58,8 cm</math> |
=== Randzugkraft === | === Randzugkraft === | ||
| Zeile 64: | Zeile 62: | ||
Angeschweißte Querstäbe: Keine → <math>{\alpha}_4 = 1,0</math> | Angeschweißte Querstäbe: Keine → <math>{\alpha}_4 = 1,0</math> | ||
| − | Querdruck: Aus Auflagerkraft → <math>{\alpha}_5 = 2/3</math> | + | Querdruck: Aus Auflagerkraft (direkte Lagerung) → <math>{\alpha}_5 = 2/3</math> |
| − | <math>l_{b,eq} = 1,0 \cdot 1,0 \cdot 2/3 \cdot 33,21 cm = \ | + | <math>l_{b,eq} = 1,0 \cdot 1,0 \cdot 2/3 \cdot 33,21 cm = \underline{\underline{22,14 cm}}</math> |
=== Mindestverankerungslänge === | === Mindestverankerungslänge === | ||
| Zeile 74: | Zeile 72: | ||
<math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 2/3 \cdot \left( \frac{2,0 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,304 kN/cm^2} \right) \\ 10 \cdot 2/3 \cdot 2,0 cm \end{matrix}} \right\} </math> | <math>l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 2/3 \cdot \left( \frac{2,0 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,304 kN/cm^2} \right) \\ 10 \cdot 2/3 \cdot 2,0 cm \end{matrix}} \right\} </math> | ||
| − | <math>l_{b,min} = max\left\{ {\begin{matrix} 14,31 cm \\ 13,33 cm \end{matrix}} \right\} </math> | + | <math>l_{b,min} = max\left\{ {\begin{matrix} 14,31 cm \\ 13,33 cm \end{matrix}} \right\} </math> |
| + | |||
| + | Im Übrigen gilt bei Endauflagern, dass die Bewehrung mindestens übder das rechnerische Auflager zu führen ist: | ||
| + | |||
| + | <math>l_{b,min}=15cm</math> | ||
| + | |||
| + | <math>\Rightarrow</math> Die Mindestverankerungslänge sit nicht maßgebend. | ||
=== Nachweis der Verankerungslänge === | === Nachweis der Verankerungslänge === | ||
| Zeile 80: | Zeile 84: | ||
<math>l_{b,vorh} = t - c_v = 30 cm - 5 cm = 25 cm</math> | <math>l_{b,vorh} = t - c_v = 30 cm - 5 cm = 25 cm</math> | ||
| − | <math>l_{b,vorh} = 25 cm \, \geq 22,14 cm = l_{b,eq}</math> | + | <math>\underline{\underline{l_{b,vorh} = 25 cm \, \geq 22,14 cm = l_{b,eq}}}</math> |
| Zeile 86: | Zeile 90: | ||
Dieses Beispiel berechnet die Verankerungslänge an einem Bereich des Systems. Zur umfassenden Bemessung muss die Verankerungslänge auch an anderen Stellen ermittelt werden, hierzu werden am Berechnungsbeispiel auch die Verankerungslänge am [[Verankerung am Zwischenauflager (Bsp.)|Zwischenauflager]], [[Verankerung außerhalb von Auflagern (Bsp.)|außerhalb von Auflagern]] und am [[Verankerung am Kragarmende (Bsp.)|Kragarmende]] bestimmt. | Dieses Beispiel berechnet die Verankerungslänge an einem Bereich des Systems. Zur umfassenden Bemessung muss die Verankerungslänge auch an anderen Stellen ermittelt werden, hierzu werden am Berechnungsbeispiel auch die Verankerungslänge am [[Verankerung am Zwischenauflager (Bsp.)|Zwischenauflager]], [[Verankerung außerhalb von Auflagern (Bsp.)|außerhalb von Auflagern]] und am [[Verankerung am Kragarmende (Bsp.)|Kragarmende]] bestimmt. | ||
| + | |||
| + | {{Seiteninfo | ||
| + | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | ||
| + | |Status = Seite fertig, ungeprüft | ||
| + | }} | ||
| + | |||
| + | |||
| + | [[Kategorie:Beispiele-Stahlbetonbau]] | ||
Aktuelle Version vom 13. Mai 2024, 20:34 Uhr
In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Endauflager eines Plattenbalkens nachzuweisen. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zum Endauflager werden auf einer gesonderten Seite dargestellt.
Aufgabenstellung
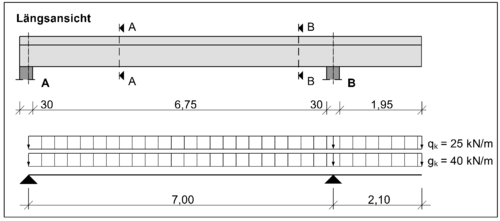
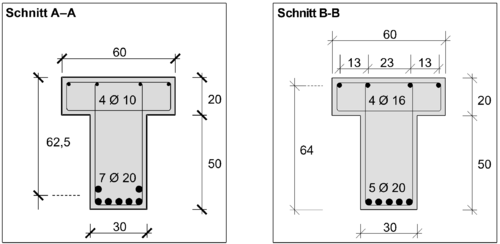
Für den dargestellten Plattenbalken soll die Verankerungslänge der Zugbewehrung am Endauflager bestimmt werden.
Folgende Daten sind gegeben:
- Beton: C30/37
- Betonstabstahl: B500B
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cot \theta = 2,09 ; cot \alpha = 0}
- Von der Zugbewehrung werden 5 Stäbe bis zum Endauflager geführt.
- Auflagerkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_Ed=303,24kN}
- Betondeckung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_v=5cm}
Lösung
Verbundfestigkeit
Bewehrung unten → guter Verbund
→ C30/37 → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{bd} = 3,04 N/mm^2 = 0,304 kN/cm^2}
Versatzmaß
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z = 0,9 \cdot d = 0,9 \cdot 62,5 cm = 56,25 cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_L = z \cdot (cot {\theta} - cot {\alpha})/2 = 56,25 cm \cdot (2,09 - 0)/2 = 58,8 cm}
Randzugkraft
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = V_{Ed} \cdot \frac{a_L}{z} + N_{Ed} = 303,24 kN \cdot \frac{58,8 cm}{56,25 cm} + 0 kN = 316,97 kN}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = 316,97 kN \, {\geq} \, \frac{V_{Ed}}{2} = \frac{303,24 kN}{2} = 151,62 kN}
Erforderliche Bewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = \frac{F_{sd}}{f_{yd}} = \frac{316,97 kN}{43,5kN/cm^2} = 7,29 cm^2}
Vorhandene Bewehrung
5 Ø 20 → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 15,71 cm^2}
Stahlspannung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5 kN/cm^2 \cdot \frac{7,29 cm^2}{15,71 cm^2} = 20,19 kN/cm^2}
Grundwert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}} = \frac{2,0 cm}{4} \cdot \frac{20,19 kN/cm^2}{0,304 kN/cm^2} = 33,21 cm}
Ersatzverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
Formgebung: Gerades Stabende → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 1,0}
Angeschweißte Querstäbe: Keine → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_4 = 1,0}
Querdruck: Aus Auflagerkraft (direkte Lagerung) → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5 = 2/3}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 1,0 \cdot 1,0 \cdot 2/3 \cdot 33,21 cm = \underline{\underline{22,14 cm}}}
Mindestverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 2/3 \cdot \left( \frac{2,0 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,304 kN/cm^2} \right) \\ 10 \cdot 2/3 \cdot 2,0 cm \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 14,31 cm \\ 13,33 cm \end{matrix}} \right\} }
Im Übrigen gilt bei Endauflagern, dass die Bewehrung mindestens übder das rechnerische Auflager zu führen ist:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min}=15cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Rightarrow} Die Mindestverankerungslänge sit nicht maßgebend.
Nachweis der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,vorh} = t - c_v = 30 cm - 5 cm = 25 cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\underline{l_{b,vorh} = 25 cm \, \geq 22,14 cm = l_{b,eq}}}}
Einordnung in die Gesamtbemessung der Verankerungslänge
Dieses Beispiel berechnet die Verankerungslänge an einem Bereich des Systems. Zur umfassenden Bemessung muss die Verankerungslänge auch an anderen Stellen ermittelt werden, hierzu werden am Berechnungsbeispiel auch die Verankerungslänge am Zwischenauflager, außerhalb von Auflagern und am Kragarmende bestimmt.
Seiteninfo
|