Mitwirkung des Betons zwischen den Rissen (Zugversteifung): Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Als Mitwirkung des Betons zwischen den Rissen (auch Zugversteifung bzw. engl. "tension stiffing") wird der Effekt bezeichnet, dass die Stahlspannungen zwischen…“) |
EWill (Diskussion | Beiträge) K |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Als Mitwirkung des Betons zwischen den Rissen (auch Zugversteifung bzw. engl. "tension | + | Als Mitwirkung des Betons zwischen den Rissen (auch Zugversteifung bzw. engl. "tension stiffening") wird der Effekt bezeichnet, dass die Stahlspannungen und somit auch die Stahlspannungen zwischen den Rissen abnehmen. Die Mitwirkung des Betons zwischen den Rissen beeinflusst maßgeblich die Steifigkeit des Bauteils im Zustand II. |
<br /> | <br /> | ||
| + | |||
| + | [[File:Mitwirkung_des_Betons_zwischen_den_Rissen_(Zugversteifung)_1.jpg|right|thumb|300px|Dehnungen bei abgeschlossener Rissbildung<ref name="zilch06">Zilch,K., Zehetmaier,G.: Bemessung im konstruktiven Betonbau; 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006</ref>]] | ||
=Allgemeines= | =Allgemeines= | ||
| Zeile 6: | Zeile 8: | ||
Grund für die Abnahme der Stahldehnungen zwischen den Rissen ist der Verbund zwischen Stahl und Beton. Im Riss ist kein Verbund zwischen Stahl und Beton mehr vorhanden, die Stahlspannung ist hier maximal. Zwischen den Rissen findet durch den Verbund von Stahl und Beton eine Kraftübertragung zwischen beiden Materialien statt; der Beton nimmt zwischen den Rissen ebenfalls Zugspannungen auf, sodass die Stahlspannung und -dehnung hier abnehmen. Mittig zwischen den Rissen wird die Stahlspannung minimal. | Grund für die Abnahme der Stahldehnungen zwischen den Rissen ist der Verbund zwischen Stahl und Beton. Im Riss ist kein Verbund zwischen Stahl und Beton mehr vorhanden, die Stahlspannung ist hier maximal. Zwischen den Rissen findet durch den Verbund von Stahl und Beton eine Kraftübertragung zwischen beiden Materialien statt; der Beton nimmt zwischen den Rissen ebenfalls Zugspannungen auf, sodass die Stahlspannung und -dehnung hier abnehmen. Mittig zwischen den Rissen wird die Stahlspannung minimal. | ||
| − | Durch die Abnahme der Dehnungen zwischen den Rissen nimmt die Bauteilsteifigkeit im Vergleich zum | + | Durch die Abnahme der Dehnungen zwischen den Rissen nimmt die Bauteilsteifigkeit im Vergleich zum reinen Zustand II zu. Dieser Effekt lässt sich anschaulich an den Krümmungen veranschaulichen, welche gemäß den Grundsätzen der Mechanik mit der Steifigkeit direkt zusammenhängen. Im Folgenden wird dies am Beispiel des Biegebalkens dargestellt. |
| + | |||
| + | Betrachtet man die folgenden Gleichungen und setzt voraus, dass Moment und statische Nutzhöhe gleichbleiben, führt die Verringerung der Stahldehnung zu einer Vergrößerung der Biegesteifigkeit. | ||
| + | |||
| + | <math>\kappa=\frac{M}{EI}=\frac{|\varepsilon_s|+|\varepsilon_c|}{d}</math> | ||
| − | + | <math>EI^{II}_r=\frac{M\cdot d}{|\varepsilon_{s2}|+|\varepsilon_c|}</math> | |
| − | + | <math>EI^{II}_m=\frac{M\cdot d}{|\varepsilon_{sm}|+|\varepsilon_c|}</math> | |
| − | + | wenn gilt <math>\varepsilon_{s2}>\varepsilon_{sm}</math> dann gilt ebenfalls <math>EI^{II}_r>EI^{II}_m</math> | |
| − | Abhängig vom Nachweis kann die Zugversteifung einen positiven oder negativen Einfluss auf das Nachweisergebnis haben. Beim Verformungsnachweis hat sie einen positiven Einfluss, da durch die höhere Steifigkeit die Verformungen abnehmen. Auf die Rotationsfähigkeit hat die Mitwirkung des Betons zwischen den Rissen einen negativen Einfluss, da durch die maximalen Stahldehnungen nicht in allen Bereichen voll aktiviert werden können. | + | wobei: |
| + | :{| | ||
| + | |- | ||
| + | | <math> \kappa </math> … || Krümmung | ||
| + | |- | ||
| + | | <math> M </math> … || Moment | ||
| + | |- | ||
| + | | <math> d </math> … || statische Nutzhöhe | ||
| + | |- | ||
| + | | <math> \varepsilon_c </math> … || Betondehnung an der Bauteiloberkante | ||
| + | |- | ||
| + | | <math> \varepsilon_{s2} </math> … || Dehnung der Zugbewehrung im gerissenen Zustand im Riss (reiner Zustand II) | ||
| + | |- | ||
| + | | <math> \varepsilon_{sm} </math> … || mittlere Dehnung der Zugbewehrung | ||
| + | |- | ||
| + | | <math> EI^{II}_r </math> … || Biegesteifigkeit im reinen Zustand II | ||
| + | |- | ||
| + | | <math> EI^{II}_m </math> … || Biegesteifigkeit im Zustand II unter Berücksichtigung der Mitwirkung des Betons zwischen den Rissen | ||
| + | |}</li> | ||
| + | |||
| + | Im Zustand I spielt die Zugversteifung wegen der nicht vorhandenen Risse keine Rolle; mit zunehmender Rissbildung nimmt ihr Einfluss auf die Steifigkeit zu. | ||
| + | |||
| + | Die Berücksichtigung der Mitwirkung des Betons zwischen den Rissen ist bei allen Nachweisen die mit der Verformungen des Bauteils zusammenhängen und einer wirklichkeitsnahen Beschreibung des Bauteilverhaltens bedürfen empfehlenswert (z.B. Verformungsnachweis, Rotationsnachweis). Auch die Berechnung der Rissbreiten wird durch die Zugversteifung beeinflusst. | ||
| + | |||
| + | Abhängig vom Nachweis kann die Zugversteifung einen positiven oder negativen Einfluss auf das Nachweisergebnis haben <ref name="DAfStb600">Deutscher Aussschuss für Stahlbeton: Erläuterungen zu DIN EIN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode 2); DAfStb Heft 600</ref>. Beim Verformungsnachweis hat sie einen positiven Einfluss, da durch die höhere Steifigkeit die Verformungen abnehmen. Auf die Rotationsfähigkeit hat die Mitwirkung des Betons zwischen den Rissen einen negativen Einfluss, da durch die Zugversteifung die maximalen Stahldehnungen nicht in allen Bereichen voll aktiviert werden können. | ||
=Einflussfaktoren= | =Einflussfaktoren= | ||
| − | Die Mitwirkung des Betons zwischen den Rissen ist maßgeblich von den Verbundeigenschaften abhängig (z.B. Oberflächenbeschaffenheit der Stähle, Betonfestigkeit, Lage des Stabs im Bauteil, Stabdurchmesser). Je besser die Verbundbedingungen sind, desto größer ist die Mitwirkung des Betons zwischen den Rissen. | + | Die Mitwirkung des Betons zwischen den Rissen ist maßgeblich von den Verbundeigenschaften abhängig (z.B. Oberflächenbeschaffenheit der Stähle, Betonfestigkeit, Lage des Stabs im Bauteil, Stabdurchmesser). Je besser die Verbundbedingungen sind, desto größer ist auch die Mitwirkung des Betons zwischen den Rissen. |
| − | Außerdem | + | Außerdem wird die Zugversteifung durch den Rissabstand beeinflusst; je größer der Rissabstand ist, desto größer ist die Mitwirkung des Betons zwischen den Rissen. |
| − | Ein weitere Einflussfaktor ist die der Verlauf der Stahlkennlinie zwischen der Streckgrenze und der Zugfestigkeit bzw. der Abstand zwischen beiden Punkten. Ist der Abstand zwischen beiden Punkten gering bzw. der Verlauf flach, führt bereits eine kleine Abnahme der Spannungen zu einer großen Dehnungsabnahme. | + | Ein weitere Einflussfaktor ist die der Verlauf der Stahlkennlinie zwischen der Streckgrenze und der Zugfestigkeit bzw. der Abstand zwischen beiden Punkten. Ist der Abstand zwischen beiden Punkten gering bzw. der Verlauf flach, führt bereits eine kleine Abnahme der Spannungen zu einer großen Dehnungsabnahme <ref name="eligehausen98">Eligehausen, R. et al.: Mitwirkung des Betons zwischen den Rissen bei nichtelastischen Stahldehnungen - Optimierung des Verbunds; Beton- und Stahlbetonbau 93 (1998), Heft 2</ref>. |
| − | Einen großen Einfluss auf die Mitwirkung des Betons zwischen den Rissen hat außerdem der Bewehrungsgrad. Bei kleinen Bewehrungsgraden ist der Unterschied zwischen Stahldehnung im Riss und der mittleren Stahldehnung und somit die Mitwirkung des Betons bei sonst gleichbleiben Bedingungen größer als bei einem großen Bewehrungsgrad, da die Stahldehnungen bei der Rissbildung größer sind und eine größere Spannungsabnahme zwischen den Rissen stattfindet | + | Einen großen Einfluss auf die Mitwirkung des Betons zwischen den Rissen hat außerdem der Bewehrungsgrad. Bei kleinen Bewehrungsgraden ist der Unterschied zwischen Stahldehnung im Riss und der mittleren Stahldehnung und somit die Mitwirkung des Betons bei sonst gleichbleiben Bedingungen größer als bei einem großen Bewehrungsgrad, da die Stahldehnungen bei der Rissbildung größer sind und eine größere Spannungsabnahme zwischen den Rissen stattfindet<ref name="eligehausen98"></ref>. |
=Rechnerische Berücksichtigung der Zugversteifung= | =Rechnerische Berücksichtigung der Zugversteifung= | ||
| − | Für die rechnerische Berücksichtigung der Mitwirkung des Betons zwischen den Rissen wurden unterschiedliche Modelle entwickelt | + | Für die rechnerische Berücksichtigung der Mitwirkung des Betons zwischen den Rissen wurden unterschiedliche Modelle entwickelt. Sie kann entweder stahlseitig oder betonseitig berücksichtigt werden <ref name="quast10"></ref>. |
| − | + | Im Folgenden wird näher auf mögliche Verfahren eingegangen <ref name="quast10">Quast, U.: Zur Auswahl eines geeigneten Verfahrens für die Berücksichtigung der Mitwirkung des Betons auf Zug; Bautechnik 87 (2010), Heft 7</ref>, ausführlich vorgestellt wird aber nur die Modifizierung der Arbeitslinie des Stahls. Hierbei handelt es sich um das Modell, welches in den Erläuterungen zum EC2 (DAfStb Heft 600)<ref name="DAfStb600"></ref> vorgeschlagen wird. | |
| − | |||
| − | |||
| − | Im Folgenden wird | + | Die Auswahl des Verfahrens sollte abhängig von den Randbedingungen der Bemessungsaufgabe gewählt werden. Die Modifizierung der Arbeitslinie des Stahls, wie sie in DAfStb 600 )<ref name="DAfStb600"></ref> vorgestellt wird, ergbibt beispielsweise nur bei reiner Biegung befriedigende Ergebnisse <ref name="quast10"></ref>. |
| + | |||
| + | ==Betonseitige Berücksichtigung== | ||
| + | |||
| + | Grundlage aller betonseitigen Verfahren ist, dass dem Beton in der Zugzone auch nach der Rissbildung noch eine Zugspannung zugewiesen wird. In der Regel werden die Risse hierbei über die Bauteillänge verschmiert, sodass von einer konstanten Verteilung der Zugspannungen im Beton ausgegangen werden kann. Aus der so ermittelten Zugspannung im Beton wird anschließend die Betondehnung ermittelt, welche von der Stahldehnung im Riss abgezogen wird. Ergebnis ist eine über die Bauteillänge mittlere Stahldehnung. Durch die Annahme einer stetigen Wirkung der Zugversteifung ist das Ebenbleiben der Querschnitte weiterhin gegeben <ref name="quast10"></ref>. | ||
| + | |||
| + | <math>\varepsilon_{ct}=\frac{\sigma_{ct}}{E_{c,eff}}</math> | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{s2}-\varepsilon_{ct}</math> | ||
| + | |||
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | <math> \sigma_{ct} </math> … || Betonzugspannung | ||
| + | |- | ||
| + | | <math> \varepsilon_{ct} </math> … || Betondehnung | ||
| + | |- | ||
| + | | <math> E_{c,eff} </math> … || effektives Elastizitätsmodul des Betons | ||
| + | |- | ||
| + | | <math> \varepsilon_{s2} </math> … || Stahldehnung im gerissenen Zustand im Riss | ||
| + | |- | ||
| + | | <math> \varepsilon_{sm} </math> … || mittlere Stahldehnung | ||
| + | |}</li> | ||
| + | |||
| + | Die Höhe der dem Beton zugewiesenen Spannungen werden in unterschiedlichen Verfahren unterschiedlich angenommen. Im Folgenden werden gängige Annahmen betrachtet <ref name="quast10"></ref>. | ||
| + | |||
| + | ===Abnehmende Betonzugspannung=== | ||
| + | |||
| + | [[File:Mitwirkung_des_Betons_zwischen_den_Rissen_(Zugversteifung)_3.jpg|right|thumb|350px|Zugbereich des Betongesetzes <ref name="kretz09"></ref> ]] | ||
| + | |||
| + | Es werden Betonzugspannungen f<sub>ct</sub> angesetzt, die bei Erreichen einer Grenzdehnung ε<sub>ctu</sub> auf Null abfallen. Die Größe der Grenzdehnung wird in der Literatur unterschiedlich abgegeben, wobei sie ca. dem 8- bis 10-fachen der Betondehnung bei Erreichen der Zugfestigkeit entspricht ε<sub>ct</sub> <ref name="kretz09">Kretz, J.: Grundlagen zu Verformungsberechnungen für überwiegend auf Biegung beanspruchte Stahlbetonquerschnitte unter Berücksichtigung des Reißens des Betons; mb-news (2009); Nr.4; 38-46</ref>. Zwischen dem Erreichen der Dehnung bei Erreichen der Betonzugfestigkeit ε<sub>ct</sub> und der Grenzdehnung ε<sub>ctu</sub> fallen die Zugspannungen ab, der Verlauf der Zugspannungen in diesem Bereich ist abhängig vom Bewehrungsgrad <ref name="kretz09"></ref>. Bei geringen Bewehrungsgraden ist der Verlauf nahezu linear, bei hohen nimmt die Betonzugspannung zunächst stärker ab und verläuft danach flach weiter bis zur Erreichung der Grenzdehnung ε<sub>ctu</sub> <ref name="kretz09"></ref>. | ||
| + | |||
| + | ===konstante Betonzugspannung im Wirkungsbereich der Zugbewehrung=== | ||
| + | |||
| + | Die Betonzugspannung wird im Wirkungsbereich der Bewehrung als konstant angenommen. Als Wirkungsbereich der Zugbewehrung wird beginnent am Zugrand der 2,5 Abstand zwischen Schwereachse der Bewehrung und dem Zugrand angenommen (<math>2,5\cdot d_1</math>). Als konstante Zugspannung wird die Hälfte der Zugfestigkeit angesetzt <ref name="quast10"></ref>. | ||
| + | |||
| + | <math>\sigma_{ct}=\frac{f_{ct}}{2}</math> | ||
| + | |||
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | <math> f_{ct} </math> … || Betonzugfestigkeit | ||
| + | |}</li> | ||
| + | |||
| + | ==Modifizierung der Arbeitslinie des Stahls== | ||
| + | |||
| + | Auch bei diesem Verfahren ist das Ergebnis einer über die Bauteillänge konstante mittlere Stahldehnung, sodass die Hypothese von Bernoulli weiterhin gilt. | ||
| + | |||
| + | [[File:Mitwirkung_des_Betons_zwischen_den_Rissen_(Zugversteifung)_2.jpg|right|thumb|350px|Modifizierte Spannungs-Dehnungs-Linie für Betonstahl zur Berücksichtigung der Mitwirkung des Betons zwischen den Rissen (nach <ref name="DAfStb600"></ref>) ]] | ||
| + | |||
| + | Für die Modifizierung der Arbeitslinie des Stahls stehen abhängig vom Bereich der Arbeitslinie unterschiedliche Formeln zur Verfügung. Die folgenden Gleichungen gelten für linearisierte Spannungs-Dehnungs-Linien mit den üblichen vier Abschnitten<ref name="DAfStb600"></ref>. | ||
| + | |||
| + | '''ungerissener Bereich:''' <math>0<\sigma_s\leq \sigma_{s,cr}</math> | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{s1}</math> | ||
| + | |||
| + | '''Zustand der Erstrissbildung:''' <math>\sigma_{s,cr}<\sigma_s\leq1,3\cdot\sigma_{s,cr}</math> | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{s2}-\frac{\beta_t\cdot\left(\sigma_s-\sigma_{s,cr}\right)+\left(1,3\cdot\sigma_{s,cr}-\sigma_s\right)}{0,3\cdot\sigma_{s,cr}}\cdot\left(\varepsilon_{s,cr2}-\varepsilon_{s,cr1}\right)</math> | ||
| + | |||
| + | |||
| + | '''abgeschlossene Rissbildung:''' <math>1,3\cdot\sigma_{s,cr}<\sigma_s\leq f_y</math> | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{s2}-\beta_t\cdot\left(\varepsilon_{s,cr2}-\varepsilon_{s,cr1}\right)</math> | ||
| + | |||
| + | |||
| + | '''Fließen des Betonstahls:''' <math>f_y<\sigma_s\leq f_t</math> | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{sy}-\beta_t\cdot\left(\varepsilon_{s,cr2}-\varepsilon_{s,cr1}\right)+\delta_t\cdot\left(1-\frac{\sigma_{sr}}{f_y}\right)\cdot\left(\varepsilon_{s2}-\varepsilon_{sy}\right)</math> | ||
| + | |||
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | <math> \sigma_s </math> … || vorhandene Stahldehnung | ||
| + | |- | ||
| + | | <math> \sigma_{s,cr} </math> … || Stahldehnung die zur Erstrissbildung führt | ||
| + | |- | ||
| + | | <math> f_y </math> … || Festigkeit an der Streckgrenze | ||
| + | |- | ||
| + | | <math> f_t </math> … || Zugfestigkeit | ||
| + | |- | ||
| + | | <math> \varepsilon_{s1} </math> … || Stahldehnung im ungerissenen Zustand | ||
| + | |- | ||
| + | | <math> \varepsilon_{s2} </math> … || Stahldehnung im gerissenen Zustand im Riss | ||
| + | |- | ||
| + | | <math> \varepsilon_{s,cr1} </math> … || Stahldehnung im ungerissenen Zustand unter Rissschnittgrößen bei Erreichen von f<sub>ctm</sub> | ||
| + | |- | ||
| + | | <math> \varepsilon_{s,cr2} </math> … || Stahldehnung im Riss unter Rissschnittgrößen | ||
| + | |- | ||
| + | | <math> \varepsilon_{y} </math> … || Dehnung im gerissenen Zustand an der Streckgrenze | ||
| + | |- | ||
| + | | <math> \beta_t </math> … || Beiwert zur Berücksichtigung des Einflüsses der Belastungsdauer oder einer wiederholten Belastung auf die mittlere Dehnung (=0,40 für eine einzelne kurzzeitige Belastung; =0,25 für eine andauernde Last oder für häufige Lastwechsel) | ||
| + | |- | ||
| + | | <math> \delta_d </math> … || Beiwert zur Berücksichtigung der Duktilität der Bewehrung (=0,80 für hochduktilen Stahl B500B; =0,6 für normalduktilen Stahl B500A) | ||
| + | |}</li> | ||
| + | |||
| + | <math>\varepsilon_{c1,cr1}=\frac{f_{ctm}}{E_{cm}}</math> | ||
| + | |||
| + | <math>\varepsilon_{c2,cr1}=-\varepsilon_{c1,cr1}\cdot\frac{z_{I,c2}}{z_{I,c1}}</math> | ||
| + | |||
| + | <math>\varepsilon_{s,cr1}=\varepsilon_{c1,cr1}\cdot\frac{d-z_{I,c2}}{z_{I,c1}}</math> | ||
| + | |||
| + | <math>x=\frac{\alpha_e\cdot A_{s1}}{b}\cdot\left(-1+\sqrt{1+\frac{2\cdot b\cdot d}{\alpha_e\cdot A_{s1}}}\right)</math> | ||
| + | |||
| + | <math>z=d-\frac{x}{3}</math> | ||
| + | |||
| + | <math>\sigma_{s,cr2}=\frac{M_{cr}}{z\cdot A_{s1}}</math> | ||
| + | |||
| + | <math>\varepsilon_{s,cr2}=\frac{\sigma_{s,cr2}}{E_s}</math> | ||
| + | |||
| + | Vereinfachend kann der Rissbildungsprozess auch unberücksichtigt bleiben<ref name="DAfStb600"></ref>. Hierdurch entfällt die zweite der zuvor aufgeführten Gleichungen, die restlichen Gleichungen bleiben unverändert, die Grenzen der verbliebenen Bereiche werden im Folgende dargestellt: | ||
| + | |||
| + | '''ungerissener Bereich:''' <math>0<\sigma_s\leq \beta_t\cdot\sigma_{s,cr}</math> | ||
| + | |||
| + | '''abgeschlossene Rissbildung:''' <math>\beta_t\cdot\sigma_{s,cr}<\sigma_s\leq f_y</math> | ||
| + | |||
| + | '''Fließen des Betonstahls:''' <math>f_y<\sigma_s\leq f_t</math> | ||
| + | |||
| + | Die Verwendung der vereinfachten Gleichungen ist empfehlenswert, wenn von wiederholter Be- und Entlastung ausgegangen wird, da der Rissbildungsprozess nur bei der ersten Belastung über dem Rissbildungsmoment stattfindet <ref name=podeyn14>Podeyn, D.: Überlegungen zur Verformungsvorhersage von Spannbetonbrücken mit gerissener Zugzone; Dissertation (2014), Universität Rostock</ref>. | ||
| + | |||
| + | [[Mitwirkung des Betons zwischen den Rissen (Bsp.)|Beispiel zur Ermittlung der MItwirkung des Betons zwischen den Rissen]] | ||
| + | |||
| + | =Quellen= | ||
| + | <references /> | ||
| + | <br /> | ||
| − | + | {{Seiteninfo | |
| + | |Quality-flag = [[File:quality-flag-white.gif|right|70px]] | ||
| + | |Status = Seite in Bearbeitung}} | ||
| − | + | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | |
Aktuelle Version vom 10. August 2024, 21:42 Uhr
Als Mitwirkung des Betons zwischen den Rissen (auch Zugversteifung bzw. engl. "tension stiffening") wird der Effekt bezeichnet, dass die Stahlspannungen und somit auch die Stahlspannungen zwischen den Rissen abnehmen. Die Mitwirkung des Betons zwischen den Rissen beeinflusst maßgeblich die Steifigkeit des Bauteils im Zustand II.
Allgemeines
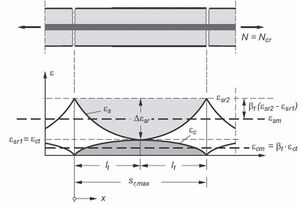
Grund für die Abnahme der Stahldehnungen zwischen den Rissen ist der Verbund zwischen Stahl und Beton. Im Riss ist kein Verbund zwischen Stahl und Beton mehr vorhanden, die Stahlspannung ist hier maximal. Zwischen den Rissen findet durch den Verbund von Stahl und Beton eine Kraftübertragung zwischen beiden Materialien statt; der Beton nimmt zwischen den Rissen ebenfalls Zugspannungen auf, sodass die Stahlspannung und -dehnung hier abnehmen. Mittig zwischen den Rissen wird die Stahlspannung minimal.
Durch die Abnahme der Dehnungen zwischen den Rissen nimmt die Bauteilsteifigkeit im Vergleich zum reinen Zustand II zu. Dieser Effekt lässt sich anschaulich an den Krümmungen veranschaulichen, welche gemäß den Grundsätzen der Mechanik mit der Steifigkeit direkt zusammenhängen. Im Folgenden wird dies am Beispiel des Biegebalkens dargestellt.
Betrachtet man die folgenden Gleichungen und setzt voraus, dass Moment und statische Nutzhöhe gleichbleiben, führt die Verringerung der Stahldehnung zu einer Vergrößerung der Biegesteifigkeit.
wenn gilt dann gilt ebenfalls
wobei:
… Krümmung … Moment … statische Nutzhöhe … Betondehnung an der Bauteiloberkante … Dehnung der Zugbewehrung im gerissenen Zustand im Riss (reiner Zustand II) … mittlere Dehnung der Zugbewehrung … Biegesteifigkeit im reinen Zustand II … Biegesteifigkeit im Zustand II unter Berücksichtigung der Mitwirkung des Betons zwischen den Rissen
Im Zustand I spielt die Zugversteifung wegen der nicht vorhandenen Risse keine Rolle; mit zunehmender Rissbildung nimmt ihr Einfluss auf die Steifigkeit zu.
Die Berücksichtigung der Mitwirkung des Betons zwischen den Rissen ist bei allen Nachweisen die mit der Verformungen des Bauteils zusammenhängen und einer wirklichkeitsnahen Beschreibung des Bauteilverhaltens bedürfen empfehlenswert (z.B. Verformungsnachweis, Rotationsnachweis). Auch die Berechnung der Rissbreiten wird durch die Zugversteifung beeinflusst.
Abhängig vom Nachweis kann die Zugversteifung einen positiven oder negativen Einfluss auf das Nachweisergebnis haben [2]. Beim Verformungsnachweis hat sie einen positiven Einfluss, da durch die höhere Steifigkeit die Verformungen abnehmen. Auf die Rotationsfähigkeit hat die Mitwirkung des Betons zwischen den Rissen einen negativen Einfluss, da durch die Zugversteifung die maximalen Stahldehnungen nicht in allen Bereichen voll aktiviert werden können.
Einflussfaktoren
Die Mitwirkung des Betons zwischen den Rissen ist maßgeblich von den Verbundeigenschaften abhängig (z.B. Oberflächenbeschaffenheit der Stähle, Betonfestigkeit, Lage des Stabs im Bauteil, Stabdurchmesser). Je besser die Verbundbedingungen sind, desto größer ist auch die Mitwirkung des Betons zwischen den Rissen.
Außerdem wird die Zugversteifung durch den Rissabstand beeinflusst; je größer der Rissabstand ist, desto größer ist die Mitwirkung des Betons zwischen den Rissen.
Ein weitere Einflussfaktor ist die der Verlauf der Stahlkennlinie zwischen der Streckgrenze und der Zugfestigkeit bzw. der Abstand zwischen beiden Punkten. Ist der Abstand zwischen beiden Punkten gering bzw. der Verlauf flach, führt bereits eine kleine Abnahme der Spannungen zu einer großen Dehnungsabnahme [3].
Einen großen Einfluss auf die Mitwirkung des Betons zwischen den Rissen hat außerdem der Bewehrungsgrad. Bei kleinen Bewehrungsgraden ist der Unterschied zwischen Stahldehnung im Riss und der mittleren Stahldehnung und somit die Mitwirkung des Betons bei sonst gleichbleiben Bedingungen größer als bei einem großen Bewehrungsgrad, da die Stahldehnungen bei der Rissbildung größer sind und eine größere Spannungsabnahme zwischen den Rissen stattfindet[3].
Rechnerische Berücksichtigung der Zugversteifung
Für die rechnerische Berücksichtigung der Mitwirkung des Betons zwischen den Rissen wurden unterschiedliche Modelle entwickelt. Sie kann entweder stahlseitig oder betonseitig berücksichtigt werden [4].
Im Folgenden wird näher auf mögliche Verfahren eingegangen [4], ausführlich vorgestellt wird aber nur die Modifizierung der Arbeitslinie des Stahls. Hierbei handelt es sich um das Modell, welches in den Erläuterungen zum EC2 (DAfStb Heft 600)[2] vorgeschlagen wird.
Die Auswahl des Verfahrens sollte abhängig von den Randbedingungen der Bemessungsaufgabe gewählt werden. Die Modifizierung der Arbeitslinie des Stahls, wie sie in DAfStb 600 )[2] vorgestellt wird, ergbibt beispielsweise nur bei reiner Biegung befriedigende Ergebnisse [4].
Betonseitige Berücksichtigung
Grundlage aller betonseitigen Verfahren ist, dass dem Beton in der Zugzone auch nach der Rissbildung noch eine Zugspannung zugewiesen wird. In der Regel werden die Risse hierbei über die Bauteillänge verschmiert, sodass von einer konstanten Verteilung der Zugspannungen im Beton ausgegangen werden kann. Aus der so ermittelten Zugspannung im Beton wird anschließend die Betondehnung ermittelt, welche von der Stahldehnung im Riss abgezogen wird. Ergebnis ist eine über die Bauteillänge mittlere Stahldehnung. Durch die Annahme einer stetigen Wirkung der Zugversteifung ist das Ebenbleiben der Querschnitte weiterhin gegeben [4].
wobei:
… Betonzugspannung … Betondehnung … effektives Elastizitätsmodul des Betons … Stahldehnung im gerissenen Zustand im Riss … mittlere Stahldehnung
Die Höhe der dem Beton zugewiesenen Spannungen werden in unterschiedlichen Verfahren unterschiedlich angenommen. Im Folgenden werden gängige Annahmen betrachtet [4].
Abnehmende Betonzugspannung
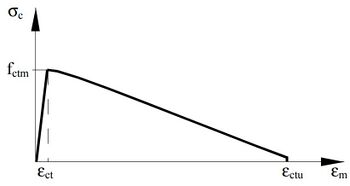
Es werden Betonzugspannungen fct angesetzt, die bei Erreichen einer Grenzdehnung εctu auf Null abfallen. Die Größe der Grenzdehnung wird in der Literatur unterschiedlich abgegeben, wobei sie ca. dem 8- bis 10-fachen der Betondehnung bei Erreichen der Zugfestigkeit entspricht εct [5]. Zwischen dem Erreichen der Dehnung bei Erreichen der Betonzugfestigkeit εct und der Grenzdehnung εctu fallen die Zugspannungen ab, der Verlauf der Zugspannungen in diesem Bereich ist abhängig vom Bewehrungsgrad [5]. Bei geringen Bewehrungsgraden ist der Verlauf nahezu linear, bei hohen nimmt die Betonzugspannung zunächst stärker ab und verläuft danach flach weiter bis zur Erreichung der Grenzdehnung εctu [5].
konstante Betonzugspannung im Wirkungsbereich der Zugbewehrung
Die Betonzugspannung wird im Wirkungsbereich der Bewehrung als konstant angenommen. Als Wirkungsbereich der Zugbewehrung wird beginnent am Zugrand der 2,5 Abstand zwischen Schwereachse der Bewehrung und dem Zugrand angenommen (). Als konstante Zugspannung wird die Hälfte der Zugfestigkeit angesetzt [4].
wobei:
… Betonzugfestigkeit
Modifizierung der Arbeitslinie des Stahls
Auch bei diesem Verfahren ist das Ergebnis einer über die Bauteillänge konstante mittlere Stahldehnung, sodass die Hypothese von Bernoulli weiterhin gilt.

Für die Modifizierung der Arbeitslinie des Stahls stehen abhängig vom Bereich der Arbeitslinie unterschiedliche Formeln zur Verfügung. Die folgenden Gleichungen gelten für linearisierte Spannungs-Dehnungs-Linien mit den üblichen vier Abschnitten[2].
ungerissener Bereich:
Zustand der Erstrissbildung:
abgeschlossene Rissbildung:
Fließen des Betonstahls:
wobei:
… vorhandene Stahldehnung … Stahldehnung die zur Erstrissbildung führt … Festigkeit an der Streckgrenze … Zugfestigkeit … Stahldehnung im ungerissenen Zustand … Stahldehnung im gerissenen Zustand im Riss … Stahldehnung im ungerissenen Zustand unter Rissschnittgrößen bei Erreichen von fctm … Stahldehnung im Riss unter Rissschnittgrößen … Dehnung im gerissenen Zustand an der Streckgrenze … Beiwert zur Berücksichtigung des Einflüsses der Belastungsdauer oder einer wiederholten Belastung auf die mittlere Dehnung (=0,40 für eine einzelne kurzzeitige Belastung; =0,25 für eine andauernde Last oder für häufige Lastwechsel) … Beiwert zur Berücksichtigung der Duktilität der Bewehrung (=0,80 für hochduktilen Stahl B500B; =0,6 für normalduktilen Stahl B500A)
Vereinfachend kann der Rissbildungsprozess auch unberücksichtigt bleiben[2]. Hierdurch entfällt die zweite der zuvor aufgeführten Gleichungen, die restlichen Gleichungen bleiben unverändert, die Grenzen der verbliebenen Bereiche werden im Folgende dargestellt:
ungerissener Bereich:
abgeschlossene Rissbildung:
Fließen des Betonstahls:
Die Verwendung der vereinfachten Gleichungen ist empfehlenswert, wenn von wiederholter Be- und Entlastung ausgegangen wird, da der Rissbildungsprozess nur bei der ersten Belastung über dem Rissbildungsmoment stattfindet [6].
Beispiel zur Ermittlung der MItwirkung des Betons zwischen den Rissen
Quellen
- ↑ Zilch,K., Zehetmaier,G.: Bemessung im konstruktiven Betonbau; 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Deutscher Aussschuss für Stahlbeton: Erläuterungen zu DIN EIN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode 2); DAfStb Heft 600
- ↑ 3,0 3,1 Eligehausen, R. et al.: Mitwirkung des Betons zwischen den Rissen bei nichtelastischen Stahldehnungen - Optimierung des Verbunds; Beton- und Stahlbetonbau 93 (1998), Heft 2
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 Quast, U.: Zur Auswahl eines geeigneten Verfahrens für die Berücksichtigung der Mitwirkung des Betons auf Zug; Bautechnik 87 (2010), Heft 7
- ↑ 5,0 5,1 5,2 5,3 Kretz, J.: Grundlagen zu Verformungsberechnungen für überwiegend auf Biegung beanspruchte Stahlbetonquerschnitte unter Berücksichtigung des Reißens des Betons; mb-news (2009); Nr.4; 38-46
- ↑ Podeyn, D.: Überlegungen zur Verformungsvorhersage von Spannbetonbrücken mit gerissener Zugzone; Dissertation (2014), Universität Rostock
Seiteninfo
|
















































