Mitwirkung des Betons zwischen den Rissen (Bsp.): Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Auf dieser Seite wird beispielhaft die Mitwirkung des Betons zwischen den Rissen ermittelt, die Theorie hierfür wird auf einer gesonderten Seite dargestellt (…“) |
EWill (Diskussion | Beiträge) K |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
* Kurzzeitbelastung | * Kurzzeitbelastung | ||
| − | =Festigkeiten= | + | =Modifizierung der Arbeitslinie des Stahls= |
| + | |||
| + | ==Festigkeiten== | ||
<math>f_{yR}=1,1\cdot500=550\frac{N}{mm^2}=55\frac{kN}{cm^2}</math> | <math>f_{yR}=1,1\cdot500=550\frac{N}{mm^2}=55\frac{kN}{cm^2}</math> | ||
| Zeile 20: | Zeile 22: | ||
<math>f_{ctm}=2,2\frac{N}{mm^2}=0,22\frac{kN}{cm^2}</math> | <math>f_{ctm}=2,2\frac{N}{mm^2}=0,22\frac{kN}{cm^2}</math> | ||
| − | =Vorbereitende Berechnung= | + | ==Vorbereitende Berechnung== |
| − | ==Ermittlung des Rissbildungsmoments== | + | ===Ermittlung des Rissbildungsmoments=== |
<math>I_I=\frac{b\cdot h^3}{12}=\frac{100\cdot25^3}{12}=130208cm^4</math> | <math>I_I=\frac{b\cdot h^3}{12}=\frac{100\cdot25^3}{12}=130208cm^4</math> | ||
| Zeile 30: | Zeile 32: | ||
<math>M_{cr}=\frac{0,22\cdot130208}{12,5}=2292kNcm</math> | <math>M_{cr}=\frac{0,22\cdot130208}{12,5}=2292kNcm</math> | ||
| − | ==Ermittlung der Stahldehnung im Riss unter den Rissschnittgrößen== | + | ===Ermittlung der Stahldehnung im Riss unter den Rissschnittgrößen=== |
<math>\alpha_e=\frac{200000}{10000}=20</math> | <math>\alpha_e=\frac{200000}{10000}=20</math> | ||
| Zeile 44: | Zeile 46: | ||
<math>\varepsilon_{s,cr2}=\frac{20,92}{20000}=1,041\dot10^{-3}</math> | <math>\varepsilon_{s,cr2}=\frac{20,92}{20000}=1,041\dot10^{-3}</math> | ||
| − | =Ermittlung der mittleren Stahldehnungen im ungerissenen Zustand= | + | ==Ermittlung der mittleren Stahldehnungen im ungerissenen Zustand== |
<math>\varepsilon_{c1,cr1}=\varepsilon_{c2,cr1}=\frac{f_{ctm}}{E_{cm}}=\frac{0,22}{1000}=0,22\cdot10^{-3}</math> | <math>\varepsilon_{c1,cr1}=\varepsilon_{c2,cr1}=\frac{f_{ctm}}{E_{cm}}=\frac{0,22}{1000}=0,22\cdot10^{-3}</math> | ||
| Zeile 54: | Zeile 56: | ||
Da im Zustand I noch keine Risse vorhanden sind, entspricht die mittlere Stahldehnung der Stahldehnung. | Da im Zustand I noch keine Risse vorhanden sind, entspricht die mittlere Stahldehnung der Stahldehnung. | ||
| − | =Ermittlung der mittleren Stahldehnung bei Erreichen der Streckgrenze= | + | ==Ermittlung der mittleren Stahldehnung bei Erreichen der Streckgrenze== |
Dehnung an der Streckgrenze: <math>\varepsilon_{s2}=\varepsilon_{sy}=\frac{55}{20000}=2,75\cdot 10^{-3}</math> | Dehnung an der Streckgrenze: <math>\varepsilon_{s2}=\varepsilon_{sy}=\frac{55}{20000}=2,75\cdot 10^{-3}</math> | ||
| Zeile 66: | Zeile 68: | ||
<math>\underline{\underline{\varepsilon_{smy}=2,4076\cdot 10^{-3}}}</math> | <math>\underline{\underline{\varepsilon_{smy}=2,4076\cdot 10^{-3}}}</math> | ||
| − | =Ermittlung der mittleren Stahldehnung zum Zeitpunkt des Bruchs= | + | ==Ermittlung der mittleren Stahldehnung zum Zeitpunkt des Bruchs== |
Die Stahldehnung im Riss unter den Rissschnittgrößen wurde mithilfe der gegebenen Querschnittsgeometrie und Bewehrung mithilfe der ω-Tafeln ermittelt. Für die Ermittlung wurde die rechnerische Zugfestigkeit verwendet. | Die Stahldehnung im Riss unter den Rissschnittgrößen wurde mithilfe der gegebenen Querschnittsgeometrie und Bewehrung mithilfe der ω-Tafeln ermittelt. Für die Ermittlung wurde die rechnerische Zugfestigkeit verwendet. | ||
| Zeile 78: | Zeile 80: | ||
<math>\underline{\underline{\varepsilon_{smt}=12,46\cdot 10^{-3}}}</math> | <math>\underline{\underline{\varepsilon_{smt}=12,46\cdot 10^{-3}}}</math> | ||
| − | =Einfluss des Bewehrungsgrads auf die Mitwirkung des Betons zwischen den Rissen= | + | ==Einfluss des Bewehrungsgrads auf die Mitwirkung des Betons zwischen den Rissen== |
Im Folgenden soll der Einfluss des Bewehrungsgrads auf die Mitwirkung des Betons zwischen den Rissen an diesem Beispiel verdeutlich werden. | Im Folgenden soll der Einfluss des Bewehrungsgrads auf die Mitwirkung des Betons zwischen den Rissen an diesem Beispiel verdeutlich werden. | ||
| Zeile 88: | Zeile 90: | ||
Aus dem Diagramm geht hervor, dass der Einfluss der Mitwirkung des Betons zwischen den Rissen mit steigendem Bewehrungsgrad abnimmt. Außerdem ist zu erkennen, dass Einfluss ab einem gewissen Bewehrungsgrad weniger stark abnimmt bzw. nahezu gleichbleibet. | Aus dem Diagramm geht hervor, dass der Einfluss der Mitwirkung des Betons zwischen den Rissen mit steigendem Bewehrungsgrad abnimmt. Außerdem ist zu erkennen, dass Einfluss ab einem gewissen Bewehrungsgrad weniger stark abnimmt bzw. nahezu gleichbleibet. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Seiteninfo | {{Seiteninfo | ||
Aktuelle Version vom 12. August 2024, 21:48 Uhr
Auf dieser Seite wird beispielhaft die Mitwirkung des Betons zwischen den Rissen ermittelt, die Theorie hierfür wird auf einer gesonderten Seite dargestellt (vgl. Mitwirkung des Betons zwischen den Rissen.
Aufgabenstellung
Für eine Platte mit Rechteckquerschnitt und gegebener Bewehrung sollen die Mitwirkung des Betons im ungerissenen Zustand, bei Erreichung der Streckgrenze und zum Zeitpunkt des Bruchs berechnet werden. Als Festigkeiten sind die rechnerischen Mittelwerte anzusetzen
- b/h=100cm/25cm
- d=23cm
- B500A
- Längsbewehrung: R524 (As,vorh=5,24cm²)
- C 20/25
- (Mit der Berücksichtigung von Kriecheinflüssen)
- Kurzzeitbelastung
Modifizierung der Arbeitslinie des Stahls
Festigkeiten
Vorbereitende Berechnung
Ermittlung des Rissbildungsmoments
Ermittlung der Stahldehnung im Riss unter den Rissschnittgrößen
Ermittlung der mittleren Stahldehnungen im ungerissenen Zustand
Da im Zustand I noch keine Risse vorhanden sind, entspricht die mittlere Stahldehnung der Stahldehnung.
Ermittlung der mittleren Stahldehnung bei Erreichen der Streckgrenze
Dehnung an der Streckgrenze:
(Kurzzeitbelastung)
Ermittlung der mittleren Stahldehnung zum Zeitpunkt des Bruchs
Die Stahldehnung im Riss unter den Rissschnittgrößen wurde mithilfe der gegebenen Querschnittsgeometrie und Bewehrung mithilfe der ω-Tafeln ermittelt. Für die Ermittlung wurde die rechnerische Zugfestigkeit verwendet.
Einfluss des Bewehrungsgrads auf die Mitwirkung des Betons zwischen den Rissen
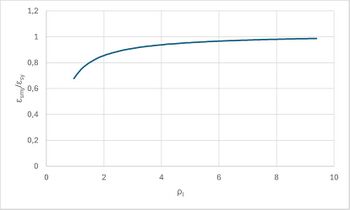
Im Folgenden soll der Einfluss des Bewehrungsgrads auf die Mitwirkung des Betons zwischen den Rissen an diesem Beispiel verdeutlich werden. Hierfür wird das Verhältnis der mittleren Stahldehnung zur Stahldehnung im Riss für unterschiedliche Bewehrungsgrade mit den hier vorgestellten Gleichungen ermittelt. Betrachtet werden die Dehnungen bei Erreichen der Streckgrenze.
Der Bewehrungsgrad wird zwischen dem minimal für die Sicherstellung der Duktilität erforderlichen und dem maximal ohne Druckbewehrung möglichen variiert.
Aus dem Diagramm geht hervor, dass der Einfluss der Mitwirkung des Betons zwischen den Rissen mit steigendem Bewehrungsgrad abnimmt. Außerdem ist zu erkennen, dass Einfluss ab einem gewissen Bewehrungsgrad weniger stark abnimmt bzw. nahezu gleichbleibet.
Seiteninfo
|