Verformungsnachweis - indirekte Berechnung: Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) K |
EWill (Diskussion | Beiträge) K |
||
| Zeile 41: | Zeile 41: | ||
| <math> \rho'=\frac{A_{s2,erf}}{b\cdot d} </math> … || erforderlicher Druckbewehrungsgrad in Feldmitte (bei Kragträgern an der Einspannstelle) | | <math> \rho'=\frac{A_{s2,erf}}{b\cdot d} </math> … || erforderlicher Druckbewehrungsgrad in Feldmitte (bei Kragträgern an der Einspannstelle) | ||
|- | |- | ||
| − | | <math> \rho_0=f_{ck}\cdot 10^{-3} </math> … || Referenzbewehrungsgrad | + | | <math> \rho_0=\sqrt{f_{ck}}\cdot 10^{-3} </math> … || Referenzbewehrungsgrad |
|- | |- | ||
| <math> l </math> … || [[Effektive Stützweite|effektive Stützweite]] | | <math> l </math> … || [[Effektive Stützweite|effektive Stützweite]] | ||
Version vom 26. August 2024, 20:26 Uhr
Im Rahmen der Nachweise im Grenzzustand der Gebrauchstauglichkeit ist auch ein Verformungsnachweis zu führen. Dieser kann indirekt über die Biegeschlankheit geführt werden oder über eine direkte Verformungsberechnung. Die indirekte Verformungsberechnung ist die einfachere der beiden Methoden, ist allerdings auch ungenauer.
Allgemeines
Der Verformungsnachweis kann immer dann über die Biegeschlankheit geführt werden, wenn keine erhöhten Anforderungen an die Durchbiegungsbegrenzung gestellt werden und folgende Voraussetzungen erfüllt sind[1]:
- Es handelt sich um einen Stahlbetonbalken bzw. eine Stahlbetonplatte des „üblichen“ Hochbaus.
- Das Bauteil wird nur durch Gleichlasten belastet.
- Das Bauteil unterliegt nur statische Beanspruchungen.
Das Verfahren darf nicht für Spannbetonbauteile und Bauteile, bei denen große Normalkräfte angreifen verwendet werden[1].
Der Verformungsnachweis über eine indirekte Verformungsberechnung kann mit zwei unterschiedlichen Varianten erfolgen. Beide werden im Folgenden näher vorgestellt.
Verfahren nach EC 2
In diesem Verfahren werden die wesentlichen Einflussfaktoren auf die Verformung näherungsweise erfasst. Die Einflussfaktoren auf die Verformungen, die berücksichtigt werden, sind Folgende[2]:
- Spannweite des Bauteils
- statisches System
- Trägheitsmoment (über die statische Nutzhöhe)
- Elastizitätsmodul des Betons (über die Betondruckfestigkeit)
- Ausdehnung des gerissenen Bereichs
- Bewehrungsgrad
Die letzten beiden Faktoren gehen durch die Unterscheidung in gering- und hochbeanspruchte Bauteile in die Berechnung ein. Die Unterscheidung findet über den Längsbewehrungsgrad statt. Liegt der Längsbewehrungsgrad über dem von der Betondruckfestigkeit abhängigen Referenzbewehrungsgrad, handelt es sich um ein hochbeanspruchtes Bauteil; liegt er darunter, ist das Bauteil als gering bzw. mäßig beansprucht einzustufen. Für beide Varianten steht jeweils eine separate Gleichung zur Verfügung[3]:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{wenn }\rho\leq\rho_0\qquad\qquad\frac{l}{d}\leq K\cdot\left[11+1,5\cdot\sqrt{f_{ck}}\cdot\frac{\rho_0}{\rho}+3,2\cdot\sqrt{f_{ck}}\cdot\left(\frac{\rho_0}{\rho}-1\right)^{\frac{3}{2}}\right]\leq\left(\frac{l}{d}\right)_{max}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{wenn }\rho>\rho_0\qquad\qquad\frac{l}{d}\leq K\cdot\left[11+1,5\cdot\sqrt{f_{ck}}\cdot\frac{\rho_0}{\rho-\rho'}+\frac{1}{12}\cdot\sqrt{f_{ck}}\cdot\left(\frac{\rho'}{\rho_0}\right)^{\frac{1}{2}}\right]\leq\left(\frac{l}{d}\right)_{max}}
wobei:
… erforderlicher ZUgbewehrungsgrad in Feldmitte (bei Kragträgern an der Einspannstelle) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho'=\frac{A_{s2,erf}}{b\cdot d} } … erforderlicher Druckbewehrungsgrad in Feldmitte (bei Kragträgern an der Einspannstelle) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_0=\sqrt{f_{ck}}\cdot 10^{-3} } … Referenzbewehrungsgrad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l } … effektive Stützweite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d } … statische Nutzhöhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K } … Beiwert zur Berücksichtigung des statischen Systems Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ck} } … charakteristische Druckfestigkeit des Betons Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{N}{mm^2}}
Da der Längsbewehrungsgrad in den Gleichungen den Einfluss der Beanspruchung wiederspiegeln soll, ist mit dem erforderlichen und nicht mit dem vorhandenen Bewehrungsgrad zu rechnen. Würde mit dem vorhandenen gerechnet werden, würden ungünstigere Ergebnisse erzielt werden, da die Beanspruchung überschätzt würde.
Die Gleichungen können bzw. müssen im Folgenden mit weiteren Faktoren modifiziert werden. Diese Faktoren resultieren aus Abweichungen zwischen den Eigenschaften des betrachteten Bauteils und den Eigenschaften der Bauteile, welche für die Kalibrierung der Gleichungen verwendet wurden[3].
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_1=\frac{310\frac{N}{mm^2}}{\sigma_{s1} [\frac{N}{mm^2}]}\qquad} wenn die vorhandene Stahlspannung unter der BemessungslastFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \neq310\frac{N}{mm^2}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_2=0,8\qquad} bei gegliederten Querschnitten (z.B. Plattenbalken, I-Profile) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_3=\frac{7,0}{l_{eff}[m]}\qquad} bei Balken und Platten mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l\geq7m} und erhöhten Anforderungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_3=\frac{8,5}{l_{eff}[m]}\qquad} bei Flachdecken mit und erhöhten Anforderungen
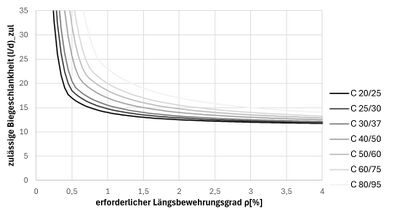
Aus der grafischen Auswertung der Gleichung ist deutlich erkennbar, dass die zulässige Biegeschlankheit mit steigendem Längsbewehrungsgrad und somit mit sinkender Beanspruchung zunimmt. Außerdem ist zu sehen, dass durch die zunehmende Biegesteifigkeit infolge zunehmender Betondruckfestigkeit, die zulässige Biegeschlankheit zunimmt. Beides stimmt mit den allgemeinen Zusammenhängen bezüglich der Bauteilverformungen überein.
Um bei gering bewehrten Bauteilen konstruktiv unsinnigen bzw. unterdimensionierten Bauteildicken vorzubeugen, werden außerdem obere Grenzwerte für die zulässige Biegeschlankheit definiert (der kleiner Wert ist maßgebend)[1]:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\frac{l}{d}\right)_{max}= K\cdot 35}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left(\frac{l}{d}\right)_{max}= K^2\cdot \frac{150}{l [m]}}
Ist die zulässige Biegeschlankheit größer als die maximale, ist sie auf diese zu beschränken. Die Maximalwerte der zulässigen Biegeschlankheit dürfen nicht durch weiteren Faktoren modifiziert werden.
Vordimensionierung der Biegeschlankheit

In den Untersuchungen von KRÜGER und MERTZSCH [5] zeigte sich, dass es sinnvoll ist, den Nachweisen der Verformungen über die Biegeschlankheit für Platten und Balken zu trennen. Grund hierfür sind die unterschiedlichen Lagerungsbedingungen und Formen der Beanspruchung bei Platten und Balken. Diese führen bei Platten zu einer deutlich geringeren Rissbildung im Vergleich zu der bei Balken [5]. Beim Grenzwert der Biegeschlankheit für Platten ist die Verkehrslast der maßgebende Faktor, bei dem für Balken der Bewehrungsgrad [5].
Der Nachweis erfolgt mit folgender Gleichung [5]:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle erf \ d =\frac{l_i}{\lambda_i}\cdot k_c}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_i } … Grenzschlankheit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_i=\alpha_i\cdot l_{eff} } … ideelle Stützweite von Balkentragwerken und Flachdecken Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_i=\eta_i\cdot l_{eff} } … ideelle Stützweite von Plattentragwerken
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_c=\left(\frac{f_{ck,0}}{f_{ck}}\right)^\frac{1}{6}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ck,0}=20\frac{N}{mm^2} } … Referenzwert der Betondruckfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ck} \left[\frac{N}{mm^2}\right] } … charakteristische Betondruckfestigkeit
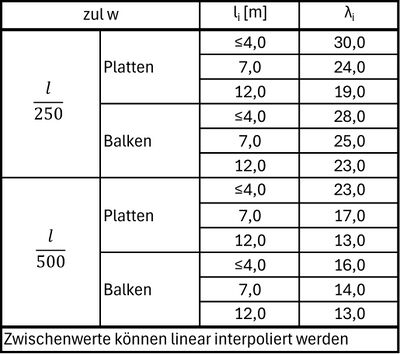
Die dargestellten Tafeln beruhen auf folgenden Annahmen[5]:
DruckfestigkeitFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ck}\geq 25\frac{N}{mm^2}} KriechzahlFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi\leq2,5} Belastung bei PlattenFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q\leq 5,50\frac{kN}{m^2}}
Für eine näherungsweise, analytische Berechnung können folgende Gleichungen verwendet werden[5]:
Balken:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_i=k_1\cdot\left(36,30-2,46\cdot l_i+0,12\cdot l_i^2\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{mit }k_1=\left\{\begin{matrix}1,0\qquad\text{für }\frac{l}{250}\\0,56\qquad\text{für }\frac{l}{500}\end{matrix}\right.}
Platten
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_i=k_2-3,56\cdot l_i+0,15\cdot l_i^2}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{mit }k_2=\left\{\begin{matrix}45,2\qquad\text{für }\frac{l}{250}\\35,2\qquad\text{für }\frac{l}{500}\end{matrix}\right.}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_1=0,168+0,979\cdot k_L-0,283 k_L^2\leq1,0\qquad\qquad} Platte 1 (vgl. Bild) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_2=0,148+0,689\cdot k_L-0,188 k_L^2\qquad\qquad} Platte 2 (vgl. Bild) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_3=0,473+0,200\cdot k_L-0,065 k_L^2\qquad\qquad} Platte 3 (vgl. Bild) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_4=0,103+0,578\cdot k_L-0,162 k_L^2\qquad\qquad} Platte 4 (vgl. Bild)
mitFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad k_L=\frac{L_x}{L_y}\qquad} wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_x \geq L_y}
Quellen
- ↑ 1,0 1,1 1,2 Deutscher Aussschuss für Stahlbeton: Erläuterungen zu DIN EIN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode 2); DAfStb Heft 600
- ↑ Zilch,K., Zehetmaier,G.: Bemessung im konstruktiven Betonbau; 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006
- ↑ 3,0 3,1 DIN EN 1992-1-1, Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2011
- ↑ 4,0 4,1 4,2 Krüger, W. und Mertzsch, O. "Zur Verformungsbegrenzung von überwiegend auf Biegung beanspruchten Stahlbetonquerschnitten" In: Beton- und Stahlbetonbau, Jahrgang 97, Heft 11^(2002), S. 584-589
- ↑ 5,0 5,1 5,2 5,3 5,4 5,5 Krüger, W. und Mertzsch, O. "Verformungsnachweis - Erweiterte Tafeln zur Begrenzung der Biegeschlankheit" In: Stahlbetonbau aktuell (2003)
Seiteninfo
|





