Treppenkonstruktion - Podeste: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
==Besonderheiten der Lastannahmen== | ==Besonderheiten der Lastannahmen== | ||
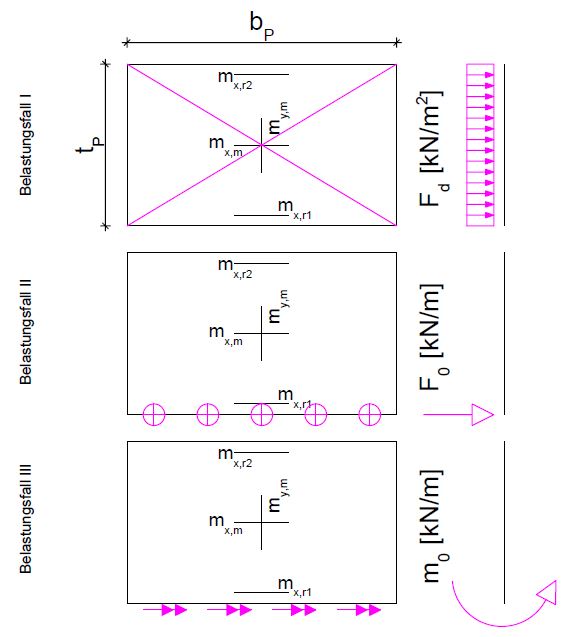
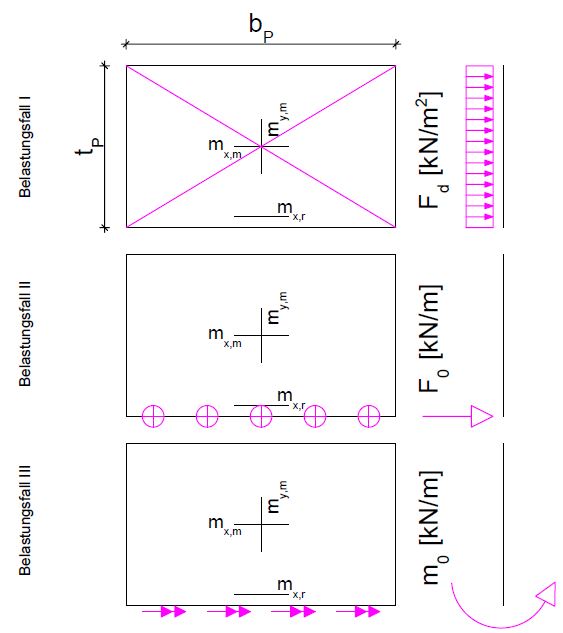
| − | + | Die Berechnung der Podeste wird über das Superpositionsprinzip ausgeführt. Daher gilt für die Lastannahmen, dass jeder Belastungsfall für sich steht. Der erste Belastungsfall ist die Gleichflächenlast <math>F_{d}</math>, welche keine besondere Berechnungsgrundlage benötigt. Der zweite Belastungsfall resultiert aus der Streckenlast <math>F_{0}</math>. Dies ist die am Rand wirkende, aus der Auflagerkraft des Treppenlaufs entstehende Belastung. Der letzte Belastungsfall ist das Einspannungsmoment, welches als Streckenmoment <math>m_{0}</math> am Rand des Podestes angesetzt wird.<ref Name = "AVAK" group="F"></ref> | |
==Auflager== | ==Auflager== | ||
| − | Als Auflager der Podestplatten | + | Als Auflager der Podestplatten werden im allgemeinen Mauerwerk oder Stahlbetonwände verwendet. Um die im folgenden angegeben Tabellen verwenden zu können, darf keine Einspannung der Podeste erfolgen. Sie müssen frei drehbar gelagert werden. |
==statische System== | ==statische System== | ||
| − | Die | + | Die Systembreite <math>b_{P}</math> und -länge <math>t_{P}</math> werden anhand der [[Effektive_Stützweite|effektiven Stützweiten]] angesetzt. Die Berechnungsgrundlage hierfür ist unter dem angegebenen Link zu finden. |
| − | Wie schon bei den Besonderheiten der Lastannahmen beschrieben | + | Wie schon bei den Besonderheiten der Lastannahmen beschrieben, werden die Schnittkräfte der Treppenpodeste mit der Superposition dreier Belastungsfälle errechnet. Welche der Belastungsfälle anzusetzen sind, ist abhängig von der gewählten Treppenanlage. Um die im folgenden angegebenen Tabellen nutzen zu können, müssen die Podeste grundsätzlich frei drehbar gelagert sein. Ist dies nicht der Fall, müssen andere Verfahren der Plattenbemessung herangezogen werden. Im Betonkalender 1980 im Abschnitt Treppen von Köseoglu, S. wurden zwei Tabellen erstellt, mit denen sich Podestplatten mit gegenüberliegenden frei drehbar gelagerten Rändern und Podestplatten mit dreiseitig frei drehbar gelagerten Rändern berechnen lassen. <ref Name = "AVAK" group="F"></ref><ref Name = "Wommelsdorff" group="F">Stahlbetonbau - Bemessung und Konstruktion - Teil 2: Stützen: Sondergebiete des Stahlbetonbaus, Otto Wommelsdorff, Andrej Albert, 2012 Auflage 9</ref> |
:<math> m_{i} = m_{i,I} + m_{i,II} + m_{i,III} </math> | :<math> m_{i} = m_{i,I} + m_{i,II} + m_{i,III} </math> | ||
| Zeile 29: | Zeile 23: | ||
::<math> m_{i,II} </math> - jeweilige Moment an der stelle i der Belastungsvariante II | ::<math> m_{i,II} </math> - jeweilige Moment an der stelle i der Belastungsvariante II | ||
::<math> m_{i,III} </math> - jeweilige Moment an der stelle i der Belastungsvariante III | ::<math> m_{i,III} </math> - jeweilige Moment an der stelle i der Belastungsvariante III | ||
| + | |||
[[Datei:Treppenkonstruktion - Podeste1.JPG|700px|thumb|right|Grafische Darstellung der Belastungsvarianten und der Position der Momente]] | [[Datei:Treppenkonstruktion - Podeste1.JPG|700px|thumb|right|Grafische Darstellung der Belastungsvarianten und der Position der Momente]] | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|+style="text-align:left;"|Tafel zur Schnittgrößen Ermittlung von Podestplatten mit gegenüberliegenden frei drehbar gelagerten Rändern <ref Name = "Köseoglu" group="F">Beton-Kalender, Jahrgang 1980, Band 2, Abschnitt E, Abschnitt Treppen, Köseoglu, S.</ref> <ref Name = "AVAK" group="F">Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5</ref> | |+style="text-align:left;"|Tafel zur Schnittgrößen Ermittlung von Podestplatten mit gegenüberliegenden frei drehbar gelagerten Rändern <ref Name = "Köseoglu" group="F">Beton-Kalender, Jahrgang 1980, Band 2, Abschnitt E, Abschnitt Treppen, Köseoglu, S.</ref> <ref Name = "AVAK" group="F">Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5</ref> | ||
| Zeile 299: | Zeile 295: | ||
|} | |} | ||
| − | Die | + | Die maximale Querkraft tritt in der Regel am Anschlussbereich des Laufs auf. An dieser Stelle findet die Querkraftbemessung statt. Zur Bemessung ist ein fiktiver Streifen mit einer Breite von einem Meter heran zu ziehen. Die maximale Querkraft für gegenläufige Treppenanlagen lässt sich wie folgt berechnen:<ref Name = "AVAK" group="F"></ref> |
| Zeile 313: | Zeile 309: | ||
==Aufbau der Querschnittsform== | ==Aufbau der Querschnittsform== | ||
| − | Die | + | Die normale Querschnittsform ist ein Rechteckquerschnitt der Höhe <math> h_{P} </math>. In der Berechnung wird wie üblich bei der Bemessung von Platten ein Streifen mit einer Breite von <math> 1,0 m </math> verwendet.<ref Name = "AVAK" group="F">Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5</ref> |
| − | |||
==Entwerfen und Bemessen== | ==Entwerfen und Bemessen== | ||
| − | Nach der Ermittlung der Schnittkräfte der Podeste | + | Nach der Ermittlung der Schnittkräfte der Podeste, erfolgt eine Bauteilbemessung.<ref Name = "AVAK" group="F">Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5</ref><ref Name = "Wommelsdorff" group="F">Stahlbetonbau - Bemessung und Konstruktion - Teil 2: Stützen: Sondergebiete des Stahlbetonbaus, Otto Wommelsdorff, Andrej Albert, 2012 Auflage 9</ref> |
| − | Grundlage der Bemessung | + | Grundlage der Bemessung sind der |
| − | Grenzzustand der Tragfähigkeit | + | Grenzzustand der Tragfähigkeit: |
* [[Biegebemessung]] | * [[Biegebemessung]] | ||
* [[Querkraftbemessung]] | * [[Querkraftbemessung]] | ||
| − | Grenzzustand der Gebrauchstauglichkeit | + | und der Grenzzustand der Gebrauchstauglichkeit: |
* [[Begrenzung der Biegeschlankheit|Begrenzung der Verformung (Begrenzung der Biegeschlankheit)]] | * [[Begrenzung der Biegeschlankheit|Begrenzung der Verformung (Begrenzung der Biegeschlankheit)]] | ||
| − | In den Fällen in denen der Treppenlauf über eine Konsole angeschlossen wird sind diese Bereiche extra als versteckter | + | In den Fällen, in denen der Treppenlauf über eine Konsole angeschlossen wird, sind diese Bereiche extra als versteckter Podestträger oder über eine [[Konsolenbemessung]] nachzuweisen. Des Weiteren werden von den Herstellern der Elastomerlager oft Bemessungshilfen nach EC2 in deren Planungsunterlagen gegeben. |
==Beispiele der Handrechnung== | ==Beispiele der Handrechnung== | ||
| − | [[Treppen auf Platten Beispiel 1 - | + | [[Treppen auf Platten, Beispiel 1 - Treppenhaus in einem mehrgeschossigen Wohnhaus, Treppenlauf biegesteif an Podest angeschlossen]] |
| + | ==''Quellen''== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
:''Fachliteratur'' | :''Fachliteratur'' | ||
<references group="F" /><br /> | <references group="F" /><br /> | ||
<br /> | <br /> | ||
| − | + | ||
| − | |||
| − | |||
Aktuelle Version vom 11. November 2019, 16:58 Uhr
Besonderheiten der Lastannahmen
Die Berechnung der Podeste wird über das Superpositionsprinzip ausgeführt. Daher gilt für die Lastannahmen, dass jeder Belastungsfall für sich steht. Der erste Belastungsfall ist die Gleichflächenlast Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{d}} , welche keine besondere Berechnungsgrundlage benötigt. Der zweite Belastungsfall resultiert aus der Streckenlast Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{0}} . Dies ist die am Rand wirkende, aus der Auflagerkraft des Treppenlaufs entstehende Belastung. Der letzte Belastungsfall ist das Einspannungsmoment, welches als Streckenmoment Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{0}} am Rand des Podestes angesetzt wird.[F 1]
Auflager
Als Auflager der Podestplatten werden im allgemeinen Mauerwerk oder Stahlbetonwände verwendet. Um die im folgenden angegeben Tabellen verwenden zu können, darf keine Einspannung der Podeste erfolgen. Sie müssen frei drehbar gelagert werden.
statische System
Die Systembreite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{P}} und -länge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_{P}} werden anhand der effektiven Stützweiten angesetzt. Die Berechnungsgrundlage hierfür ist unter dem angegebenen Link zu finden.
Wie schon bei den Besonderheiten der Lastannahmen beschrieben, werden die Schnittkräfte der Treppenpodeste mit der Superposition dreier Belastungsfälle errechnet. Welche der Belastungsfälle anzusetzen sind, ist abhängig von der gewählten Treppenanlage. Um die im folgenden angegebenen Tabellen nutzen zu können, müssen die Podeste grundsätzlich frei drehbar gelagert sein. Ist dies nicht der Fall, müssen andere Verfahren der Plattenbemessung herangezogen werden. Im Betonkalender 1980 im Abschnitt Treppen von Köseoglu, S. wurden zwei Tabellen erstellt, mit denen sich Podestplatten mit gegenüberliegenden frei drehbar gelagerten Rändern und Podestplatten mit dreiseitig frei drehbar gelagerten Rändern berechnen lassen. [F 1][F 2]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{i} = m_{i,I} + m_{i,II} + m_{i,III} }
- mit:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{i} } - Moment nach dem Bemessen wird
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{i,I} } - jeweilige Moment an der stelle i der Belastungsvariante I
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{i,II} } - jeweilige Moment an der stelle i der Belastungsvariante II
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{i,III} } - jeweilige Moment an der stelle i der Belastungsvariante III
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Belastungsvariante | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac {t_{P}}{b_{P} } } | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi } | ||||||||||
| 1 | I | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,m} = \frac{F_{d} \cdot b_{P}^{2}}{8} } | ||||||||
| 2 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{y,m} = 0,2 \cdot m_{x,m} } | |||||||||
| 3 | II | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,m} = \frac{F_{0} \cdot b_{P}}{\chi} } | 2,39 | 3,23 | 4,05 | 4,88 | 5,81 | 6,81 | 7,41 | 9,00 |
| 4 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{y,m} = - \frac{F_{0} \cdot b_{P}}{\chi} } | 38,5 | 31,3 | 27,8 | 26,4 | 25,7 | 26,4 | 27,1 | 29,8 | |
| 5 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r1} = \frac{F_{0} \cdot b_{P}}{\chi} } | 2,19 | 2,75 | 3,17 | 3,45 | 3,65 | 3,81 | 3,88 | 3,96 | |
| 6 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r2} = \frac{F_{0} \cdot b_{P}}{\chi} } | 2,63 | 3,79 | 5,18 | 6,85 | 9,00 | 12,1 | 15,6 | 20,9 | |
| 7 | III | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,m} = - \frac{m_{0}}{\chi} } | 200 | 66,7 | 38,5 | 26,4 | 21,3 | 18,6 | 16,9 | 16,1 |
| 8 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{y,m} = - \frac{m_{0}}{\chi} } | 2,08 | 2,29 | 2,58 | 3,00 | 3,57 | 4,37 | 5,35 | 6,61 | |
| 9 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r1} = \frac{m_{0}}{\chi} } | 3,85 | 3,65 | 3,49 | 3,34 | 3,24 | 3,16 | 3,10 | 3,07 | |
| 10 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r2} = - \frac{m_{0}}{\chi} } | 4,18 | 4,55 | 5,08 | 5,96 | 7,15 | 8,55 | 10,4 | 13,2 | |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi}
= Wert in der Tabelle
| ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Belastungsvariante | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac {t_{P}}{b_{P} } } | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi } | ||||||||||
| 1 | I | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,m} = \frac{F_{d} \cdot t_{P}^{2}}{\chi} } | 7,88 | 8,04 | 8,46 | 9,11 | 9,97 | 11,0 | 12,2 | 13,6 |
| 2 | 8,92 | 10,5 | 13,0 | 16,5 | 21,2 | 27,5 | 35,7 | 46,1 | ||
| 3 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r} = \frac{F_{d} \cdot t_{P}^{2}}{\chi} } | 4,12 | 4,41 | 4,89 | 5,53 | 6,34 | 7,32 | 8,46 | 9,77 | |
| 4 | II | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,m} = \frac{F_{d} \cdot b_{P}}{\chi} } | 12,6 | 10,5 | 9,60 | 9,20 | 9,40 | 9,60 | 10,2 | 10,9 |
| 5 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{y,m} = - \frac{F_{d} \cdot b_{P}}{\chi} } | 200 | 91,0 | 52,5 | 40,1 | 33,2 | 29,4 | 26,9 | 25,0 | |
| 6 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r} = \frac{F_{d} \cdot b_{P}}{\chi} } | 6,90 | 5,60 | 4,90 | 4,50 | 4,30 | 4,20 | 4,10 | 4,10 | |
| 7 | III | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{y,m} = \frac{m_{0}}{\chi} } | 4,60 | 5,70 | 7,90 | 12,5 | 35,0 | 100 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \infty} | -31 |
| 8 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{y,m} = - \frac{m_{0}}{\chi} } | 2,10 | 2,20 | 2,50 | 3,10 | 4,00 | 5,10 | 6,50 | 8,00 | |
| 9 | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m_{x,r} = \frac{m_{0}}{\chi} } | 2,20 | 2,35 | 2,50 | 2,65 | 2,74 | 2,80 | 2,85 | 2,90 | |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi}
= Wert in der Tabelle
| ||||||||||
Die maximale Querkraft tritt in der Regel am Anschlussbereich des Laufs auf. An dieser Stelle findet die Querkraftbemessung statt. Zur Bemessung ist ein fiktiver Streifen mit einer Breite von einem Meter heran zu ziehen. Die maximale Querkraft für gegenläufige Treppenanlagen lässt sich wie folgt berechnen:[F 1]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed,max} = F_{d} \cdot \frac{b_{P}}{2} + F_{0} \cdot \frac{2 \cdot b_{L}}{2} }
- mit:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed,max} } - Bemessungswert der einwirkenden Querkraft
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{d} } - gesamte Gleichflächenlast aus Eigen- und Verkehrslast
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{P} } - die effektive Stützweite
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{0} } - Randlast aus der Auflagerkraft des Treppenlaufs
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{L} } - Breite des Treppenlaufs
Aufbau der Querschnittsform
Die normale Querschnittsform ist ein Rechteckquerschnitt der Höhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{P} } . In der Berechnung wird wie üblich bei der Bemessung von Platten ein Streifen mit einer Breite von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,0 m } verwendet.[F 1]
Entwerfen und Bemessen
Nach der Ermittlung der Schnittkräfte der Podeste, erfolgt eine Bauteilbemessung.[F 1][F 2]
Grundlage der Bemessung sind der
Grenzzustand der Tragfähigkeit:
und der Grenzzustand der Gebrauchstauglichkeit:
In den Fällen, in denen der Treppenlauf über eine Konsole angeschlossen wird, sind diese Bereiche extra als versteckter Podestträger oder über eine Konsolenbemessung nachzuweisen. Des Weiteren werden von den Herstellern der Elastomerlager oft Bemessungshilfen nach EC2 in deren Planungsunterlagen gegeben.
Beispiele der Handrechnung
Quellen
- Fachliteratur
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5
- ↑ 2,0 2,1 Stahlbetonbau - Bemessung und Konstruktion - Teil 2: Stützen: Sondergebiete des Stahlbetonbaus, Otto Wommelsdorff, Andrej Albert, 2012 Auflage 9
- ↑ 3,0 3,1 Beton-Kalender, Jahrgang 1980, Band 2, Abschnitt E, Abschnitt Treppen, Köseoglu, S.
Seiteninfo
|