Treppenkonstruktion – Treppen auf Platten: Unterschied zwischen den Versionen
| (16 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
====Besonderheiten der Lastannahmen==== | ====Besonderheiten der Lastannahmen==== | ||
| − | Für Treppen auf Platten sind die Flächenlasten <math> | + | Für Treppen auf Platten sind die Flächenlasten <math> g_{k} </math> auf der Länge des Treppenlaufs im Grundriss anzusetzen. Die ständigen Lasten werden ebenso auf den Grundriss bezogen. Dazu gehören die Einwirkungen aus dem Bodenbelag wie aus dem Putz an der Unterweite des Treppenlaufs. Aus diesem Grund gelten auch für Eigenlasten des sägeartigen Querschnittanteils der Treppe folgende Gleichungen: <ref Name = "Köseoglu" group="F">Beton-Kalender, Jahrgang 1980, Band 2, Abschnitt E, Abschnitt Treppen, Köseoglu, S.</ref> <ref Name = "Wommelsdorff" group="F">Stahlbetonbau - Bemessung und Konstruktion - Teil 2: Stützen: Sondergebiete des Stahlbetonbaus, Otto Wommelsdorff, Andrej Albert, 2012 Auflage 9</ref>: |
| − | :<math> | + | :<math> g_{k} = g^{*}_{k} + g^{**}_{k} </math> |
:mit: | :mit: | ||
| − | ::<math> | + | ::<math> g_{k}</math> -gesamtes charakteristisches Eigengewicht |
| − | ::<math> | + | ::<math> g^{*}_{k} </math> - charakteristischer Wert der Platteneigenlast |
| − | ::<math> | + | ::<math> g^{**}_{k} </math> - charakteristischer Wert der Stufeneigenlast |
| − | Der charakteristische Wert der Stufeneigenlast <math> | + | Der charakteristische Wert der Stufeneigenlast <math> g^{**}_{k}</math> lässt sich über die folgende Gleichung lösen <ref Name = "Wommelsdorff" group="F"></ref>: |
| − | :<math> | + | :<math> g^{**}_{k} = \frac{s \cdot \gamma_{2}}{2} </math> |
:mit: | :mit: | ||
::<math> s </math> - Steigung | ::<math> s </math> - Steigung | ||
::<math>\gamma_{2}</math> - <math> 24 \frac{kN}{m^{3}} </math> Wichte für unbewehrten Beton | ::<math>\gamma_{2}</math> - <math> 24 \frac{kN}{m^{3}} </math> Wichte für unbewehrten Beton | ||
| − | Der charakteristische Wert der Platteneigenlast <math> | + | Der charakteristische Wert der Platteneigenlast <math> g^{*}_{k} </math> hingegen lässt sich so berechnen <ref Name = "Wommelsdorff" group="F"></ref>: |
| − | :<math> | + | :<math> g^{*}_{k} = \frac{ h \cdot \gamma_{1}}{cos(\alpha)} </math> |
:mit: | :mit: | ||
::<math>\alpha</math> - Steigungswinkel | ::<math>\alpha</math> - Steigungswinkel | ||
| Zeile 32: | Zeile 26: | ||
| − | Die Lagerung der Treppenanlage kann auf verschiedene Wege erfolgen. Es ist möglich, die Kräfte in die Podestplatte, Deckenplatte, in den versteckten oder sichtbaren Podestträger oder in das anstehende Mauerwerk einzuleiten. Für die Spannweite der Platte gelten die Entfernungen der Auflagermitten im Grundriss. | + | Die Lagerung der Treppenanlage kann auf verschiedene Wege erfolgen. Es ist möglich, die Kräfte in die Podestplatte, Deckenplatte, in den versteckten oder sichtbaren Podestträger oder in das anstehende Mauerwerk einzuleiten. Für die Spannweite der Platte gelten die Entfernungen der Auflagermitten im Grundriss.<ref Name = "Köseoglu" group="F">Beton-Kalender, Jahrgang 1980, Band 2, Abschnitt E, Abschnitt Treppen, Köseoglu, S.</ref><ref Name = "Fuchssteiner" group="F">Beton-Kalender, Jahrgang 2000, Band 2, Abschnitt Treppen, W. Fuchsteiner</ref> |
| Zeile 39: | Zeile 33: | ||
====statische System==== | ====statische System==== | ||
| − | =====Statisch bestimmte Systeme | + | =====Statisch bestimmte Systeme===== |
Für die Wahl des statischen Systems wird hier ein grafischer Überblick über die Möglichkeiten, wie die Kräfte innerhalb des Treppensystems abgetragen werden können, gegeben. | Für die Wahl des statischen Systems wird hier ein grafischer Überblick über die Möglichkeiten, wie die Kräfte innerhalb des Treppensystems abgetragen werden können, gegeben. | ||
[[Datei:Treppen_auf_Platten_statisches_System.png|500px|thumb|right|Tragsystemvariante (a) <ref Name = "Wommelsdorff" group="F"></ref>]] | [[Datei:Treppen_auf_Platten_statisches_System.png|500px|thumb|right|Tragsystemvariante (a) <ref Name = "Wommelsdorff" group="F"></ref>]] | ||
| − | In Tragsystemvariante (a) wird das System einachsig gespannt auf dem anstehenden Mauerwerk oder den betonierten Wänden gelagert. Für die Ermittlung der Schnittkräfte gelten keine speziellen Formeln. | + | In Tragsystemvariante (a) wird das System einachsig gespannt auf dem anstehenden Mauerwerk oder den betonierten Wänden gelagert. Für die Ermittlung der Schnittkräfte gelten keine speziellen Formeln.<ref Name = "Wommelsdorff" group="F"></ref> |
| Zeile 54: | Zeile 48: | ||
[[Datei:Treppen_auf_Platten_statisches_System2.png|500px|thumb|right|Tragsystemvariante (b) <ref Name = "Wommelsdorff" group="F"></ref>]] | [[Datei:Treppen_auf_Platten_statisches_System2.png|500px|thumb|right|Tragsystemvariante (b) <ref Name = "Wommelsdorff" group="F"></ref>]] | ||
| − | Bei der Wahl des statischen Systems nach der Variante (b) werden die Lasten der Treppenläufe auf einen Streifen der Breite <math>b_{eff }</math> auf das Podest verteilt. Die Breite <math>b_{eff }</math> ist frei wählbar, solange der Gleichgewichtszustand des Gesamtsystems eingehalten wird. Dieses System findet Anwendung bei Treppenläufen in Fertigteilbauweise. Der Lauf wird über Konsolen, ausgestattet mit Elastomerlagern, gelagert und leitet über dieses Lager die Kräfte an die Podeste weiter. | + | Bei der Wahl des statischen Systems nach der Variante (b) werden die Lasten der Treppenläufe auf einen Streifen der Breite <math>b_{eff }</math> auf das Podest verteilt. Die Breite <math>b_{eff }</math> ist frei wählbar, solange der Gleichgewichtszustand des Gesamtsystems eingehalten wird. Dieses System findet Anwendung bei Treppenläufen in Fertigteilbauweise. Der Lauf wird über Konsolen, ausgestattet mit Elastomerlagern, gelagert und leitet über dieses Lager die Kräfte an die Podeste weiter.<ref Name = "Wommelsdorff" group="F"></ref> |
<br /> | <br /> | ||
Zur Hilfe bei der Wahl der Breite <math>b_{eff }</math> wird in der Literatur folgende Gleichung genannt: | Zur Hilfe bei der Wahl der Breite <math>b_{eff }</math> wird in der Literatur folgende Gleichung genannt: | ||
| Zeile 68: | Zeile 62: | ||
[[Datei:Treppen_auf_Platten_statisches_System3.png|500px|thumb|right|Tragsystemvariante (c) <ref Name = "Wommelsdorff" group="F"></ref>]] | [[Datei:Treppen_auf_Platten_statisches_System3.png|500px|thumb|right|Tragsystemvariante (c) <ref Name = "Wommelsdorff" group="F"></ref>]] | ||
| − | In der Variante (c) wird ein Stützmoment an die Ränder des Laufs angesetzt. Dies tritt aber nur auf, wenn der Lauf monolithisch an die Podeste angeschlossen ist. Im Falle des Verbaus einer [[Treppenkonstruktion#Sch.C3.B6ck_Treppentronsolen|Tronsole]] wird von einer freidrehbaren Lagerung ausgegangen. Falls sich dennoch für dieses System entschieden wird, empfiehlt die Literatur statt einer genauen Berechnung, die Schnittkräfte der Treppenläufe nach folgenden Formeln zu berechnen: | + | In der Variante (c) wird ein Stützmoment an die Ränder des Laufs angesetzt. Dies tritt aber nur auf, wenn der Lauf monolithisch an die Podeste angeschlossen ist. Im Falle des Verbaus einer [[Treppenkonstruktion#Sch.C3.B6ck_Treppentronsolen|Tronsole]] wird von einer freidrehbaren Lagerung ausgegangen. Falls sich dennoch für dieses System entschieden wird, empfiehlt die Literatur statt einer genauen Berechnung, die Schnittkräfte der Treppenläufe nach folgenden Formeln zu berechnen<ref Name = "Wommelsdorff" group="F"></ref>: |
:<math> C_{Ed} =f_{d} \cdot \frac{l_{L}}{2} </math> | :<math> C_{Ed} =f_{d} \cdot \frac{l_{L}}{2} </math> | ||
| Zeile 81: | Zeile 75: | ||
=====Statisch unbestimmte Systeme===== | =====Statisch unbestimmte Systeme===== | ||
| − | Es ist auch möglich mit Zwischenlagern, beispielweise an Übergang zwischen Lauf und Podest, statisch unbestimmte Treppenläufe herzustellen. Die Schnittkräfte sind dabei über die bekannten Methoden zu ermitteln. In der Literatur wird Hierbei Meist das Kraftgrößenverfahren verwendet.Dieses Verfahren findet in der Regel jedoch keine Anwendung, da diese Systeme in statisch bestimmte Teilsysteme aufgeteilt werden können. Dabei ist darauf zu achten, dass die Gleichgewichtszustände am Gesamtsystem eingehalten werden. | + | Es ist auch möglich mit Zwischenlagern, beispielweise an Übergang zwischen Lauf und Podest, statisch unbestimmte Treppenläufe herzustellen. Die Schnittkräfte sind dabei über die bekannten Methoden zu ermitteln. In der Literatur wird Hierbei Meist das Kraftgrößenverfahren verwendet. Dieses Verfahren findet in der Regel jedoch keine Anwendung, da diese Systeme in statisch bestimmte Teilsysteme aufgeteilt werden können. Dabei ist darauf zu achten, dass die Gleichgewichtszustände am Gesamtsystem eingehalten werden. |
====Aufbau der Querschnittsform==== | ====Aufbau der Querschnittsform==== | ||
Im Allgemeinen befindet sich in diesem Tragsystem unter den Treppenstufen eine tragende Platte. Diese leitet die Kräfte, abhängig vom gewählten statischen System, in die jeweiligen Bauteile ein. | Im Allgemeinen befindet sich in diesem Tragsystem unter den Treppenstufen eine tragende Platte. Diese leitet die Kräfte, abhängig vom gewählten statischen System, in die jeweiligen Bauteile ein. | ||
| + | |||
| + | Die normale Querschnittsform ist ein Rechteckquerschnitt der Höhe h_{L}. In der Berechnung wird wie üblich bei der Bemessung von Platten ein Streifen mit einer Breite von 1,0 m verwendet.<ref Name = "Wommelsdorff" group="F"></ref> | ||
====Entwerfen und Bemessen==== | ====Entwerfen und Bemessen==== | ||
| Zeile 96: | Zeile 92: | ||
* [[Querkraftbemessung]] | * [[Querkraftbemessung]] | ||
* [[Sicherstellung des duktilen Bauteilverhaltens]] | * [[Sicherstellung des duktilen Bauteilverhaltens]] | ||
| − | * [[ | + | * [[Treppenkonstruktion_-_Podeste|Plattenbemessung Podestplatten]] |
| − | |||
Die Bereiche der Diskontinuität sind die Auflagerkonsolen Grundlage hierzu ist: | Die Bereiche der Diskontinuität sind die Auflagerkonsolen Grundlage hierzu ist: | ||
| Zeile 105: | Zeile 100: | ||
* [[Konsolen Bemessung]] | * [[Konsolen Bemessung]] | ||
| − | Des Weiteren werden biegesteife Verbindungen zwischen dem Lauf im Steigungswinkel und den nahezu in der Waage angeordneten Podesten mit Hilfe von konstruktiven Bewehrungsregeln gestaltet. Hierbei ist darauf zu achten, dass Umlenkkräfte nicht um einspringende Ecken geführt werden dürfen. Zudem müssen Arbeitsfugen festgelegt werden, um die Bewehrungsführung daraufhin abzustimmen. | + | Des Weiteren werden biegesteife Verbindungen zwischen dem Lauf im Steigungswinkel und den nahezu in der Waage angeordneten Podesten mit Hilfe von konstruktiven Bewehrungsregeln gestaltet. Hierbei ist darauf zu achten, dass Umlenkkräfte nicht um einspringende Ecken geführt werden dürfen. Zudem müssen Arbeitsfugen festgelegt werden, um die Bewehrungsführung daraufhin abzustimmen.<ref Name = "AVAK" group="F">Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5</ref><ref Name = "Wommelsdorff" group="F"></ref> |
====Beispiele der Handrechnung==== | ====Beispiele der Handrechnung==== | ||
| + | [[Treppen auf Platten, Beispiel 1 - Treppenhaus in einem mehrgeschossigen Wohnhaus, Treppenlauf biegesteif an Podest angeschlossen]] | ||
====Softwarelösung für die Tragwerksplanung==== | ====Softwarelösung für die Tragwerksplanung==== | ||
| Zeile 117: | Zeile 113: | ||
=''Quellen''= | =''Quellen''= | ||
| − | + | ||
| − | |||
| − | |||
:''Fachliteratur'' | :''Fachliteratur'' | ||
<references group="F" /><br /> | <references group="F" /><br /> | ||
<br /> | <br /> | ||
| − | + | ||
| − | |||
| − | |||
{{Seiteninfo | {{Seiteninfo | ||
Aktuelle Version vom 11. November 2019, 17:01 Uhr
Besonderheiten der Lastannahmen
Für Treppen auf Platten sind die Flächenlasten auf der Länge des Treppenlaufs im Grundriss anzusetzen. Die ständigen Lasten werden ebenso auf den Grundriss bezogen. Dazu gehören die Einwirkungen aus dem Bodenbelag wie aus dem Putz an der Unterweite des Treppenlaufs. Aus diesem Grund gelten auch für Eigenlasten des sägeartigen Querschnittanteils der Treppe folgende Gleichungen: [F 1] [F 2]:
- mit:
- -gesamtes charakteristisches Eigengewicht
- - charakteristischer Wert der Platteneigenlast
- - charakteristischer Wert der Stufeneigenlast
Der charakteristische Wert der Stufeneigenlast lässt sich über die folgende Gleichung lösen [F 2]:
- mit:
- - Steigung
- - Wichte für unbewehrten Beton
Der charakteristische Wert der Platteneigenlast hingegen lässt sich so berechnen [F 2]:
- mit:
- - Steigungswinkel
- - Wichte für Stahlbeton
- - Querschnittshöhe der Platte
Auflager
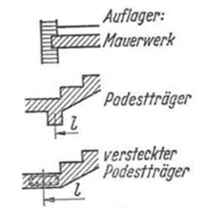
Die Lagerung der Treppenanlage kann auf verschiedene Wege erfolgen. Es ist möglich, die Kräfte in die Podestplatte, Deckenplatte, in den versteckten oder sichtbaren Podestträger oder in das anstehende Mauerwerk einzuleiten. Für die Spannweite der Platte gelten die Entfernungen der Auflagermitten im Grundriss.[F 1][F 3]
statische System
Statisch bestimmte Systeme
Für die Wahl des statischen Systems wird hier ein grafischer Überblick über die Möglichkeiten, wie die Kräfte innerhalb des Treppensystems abgetragen werden können, gegeben.
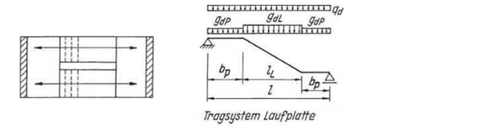
In Tragsystemvariante (a) wird das System einachsig gespannt auf dem anstehenden Mauerwerk oder den betonierten Wänden gelagert. Für die Ermittlung der Schnittkräfte gelten keine speziellen Formeln.[F 2]
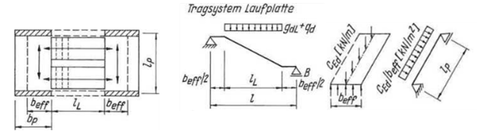
Bei der Wahl des statischen Systems nach der Variante (b) werden die Lasten der Treppenläufe auf einen Streifen der Breite auf das Podest verteilt. Die Breite ist frei wählbar, solange der Gleichgewichtszustand des Gesamtsystems eingehalten wird. Dieses System findet Anwendung bei Treppenläufen in Fertigteilbauweise. Der Lauf wird über Konsolen, ausgestattet mit Elastomerlagern, gelagert und leitet über dieses Lager die Kräfte an die Podeste weiter.[F 2]
Zur Hilfe bei der Wahl der Breite wird in der Literatur folgende Gleichung genannt:
Wobei:
- - Podestbreite
Wenn die Lasten gemäß der beschriebenen Breite b_{eff} angesetzt werden, erfolgt die Schnittgrößenermittlung für diesen Streifen der Podestplatte für eine einachsig gespannte Platte.
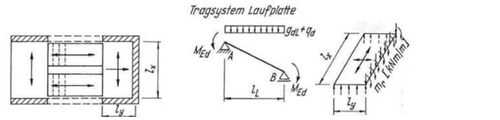
In der Variante (c) wird ein Stützmoment an die Ränder des Laufs angesetzt. Dies tritt aber nur auf, wenn der Lauf monolithisch an die Podeste angeschlossen ist. Im Falle des Verbaus einer Tronsole wird von einer freidrehbaren Lagerung ausgegangen. Falls sich dennoch für dieses System entschieden wird, empfiehlt die Literatur statt einer genauen Berechnung, die Schnittkräfte der Treppenläufe nach folgenden Formeln zu berechnen[F 2]:
Wobei :
- - Belastung des Treppenlaufes
- - Auflagerkraft des Treppenlaufes
- - Bemessungsmoment des Treppenlaufes im Feld bzw. am Podestrand
Statisch unbestimmte Systeme
Es ist auch möglich mit Zwischenlagern, beispielweise an Übergang zwischen Lauf und Podest, statisch unbestimmte Treppenläufe herzustellen. Die Schnittkräfte sind dabei über die bekannten Methoden zu ermitteln. In der Literatur wird Hierbei Meist das Kraftgrößenverfahren verwendet. Dieses Verfahren findet in der Regel jedoch keine Anwendung, da diese Systeme in statisch bestimmte Teilsysteme aufgeteilt werden können. Dabei ist darauf zu achten, dass die Gleichgewichtszustände am Gesamtsystem eingehalten werden.
Aufbau der Querschnittsform
Im Allgemeinen befindet sich in diesem Tragsystem unter den Treppenstufen eine tragende Platte. Diese leitet die Kräfte, abhängig vom gewählten statischen System, in die jeweiligen Bauteile ein.
Die normale Querschnittsform ist ein Rechteckquerschnitt der Höhe h_{L}. In der Berechnung wird wie üblich bei der Bemessung von Platten ein Streifen mit einer Breite von 1,0 m verwendet.[F 2]
Entwerfen und Bemessen
Nachdem das System durch die vorangegangenen Punkte bestimmt wurde, wird in dem Fall der Treppe auf einer Platte das komplizierte statische System dieser Treppenanlage in die D-Bereiche (D = Diskontinuität), die mit der Theorie der Stabtragwerksmodelle berechnet werden, bzw. in die B-Bereiche (B = Balken oder Bernoulli), die als Plattentragwerk gelten, idealisiert. Diese Vorgehensweise wird auch von den üblichen Softwarelösungen für die Tragwerksplanung verwendet.
Für die Bauteilbereiche, in denen die Bernoulli-Hypothese gilt, kann der Treppenlauf als ebenes System behandelt werden, da dieser in Gedanken in die Ebene projiziert wurde. Der B-Bereich einer Treppe unterscheidet sich somit auch nicht mehr von einer Stahlbetonplatte. Daher werden in diesem Bereich nach üblichen Verfahren die Schnittkräfte ermittelt und nach diesen bemessen und konstruiert. [F 3][F 2]
Grundlage dieser Bemessung ist:
- Biegebemessung
- Querkraftbemessung
- Sicherstellung des duktilen Bauteilverhaltens
- Plattenbemessung Podestplatten
Die Bereiche der Diskontinuität sind die Auflagerkonsolen Grundlage hierzu ist:
Des Weiteren werden biegesteife Verbindungen zwischen dem Lauf im Steigungswinkel und den nahezu in der Waage angeordneten Podesten mit Hilfe von konstruktiven Bewehrungsregeln gestaltet. Hierbei ist darauf zu achten, dass Umlenkkräfte nicht um einspringende Ecken geführt werden dürfen. Zudem müssen Arbeitsfugen festgelegt werden, um die Bewehrungsführung daraufhin abzustimmen.[F 4][F 2]
Beispiele der Handrechnung
Softwarelösung für die Tragwerksplanung
S230.de Gerader Stahlbeton Treppenlauf
S231.de Gerader Stahlbeton Treppenlauf
S232.de Gerader Stahlbeton Treppenlauf
Quellen
- Fachliteratur
- ↑ 1,0 1,1 Beton-Kalender, Jahrgang 1980, Band 2, Abschnitt E, Abschnitt Treppen, Köseoglu, S.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 Stahlbetonbau - Bemessung und Konstruktion - Teil 2: Stützen: Sondergebiete des Stahlbetonbaus, Otto Wommelsdorff, Andrej Albert, 2012 Auflage 9
- ↑ 3,0 3,1 3,2 Beton-Kalender, Jahrgang 2000, Band 2, Abschnitt Treppen, W. Fuchsteiner
- ↑ Stahlbetonbau in Beispielen - Teil 2: Bemessung von Flächentragwerken nach EC 2 - Konstruktionspläne für Stahlbetonbauteile, Ralf Avak, René Conchon, Markus Aldejohann 2017 Auflage 5
Seiteninfo
|






















