Mitwirkende Plattenbreite: Unterschied zwischen den Versionen

Aktuelle Version vom 11. Januar 2023, 22:48 Uhr

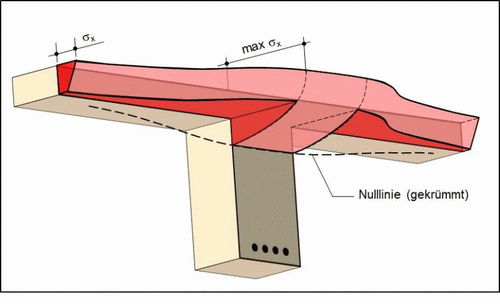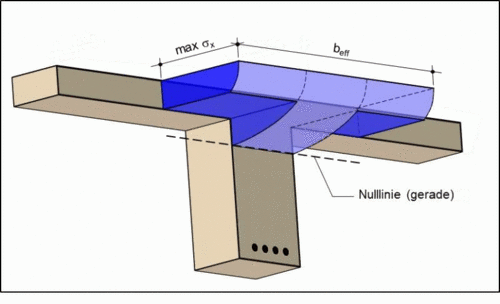
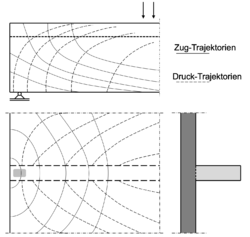
Mitwirkende Plattenbreite - realer/ideeller Spannungsverlauf in der Platte

Die mitwirkende Plattenbreite (b_eff) ist eine Ersatzbreite, mit der sich der reale Verlauf der Druckspannungen innerhalb der Platte eines Plattenbalkens, unter Annahme einer rechteckigen Druckspannungsverteilung, annähern lässt. Die Berechnung im normalen Hochbau erfolgt mittels Näherungsformel aus dem Eurocode 2, bei Sonderbauten wie Brücken kann eine genauere, computergestützte Berechnung sinnvoll sein.

Einleitung

Plattenbalken sind Balken mit einem T-förmigen Querschnitt. In der Biegezugzone des Balkens befindet sich die Längsbewehrung und nimmt die Zugkräfte auf. Im Biegedruckbereich wirkt beim monolithischen Plattenbalken neben dem Balkenquerschnitt auch ein bestimmter Bereich der Platte mit und nimmt die Druckspannungen auf. Diese Breite wird als mitwirkende Plattenbreite (b_eff) bezeichnet. Eine genaue Berechnung ist äußerst umständlich, da verschiedene Faktoren einen Einfluss auf die Größe haben:

Querschnittsabmessungen
- Dicke der Platte
- Höhe des Balkens
Schub- und Biegesteifigkeit der Platte
Art der Belastung
- Einzellasten
- gleichmäßig verteilte Lasten
Art des Systems
- Spannweite
- Abstand zwischen den Stegen

Der Eurocode 2 ^[1] enthält eine Näherungsformel für die mitwirkende Plattenbreite, die für den normalen Hochbau ausreichend genaue Ergebnisse liefert. Ausreichend genau bedeutet hier, dass das Ergebnis auf der sicheren Seite liegt und eine genaue Berechnung oft nicht wirtschaftlicher im Vergleich zur Nutzung der Näherungsformel wäre.

Berechnungsgrundlagen

Anwendung

Gebrauch findet die mitwirkende Plattenbreite vorwiegend bei der Biegebemessung von Plattenbalken. Eine Vergrößerung der mitwirkenden Plattenbreite führt bei sonst gleichen Bedingungen

zu einer Erhöhung der aufnehmbaren Druckkraft in der Druckzone
zu einer Vergrößerung des Hebelarmes der inneren Kräfte und damit zu einer Verringerung der erforderlichen Biegebewehrung (Auswirkung eher gering)

Des Weiteren wird die mitwirkende Plattenbreite als Grundlage für die Ermittlung der Anschlussbewehrung für den Anschluss von Druck-und Zuggurten verwendet. Eine Vergrößerung der mitwirkenden Plattenbreite führt hier zu einer Erhöhung der Menge und Länge der Anschlussbewehrung.
Darüber hinaus wird die mitwirkende Plattenbreite als Basis für die mögliche Verteilungsbreite der Biegezugbewehrung in den Gurten von Plattenbalken über Zwischenauflagern verwendet.

Berechnung nach Eurocode 2-1-1

Mitwirkende Plattenbreite - mit Bezeichnungen nach EC 2

Für Nachweise im Grenzzustand der Tragfähigkeit und der Gebrauchstauglichkeit darf die mitwirkende Plattenbreite wie folgt ermittelt werden:

b_{eff}=\sum b_{eff,i}+b_{w}\leq b

mit:

b_{eff,i}={min}{\begin{cases}0{,}2\cdot b_{i}+0{,}1\cdot l_{0}\\0{,}2\cdot l_{0}\\b_{i}\end{cases}}

wobei:

b_eff...	Mitwirkende Plattenbreite
b_eff,i...	Mitwirkende einseitige Plattenbreite (rechts/links)
b_i...	Tatsächlich vorhandene einseitige Plattenbreite
b_w...	Stegbreite
l₀...	Wirksame Stützweite (Abstand der Momentennullpunkte)

Ein genauer Berechungsablauf wird in Mitwirkende Plattenbreite (Bsp.) aufgezeigt.
Die Ermittlung des Abstandes der Momentennullpunkte erfolgt vereinfacht nach den Formeln in der angegebenen Darstellung.

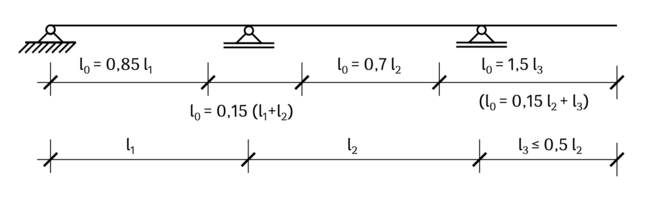
Die Angaben gelten bei annähernd gleichen Steifigkeiten und annähernd gleicher Belastung für ein Stützweitenverhältnis benachbarter Felder im Bereich von $0,8<l_{1}/l_{2}<1,25$ . Für kurze Kragarme ( $l_{3}/l_{2}<0,5$ ) gilt $l_{0}=1,5\cdot l_{3}$ , ansonsten $l_{0}=0,15\cdot l_{2}+l_{3}$ . ^[2]

Wissenschaftlicher Hintergrund

Die Forschung zur mitwirkenden Plattenbreite hat bereits zum Anfang des 20. Jahrhunderts begonnen (siehe Mitwirkende Plattenbreite - Geschichtliche Entwicklung und normative Regeln) und sich von sehr groben Formeln zu einer Näherungsberechnung entwickelt, die viele Faktoren berücksichtigt. Jedoch ist der Zweck dieser Näherung eben dieser - ein kompliziertes System vereinfacht darzustellen. Einige Faktoren sind heute innerhalb der Näherung klar definiert und zu anderen gibt es umfassende wissenschaftliche Arbeiten, deren Erkenntnisse jedoch nur teilweise in den Normen berücksichtigt werden. Die wichtigsten dieser wissenschaftlichen Erkenntnisse bezüglich der mitwirkenden Plattenbreite werden folgend kurz zusammengefasst.

Berechnung nach Scheibentheorie

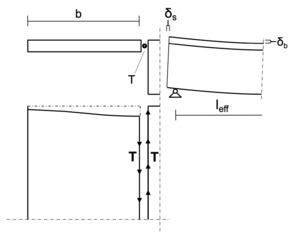
Mitwirkung der Platte über eine Schubkraft T entlang der Verbindungsfuge (Darstellung nach Brendel)^[3]

Die Scheibentheorie befasst sich mit der Berechnung von Spannungen und Verformungen innerhalb von Scheibenelementen. Nach dieser Theorie wird ein Plattenbalken in zwei Plattenelemente und den Balken aufgeteilt, die jeweils einzeln betrachtet werden. Dabei wird davon ausgegangen, dass an der Verbindungsfuge definierbare Schubkräfte T übertragen werden, wenn der Plattenbalken für die Berechnung als Gesamtquerschnitt betrachtet werden soll.

Die Scheibe wird als dünnes, ebenes Tragelement betrachtet, welches nur in seiner Ebene beansprucht wird. Biegebeanspruchungen und somit auch alle orthogonal zur Platte stehenden Spannungen werden vernachlässigt, demnach werden nur Spannungen in der Mittelebene der Platte betrachtet. Die in der Verbindungsfuge wirkenden Schubkräfte T bewirken Zugkräfte im Steg und Druckkräfte in den angrenzenden Platten. Infolge der Schubverzerrung der Platte werden die resultierenden Druckspannungen in der Platte mit zunehmenden Abstand vom Steg immer kleiner.

Eine genaue Ermittlung der Spannungsverteilung in der Platte kann mittels AIRY'scher Spannungsfunktion erfolgen, die über Randbedingungen gelöst werden kann. Ein Beispiel liefert hier Literatur von Hake ^[4]. Der Aufwand für die Berechnung ist jedoch groß und für die praktische Anwendung eher unhandlich.

Berechnung nach technischer Biegelehre

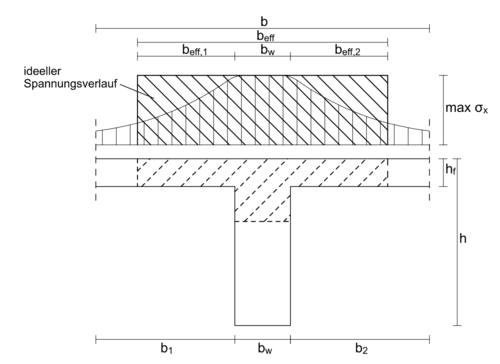
Realer und idealer Druckspannungsverlauf im Plattenbalken

Bei der Biegespannungsermittlung nach technischer Biegelehre wird zunächst eine konstante Spannungsverteilung über die gesamte Querschnittsbreite vorausgesetzt. Insbesondere bei stark gegliederten Querschnitten mit breiten Gurten ist diese Annahme aus den im vorhergehenden Abschnitt genannten Gründen nicht gerechtfertigt. Um bei Plattenbalken dennoch eine Berechnung nach technischer Biegelehre zu ermöglich (deutlich anwendungsfreundlicher als nach Scheibentheorie), wird ein Ersatzsystem definiert, bei dem die tatsächlichen durch das Mittragen der Platte entstehenden Längsdruckspannungen in einen idealisierten Spannungskörper umgelagert werden.

Dabei erfolgt die Definition der mitwirkenden Plattenbreite unter dem Grundsatz, dass die am idealisierten Spannungskörper auftretende Gesamtdruckkraft etwa die gleiche Größe hat, wie die Druckkraft unter den wirklich auftretenden Spannungen. Dies erfordert streng genommen eine Betrachtung des Volumenkörpers der auftretenden Spannungen σ_x. Häufig beschränken sich die Betrachtungen jedoch auf die Spannungen am gedrückten Rand (z. B. Leonhardt^[5]). In diesem Fall soll der Flächeninhalt des idealisierten Spannungsverlaufs dann etwa dem Flächeninhalt der real verlaufenden Spannungen entlang des oberen Randes entsprechen.

Als Bezugsgröße für den idealisierten Spannungsverlauf wird die max Druckspannung max σ_x verwendet. Da im Bereich der Stegbreite der Dehnungsverlauf ε_x konstant ist, beschränken sich die Gleichwertigkeitsbetrachtungen nur auf die abliegenden Plattenabschnitte (nach ^[5]):

b_{eff,1}\cdot {max}\ \sigma _{x}=\int _{0}^{b_{1}}\sigma _{x}\cdot {dy_{1}}

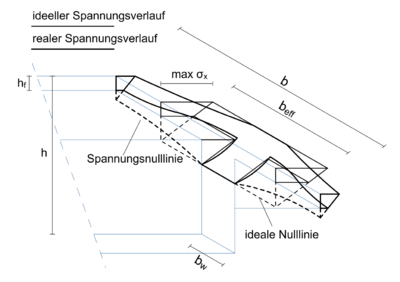
Aus der Idealisierung geht außerdem eine Veränderung der Spannungsnulllinie hervor. Im reellen Fall nähert sich diese mit steigendem Abstand zum Steg an die Platte an. Zur korrekten Anwendung der technischen Biegelehre hat die Spannung durch Benutzung der maßgebenden Höhe max σ_x an jeder Stelle denselben Abstand zur Nulllinie. Hierdurch verkleinert sich folglich der innere Hebelarm der Kräfte, was zu einer höheren Sicherheit der Näherungsmethode führt. ^[3]

Schub- und Biegesteifigkeit der Platte

Dass die sich vom Steg entfernenden Bereiche der Platte mit steigender Entfernung dem Mitwirken entziehen, hat seinen Ursprung in der Schub- und Biegesteifigkeit der Platte. Letztere bleibt oft in den Betrachtungen unbeachtet, was dazu führt, dass die Ergebnisse zu sehr auf der sicheren Seite liegen. Einen Ansatz bietet Brendel mit der Unterteilung von b_eff in die jeweiligen Anteile, die in der Platte durch Ansatz der Schubsteifigkeit (b_eff,s) bzw. der Biegesteifigkeit (b_eff,b) mitwirken. ^[3]

Schubsteifigkeit der Platte

Diese Betrachtungen beruhen allein auf dem Ansatz der Scheibenwirkung der schubfest mit dem Steg verbundenen Platte. Biegemomente und vertikale Schubkräfte werden hier vernachlässigt. Je dünner die Platte ist, um so größer ist der Anteil der Schubsteifigkeit an der mitwirkenden Plattenbreite. Daher werden in vielen Arbeiten ausschließlich diese Anteile betrachtet.

Der mittragende Anteil aus Schubkräften b_eff,s ergibt sich aus den an der Fuge übertragenen Spannungen, die jedoch mit dem Abstand zum Steg innerhalb der Platte aufgrund von Schubverzerrungen abnehmen. Zusätzlich entzieht sich die Platte umso mehr der Mitwirkung, umso größer das Verhältnis zwischen der Plattenbreite zur effektiven Spannweite ist. ^[6]

Biegesteifigkeit der Platte

Da sich durch die Spannungsübertragung an der Verbindungsfuge auch Biegemomente übertragen, wird in der Platte neben der Schubsteifigkeit auch ihre Biegesteifigkeit aktiviert. Der Einfluss der Biegesteifigkeit steigt proportional zu dem Verhältnis der Plattendicke zur Steghöhe. Nach Marguerre ^[7] darf b_eff,b bei Plattenbreiten bis zu einem Viertel der Stützweite über die gesamte Breite als wirkend angenommen werden. Für breitere Platten werden in ^[3] einfache Beiwerte zur Abschätzung der mitwirkenden Plattenbreite b_eff,b angegeben, welche von einer isotropen Platte ausgehen. Die übliche Bewehrungsführung der querspannenden Platte verursacht jedoch zumeist eine größere Biegesteifigkeit quer zur Stützweite, was zur Folge hat, dass der wirksame Bereich von b_eff,b in Wirklichkeit größer ist ^[3].

Kräfteverlauf

Kraftverlauf in der Platte und im Balken

Wie es die Abbildung zeigt, kann der Kräfteverlauf innerhalb von Plattenbalken mittels Zug- und Druckspannungstrajektorien dargestellt werden. ^[5] Bei verteilter Last nimmt die Mitwirkung der Platte bei zunehmender Beanspruchung zu. Je nach System und Bewehrungsmenge wird die maximal mögliche mitwirkende Breite kurz vor dem Versagen voll ausgenutzt. Die Gründe dafür sind zum einen die Werkstoffeigenschaften von Beton, der im Druckbereich bei hoher ständiger Beanspruchung nichtlineare Kriecherscheinungen aufweist, und zum anderen jene von Stahl, der nach Überschreiten der Fließgrenze stärkere Dehnungserscheinungen hat. Die Rissbildung und Plastizierung haben einen positiven Effekt auf die mitwirkende Plattenbreite, sodass die Berechnung nach dem Eurocode, welche auf ungerissenen Druckgurten beruht, auf der sicheren Seite liegt. ^[8]

Auflager

Einschnürung der mitwirkenden Plattenbreite am Auflager (oben) und bei Einzellasten (unten) (Darstellung nach Schleeh)^[9]

Im Auflagerbereich muss sich das Mitwirken der Platte zunächst einstellen, wie anhand der Druckspannungstrajektorien in vorheriger Abbildung zu erkennen ist. Die konkrete mitwirkende Plattenbreite b_eff ist also von der Entfernung zum Auflager abhängig.

Einzellasten

Auch bei Einzellasten und an Zwischenauflagern kommt es zu einer Verringerung der mitwirkenden Plattenbreite (Einschnürung). Diese nimmt demnach im Bereich von konzentrierten Einzellasten ab. Die Größe der Einschnürung ist nach Schleeh abhängig von dem Verhältnis der Plattenbreite zur Spannweite ( ${b}/{l_{eff}}$ ). Je kleiner das Verhältnis, desto geringer fällt die Einschnürung in Breite und Länge aus. Für bestimmte Systeme kommt es hier zu der Besonderheit, dass eine Einzellast in Feldmitte die Einschnürung aus den Auflagerungen abmindert. ^[9] Kritik gibt es hier jedoch von Chwalla hinsichtlich der konzentrierten Einzellasten aus der Theorie. Diese kommen so in der Praxis nicht vor. ^[10] Forschungsarbeiten von Brendel ergeben, dass sich die Einschnürung mit größeren Belastungen verkleinert. Eine Einzellast, die über mehr als ein Zehntel der effektiven Stützweite aufgeteilt ist, erzeugt außerdem auch keine signifikante Einschnürung mehr. ^[3]

Art des Systems

Je nach Art des Systems bildet sich die Mitwirkung innerhalb der Platte unterschiedlich aus. Zu unterscheiden sind Einzelträger, Durchlaufträger und Kragarme. Da sich die mitwirkende Plattenbreite nur zwischen den Momentennullpunkten entwickeln kann, bildet der Abstand der Momentennullpunkte l₀ eine wesentliche Einflussgröße. Auch macht es einen Unterschied, ob es sich um einen einfachen Plattenbalken mit ausgeprägert Plattenbreite oder eine Balkenreihe handelt.

Einfeldträger, Durchlaufträger, Kragarm

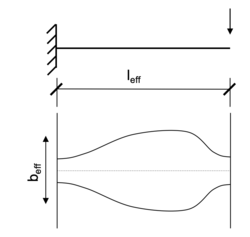
Prinzipieller Verlauf der mitwirkenden Plattenbreite am Kragarm (Darstellung nach Tulke)^[11]

Das jeweils vorliegende statische System ist maßgebend für den Abstand der Momentennullpunkte und daher bei der Ermittlung der mitwirkenden Plattenbreite zu berücksichtigen. Vereinfachte Angaben zur Ermittlung des Abstandes der Momentennullpunkte sind weiter oben auf dieser Seite angegeben ↑.

Die rechnerischen Beziehungen zur Ausbreitung der Druckspannungen in der Platte wurden auf Grundlage der Elastizitätstheorie für den ungerissenen Beton entwickelt und stellen daher für den Grenzzustand der Gebrauchstauglichkeit eine brauchbare Näherung dar. Im Grenzzustand der Tragfähigkeit nimmt die mitwirkende Plattenbreite wegen der Spannungsumlagerungen infolge Plastizierung mitunter deutlich zu. Die Berechnungsergebnisse auf der genannten Grundlage liegen damit auf der sicheren Seite.

Über Zwischenauflagern (Platte bildet den Zuggurt) ist wegen der Rissbildung des Betons nur eine eingeschränkte mitwirkende Plattenbreite zu erwarten. Um sicherzustellen, dass die Biegezugbewehrung dennoch über die gesamte Verteilungsbreite gleichmäßiog beansprucht wird, darf diese nach EC 2-1-1 im einseitigen Plattenabschnitt nur auf einer Breite von b_eff,i/2 ausgelagert werden.

Einfluss eines Endquerträgers

Kommt die Bauweise mit einem Endquerträger zum Einsatz, so entlastet dieser den Endquerrand der mitwirkenden Plattenbreite nur zu etwa 50%. Schleeh kommt bei seinen Untersuchungen zum Ergebnis, dass ein Endquerträger nur dann sinnvoll auszubilden wäre, wenn Spannungs-Dehnungs-Spitzen im Randbereich der Platte abgemindert werden müssen. Ein Randquerträger ist demnach erst ab einem Verhältnis von $l_{eff}\leq 4b_{i}$ sinnvoll, da bei einem größeren Verhältnis die Platte ohnehin in Gänze zur Mitwirkung hinzugezogen wird. ^[12]

Balkenreihe

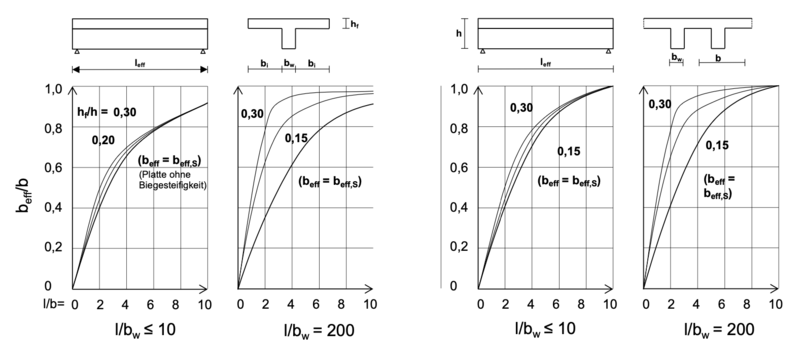
Die Abbildung zeigt jeweils für einen Einzelbalken und eine Balkenreihe die bezogene mitwirkende Plattenbreite in Balkenmitte, wobei die Diagramme jeweils für eine kleine sowie eine große effektive Stützweite erstellt wurden. Zusätzlich werden verschiedene Plattendicken berücksichtigt. Bei einer Aneinanderreihung von Plattenbalken in Querrichtung ist die Querverformung im Gegensatz zum Einzelbalken innerhalb der Platte durch das angrenzende System senkrecht zur Balkenstützweite behindert. Aus diesem Grund erhöht sich die mitwirkende Breite bei Balkenreihen im Gegensatz zu einzelnen Balken nach Brendel um bis zu 15%. Der Abbildung ist zusätzlich zu entnehmen, in welcher Hinsicht sich ein größeres Verhältnis der Plattendicke zur Gesamthöhe auf die Mitwirkung auswirkt (siehe auch ↑). Je dicker die Platte in diesem Verhältnis ist, desto größer ist der Einfluss der Biegesteifigkeit auf die gesamte mitwirkende Plattenbreite. Auffallend ist, dass vor allem bei großen Stützweiten die Dicke der Platte zu einem größeren mitwirkenden Effekt führt. ^[3]

Die bezogene mitwirkende Plattenbreite in Feldmitte für Einzelbalken (links) und Balkenreihen (rechts) (angelehnt an Brendel) ^[3]

Computerbasierte FE-Berechnung

Erste Ergebnisse zur Ermittlung der mitwirkenden Plattenbreite mit Hilfe der Finite-Elemente-Methode liefern z. B. Arbeiten von Loo & Sutandi ^[13] aus 1986, die mit dem Ziel durchgeführt wurde, empirische Formeln auf statistischer Grundlage bereitzustellen. Im Ergebnis dieser Arbeit wurden drei einfache und konkrete Berechnungsformeln für Plattenbalken unter Gleichlasten und Einzellasten bereitgestellt, die eine ganze Reihe von Einflussfaktoren auf die mitwirkende Plattenbreite berücksichtigen (Trägerspannweite, Trägerabstand, Stegdicke, Gesamtquerschnittshöhe, Plattendicke). Für gleichmäßig verteilte Lasten ergibt sich beispielsweise folgender Ansatz:

{\frac {b_{eff}}{b}}=0,8651\cdot \left({\frac {b}{l_{eff}}}\right)^{-0,1656}\cdot \left({\frac {h_{f}}{h}}\right)^{0,1370}\cdot \left({\frac {b_{w}}{h}}\right)^{-0,0312}\cdot \left({\frac {l_{eff}}{h}}\right)^{0,0191}

Bei einem Vergleich mit konventionellen Berechnungsformeln in 12 verschiedenen Normen und Regelwerken kommen die Autoren zu der Schlussfolgerung, dass die mitwirkende Plattenbreite unter gleichmäßig verteilter Belastung in den meisten Regelwerken zu konservativ ermittelt wird. Bei konzentrierter Belastung tendieren einige Normen in Fällen mit geringem Trägerabstand teilweise auf die unsichere Seite.
Eine andere Autoren haben auf die gleichen Versuchsergebnisse Bezug genommen und ähnliche Formeln entwickelt (z. B. Utku und Aygar ^[14]):

{\cfrac {b_{eff}}{b}}=0,9450-0,4630\cdot {\cfrac {b}{l_{eff}}}+0,0016\cdot {\cfrac {l_{eff}}{h}}+0,0222\cdot {\cfrac {b_{w}}{h}}+0,1810\cdot {\cfrac {h_{f}}{h}}

Für konkrete Berechnungsergebnisse mit Hilfe dieser Formel - siehe Mitwirkende Plattenbreite - Geschichtliche Entwicklung und normative Regeln.

Fazit

Die Näherungsformel für die mitwirkende Plattenbreite nach ^[1] soll auf möglichst einfache Art und Weise einen hinreichend genauen Wert für die mitwirkende Plattenbreite liefern und dabei die wesentlichen Einflussfaktoren berücksichtigen. Sie wurde im Laufe des letzten Jahrhunderts entwickelt und durch viele wissenschaftliche Arbeiten gestützt und verbessert. In vielen Ländern außerhalb des Eurocodes werden genau die gleichen oder ähnliche Ansätze zur Berechnung vorgeschlagen, einige davon sind wesentlich ungenauer als im Eurocode (siehe Mitwirkende Plattenbreite - Geschichtliche Entwicklung und normative Regeln).

Die Genauigkeit der Berechnung spielt in der Praxis keine sehr große Rolle, da sich der Hebelarm der inneren Kräfte und damit die erforderliche Bewehrung mit der Größe der mitwirkenden Breite kaum ändert und die Biegedruckzone bei Plattenbalken häufig nur mäßig ausgenutzt wird. Lediglich bei Sonderbauten oder Optimierungsaufgaben kann eine genauere Berechnung wirtschaftlichere Ergebnisse liefern und sinnvoll sein. ^[15]

Quellen

↑ ^1,0 ^1,1 DIN EN 1992-1-1 Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau mit Nationalem Anhang, Abschnitt 5.3.2.1, Beuth Verlag GmbH 2016
↑ Fingerloos, Frank: Der Eurocode 2 für Deutschland - Erläuterungen und Hintergründe. In: Beton- und Stahlbetonbau 105 (2010), Nr. 7, S. 406–420. – ISSN 00059900
↑ ^3,0 ^3,1 ^3,2 ^3,3 ^3,4 ^3,5 ^3,6 ^3,7 Brendel, G.: Die mitwirkende Plattenbreite nach Theorie und Versuch. In: Beton- und Stahlbetonbau 55 (1960), Nr. 8, S. 177–185. – ISSN 00059900
↑ Hake, Erwin ; Meskouris, Konstantin: Statik der Flächentragwerke: Einführung mit vielen durchgerechneten Beispielen. 2., korr. Aufl. Berlin : Springer, 2007 (Springer-Lehrbuch). – ISBN 978–3–540–72623–4
↑ ^5,0 ^5,1 ^5,2 Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6
↑ Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900
↑ Marguerre, K.: Über die Beanspruchung von Plattenträgern. Stahlbau (1952)
↑ Peil, U.: Mitwirkende Plattenbreite - Eine Richtigstellung. In: Beton- und Stahlbetonbau 74 (1979), Nr. 10, S. 243–246. – ISSN 00059900
↑ ^9,0 ^9,1 Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900
↑ Chwalla, E.: Die Formeln zur Berechnung der "voll mitwirkenden Breite" dünner Gurt- und Rippenplatten. In: Stahlbau (1936), Nr. 10, S. 73
↑ Tulke, J.: Berechnung monolithischer Decken-Balken-Systeme: Umsetzung in einer webbasierten Umgebung. Berlin, TU Berlin, Diplomarbeit, 2001
↑ Schleeh, W.: Die Bedeutung des Endquerträgers beim Plattenbalken. In: Beton- und Stahlbetonbau 72 (1977), Nr. 4, S. 85–91. – ISSN 00059900
↑ Loo, Y.-C ; Sutani ; T.D.: Effective flange width formulas for T-beams. In: Concrete International. Design and Construction 8 (1986), Nr. 2, S. 40–45
↑ Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)
↑ Grasser, E. ; Moosecker, W.: Hilfsmittel zur näherungsweisen Bestimmung der mitwirkenden Breite von Plattenbalken im Stahlbetonbau. In: Beton- und Stahlbetonbau 77 (1982), Nr. 6, S. 164–167. – ISSN 00059900

Seiteninfo

Status: Seite geprüft, inhaltlich OK

[EC_2-1-1-1] 1,0 ^1,1 DIN EN 1992-1-1 Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau mit Nationalem Anhang, Abschnitt 5.3.2.1, Beuth Verlag GmbH 2016

[2] Fingerloos, Frank: Der Eurocode 2 für Deutschland - Erläuterungen und Hintergründe. In: Beton- und Stahlbetonbau 105 (2010), Nr. 7, S. 406–420. – ISSN 00059900

[Brendel1960-3] 3,0 ^3,1 ^3,2 ^3,3 ^3,4 ^3,5 ^3,6 ^3,7 Brendel, G.: Die mitwirkende Plattenbreite nach Theorie und Versuch. In: Beton- und Stahlbetonbau 55 (1960), Nr. 8, S. 177–185. – ISSN 00059900

[4] Hake, Erwin ; Meskouris, Konstantin: Statik der Flächentragwerke: Einführung mit vielen durchgerechneten Beispielen. 2., korr. Aufl. Berlin : Springer, 2007 (Springer-Lehrbuch). – ISBN 978–3–540–72623–4

[Leonhardt-5] 5,0 ^5,1 ^5,2 Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6

[6] Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900

[7] Marguerre, K.: Über die Beanspruchung von Plattenträgern. Stahlbau (1952)

[Peil-8] Peil, U.: Mitwirkende Plattenbreite - Eine Richtigstellung. In: Beton- und Stahlbetonbau 74 (1979), Nr. 10, S. 243–246. – ISSN 00059900

[Schleeh1973-9] 9,0 ^9,1 Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900

[10] Chwalla, E.: Die Formeln zur Berechnung der "voll mitwirkenden Breite" dünner Gurt- und Rippenplatten. In: Stahlbau (1936), Nr. 10, S. 73

[11] Tulke, J.: Berechnung monolithischer Decken-Balken-Systeme: Umsetzung in einer webbasierten Umgebung. Berlin, TU Berlin, Diplomarbeit, 2001

[12] Schleeh, W.: Die Bedeutung des Endquerträgers beim Plattenbalken. In: Beton- und Stahlbetonbau 72 (1977), Nr. 4, S. 85–91. – ISSN 00059900

[13] Loo, Y.-C ; Sutani ; T.D.: Effective flange width formulas for T-beams. In: Concrete International. Design and Construction 8 (1986), Nr. 2, S. 40–45

[14] Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)

[15] Grasser, E. ; Moosecker, W.: Hilfsmittel zur näherungsweisen Bestimmung der mitwirkenden Breite von Plattenbalken im Stahlbetonbau. In: Beton- und Stahlbetonbau 77 (1982), Nr. 6, S. 164–167. – ISSN 00059900

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

@@ Zeile 1: / Zeile 1: @@
-[[Datei:Mitwirkende Plattenbreite 1.1.png|right|thumb|500px|Mitwirkende Plattenbreite - realer/ideeller Spannungsverlauf in der Platte]]
+[[Datei:Mitwirkende Plattenbreite11-1.gif|right|thumb|500px|Mitwirkende Plattenbreite - realer/ideeller Spannungsverlauf in der Platte]]
 <br />
@@ Zeile 23: / Zeile 23: @@
 </ul>
-Der Eurocode 2 enthält eine Näherungsformel für die mitwirkende Plattenbreite, die für den normalen Hochbau ausreichend genaue Ergebnisse liefert. Ausreichend genau bedeutet hier, dass das Ergebnis auf der sicheren Seite liegt und eine genaue Berechnung oft nicht wirtschaftlicher im Vergleich zur Nutzung der Näherungsformel wäre.
+Der Eurocode 2 <ref name = "EC 2-1-1"> DIN EN 1992-1-1 Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau mit Nationalem Anhang, Abschnitt 5.3.2.1, Beuth Verlag GmbH 2016 </ref> enthält eine Näherungsformel für die mitwirkende Plattenbreite, die für den normalen Hochbau ausreichend genaue Ergebnisse liefert. Ausreichend genau bedeutet hier, dass das Ergebnis auf der sicheren Seite liegt und eine genaue Berechnung oft nicht wirtschaftlicher im Vergleich zur Nutzung der Näherungsformel wäre.
 == Berechnungsgrundlagen==
@@ Zeile 38: / Zeile 38: @@
 === Berechnung nach Eurocode 2-1-1===
+[[Datei:Mitwirkende Plattenbreite 1.1.png|right|thumb|500px|Mitwirkende Plattenbreite - mit Bezeichnungen nach EC 2]]
 Für Nachweise im Grenzzustand der Tragfähigkeit und der Gebrauchstauglichkeit darf die mitwirkende Plattenbreite wie folgt ermittelt werden:
 :<math>b_{eff}=\sum b_{eff,i} + b_{w}\le b</math> <br />
@@ Zeile 75: / Zeile 76: @@
 [[Datei:Mitwirkende Plattenbreite 5.1.png|right|thumb|300px|Mitwirkung der Platte über eine Schubkraft T entlang der Verbindungsfuge (Darstellung nach ''Brendel'')<ref Name= "Brendel1960">Brendel, G.: Die mitwirkende Plattenbreite nach Theorie und Versuch. In: Beton- und Stahlbetonbau 55 (1960), Nr. 8, S. 177–185. – ISSN 00059900</ref>]]
-Die Scheibentheorie befasst sich mit der Berechnung von Spannungen und Verformungen innerhalb von Scheibenelementen. Nach der Theorie wird ein Plattenbalken in zwei Plattenelemente und den Balken aufgeteilt, die jeweils einzeln betrachtet werden. Dabei wird davon ausgegangen, dass an der Verbindungsfuge eine definierbare Schubkraft T übertragen wird, wenn der Plattenbalken für die Berechnung als Gesamtquerschnitt betrachtet werden soll. Die Scheibe wird als dünnes, ebenes Tragelement betrachtet, welches nur in seiner Ebene beansprucht wird. Biegebeanspruchungen und somit auch alle orthogonal zur Platte stehenden Spannungen werden vernachlässigt, demnach werden nur Spannungen in der Mittelebene der Platte betrachtet. Die genaue Berechnung der mitwirkenden Plattenbreite erfolgt mittels AIRY'scher Spannungsfunktion, die über Randbedingungen gelöst werden kann. Ein Beispiel liefert hier Literatur von <i>Hake</i> <ref>Hake, Erwin ; Meskouris, Konstantin: Statik der Flächentragwerke: Einführung mit vielen durchgerechneten Beispielen. 2., korr. Aufl. Berlin : Springer, 2007 (Springer-Lehrbuch). – ISBN 978–3–540–72623–4</ref>. Der Aufwand ist jedoch groß, sodass eine Berechnung nach technischer Biegelehre meist sinnvoller ist.
+Die Scheibentheorie befasst sich mit der Berechnung von Spannungen und Verformungen innerhalb von Scheibenelementen. Nach dieser Theorie wird ein Plattenbalken in zwei Plattenelemente und den Balken aufgeteilt, die jeweils einzeln betrachtet werden. Dabei wird davon ausgegangen, dass an der Verbindungsfuge definierbare Schubkräfte T übertragen werden, wenn der Plattenbalken für die Berechnung als Gesamtquerschnitt betrachtet werden soll.<br>
+Die Scheibe wird als dünnes, ebenes Tragelement betrachtet, welches nur in seiner Ebene beansprucht wird. Biegebeanspruchungen und somit auch alle orthogonal zur Platte stehenden Spannungen werden vernachlässigt, demnach werden nur Spannungen in der Mittelebene der Platte betrachtet.
+Die in der Verbindungsfuge wirkenden Schubkräfte T bewirken Zugkräfte im Steg und Druckkräfte in den angrenzenden Platten. Infolge der Schubverzerrung der Platte werden die resultierenden Druckspannungen in der Platte mit zunehmenden Abstand vom Steg immer kleiner.<br>
+Eine genaue Ermittlung der Spannungsverteilung in der Platte kann mittels AIRY'scher Spannungsfunktion erfolgen, die über Randbedingungen gelöst werden kann. Ein Beispiel liefert hier Literatur von <i>Hake</i> <ref>Hake, Erwin ; Meskouris, Konstantin: Statik der Flächentragwerke: Einführung mit vielen durchgerechneten Beispielen. 2., korr. Aufl. Berlin : Springer, 2007 (Springer-Lehrbuch). – ISBN 978–3–540–72623–4</ref>. Der Aufwand für die Berechnung ist jedoch groß und für die praktische Anwendung eher unhandlich.
 === Berechnung nach technischer Biegelehre===
 [[Datei:Mitwirkende Plattenbreite 2.1.png|right|thumb|400px|Realer und idealer Druckspannungsverlauf im Plattenbalken ]]
-Bei der Biegespannungsermittlung nach technischer Biegelehre wird eine konstante Spannungsverteilung über die Querschnittsbreite vorausgesetzt. Um diesen Zustand beim Plattenbalken zu erreichen, wird ein Ersatzsystem definiert, bei dem die tatsächlichen durch das Mittragen der Platte entstehenden Längsdruckspannungen in einen idealisierten Spannungskörper umgelagert werden.
+Bei der Biegespannungsermittlung nach technischer Biegelehre wird zunächst eine konstante Spannungsverteilung über die gesamte Querschnittsbreite vorausgesetzt. Insbesondere bei stark gegliederten Querschnitten mit breiten Gurten ist diese Annahme aus den im vorhergehenden Abschnitt genannten Gründen nicht gerechtfertigt. Um bei Plattenbalken dennoch eine Berechnung nach technischer Biegelehre zu ermöglich (deutlich anwendungsfreundlicher als nach Scheibentheorie), wird ein Ersatzsystem definiert, bei dem die tatsächlichen durch das Mittragen der Platte entstehenden Längsdruckspannungen in einen idealisierten Spannungskörper umgelagert werden.<br>
-Dabei erfolgt die Definition der mitwirkenden Plattenbreite unter dem Grundsatz, dass die am idealisierten Spannungskörper auftretende Gesamtdruckkraft etwa die gleiche Größe hat, wie die Druckkraft unter den wirklich auftretenden Spannungen. Dies erfordert streng genommen eine Betrachtung des Volumenkörpers der auftretenden Spannungen &sigma;<sub>x</sub>. Häufig beschränken sich die Betrachtungen jedoch auf die Spannungen am gedrückten Rand (z. B. ''Leonhardt''<ref Name = "Leonhardt"> Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6 </ref>). In diesem Fall soll der Flächeninhalt des idealisierten Spannungsverlaufs dann etwa dem Flächeninhalt der real verlaufenden Spannungen entlang des oberen Randes entsprechen.
+Dabei erfolgt die Definition der mitwirkenden Plattenbreite unter dem Grundsatz, dass die am idealisierten Spannungskörper auftretende Gesamtdruckkraft etwa die gleiche Größe hat, wie die Druckkraft unter den wirklich auftretenden Spannungen. Dies erfordert streng genommen eine Betrachtung des Volumenkörpers der auftretenden Spannungen &sigma;<sub>x</sub>. Häufig beschränken sich die Betrachtungen jedoch auf die Spannungen am gedrückten Rand (z. B. ''Leonhardt''<ref Name = "Leonhardt"> Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6 </ref>). In diesem Fall soll der Flächeninhalt des idealisierten Spannungsverlaufs dann etwa dem Flächeninhalt der real verlaufenden Spannungen entlang des oberen Randes entsprechen.<br>
 Als Bezugsgröße für den idealisierten Spannungsverlauf wird die max Druckspannung max &sigma;<sub>x</sub> verwendet. Da im Bereich der Stegbreite der Dehnungsverlauf &epsilon;<sub>x</sub> konstant ist, beschränken sich die Gleichwertigkeitsbetrachtungen nur auf die abliegenden Plattenabschnitte (nach <ref Name = "Leonhardt"/>):
-:<math>b_{eff,1} \cdot {max} \:\sigma_x = \int_0^{b_1} \sigma_x \: {dy_1} </math> <br />
+:<math>b_{eff,1} \cdot {max}\ \sigma_x = \int_0^{b_1} \sigma_x \cdot {dy_1} </math> <br />
-Der Flächeninhalt der realen Spannungen soll demnach dem der idealisierten Spannungen mit der vorgegebenen Höhe max &sigma;<sub>x</sub> entsprechen. Aus der Idealisierung geht eine Veränderung der Spannungsnulllinie hervor. Im reellen Fall nähert sich diese mit steigendem Abstand zum Steg an die Platte an. Zur korrekten Anwendung der technischen Biegelehre hat die Spannung durch Benutzung der maßgebenden Höhe max &sigma;<sub>x</sub> an jeder Stelle denselben Abstand zur Nulllinie. Hierdurch verkleinert sich folglich der innere Hebelarm der Kräfte, was zu einer höheren Sicherheit der Näherungsmethode führt. <ref name = "Brendel1960"/>
+Aus der Idealisierung geht außerdem eine Veränderung der Spannungsnulllinie hervor. Im reellen Fall nähert sich diese mit steigendem Abstand zum Steg an die Platte an. Zur korrekten Anwendung der technischen Biegelehre hat die Spannung durch Benutzung der maßgebenden Höhe max &sigma;<sub>x</sub> an jeder Stelle denselben Abstand zur Nulllinie. Hierdurch verkleinert sich folglich der innere Hebelarm der Kräfte, was zu einer höheren Sicherheit der Näherungsmethode führt. <ref name = "Brendel1960"/>
 === Schub- und Biegesteifigkeit der Platte===
-Dass die sich vom Steg entfernenden Bereiche der Platte mit steigender Entfernung dem Mitwirken entziehen, hat seinen Ursprung in der Schub- und Biegesteifigkeit der Platte. Letztere bleibt oft in den Betrachtungen unbeachtet, was dazu führt, dass die Ergebnisse zu sehr auf der sicheren Seite liegen. Einen Ansatz bietet <i>Brendel</i> mit der Unterteilung von b<sub>eff</sub> in die jeweiligen Anteile, die in der Platte durch Schubfestigkeit (b<sub>eff,s</sub>) und durch die Biegesteifigkeit (b<sub>eff,b</sub>) mitwirken. <ref name = "Brendel1960"/>
+Dass die sich vom Steg entfernenden Bereiche der Platte mit steigender Entfernung dem Mitwirken entziehen, hat seinen Ursprung in der Schub- und Biegesteifigkeit der Platte. Letztere bleibt oft in den Betrachtungen unbeachtet, was dazu führt, dass die Ergebnisse zu sehr auf der sicheren Seite liegen. Einen Ansatz bietet <i>Brendel</i> mit der Unterteilung von b<sub>eff</sub> in die jeweiligen Anteile, die in der Platte durch Ansatz der Schubsteifigkeit (b<sub>eff,s</sub>) bzw. der Biegesteifigkeit (b<sub>eff,b</sub>) mitwirken. <ref name = "Brendel1960"/>
-==== Schubsicherer Verbund====
+====Schubsteifigkeit der Platte====
-Eine schubsichere Verbindung zwischen der Platte und dem Balken wird heute mittels Bügeln und ausreichender Bewehrung gewährleistet. Dabei wird der Schubübertrag als so groß angenommen, dass der Plattenbalken als monolithisch angesehen werden darf. Durch diese Verbindung erfahren beide Bauteile an der Anschlussstelle bei Biegung dieselben Längsdehnungen. Während der Belastung auf Biegung kommt es im Zustand II, also bei der Überschreitung der Betonzugfestigkeit innerhalb der Biegezugzone, zu Betondruckstreben zwischen den Rissen und zu Zugstreben der Anschlussbewehrung. Begleiterscheinung von Biegung ist immer eine Längsschubkraft &tau;. Diese wirkt in horizontaler Richtung in der Verbindungsfuge zwischen Platte und Balken und wurde bereits mit T definiert. Diese Schubkraft beansprucht die Platte vereinfacht als Scheibe, vertikale Schubkräfte werden hier vernachlässigt. <ref name = "Leonhardt"/> <br />
+Diese Betrachtungen beruhen allein auf dem Ansatz der Scheibenwirkung der schubfest mit dem Steg verbundenen Platte. Biegemomente und vertikale Schubkräfte werden hier vernachlässigt. Je dünner die Platte ist, um so größer ist der Anteil der Schubsteifigkeit an der mitwirkenden Plattenbreite. Daher werden in vielen Arbeiten ausschließlich diese Anteile betrachtet. <br>
-Bei kompakten Querschnitten ist der Einfluss der Schubkräfte verschwindend gering, je filigraner die Querschnitte, desto präsenter sind sie. Der mittragende Anteil aus Schubkräften b<sub>eff,s</sub> ergibt sich aus den an der Fuge übertragenden Spannungen, die jedoch mit dem Abstand zum Steg innerhalb der Platte aufgrund von Schubverzerrungen abnehmen. Zusätzlich entzieht sich die Platte umso mehr der Mitwirkung, umso größer das Verhältnis zwischen der Plattenbreite zur effektiven Spannweite ist. <ref>Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900</ref>
+Der mittragende Anteil aus Schubkräften b<sub>eff,s</sub> ergibt sich aus den an der Fuge übertragenen Spannungen, die jedoch mit dem Abstand zum Steg innerhalb der Platte aufgrund von Schubverzerrungen abnehmen. Zusätzlich entzieht sich die Platte umso mehr der Mitwirkung, umso größer das Verhältnis zwischen der Plattenbreite zur effektiven Spannweite ist. <ref>Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900</ref>
 ==== Biegesteifigkeit der Platte====
-Da sich durch die Spannungsübertragung an der Verbindungsfuge auch Biegemomente übertragen, wird die Platte neben der Schubsteifigkeit auch auf seine Biege- steifigkeit beansprucht. Die Größe vom Biegemoment steigt proportional zu dem Verhältnis der Plattendicke zur Steghöhe. Nach <i>Marguerre</i> <ref>Marguerre, K.: Über die Beanspruchung von Plattenträgern. Stahlbau (1952) </ref> darf b<sub>eff,b</sub> bei Plattenbreiten bis zu einem Viertel der Stützweite über die gesamte Breite als wirkend angenommen werden. Die Bewehrungsführung verursacht zumeist eine größere Biegesteifigkeit quer zur Stützweite, was zur Folge hat, dass der wirksame Bereich von b<sub>eff,b</sub> in Wirklichkeit größer ist. Ein größeres Verhältnis von Stützweite zu Stegbreite führt dazu, dass sich das Trägheitsmoment stärker auf den Gesamtquerschnitt auswirkt. b<sub>eff,b</sub> ist demnach vor allem bei gedrungeneren Stegen Beachtung zu schenken. <ref name = "Brendel1960" />
+Da sich durch die Spannungsübertragung an der Verbindungsfuge auch Biegemomente übertragen, wird in der Platte neben der Schubsteifigkeit auch ihre Biegesteifigkeit aktiviert. Der Einfluss der Biegesteifigkeit steigt proportional zu dem Verhältnis der Plattendicke zur Steghöhe. Nach <i>Marguerre</i> <ref>Marguerre, K.: Über die Beanspruchung von Plattenträgern. Stahlbau (1952) </ref> darf b<sub>eff,b</sub> bei Plattenbreiten bis zu einem Viertel der Stützweite über die gesamte Breite als wirkend angenommen werden. Für breitere Platten werden in <ref name = "Brendel1960" /> einfache Beiwerte zur Abschätzung der mitwirkenden Plattenbreite b<sub>eff,b</sub> angegeben, welche von einer isotropen Platte ausgehen. Die übliche Bewehrungsführung der querspannenden Platte verursacht jedoch zumeist eine größere Biegesteifigkeit quer zur Stützweite, was zur Folge hat, dass der wirksame Bereich von b<sub>eff,b</sub> in Wirklichkeit größer ist <ref name = "Brendel1960" />.
 === Kräfteverlauf===
@@ Zeile 106: / Zeile 111: @@
 [[File:Mitwirkende Plattenbreite 6.png|thumb|right|250px|Kraftverlauf in der Platte und im Balken]]
-Wie es die Abbildung zeigt, kann der Kräfteverlauf innerhalb von Plattenbalken mittels Zug- und Druckspannungstrajektorien dargestellt werden. <ref name="Leonhardt" /> Bei verteilter Last nimmt die Mitwirkung der Platte bei zunehmender Beanspruchung zu. Je nach System und Bewehrungsmenge wird die maximal mögliche mitwirkende Breite kurz vor dem Versagen voll ausgenutzt. Die Gründe dafür sind zum einen die Werkstoffeigenschaften von Beton, der im Druckbereich bei ständiger Beanspruchung nichtlineare Kriecherscheinungen aufweist, und zum anderen jene von Stahl, der nach Überschreiten der Fließgrenze stärkere Dehnungserscheinungen hat. Die Rissbildung und Plastizierung haben einen positiven Effekt auf die mitwirkende Plattenbreite, sodass die Berechnung nach dem Eurocode, der nur für ungerissene Druckgurte gilt, auf der sicheren Seite liegt. <ref Name="Peil">Peil, U.: Mitwirkende Plattenbreite - Eine Richtigstellung. In: Beton- und Stahlbetonbau 74 (1979), Nr. 10, S. 243–246. – ISSN 00059900</ref>
+Wie es die Abbildung zeigt, kann der Kräfteverlauf innerhalb von Plattenbalken mittels Zug- und Druckspannungstrajektorien dargestellt werden. <ref name="Leonhardt" /> Bei verteilter Last nimmt die Mitwirkung der Platte bei zunehmender Beanspruchung zu. Je nach System und Bewehrungsmenge wird die maximal mögliche mitwirkende Breite kurz vor dem Versagen voll ausgenutzt. Die Gründe dafür sind zum einen die Werkstoffeigenschaften von Beton, der im Druckbereich bei hoher ständiger Beanspruchung nichtlineare Kriecherscheinungen aufweist, und zum anderen jene von Stahl, der nach Überschreiten der Fließgrenze stärkere Dehnungserscheinungen hat. Die Rissbildung und Plastizierung haben einen positiven Effekt auf die mitwirkende Plattenbreite, sodass die Berechnung nach dem Eurocode, welche auf ungerissenen Druckgurten beruht, auf der sicheren Seite liegt. <ref Name="Peil">Peil, U.: Mitwirkende Plattenbreite - Eine Richtigstellung. In: Beton- und Stahlbetonbau 74 (1979), Nr. 10, S. 243–246. – ISSN 00059900</ref>
 ==== Auflager====
 [[Datei:Mitwirkende Plattenbreite 7.1.png|right|thumb|250px|Einschnürung der mitwirkenden Plattenbreite am Auflager (oben) und bei Einzellasten (unten) (Darstellung nach ''Schleeh'')<ref Name= "Schleeh1973"> Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900 </ref>]]
-Bei allen vorherigen Betrachtungen wird von frei aufliegenden Auflagern ausgegangen. Im Auflagerbereich muss sich das Mitwirken der Platte zunächst einstellen, wie in vorheriger Abbildung zu erkennen ist. Dies wird auch als Einschnürung bezeichnet, also eine Spannung, die sich aufgrund von Schubverzerrungen und Materialeigenschaften zunächst entwickeln muss. Grund dafür ist auch der Spannungsverlauf, der durch die Biegesteifigkeit der Platte entsteht.
+Im Auflagerbereich muss sich das Mitwirken der Platte zunächst einstellen, wie anhand der Druckspannungstrajektorien in vorheriger Abbildung zu erkennen ist. Die konkrete mitwirkende Plattenbreite b<sub>eff</sub> ist also von der Entfernung zum Auflager abhängig.
 ==== Einzellasten====
-Auch bei Einzellasten kommt es zu einer Einschnürung der mitwirkenden Plattenbreite. Diese nimmt demnach im Bereich von konzentrierten Einzellasten ab. Die Größe der Einschnürung ist nach <i>Schleeh</i> abhängig von dem Verhältnis der Plattenbreite zur Spannweite (<math>{b}/{l_{eff}}</math>). Je kleiner das Verhältnis, desto geringer fällt die Einschnürung in Breite und Länge aus. Für bestimmte Systeme kommt es hier zu der Besonderheit, dass eine Einzellast in Feldmitte die Einschnürung aus den Auflagerungen abmindert. <ref name = "Schleeh1973" /> Kritik gibt es hier jedoch von <i>Chwalla</i> hinsichtlich der konzentrierten Einzellasten aus der Theorie. Diese kommen so in der Praxis nicht vor. <ref>Chwalla, E.: Die Formeln zur Berechnung der "voll mitwirkenden Breite" dünner Gurt- und Rippenplatten. In: Stahlbau (1936), Nr. 10, S. 73</ref> Forschungsarbeiten von <i>Brendel</i> ergeben, dass sich die Einschnürung mit größeren Belastungen verkleinert. Eine Einzellast, die über mehr als ein Zehntel der effektiven Stützweite aufgeteilt ist, erzeugt außerdem auch keine signifikante Einschnürung mehr. <ref name = "Brendel1960" />
+Auch bei Einzellasten und an Zwischenauflagern kommt es zu einer Verringerung der mitwirkenden Plattenbreite (Einschnürung). Diese nimmt demnach im Bereich von konzentrierten Einzellasten ab. Die Größe der Einschnürung ist nach <i>Schleeh</i> abhängig von dem Verhältnis der Plattenbreite zur Spannweite (<math>{b}/{l_{eff}}</math>). Je kleiner das Verhältnis, desto geringer fällt die Einschnürung in Breite und Länge aus. Für bestimmte Systeme kommt es hier zu der Besonderheit, dass eine Einzellast in Feldmitte die Einschnürung aus den Auflagerungen abmindert. <ref name = "Schleeh1973" /> Kritik gibt es hier jedoch von <i>Chwalla</i> hinsichtlich der konzentrierten Einzellasten aus der Theorie. Diese kommen so in der Praxis nicht vor. <ref>Chwalla, E.: Die Formeln zur Berechnung der "voll mitwirkenden Breite" dünner Gurt- und Rippenplatten. In: Stahlbau (1936), Nr. 10, S. 73</ref> Forschungsarbeiten von <i>Brendel</i> ergeben, dass sich die Einschnürung mit größeren Belastungen verkleinert. Eine Einzellast, die über mehr als ein Zehntel der effektiven Stützweite aufgeteilt ist, erzeugt außerdem auch keine signifikante Einschnürung mehr. <ref name = "Brendel1960" />
 === Art des Systems===
-Je nach Art des Systems bildet sich die Mitwirkung innerhalb der Platte unterschiedlich aus. Zu unterscheiden sind Einzelträger, Durchlaufträger und Kragarme. Nach dem Eurocode gehen diese anhand der Momentennulldurchgänge über den Faktor l<sub>0</sub> in die Berechnung der mitwirkenden Plattenbreite mit ein. Auch macht es einen Unterschied, ob es sich um einen einfachen Plattenbalken oder eine Balkenreihe handelt.
+Je nach Art des Systems bildet sich die Mitwirkung innerhalb der Platte unterschiedlich aus. Zu unterscheiden sind Einzelträger, Durchlaufträger und Kragarme. Da sich die mitwirkende Plattenbreite nur zwischen den Momentennullpunkten entwickeln kann, bildet der Abstand der Momentennullpunkte l<sub>0</sub> eine wesentliche Einflussgröße. Auch macht es einen Unterschied, ob es sich um einen einfachen Plattenbalken mit ausgeprägert Plattenbreite oder eine Balkenreihe handelt.
-==== Einfeldträger====
-Der Einfeldträger ist aufgrund der einfachen Herstellungsvariante das meistgenutzte System, sodass die Wirkungsweise und der Kraftverlauf (siehe oben) umfassend erforscht sind.
-==== Kragarm====
+==== Einfeldträger, Durchlaufträger, Kragarm====
 [[Datei:Mitwirkende Plattenbreite 8.png|right|thumb|250px|Prinzipieller Verlauf der mitwirkenden Plattenbreite am Kragarm (Darstellung nach ''Tulke'')<ref>Tulke, J.: Berechnung monolithischer Decken-Balken-Systeme: Umsetzung in einer webbasierten Umgebung. Berlin, TU Berlin, Diplomarbeit, 2001 </ref>]]
+Das jeweils vorliegende statische System ist maßgebend für den Abstand der Momentennullpunkte und daher bei der Ermittlung der mitwirkenden Plattenbreite zu berücksichtigen. Vereinfachte Angaben zur Ermittlung des Abstandes der Momentennullpunkte sind weiter oben auf dieser Seite angegeben [[#Berechnung nach Eurocode 2-1-1|↑]]. <br>
-Die Regelungen für den Kragarm nach Eurocode <math>l_0 = 0,15 \cdot l_2 + l_3</math> unterscheiden sich nach analytischen Ergebnissen bei sehr kurzen Kragarmen stark vom realen Zustand, weshalb die Regelung mit <math>l_0 = 1,5 \cdot l_{eff,3}</math> erweitert wird, wobei der kleinere beider Werte maßgebend ist. Wie bei einer Einzellast oder im Auflagerbereich muss sich die Mitwirkung der Platte zunächst einmal einstellen.
+Die rechnerischen Beziehungen zur Ausbreitung der Druckspannungen in der Platte wurden auf Grundlage der Elastizitätstheorie für den ungerissenen Beton entwickelt und stellen daher für den Grenzzustand der Gebrauchstauglichkeit eine brauchbare Näherung dar. Im Grenzzustand der Tragfähigkeit nimmt die mitwirkende Plattenbreite wegen der Spannungsumlagerungen infolge Plastizierung mitunter deutlich zu. Die Berechnungsergebnisse auf der genannten Grundlage liegen damit auf der sicheren Seite. <br>
-==== Durchlaufträger====
+Über Zwischenauflagern (Platte bildet den Zuggurt) ist wegen der Rissbildung des Betons nur eine eingeschränkte mitwirkende Plattenbreite zu erwarten. Um sicherzustellen, dass die Biegezugbewehrung dennoch über die gesamte Verteilungsbreite gleichmäßiog beansprucht wird, darf diese nach EC 2-1-1 im einseitigen Plattenabschnitt nur auf einer Breite von b<sub>eff,i</sub>/2 ausgelagert werden.
-[[Datei:Mitwirkende Plattenbreite 9.1.png|right|thumb|250px|Prinzipieller Verlauf der mitwirkenden Plattenbreite bei Durchlaufträgern]]
-Über den Zwischenauflagern von Durchlaufträgern ist der obere Bereich des Plattenbalkens auf Zug beansprucht, der üblicherweise über die umgelagerte Zugbewehrung aufgenommen wird. Im Eurocode wird dieser Bereich mit der Lage der Momentennulldurchgänge berücksichtigt, wobei <math>l_0 = 0, 85 \cdot l_1</math> für Randfelder und <math>l_0 = 0,7 \cdot l_2</math> für Mittelfelder gilt. <br />
-Aufgrund der Werkstoffeigenschaften von Beton gelten für den ungerissenen Zustand der Biegezugzone dieselben Gesetzmäßigkeiten wie in der Druckzone. Im Zustand I wirkt der Beton somit auch im Zugbereich mit. <ref> Zilch, K.; Zehetmaier, G.: Bemessung im konstruktiven Betonbau (2010) </ref>
 ====Einfluss eines Endquerträgers====
@@ Zeile 141: / Zeile 136: @@
 ==== Balkenreihe====
-Die Abbildung zeigt jeweils für einen Einzelbalken und eine Balkenreihe die bezogene mitwirkende Plattenbreite in Balkenmitte, wobei die Diagramme jeweils eine kleine sowie eine große effektive Stützweite darstellen. Zusätzlich werden verschiedene Plattendicken berücksichtigt. Bei einer Aneinanderreihung von Plattenbalken in Querrichtung ist die Querverformung im Gegensatz zum Einzelbalken innerhalb der Platte durch das angrenzende System senkrecht zur Balkenstützweite behindert. Aus diesem Grund erhöht sich die mitwirkende Breite bei Balkenreihen im Gegensatz zu einzelnen Balken nach <i>Brendel</i> um bis zu 15%.  Der Abbildung ist zusätzlich zu entnehmen, in welcher Hinsicht sich ein größeres Verhältnis der Plattendicke zur Gesamthöhe auf die Mitwirkung auswirkt. Je dicker die Platte in diesem Verhältnis ist, desto größer ist der Einfluss der Biegesteifigkeit auf das Gesamtsystem. Hier wird mit   die Stützweite und die Plattendicke variiert. Auffallend ist, dass vor allem bei großen Stützweiten die Dicke der Platte zu einem größeren mitwirkenden Effekt führt.
+Die Abbildung zeigt jeweils für einen Einzelbalken und eine Balkenreihe die bezogene mitwirkende Plattenbreite in Balkenmitte, wobei die Diagramme jeweils für eine kleine sowie eine große effektive Stützweite erstellt wurden. Zusätzlich werden verschiedene Plattendicken berücksichtigt. Bei einer Aneinanderreihung von Plattenbalken in Querrichtung ist die Querverformung im Gegensatz zum Einzelbalken innerhalb der Platte durch das angrenzende System senkrecht zur Balkenstützweite behindert. Aus diesem Grund erhöht sich die mitwirkende Breite bei Balkenreihen im Gegensatz zu einzelnen Balken nach <i>Brendel</i> um bis zu 15%.  Der Abbildung ist zusätzlich zu entnehmen, in welcher Hinsicht sich ein größeres Verhältnis der Plattendicke zur Gesamthöhe auf die Mitwirkung auswirkt (siehe auch [[#Biegesteifigkeit der Platte|↑]]). Je dicker die Platte in diesem Verhältnis ist, desto größer ist der Einfluss der Biegesteifigkeit auf die gesamte mitwirkende Plattenbreite. Auffallend ist, dass vor allem bei großen Stützweiten die Dicke der Platte zu einem größeren mitwirkenden Effekt führt.
 <ref name= "Brendel1960" /> <br />
@@ Zeile 148: / Zeile 143: @@
 == Computerbasierte FE-Berechnung==
-Die computerbasierte Finite-Elemente-Methode ermöglicht es, Tragwerke computergestützt zu analysieren, die vorher einer Berechnung nicht zugänglich waren. Erste Ergebnisse liefern Arbeiten von <i>Loo & Sutandi</i> aus 1986, die feststellten, dass sich alle Normen weiterentwickelten, nur die Annahme zur mitwirkenden Plattenbreite hätte sich seit 34 Jahren nicht geändert, obwohl die Berechnungsmethoden in der Zeit sehr verfeinert wurden. Für die Methode wird der Plattenbalken in kleine (finite) Elemente unterteilt - die linearen 8-Knoten-Elemente, wobei jeder Knoten 3 Freiheitsgrade erhält. In alle Knoten werden sechs Kraftkomponenten, drei Normalkräfte und drei Querkräfte, eingerechnet. Über diese Methode erhielt zum ersten Mal die Plattendicke einen Einfluss auf die mitwirkende Plattenbreite. <ref> Loo, Y.-C ; Sutani ; T.D.: Effective flange width formulas for T-beams. In: Concrete International. Design and Construction 8 (1986), Nr. 2, S. 40–45 </ref> <br />
+Erste Ergebnisse zur Ermittlung der mitwirkenden Plattenbreite mit Hilfe der Finite-Elemente-Methode liefern z. B. Arbeiten von <i>Loo & Sutandi</i> <ref> Loo, Y.-C ; Sutani ; T.D.: Effective flange width formulas for T-beams. In: Concrete International. Design and Construction 8 (1986), Nr. 2, S. 40–45 </ref> aus 1986, die mit dem Ziel durchgeführt wurde, empirische Formeln auf statistischer Grundlage bereitzustellen. Im Ergebnis dieser Arbeit wurden drei einfache und konkrete Berechnungsformeln für Plattenbalken unter Gleichlasten und Einzellasten bereitgestellt, die eine ganze Reihe von Einflussfaktoren auf die mitwirkende Plattenbreite berücksichtigen (Trägerspannweite, Trägerabstand, Stegdicke, Gesamtquerschnittshöhe, Plattendicke). Für gleichmäßig verteilte Lasten ergibt sich beispielsweise folgender Ansatz:
-<i>Utku und Aygar</i> haben eine FE-Berechnung für einen Plattenbalken mit dem Computerprogramm <i>SAP2000</i> durchgeführt. Der Plattenbalken kann aufgrund seiner Symmetrie geviertelt werden. Das Viertel wird in 400 Quader mit jeweils 8 Knoten (lineare 8-Knoten-Elemente) aufgeteilt, wobei die Unterteilung innerhalb der Platte filigraner gewählt wird, da hier die Ergebnisse von größerer Bedeutung sind. Für jeden Knoten werden die Lagerbedingungen sowie der E-Modul vom Beton und die Querkontraktionszahl definiert. Bei Belastung mit einer konstanten Streckenlast lässt sich für verschiedene Abmessungen mittels Regressionsanalyse eine bezogene mitwirkende Plattenbreite in Abhängigkeit der Verhältnisse <math>\cfrac{b}{l_{eff}}</math>, <math>\cfrac{l_{eff}}{h}</math>, <math>\cfrac{b_w}{h}</math>  und <math>\cfrac{h_f}{h}</math> bestimmen.<ref>Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)</ref> <br/>
+: <math> \frac{ b_{ eff } }{ b }=0,8651 \cdot \left( \frac{ b }{ l_{ eff } } \right)^{ -0,1656 } \cdot \left( \frac{ h_{ f } }{ h } \right)^{ 0,1370 } \cdot \left( \frac{ b_{ w } }{ h } \right)^{ -0,0312 } \cdot \left( \frac{ l_{ eff } }{ h } \right)^{ 0,0191 } </math>
-<math>\cfrac{b_{eff}}{b} = 0,9450 - 0,4630 \cdot \cfrac{b}{l_{eff}} + 0,0016 \cdot \cfrac{l_{eff}}{h} + 0,0222 \cdot \cfrac{b_w}{h} + 0,1810 \cdot \cfrac{h_f}{h}</math>
+Bei einem Vergleich mit konventionellen Berechnungsformeln in 12 verschiedenen Normen und Regelwerken kommen die Autoren zu der Schlussfolgerung, dass die mitwirkende Plattenbreite unter gleichmäßig verteilter Belastung in den meisten Regelwerken zu konservativ ermittelt wird. Bei konzentrierter Belastung tendieren einige Normen in Fällen mit geringem Trägerabstand teilweise auf die unsichere Seite.<br>
+Eine andere Autoren haben auf die gleichen Versuchsergebnisse Bezug genommen und ähnliche Formeln entwickelt (z. B. <i>Utku und Aygar</i> <ref>Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)</ref>):
+:<math>\cfrac{b_{eff}}{b} = 0,9450 - 0,4630 \cdot \cfrac{b}{l_{eff}} + 0,0016 \cdot \cfrac{l_{eff}}{h} + 0,0222 \cdot \cfrac{b_w}{h} + 0,1810 \cdot \cfrac{h_f}{h}</math>
 </br>
 Für konkrete Berechnungsergebnisse mit Hilfe dieser Formel - siehe [[Mitwirkende Plattenbreite - Geschichtliche Entwicklung und normative Regeln]].
-<br />
-Auch in aktueller Literatur wird darauf verwiesen, dass es sich beim Plattenbalken um ein ausgesprochen komplexes, dreidimensionales Problem handelt. <i>Hartmann und Katz </i> verweisen darauf, dass es sich auch bei der Berechnung mit finiten Elementen um eine Näherungsmethode handelt, die noch zu aufwendig ist. Außerdem hat die exakte Ermittlung der Spannungen für die Bewehrungswahl kaum einen Einfluss.  Mögliche Modellansätze für Plattenbalken sind folgende:
-<ul>
-* Faltwerkmodelle
-** Platte und Balken  als Faltwerk (Schalenmodell)
-** Platte als Faltwerk, Unterzug als exzentrischer Balken oder Platte
-* Plattenmodelle
-** Platte als Platte und Unterzug als exzentrischer Balken
-** Platte mit zentrischem Balken
-</ul>
-Für den Vergleich der Ansätze wird hier auf weiterführende Literatur verwiesen. <ref Name="Hartmann"> Hartmann, F.; & Katz, C.:  Statik Mit Finiten Elementen (2. Aufl.), Springer (2019), S. 313-320</ref>
 == Fazit==
-Die Annäherungsformel für die mitwirkende Plattenbreite soll auf möglichst einfache Art und Weise möglichst viel Faktoren berücksichtigen. Sie wurde im Laufe des letzten Jahrhunderts entwickelt und durch viele wissenschaftliche Arbeiten verbessert. In vielen Ländern außerhalb des Eurocodes werden genau dieselben oder ähnliche Ansätze zur Berechnung vorgeschlagen, einige davon wesentlich ungenauer als im Eurocode. (siehe [[Mitwirkende Plattenbreite - Vergleichsrechnung]]) </br>
+Die Näherungsformel für die mitwirkende Plattenbreite nach <ref name = "EC 2-1-1"/> soll auf möglichst einfache Art und Weise einen hinreichend genauen Wert für die mitwirkende Plattenbreite liefern und dabei die wesentlichen Einflussfaktoren berücksichtigen. Sie wurde im Laufe des letzten Jahrhunderts entwickelt und durch viele wissenschaftliche Arbeiten gestützt und verbessert. In vielen Ländern außerhalb des Eurocodes werden genau die gleichen oder ähnliche Ansätze zur Berechnung vorgeschlagen, einige davon sind wesentlich ungenauer als im Eurocode (siehe [[Mitwirkende Plattenbreite - Geschichtliche Entwicklung und normative Regeln]]). </br>
-Die Genauigkeit der Berechnung spielt zudem keine sehr große Rolle, da sich der Hebelarm der inneren Kräfte und damit die erforderliche Bewehrung mit der Größe der mitwirkenden Breite kaum ändert und die Biegedruckzone bei Plattenbalken fast nie ausgenutzt wird. Lediglich bei Sonderbauten oder Optimierungsaufgaben kann eine genauere Berechnung wirtschaftlichere Ergebnisse liefern. <ref>Grasser, E. ; Moosecker, W.: Hilfsmittel zur näherungsweisen Bestimmung der mitwirkenden Breite von Plattenbalken im Stahlbetonbau. In: Beton- und Stahlbetonbau 77 (1982), Nr. 6, S. 164–167. – ISSN 00059900 </ref>
+Die Genauigkeit der Berechnung spielt in der Praxis keine sehr große Rolle, da sich der Hebelarm der inneren Kräfte und damit die erforderliche Bewehrung mit der Größe der mitwirkenden Breite kaum ändert und die Biegedruckzone bei Plattenbalken häufig nur mäßig ausgenutzt wird. Lediglich bei Sonderbauten oder Optimierungsaufgaben kann eine genauere Berechnung wirtschaftlichere Ergebnisse liefern und sinnvoll sein. <ref>Grasser, E. ; Moosecker, W.: Hilfsmittel zur näherungsweisen Bestimmung der mitwirkenden Breite von Plattenbalken im Stahlbetonbau. In: Beton- und Stahlbetonbau 77 (1982), Nr. 6, S. 164–167. – ISSN 00059900 </ref>
 ==Quellen==
@@ Zeile 175: / Zeile 161: @@
 {{Seiteninfo
-|Quality-flag = [[File:quality-flag-white.gif|right|70px]]
+|Quality-flag = [[File:quality-flag-green.gif|right|70px]]
-|Status = Seite in Bearbeitung!
+|Status = Seite geprüft, inhaltlich OK
 }}
+[[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]]