Biegebemessung (einachsige Biegung): Unterschied zwischen den Versionen
| Zeile 155: | Zeile 155: | ||
µeds kann abgelesen werden und das aufnehmbare Moment ermittelt werden. | µeds kann abgelesen werden und das aufnehmbare Moment ermittelt werden. | ||
| + | |||
| + | [[Datei:Dimensionslos.PNG]] | ||
===Bemessungstafeln mit dimensionsgebundenen Beiwerten (Kd –verfahren)=== | ===Bemessungstafeln mit dimensionsgebundenen Beiwerten (Kd –verfahren)=== | ||
Version vom 26. April 2016, 11:43 Uhr
Grundlagen
Die Biegebemessung im Grenzzustand der Tragfähigkeit hat die Aufgaben,
nachzuweisen dass der vorab gewählte Betonquerschnitt in der Lage ist die vorhandenen Druckspannungen aufzunehmen und
die erforderliche Stahlquerschnittsfläche der Biegezugbewehrung an den Stellen der maximalen Biegebeanspruchung zu bestimmen.
Um eine Bemessung des Querschnitts im Grenzzustand der Tragfähigkeit zu ermöglichen, werden im Voraus folgende grundlegende Annahmen getroffen:
- Querschnitte, die vor der Verformung eben waren, bleiben eben (Bernoulli Hypothese)
- Es liegt vollkommener Verbund vor, das heißt die Dehnungen des Betons entsprechen den Dehnungen des Betonstahls
- Die Zugfestigkeit des Betons darf im Grenzzustand der Tragfähigkeit nicht berücksichtigt werden, das heißt sämtliche Zugkräfte müssen durch den Betonstahl aufgenommen werden
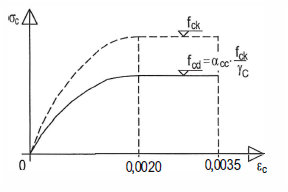
- Für die Spannungs-Stauchungs- Verknüpfung im Beton gilt im Regelfall folgendes vereinfachtes Diagramm:
Gilt für Betone der Festigkeitsklasse bis C50/60 bzw. Leichtbetone bis C50/55
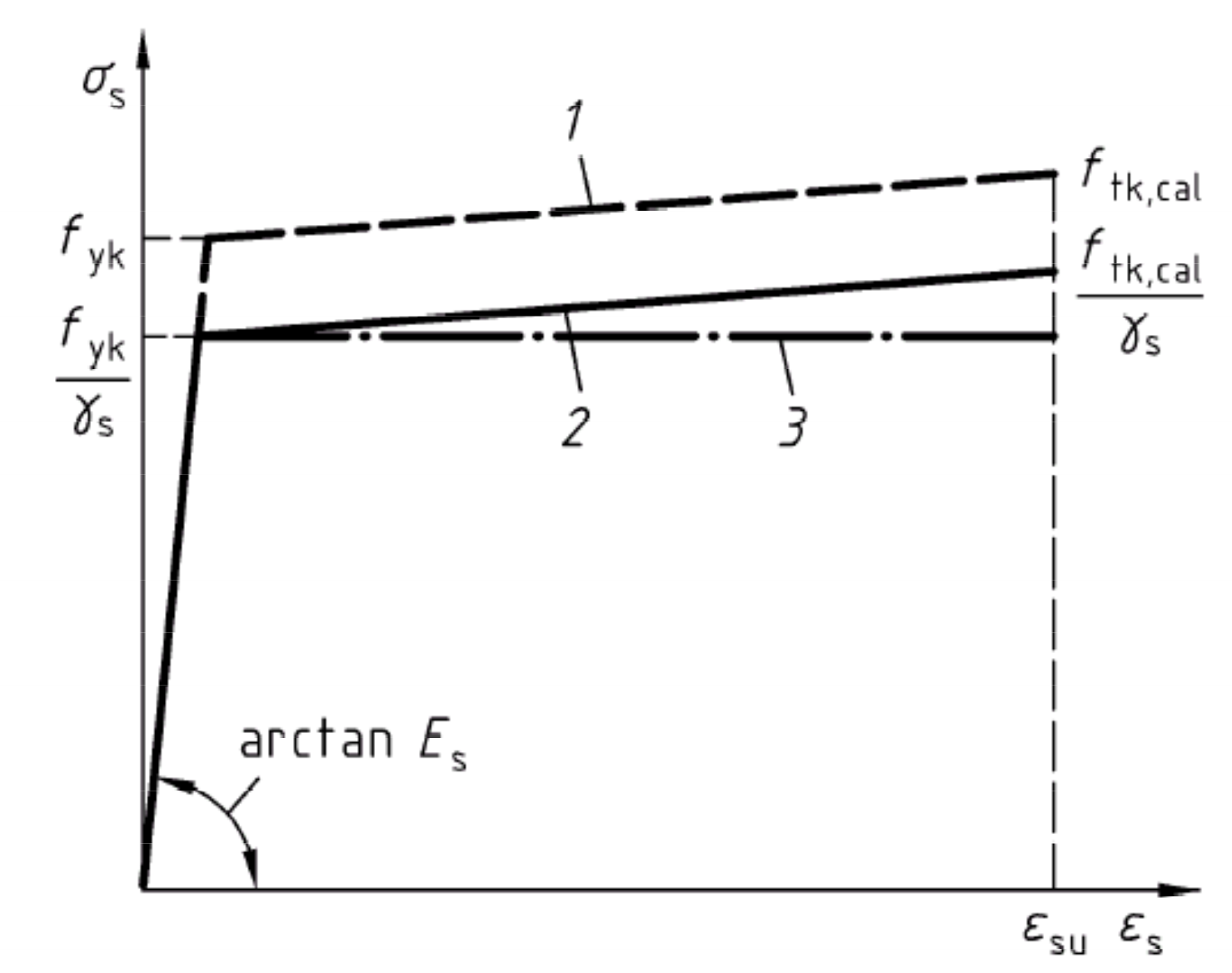
- Die Spannungs-Dehnungs/Stauchungs-Verhältnisse im Stahlbeton werden für die Bemessung wie folgt beschrieben:
Linie I: Zur Vereinfachung wird ein horizontal weiterlaufender Ast angenommen fyk=500N/mm²
Linie II: Ansteigender Ast zugelassen zur Querschnittsbemessung, wenn die Dehnung maximal εud=25 ‰ beträgt
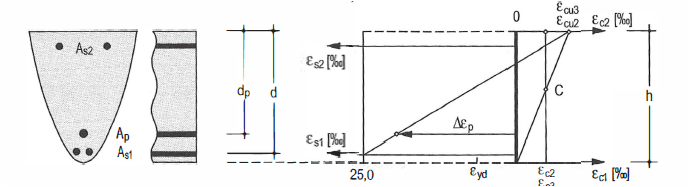
- Es gelten folgende möglichen Dehnungsverteilungen im Stahlbetonquerschnitt
Für Betone bis zur Festigkeitsklasse C50/60 gelten die Grenzstauchungen:
εc2=-3,5‰ bei Biegebeanspruchung und
εc2=εc1=-2,2‰ bei zentrischem Druck
Der Betonstahl versagt bei einer Grenzdehnung von εs1=εs2=25‰
Nachweisführung und Bewehrungsermittlung mit Bemessungshilfen
Eine iterative Handrechnung ist in der Praxis sehr umständlich und daher nicht üblich.
Der Nachweis der Grenztragfähigkeit und die Ermittlung der Längsbewehrung erfolgen im Allgemeinen Bemessungstafeln,
wie sie beispielsweise in [Schneider Bautabellen für Ingenieure 20.Auflage Abs.5.6 Tafeln 1-9] zu finden sind.
Um mit den Bemessungshilfen arbeiten zu können, müssen die Bauteilabmessungen und Materialparameter bekannt sein.
Die statische Nutzhöhe d kann für den Fall, dass sie vor der Bewehrungsermittlung noch unbekannt ist über eine Vorbemessung
abgeschätzt werden und gegebenenfalls nach der Bewehrungswahl noch einmal korrigiert werden und für eine erneute Bemessung verwendet werden.
Mit Hilfe der Bemessungstafeln bzw. Diagrammen kann nun bei bekanntem maximalen einwirkenden Moment die erforderliche Bewehrung,
oder bei bekanntem Bewehrungsquerschnitt das maximal aufnehmbare Moment ermittelt werden.
Um die Verwendung der Hilfsmittel Querschnittsunabhängig und damit allgemein anwendbar zu machen, werden verschiedene dimensionslose bezogene Parameter entwickelt:
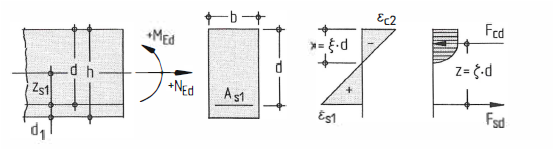
Einwirkende Schnittgrößen müssen auf die mit Hilfe von zs1 auf den Schwerpunkt der Bewehrung übertragen werden:
Meds=Med-Ned*zs1 ( entfällt im Modul S340.de, da keine Normalkraft definierbar)
Das bezogene Moment in der Höhe der gesuchten Bewehrung ergibt sich zu µ Eds=MEds/b*d2*fcd
Die Betondruckkraft Fcd ergibt sich, indem die Fläche der Druckspannungen σcd über die Druckzonenhöhe x integriert wird:
Fcd=∫σcd*b*dz
Mit dem Völligkeitsbeiwert αR, der das Verhältnis der integrierten Fläche zur einhüllenden Rechteckfläche beschreibt, ergbibt sich:
Fcd=αR *b*x*fcd
Es wird eine bezogene Druckzonenhöhe eingeführt: ξ=x/d bzw. x=ξ*d
Fcd=αR*b*ξ*d*fcd oder auch: Fcd/b*d*fcd=αR*ξ
Mit dem Bauteilwiderstand MRds=Fcd * z und der Aussage: Meds=MRds und dem bezogenen Moment:
µEds=MEds/b*d2*fcd = Fcd/b*d²*fcd * z/d
Es wird ein bezogener innerer Hebelarm ζ eingeführt aus:
a=k*x = ka*ξ*d und z= d-a = (1-ka*ξ)*d = ζ * d
a- Abstand von Fcd zur oberen Bauteilkante
Aus allen jetzt bekannten Beziehungen ergibt sich:
µEds= αR*b*ξ*d*fcd/b*d*fcd * (1-ka*ξ)*d/d
⇒ µEds= αR*ξ*ζ
Die Beiwerte αR, ξ und ζ sind von dem Querschnitt des Bauteils unabhängig
und es kann bei gegebenen Dehnungsverhältnis das aufnehmbare Moment mit Hilfe der Tabellen bestimmt werden.
Die erforderliche Bewehrung lässt sich wie folgt ermitteln:
NRd = Fsd-Fcd mit NEd=NRd
⇒ Fsd= Fcd + NEd
Mit bekanntem MEds= Fcd*z ergibt sich:
Fsd= σsd * As unter der Annahme σsd = fyd
⇒ As= 1/fyd * (MEds/z +NEd)
Allgemeines Bemessungsdiagramm
Das allgemeine Bemessungsdiagramm ist für alle Normalbetone bis zur Festigkeitsklasse C50/60 anwendbar.
Als Eingangswert dient entweder das bezogene Moment Müheds=Meds/b*d²*fcd.
Es können alle dazugehörigen Parameter und die Dehnungsverteilung abgelesen werden und die erforderliche Bewehrung mit:
As= 1/fyd * (MEds/z +NEd) ermittelt werden.
Oder, bei bekannter Bewehrungsquerschnittsfläche, der Druckzonenparameter vcd=fyd*As/fcd*b*d.
Damit kann das bezogene Moment abgelesen und die Tragfähigkeit durch umstellen der Formel zu MEds=müh eds*fcd*b*d² ermittelt werden.
Hinweis: Bei Verwendung des Diagramms sind immer geringe Ableseungenauigkeiten zu erwarten
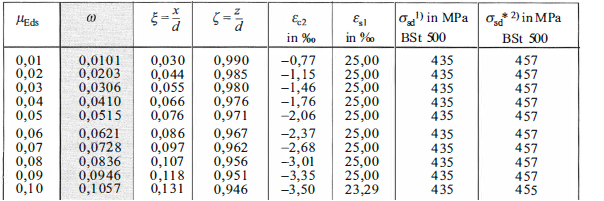
Bemessungstafeln mit dimensionslosen Beiwerten (Omega-Verfahren)
Die Bemessungstafeln zeigen das allgemeine Bemessungsdiagramm in tabellierter Form, erweitert um den Dimensionslosen Beiwert
ω= As*sigma sd-Ned/b*d*fcd
Mit bekanntem Moment dient wieder das bezogene Moment µeds als Einganswert ω kann abgelesen werden
(Entweder ungünstigerer Wert oder interpolieren) und über die Formel As=1/σ sd*(omega*b*d*fcd+Ned) der erforderliche Bewehrungsquerschnitt ermittelt werden.
Bei bekanntem Querschnitt kann durch umstellen der Formel zu ω=As*fyd/fcd*b*d, ω als Eingangswert verwendet werden.
µeds kann abgelesen werden und das aufnehmbare Moment ermittelt werden.