Heißbemessung Stahlbetonbau

Mechamische Einwirkungen

Im EC1-1-2 wird im Brandfall anzunehmenden mechanischen Einwirkungen in direkte und indirekte Einwirkungen unterschieden.

Indirekte Einwirkungen

Indirekte Einwirkungen infolge von Brandbeanspruchung sind Kräfte und Momente, die durch thermische Ausdehnungen, Verformungen und Verkrümmungen hervorgerufen werden. Sie müssen nicht berücksichtigt werden, wenn sie das Tragverhalten nur geringfügig beeinflussen und/oder durch entsprechende Ausbildung der Auflager aufgenommen werden können. Außerdem brauchen sie bei der brandschutztechnischen Bemessung von Einzelbauteilen nicht gesondert verfolgt werden. Wenn indirekte Einwirkungen berücksichtigt werden müssen, sind sie unter Ansatz der thermischen und mechanischen Materialkennwerte aus den baustoffbezogenen Eurocodes zu ermitteln.

Direkte Einwirkungen

Als direkte Einwirkungen werden die bei der Bemessung für Normaltemperatur berücksichtigten Lasten (Eigengewicht, Wind, Schnee usw.) bezeichnet. Die maßgebenden Werte der Einwirkungen sind den verschiedenen Teilen der DIN EN 1991, bzw. den zugehörigen nationalen Anhängen, zu entnehmen, wo auch allgemeine Regeln zur Berücksichtigung von Schnee- und Windlasten sowie Lasten infolge des Betriebes (z.B. Horizontalkräfte infolge von Kranbewegungen) angegeben werden. Eine Verringerung der Belastung durch Abbrand bleibt unberücksichtigt.

Allgemeine Regeln

Für die Einwirkungen gilt die DIN EN1991-1-1/2. Es werden die charakteristischen Lasten wie für die kalte Bemessung angesetzt. Die Einwirkungen im Brandfall Efi,d,t ergeben sich nach den Kombinationsregeln in DIN EN 1990 zu:

$E_{fi,d}=\sum \gamma _{G}\cdot {E_{Gk}}\oplus \gamma _{Q,1}\cdot {\psi _{1,1}}\cdot {E_{Qk,1}}\oplus \sum \gamma _{Q,i}\cdot {\psi _{2,i}}\cdot {E_{Qk,i}}\oplus \sum {A_{d}(t)}$

mit
${{E}_{fi,d}}$ - der Bemessungseinwirkung im Brandfalls
${{G}_{k}}$ - der ständigen, charakteristischen Einwirkungen
${{Q}_{k,1}}$ - der veränderlichen, charakteristischen Leiteinwirkung
${{Q}_{k,i}}$ - der veränderlichen, charakteristischen Einwirkung
${{A}_{d}}(t)$ - dem Bemessungswert der indirekten Einwirkungen
$\gamma _{i}$ - dem Teilsicherheitsbeiwert der Einwirkung nach DIN EN1990
$\psi _{i}$ - dem Kombinationsbeiwert der Einwirkun nach DIN EN1990

Hinweis : Nach DIN EN1992-1-2 NA gelten folgende Erleichterungen für den Kombinationsbeiwert der Leiteinwirkung $\psi _{1,1}$: Es darf $\psi _{1,1}$ durch $\psi _{2,1}$ ersetzt werden, jedoch nur, wenn die Leiteinwirkung nicht der Wind ist.

Vereinfachte Regeln

Wenn indirekte Einwirkungen - also solche, die aus Verformungen im Brandfall resultieren - vernachlässigbar klein sind, gilt vereinfachend die außergewöhnliche Einwirkungskombination als über den Brandverlauf konstant:

${{E}_{fi,d,t}}=E{}_{fi,d}~$

mit
${{E}_{fi,d,t}}$ - der außergewöhnlichen Kombination für den Brandfall (mit den Indizes fire, design, time)
$E{}_{fi,d}$ - der außergewöhnlichen Kombination über den Brandfall konstant

Die Einwirkung während des Brandes kann mittels eines Reduktionsfaktors aus der Einwirkung unter Normaltemperatur ermittelt werden:

${{E}_{fi,d}}={{E}_{d}}\cdot {{\eta }_{fi}}$

mit
${{E}_{fi,d}}$ - der Bemessungseinwirkung während des Brandfalls
${{E}_{d}}$ - der Bemessungseinwirkung bei Normaltemperatur
${{\eta }_{fi}}$ - dem Reduktionsfaktor.

Hinweis : Der Reduktionsfaktor kann vereinfachend und auf der sicheren Seite mit $\eta _{fi}=0,7$ angenommen werden.

Der Reduktionsfaktor lässt sich folgendermaßen ermitteln:

${{\eta }_{fi}}={\frac {{{G}_{k}}+{{\psi }_{fi}}\cdot {{Q}_{k,1}}}{{{\gamma }_{G}}\cdot {{G}_{k}}+{{\gamma }_{Q,1}}\cdot {{Q}_{k,1}}}}$

mit
${{G}_{k}}$ - der ständigen, charakteristischen Einwirkung (mit Index charakteristisch)
${{Q}_{k,1}}$ - der veränderlichen, charakteristischen Leiteinwirkung
${{\gamma }_{G}}$ - dem Teilsicherheitsbeiwert für ständige Einwirkungen
${{\gamma }_{Q,1}}$ - dem Teilsicherheitsbeiwert für veränderliche Leiteinwirkung
${{\psi }_{fi}}$ - dem Kombinationsfaktor für den Brandfall als außergewöhnliche Situation, entspricht ψ2 (quasi-ständig) oder im Ausnahmefall Wind ψ1 (häufig).

Beispielrechnung

Lasten im Brandfall (Bsp.)

Bauteilwiderstände

Für die Widerstandsseite sind die sich bei hohen Temperaturen ändernden Bauteileigenschaften zu beachten. Es gibt zwei Arten von Eigenschaften.

Thermische Eigenschaften

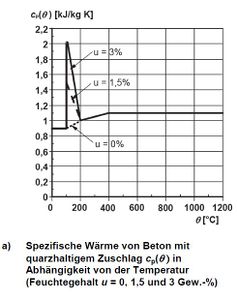
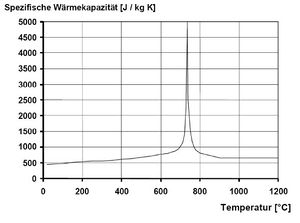
Die thermischen Eigenschaften betreffen die Wärmeleitfähigkeit λc , die spezifische Wärmekapazität c und die Dehnung infolge der Temperaturänderung des Materials.

Die Wärmekapazität beschreibt, wie viel Energie notwendig ist, um das Material um 1K zu erwärmen. Das ist bei Beton stark vom Wassergehalt abhängig. Da Wasser mehr Energie zum erwärmen benötigt als Beton, läuft die Erwärmung des Bauteils am Anfang langsamer ab, bis das Wasser verdampft ist. Bei 100°C verlangsamt sich die Erwärmung aufgrund des Verdampfens des Wassers. Danach ist nur noch der Widerstand des Betons vorhanden. Betonstahl nimmt die Wärme wesentlicher schneller auf als Beton, da die durchschnittliche Wärmekapazität mit 600J/kg K nur halb so hoch ist wie bei Beton. Dadurch erhitzt sich der Stahl schneller als Beton, was zu Spannungen zwischen den Bautstoffen im Bauteil führen kann.

• 

  Spezifische Wärme von Beton nach DIN EN1992-1-2

• 

  Spezifische Wärme von Stahl nach DIN EN1993-1-2

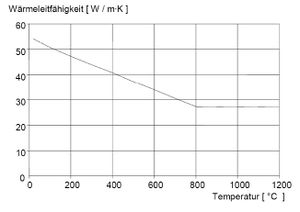
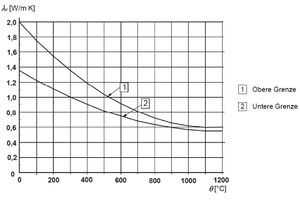
Die thermische Leitfähigkeit beschreibt, wie viel Wärmeenergie in einer bestimmten Zeit durch das Material fließt, also wie schnell die Wärme weitergeleitet wird. Die Leitfähigkeit von Beton nimmt bei steigender Temperatur ab und hängt außerdem stark von Temperaturunterschieden und Zuschlägen ab. Das ist wichtig, um zu ermitteln, wie schnell die Wärme ins Innere des Bauteils dringt und wie schnell dieses wieder abkühlt. Die Wärmeleitfähigkeit von Betonstahl ist deutlich höher als beim Beton. Somit gibt der Stahl die Wärme schneller ab, hier direkt an den Beton. Das führt zu einer schnelleren Erwärmung des Betons.

• 

  Thermische Leitfähigkeit von Beton nach DIN EN1992-1-2

• 

  Thermische Leitfähigkeit von Stahl nach DIN EN1993-1-2

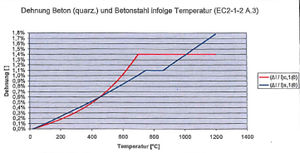
Die thermische Dehnung beschreibt, wie sich Beton und Stahl bei hohen Temperaturen ausdehnen. Je höher die Temperatur ist, desto stärker ist die Dehnung. Da sich Beton und Stahl aber nicht in gleicher Weise ausdehnen, kommt es zu inneren Spannungen im Bauteil. Diese können bei sehr hohen Temperaturen erheblich sein und müssen bei der Bemessung beachtet werden. Folgendes Diagramm stellt die Dehnung des Materials in Bezug auf die Bauteiltemperatur dar.

• 

  Thermische Dehnung von Beton und Betonstahl in Abhängigkeit der Temperatur

Mechanische Eigenschaften

Die mechanischen Eigenschaften spiegeln sich in der Spannungs-Dehnungsbeziehung der Baustoffe wieder.
Unter hohen Temperaturen verändern sich die Materialfestigkeiten und die E-Module von Beton und Stahl. Die Dehnung unter hohen Temperaturen nimmt schon bei geringem Spannungszuwachs deutlich zu. Daraus ergibt sich wiederum, dass die Festigkeit von Beton und Stahl unter hohen Temperaturen abnimmt.
Beton
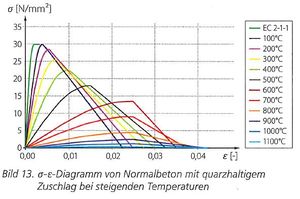
Die Spannungs-Dehnungsbeziehung beim Beton wird durch zwei Parameter bestimmt, die Druckfestigkeit fc,θ und die Stauchung εc1,0 (abzulesen am abfallenden Kurventeil).
Ein weiterer Einflussfaktor ist der verwendete Zuschlagsstoff. Unterschieden werden muss hier zwischen quarzhaltigen und kalksteinhaltigen Zuschlägen. Das Diagramm ist für quarzhaltige Zuschläge aufgestellt, da diese Werte im Gegensatz zu den kalksteinhaltigen Zuschlägen geringer ausfallen. Die Tabelle 3.1 im EC2-1-2 gibt die Hauptparameter für die beiden Zuschlagsstoffe an. (siehe auch Materialeigenschaften von Beton und Stahl (aus Abschnitt 3, EC 2-1-2))
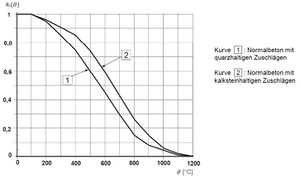
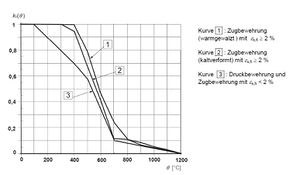
Diese Abnahme der Festigkeiten wird im EC2 mit Reduktionsbeiwerten berücksichtigt. Bei Beton ist der Beiwert kc,θ für die Betondruckfestigkeit abhängig von der Bauteiltemperatur und dem Zuschlagsstoff. Der Beiwert kann aus dem unten stehenden Diagramm aus der DIN EN 1992 Abs. 4.2.4.2 entnommen werden. Außerdem ist zu beachten, dass die Zugfestigkeit des Betons bei steigender Temperatur sehr stark abnimmt und damit nicht mehr zum Ansatz gebracht werden kann. Dies gilt vor allem für die Bereiche zwischen den Rissen in den äußeren Bewehrungslagen.
Durch die Abnahme des E-Moduls nimmt die Verformungsfähigkeit von 2,5‰ bei 20°C auf 10-20‰ bei 600°C zu, was zu einer ständigen Umlagerung von Spannungen führt. Daraus resultiert der Abfall der aufnehmbaren Druckfestigkeit.

• 

  Spannungs-Dehnungs-Diagramm von Beton bei steigenden Temperaturen

• 

  Beiwert zur Berücksichtigung des Abfalls der caharakteristischen Druckfestigkeit von Beton

Betonstahl
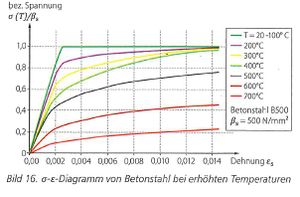
Die Spannungs-Dehnungsbeziehung beim Betonstahl ist abhängig von der Dehnung und der Temperatur. Bei Stahl spielt die Herstellung eine entscheidende Rolle. Es wird unterschieden zwischen warm- und kaltgewalztem Stahl. Die Tabellen 3.2 im EC2-1-2 geben die Parameter für beide Herstellungsarten an.
Da sich der Betonstahl unter Hitzeeinwirkung ausdehnt und gleichzeitig an Festigkeit verliert, wurde im EC2-1-2 eine kritische Stahltemperatur festgelegt. Diese liegt beim Betonstahl B500 bei 500°C und liegt auf der sicheren Seite. Dabei ist die kritische Dehngeschwindigkeit ε’=10-4 s-1 nur von der Stahlsorte und dem Belastungsgrad abhängig, jedoch nicht von der Erwärmungsgeschwindigkeit, wodurch die kritische Temperatur generell festgelegt werden kann. Analog zum Beton gibt es für Betonstahl auch einen Reduzierungsfaktor ks für die charakteristische Festigkeit fyk in Abhängigkeit zur Stahltemperatur.

• 

  Spannungs-Dehnungs-Diagramm von Stahl bei steigenden Temperaturen

• 

  Beiwert zur Berücksichtigung des Abfalls der caharakteristischen Druckfestigkeit von Betonstahl

Materialeigenschafen aus EC2-1-2

Eine tabellarische Übersicht über die Materialeigenschaften aus dem EC2-1-2 Abschnitt 3 ist hier zu finden.
Detaillierte Informationen zu den Materialkennwerten aus dem EC sind hier zu finden.
Detaillierte Informationen zu den Abminderungsbeiwerten für Beton und Betonstahl aus dem EC sind hier zu finden.

Bemessungsverfahren im Stahlbetonbau nach EC 2-1-2

Im EC2 werden drei Nachweisverfahren angegeben, die sich in einzelne Verfahren unterteilen lassen. Grundlage der Nachweise sind die mechanischen und thermischen Eigenschaften sowie die Einheitstemperaturkurve. Die Ermittlung der Lasten erfolgt nach den bekannten Regeln.

Stufe 1: Tabellenverfahren

Beim Bemessungsverfahren mithilfe tabellarischer Daten werden in der Regel Querschnittsabmessungen des zu untersuchenden Bauteils verglichen. Die tabellarischen Daten wurden aus den sogenannten Normbrandversuchen ermittelt. Die im EC2-1-2, Abschnitt 5 enthaltenen Tabellen stellen die Mindestwerte der Querschnittsabmessungen und Achsabstände der Bewehrung in Abhängigkeit von der Feuerwiderstandsdauer dar. Die Daten sind bis zu einer Widerstandsdauer von 240 Minuten tabelliert und liegen stehts auf der sicheren Seite.

Hinweis : Die Tabellenwerte gelten für Normalbeton (2 000 bis 2 600 kg/m³, siehe EN 206-1) mit quarzhaltigen Zuschlägen. Werden in Balken oder Platten kalksteinhaltige Zuschläge verwendet, darf die Mindestabmessung des Querschnitts um 10 % verkleinert werden. Bei Anwendung der Tabellenwerte brauchen keine weiteren Überprüfungen hinsichtlich Schub- und Torsionstragfähigkeit und Verankerung der Bewehrung (EC2-1-2, siehe Absch. 4.4 ) durchgeführt werden. Bei Anwendung der Tabellenwerte brauchen mit Ausnahme der Oberflächenbewehrung ( EC2-1-2, siehe Absch. 4.5.1 ) keine weiteren Überprüfungen hinsichtlich des Abplatzens durchgeführt werden.

Der Eurocode 2-1-2 enthält Bemessungstabellen für:

1. Stützen mit Rechteck- oder Kreisquerschnitten bei ein- und mehrseitiger Brandbeanspruchung: Methode A, Methode B
2. tragende und nichttragende Wände.
3. Balken mit Rechteck- und I-Querschnitt bei drei- oder vierseitiger Brandbeanspruchung.
4. ein- oder zweiachsig gespannte Platten, Durchlaufplatten, Flachdecken und Rippendecken.

Stufe 2: vereinfachte Verfahren

Es ist bekannt, dass sich bei Brandbeanspruchung die Materialeigenschaften, bsw. die Tragfähigkeit, in Abhängigkeit der Temperaturen verringern. Die in EC 2-1-2 enthaltenen vereinfachten Rechenverfahren beschreiben die Verringerung der Tragfähigkeit von Bauteilen unter Brandbeanspruchung annähernd durch eine temperaturabhängige Verkleinerung des Querschnitts und eine temperaturbedingte Abminderung der Materialeigenschaften beim Brand.

Eine Verringerung des Betonquerschnitts berücksichtigt, dass die äußeren Betonoberflächen, die dem Brand direkt ausgesetzten sind, aufgezehrt werden und für die Tragfähigkeit nicht mehr angesetzt werden können. Um den Tragfähigkeitsnachweis, analog dem Nachweis für Normaltemperatur nach DIN EN 1992-1-1, zu führen, muss für den gedanklich verringerten Betonquerschnitt lediglich die Festigkeit von Beton und Bewehrungsstahl temperaturabhängig mit den Beiwerten K_c(θ) bzw. K_s(θ) abgemindert werden.

Zur Ermittlung der benötigten Querschnittstemperaturen können die zusammengestellten Diagramme mit Temperaturprofilen im EC 2-1-2 (Anhang A) verwendet werden. Diese Profile dürfen nur für Wände, Platten, Balken und Stützen mit den üblichen Querschnittsformen bei Brandbeanspruchung nach der Einheitstemperaturzeitkurve angewendet werden. Nachdem die reduzierten Betonquerschnitte und die temperaturabhängigen Abminderungen der Betonfestigkeit bestimmt wurden, stehen nach EC 2-1-2 Anhang B zwei Verfahren zur Bemessung zur Verfügung.

• Zum einen gibt es die Zonenmethode (nach EC 2-1-2 Anhang B.2), die für Druckglieder im nationalen Anwendungsdokument nur mit zusätzlichen Ausnahmen nach Cylok und Achenbach geführt werden darf.

Hinweis : Die Zonenmethode darf für Bauteile, die auf Biegung mit oder ohne Normalkraft beansprucht werden, ohne zusätzliche Annahmen angewandt werden.

• Zum anderen gibt es die sogenannte 500 °C- Isothermen-Methode im Anhang B.1, die nach nationalem Anhang für die Anwendung in Deutschland nicht zugelassen ist.

Achtung : In den informativen Anhängen C bis E werden noch weitere vereinfachte Rechenverfahren angeboten. Hiervon dürfen gemäß EC2-1-2 in Deutschland nur die Verfahren im Anhang E für statisch bestimmt gelagerte und durchlaufende Balken und Platten angewandt werden, bei denen die Tragfähigkeit im Brandfall wesentlich durch temperaturabhängige Festigkeitsabnahme und die kritische Temperatur der Feldbewehrung bestimmt wird.

Varianten des vereinfachten Verfahrens

Temperaturprofile (aus Anhang A des EC 2-1-2)
Zonenmethode nach DIN EN 1992-1-2
Isothermen-Methode nach DIN EN 1992-1-2
Erweiterte Zonenmethode nach Cyllok und Aschenbach

Stufe 3: allgemeine Verfahren

Bei dem allgemeinen Rechenverfahren wird über eine rechnerische Simulation das Trag- und Verformungsverhalten brandbeanspruchter Einzelbauteile, Teil- oder Gesamttragwerke mit beliebigen Querschnittsformen, bei voller oder lokaler Temperaturbeanspruchung, ermittelt. Es erfordert, im Vergleich zum tabellarischen Nachweis oder zum vereinfachten Rechenverfahren, einen größeren Aufwand in der Berechnung. Außerdem ist die Prüfbarkeit der Ergebnisse nur mit einer Gegenrechnungen zu kontrollieren.

Insbesondere für eine statisch unbestimmte Konstruktion, bei denen das Verhalten des Gesamtsystems nicht durch Versuche am Teilsystem bestimmt werden kann, ist die numerische Modellierung und rechnerische Nachweisführung praktisch die einzige Möglichkeit, die Feuerwiderstandsdauer des Tragwerks zu bestimmen. Gerade wegen des Anspruchs der Allgemeingültigkeit und die Korrektheit müssen die allgemeinen Rechtsverfahren kritisch überprüft werden.

Neben einer möglichen Inkorrektheit des Programms, können Eingabedaten problemspezifisch nicht richtig oder nicht sinnvoll für zutreffende Bemessungsereignisse eingegeben werden. Sofern als Rechengrundlage nicht die richtigen Materialgesetze oder Brandbeanspruchung im Programmcode fest hinterlegt sind, können ebenfalls gravierende Abweichungen entstehen.
Aus diesem Grund wurde im nationalen Anhang CC zur DIN EN 1991-1-2/NA Validierungs- und Testbeispiele auf Basis eines Abschlussberichtserstellt, mit denen die Überprüfung der Anwendbarkeit des Rechenprogramms, für die die brandschutztechnische Bemessung von Bauteilen und Tragwerken, möglich ist. Damit ist ein Rückschluss auf reale Tragwerke umsetzbar. Für mehr Informationen zum Thema Validierung von Rechenprogrammen siehe:

Hinweis : Der nationale Anhang CC sieht vor, dass vom Ersteller eines Rechenprogramms zur Durchführung von Nachweisen nach den allgemeinen Rechenverfahren, vor der Anwendung des Programms für bauordnungsrechtliche relevante Brandschutznachweise, die Validierungsbeispiele eigenständig berechnet werden sollen. Diese Musterberechnung soll, unter Verwendung der im Anhang CC enthaltenen tabellarischen Übersichten, die im Rahmen der Validierung durch den Programmhersteller erzielten Ergebnisse in einer Dokumentation erstellt werden und dem Prüfingenieur bzw. Prüfsachverständigen neben den geführten Nachweisen in einer Dokumentation vorgelegt werden. Eine Abweichung von Musterergebnissen sollte innerhalb der angegebenen Grenzbereiche liegen.

Die Berechnung erfolgt in zwei Schritten:
Der erste Schritt ist die thermische Analyse. Dabei werden die Temperaturverteilung und die Temperaturentwicklung innerhalb des betrachteten Bauteils mittels Finiten Elementen ermittelt. Somit ergeben sich zum einen die Brandgaszeittemperaturen, aus denen die Temperaturzeitkurve ermittelt wird. Zum anderen ergeben sich daraus die Isothermen, mit denen die Bauteiltemperaturen ermittelt werden können. Diese geben, im Gegensatz zu den Tabellen des Anhangs A in EC2-1-2, den Zustand des konkret vorliegenden Bauteils an.
Weiterführende Informationen für die thermische Analyse sind hier zu finden.

Der zweite Schritt ist die mechanische Analyse. Dabei wird das Trag- und Verformungsverhalten unter Brandbeanspruchung untersucht. Das Ziel ist die Ermittlung der mechanischen Einwirkung Efi,d,t und der temperaturabhängigen Beanspruchbarkeit Rfi,d,t. Die Einwirkungen resultieren aus äußeren Belastungen, thermischen Einwirkungen wie Zwängungen aufgrund unterschiedlicher Erwärmung des Bauteils, und nichtlinearen Einflüssen aus der Berechnung nach Theorie II. Ordnung.
Der Nachweis wird auf Grundlage der ermittelten Informationen nach den üblichen Bedingungen der Kaltbemessung durchgeführt. Grundsätzlich gilt auch hier:   Ed,fi < Rd,fi
Weiterführende Informationen für die mechanische Analyse sind hier zu finden.

Nebenwirkungen bei Brandbeanspruchung

Betonabplatzungen

Unter schnell ansteigenden Temperaturen steigt die Gefahr, dass Teile der äußeren Schichten eines Stahlbetonbauteils abplatzen. Das gebundene Wasser im Beton geht bei steigender Temperatur in den gasförmigen Zustand über und versucht aus dem Beton zu entweichen. Kann der Wasserdampf aufgrund von dichtem Betongefüge nicht schnell genug entweichen, beispielsweise bei hochfesten Betonen, erhöht sich die Wahrscheinligkeit von Betonabplatzungen. Die größte Gefahr tritt in den ersten 10 bis 30 Minuten auf, weil in diesem Zeitraum der größte Temperaturanstieg zu verzeichnen ist.
Bei Normalbeton ist die Wahrscheinlichkeit für Betonabplatzungen auf dünne Bauteile begrenzt. Für Betondeckungen über 60mm sollte Netzbewehrung eingelegt werden. Um das Abplatzen bei hochfestem Beton zu vermeiden, sollten dem Beton Fasern beigefügt werden.
Betonabplatzung nach EC2-1-2 Abschnit 4.5

Einfluss der Dehnunen auf das statische System

Da die starken Dehnungen, sowohl des Betons als auch des Stahls, große Verformungen und Zwängungen verursachen, sind diese besonders zu berücksichtigen. Sie verstärken die Rissbildung in Zustand II. Außerdem ist eine realistische Erfassung der Verformungen bei Bauteilen notwendig, die nach Theorie II. Ordnung berechnet werden, wie zum Beispiel Stützen. Die Dehnungen und die daraus resultierenden Verformungen werden durch die Theorie II. Ordnung zusätzlich verstärkt, was zu großen Verschiebungen am System führt und damit auch zu hohen Schnittkräften.
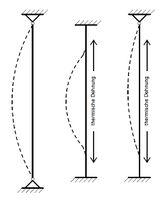
Wenn man eine Pendelstütze unter Brandbeanspruchung beobachtet, versucht diese sich auszudehnen. Das führt bei Stützen zwischen zwei Geschossen zu einer Einspannung am Kopf und Fuß der Stütze, da sie sich in der Länge nicht frei bewegen kann. Diese Veränderung des Systems bewirkt eine neue Knicklänge von der halben Stützenlänge und sollte daher unbedingt in den Bemessungen einer solchen Pendelstütze berücksichtigt werden.
Unabhängig vom Bauteiltyp verursachen die Dehnungen bei nichtsymmetrischer Beflammung Spannungen innerhalb des Bauteils. Durch die unterschiedliche Erwärmung der Seiten behindern sich die Bereiche gegenseitig in der Ausdehnung, wodurch Kräfte freigesetzt werden. Bei Kragstützen führt das beispielsweise bei dreiseitiger Beanspruchung zu einer verstärkten Biegung.

Einspannung von Pendelstützen im Brandfall

Einspannung einer Pendelstütze im Brandfall

Nach EC2-1-2 NA AA.4 darf die Einspannung im Brandfall bei Pendelstützen angesetzt werden. Die Einspannung ist als volle Einspannung anzusehen. Die Erleichterung gilt nur für Stahlbetonstützen in ausgesteiften Gebäuden.
Es wird zwischen Dachgeschossen und Zwischengeschossen unterschieden.
Für Zwischengeschosse (Regelgeschosse) gilt für die Knicklänge im Brandfall: $l_{o,fi}=0,5\cdot {l}$
Für andere Geschosse, beispielsweise Dachgeschosse, gilt für die Knicklänge im Brandfall: $l_{o,fi}=0,7\cdot {l}$.

Berechnung von Stahlbetonbauteilen mit Softwarelösungen

Die plausiblen Eingaben der Parameter in die Berechnungsprogramme ist bei der Bemessung von Stahlbetonbauteilen entscheidend für das Ergebnis. Insbesondere bei der Heißbemessung haben kleine Änderungen große Auswirkungen auf beispielsweise die erforderliche Bewehrung.
Bei Stahlbetonstützen ist aufgrund des statischen Systems die Empfindlichkeit auf Ausmitten und Steifigkeiten generell sehr hoch. Bei der Heißbemessung von Stahlbetonstützen verstärkt sich der Effekt noch weiter. Durch die Reduzierung der Steifigkeiten und Druck- bzw Zugfestigkeiten von Beton und Stahl ergeben sich bei der Berechnung mittels Theorie II. Ordnung nochmal größere Verformungen. Diese erzeugen widerum größere Schnittkräfte, die von dem Material aufgenommen werden müssen. Nun hat zum Beispiel der Stahl in einer Stütze nicht überall die gleiche Temperatur und somit auch nicht die dieselbe Tragfähigkeit. Insofern ist die Anordnung der Bewehrung entscheidend für das Ergebnis der Berechnung. Doch insbesondere hier bieten Softwarelösungen meistens viele Varianten der Bewehrungsanordnung, die genau betrachtet werden müssen, um wirtschaftliche Ergebnisse zu erzielen.
Drei Einstellungsmöglichkeiten sollten bei einer Heißbemessung von Stahlbetonstützen immer überprüft werden:
Betondeckung
Die Betondeckung ist die Schutzschicht für den Bewehrungsstahl. Je höher die Betondeckung ist, desto geringer ist die Temperatur im Stahl und somit gewinnt das Material an Tragfähigkeit. Die Erhöhung der Betondeckung verschiebt die Bewehrung also ins Innere der Stütze, wobei die Temperatur stark abnimmt. Das kann schon bei geringen Veränderungen große Auswirkungen haben, da der Anstieg der Temperatur am Stützenrand extrem steil ist (siehe Bild).

Bewehrungswahl

1. Bewehrung über den Umfang verteilen
2. zusätzliche Bewehrung manuell mittig zum Randbereich der Stütze einlegen
3. Die Bewehrung mehr in der Mitte der Stütze konzentrieren

Durch die starke Reduzierung der Lasten kann das Knicken in beide Richtungen maßgebend werden, sodass die eingelegte Eckbewehrung oder die einseitige Bewehrung die Belastung nicht mehr aufnehmen können. Außerdem nimmt die Temperatur zur Mitte der Stütze hin ab und die Festigkeit des Betonstahls wird weniger reduziert. Somit werden Bewehrungswahlen, die für die kalte Bemessung hilfreich sind, für die Heißbemessung ungünstig. Auf der sicheren Seite für die Heißbemessung ist immer eine umfangverteilte Bewehrung mit möglichst mittig liegenden Eisen. (Bild)

Statisches System
Eine Stütze verändert unter Brandbeanspruchung zum Teil sein statisches System. Zum einen lässt die Einspannung bei Pendelstützen eine Reduzierung der Knicklänge um 50% zu. Zum anderen ist zu untersuchen, ob bei Kragstützen eine teilweise Einspannung am Stützenkopf möglich ist, beispielsweise durch Stahlbetonbinder bei großen Hallensystemen. Diese Erleichterungen können bei der Bemessung auf jeden Fall berücksichtigt werden, müssen aber meistens manuell bei der Software ausgewählt bzw. angegeben werden. (Bild mbaec auswahl, Bild Einspannung)