Verankerung am Kragarmende (Bsp.): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
Berechnungsbeispiel zur Verankerung am Kragarmende | Berechnungsbeispiel zur Verankerung am Kragarmende | ||
| + | |||
| + | == Kontext == | ||
| + | |||
| + | In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Ende eines Kragarms nachzuweisen. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zum Kragarmende finden sich [[Verankerungslänge#Verankerung_am_Kragarmende|hier]] | ||
| + | |||
== Aufgabenstellung == | == Aufgabenstellung == | ||
| Zeile 6: | Zeile 11: | ||
[[File:Verankerung am Kragarmende (Bsp.) 2.JPG|rahmenlos|rand|tumb|250px|Baustatik-Wiki]] | [[File:Verankerung am Kragarmende (Bsp.) 2.JPG|rahmenlos|rand|tumb|250px|Baustatik-Wiki]] | ||
| + | '''Schnitt noch überprüfen, untere Bewehrung''' | ||
| − | Für den dargestellten Träger mit Kragarm ist die Verankerungslänge am Kragarmende zu bestimmen. Gegeben sind folgende Daten: | + | Für den dargestellten Träger mit Kragarm ist die Verankerungslänge am Kragarmende zu bestimmen. |
| + | |||
| + | Gegeben sind folgende Daten: | ||
* Beton: <math>C30/37</math> | * Beton: <math>C30/37</math> | ||
| Zeile 35: | Zeile 43: | ||
=== Randzugkraft === | === Randzugkraft === | ||
| − | Die Randzugkraft wird hier über das Verschieben der Zugkraftlinie um das Versatzmaß <math>a_L</math> ermittelt. Dazu wird das Moment an der Stelle <math>x_0</math> berechnet. | + | Die Randzugkraft wird hier über das [[Verankerungslänge#Ermittlung_der_Randzugkraft_durch_Verschieben_der_Momentenlinie|Verschieben der Zugkraftlinie]] um das Versatzmaß <math>a_L</math> ermittelt. Dazu wird das Moment an der Stelle <math>x_0</math> berechnet. |
<math>p_{Ed} = 1,35 \cdot 40 kN/m + 1,5 \cdot 25 kN/m = 91,5 kN/m</math> | <math>p_{Ed} = 1,35 \cdot 40 kN/m + 1,5 \cdot 25 kN/m = 91,5 kN/m</math> | ||
| Zeile 88: | Zeile 96: | ||
<math>l_{bd} = 42,45 cm \leq 45,00 cm = l_{b,vorh}</math> | <math>l_{bd} = 42,45 cm \leq 45,00 cm = l_{b,vorh}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Version vom 2. Mai 2022, 07:37 Uhr
Berechnungsbeispiel zur Verankerung am Kragarmende
Kontext
In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung am Ende eines Kragarms nachzuweisen. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zum Kragarmende finden sich hier
Aufgabenstellung
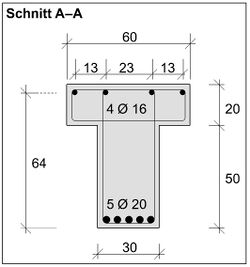
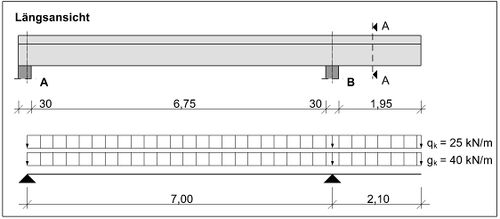
Für den dargestellten Träger mit Kragarm ist die Verankerungslänge am Kragarmende zu bestimmen.
Gegeben sind folgende Daten:
- Beton:
- Betondeckung:
- Nutzhöhe obere Bewehrungslage:
- Gewählte Bewehrung oben am Kragarmende:
- Druckstrebenneigungswinkel: ° →
Lösung
Verbundfestigkeit
Bewehrung oben → mäßiger Verbund
→ C30/37 →
Versatzmaß
Bei seitlich ausgelagerter Bewehrung ist das Versatzmaß um den Abstand der ausgelagerten Stäbe vom Stegrand zu erhöhen. Dieser Wert beträgt hier .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_L = z \cdot (cot {\theta} + cot {\alpha})/2 + x}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_L = 57,6 cm \cdot (3,0 + 0)/2 + 10 cm = 96,4 cm}
Randzugkraft
Die Randzugkraft wird hier über das Verschieben der Zugkraftlinie um das Versatzmaß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_L} ermittelt. Dazu wird das Moment an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_0} berechnet.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_{Ed} = 1,35 \cdot 40 kN/m + 1,5 \cdot 25 kN/m = 91,5 kN/m}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D_{min} = 4 \cdot \O_s = 4 \cdot 1,6 cm = 6,4 cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_0 = c_{nom} + \O_s + D_{min}/2 = 5,0 cm + 1,6 cm + 6,4 cm / 2 = 9,8 cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed,x0} = p_{Ed} \cdot \frac{(x_0 + a_L)^2}{2} = 91,5 kN/m \cdot \frac{(0,098 m + 0,964 m)^2}{2} = 51,60 kNm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = \frac{M_{Ed,x0}}{z} = \frac{51,60 kNm}{0,576 m} = 89,58 kN}
Erforderliche Bewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = \frac{F_{sd}}{f_{yd}} = \frac{89,58 kN}{43,5 kN/cm^2} = 2,06 cm^2}
Stahlspannung
Vorhanden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2 \O 16} → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 4,02 cm^2}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5 kN/cm^2 \cdot \frac{2,06 cm^2}{4,02 cm^2} = 22,28 kN/cm^2}
Grundwert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}} = \frac{1,6 cm}{4} \cdot \frac{22,28 kN/cm^2}{0,21 kN/cm^2} = 42,45 cm}
Bemessungswert der Verankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = {\alpha}_1 \cdot {\alpha}_3 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
Formgebung: Gerades Stabende → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 1,0}
Querbewehrung: Vernachlässigbar → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_3 = 1,0}
Angeschweißte Querstäbe: Keine → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_4 = 1,0}
Querdruck: Nicht vorhanden → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5 = 1,0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = 1,0 \cdot 1,0 \cdot 1,0 \cdot 1,0 \cdot 42,45 cm = 42,45 cm}
Mindestverankerungslänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 1,0 \cdot 1,0 \cdot 1,0 \cdot \left( \frac{1,6 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,21 kN/cm^2} \right) \\ 10 \cdot 1,0 \cdot 1,6 cm \end{matrix}} \right\} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 24,86 cm \\ 16 cm \end{matrix}} \right\} }
Nachweis der Verankerungslänge
Als Verankerungslänge soll hier gewählt werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,vorh} = 45 cm} .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = 42,45 cm \leq 45,00 cm = l_{b,vorh}}