Biegebemessung (einachsige Biegung): Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) |
EWill (Diskussion | Beiträge) |
||
| Zeile 93: | Zeile 93: | ||
==Grundsätzliche Annahmen== | ==Grundsätzliche Annahmen== | ||
| − | Die folgenden Voraussetzungen werden der Biegebemessung zugrunde gelegt: | + | Die folgenden Voraussetzungen werden der Biegebemessung zugrunde gelegt<ref Name = "Q5">DIN EN 1992-1-1, Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2011</ref>: |
<ul> | <ul> | ||
<li>Die Hypothese von Bernoulli gilt, d.h. dass die angenommen wird, dass die Dehnungen linear über den Querschnitt verteilt sind (Ebenbleiben der Querschnitte). Diese Annahme gilt für schlanke ist für schlanke Bauteile erfüllt (l/h$\geq$2 bzw. für Kragträger $l_k\geq1$), nicht erfüllt ist sie in Bereichen mit konzentrierter Lasteinleitung (z. B. unter Einzellasten oder im Auflagerbereich). Für Bereiche in denen nicht davon ausgegangen werden kann, dass die Dehnungen linear über den Querschnitt verteilt sind, müssen andere Bemessungsverfahren verwendet werden z.B. Stabwerkmodelle.</li> | <li>Die Hypothese von Bernoulli gilt, d.h. dass die angenommen wird, dass die Dehnungen linear über den Querschnitt verteilt sind (Ebenbleiben der Querschnitte). Diese Annahme gilt für schlanke ist für schlanke Bauteile erfüllt (l/h$\geq$2 bzw. für Kragträger $l_k\geq1$), nicht erfüllt ist sie in Bereichen mit konzentrierter Lasteinleitung (z. B. unter Einzellasten oder im Auflagerbereich). Für Bereiche in denen nicht davon ausgegangen werden kann, dass die Dehnungen linear über den Querschnitt verteilt sind, müssen andere Bemessungsverfahren verwendet werden z.B. Stabwerkmodelle.</li> | ||
| Zeile 102: | Zeile 102: | ||
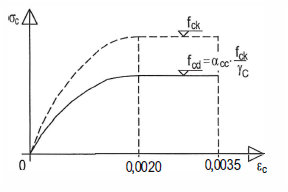
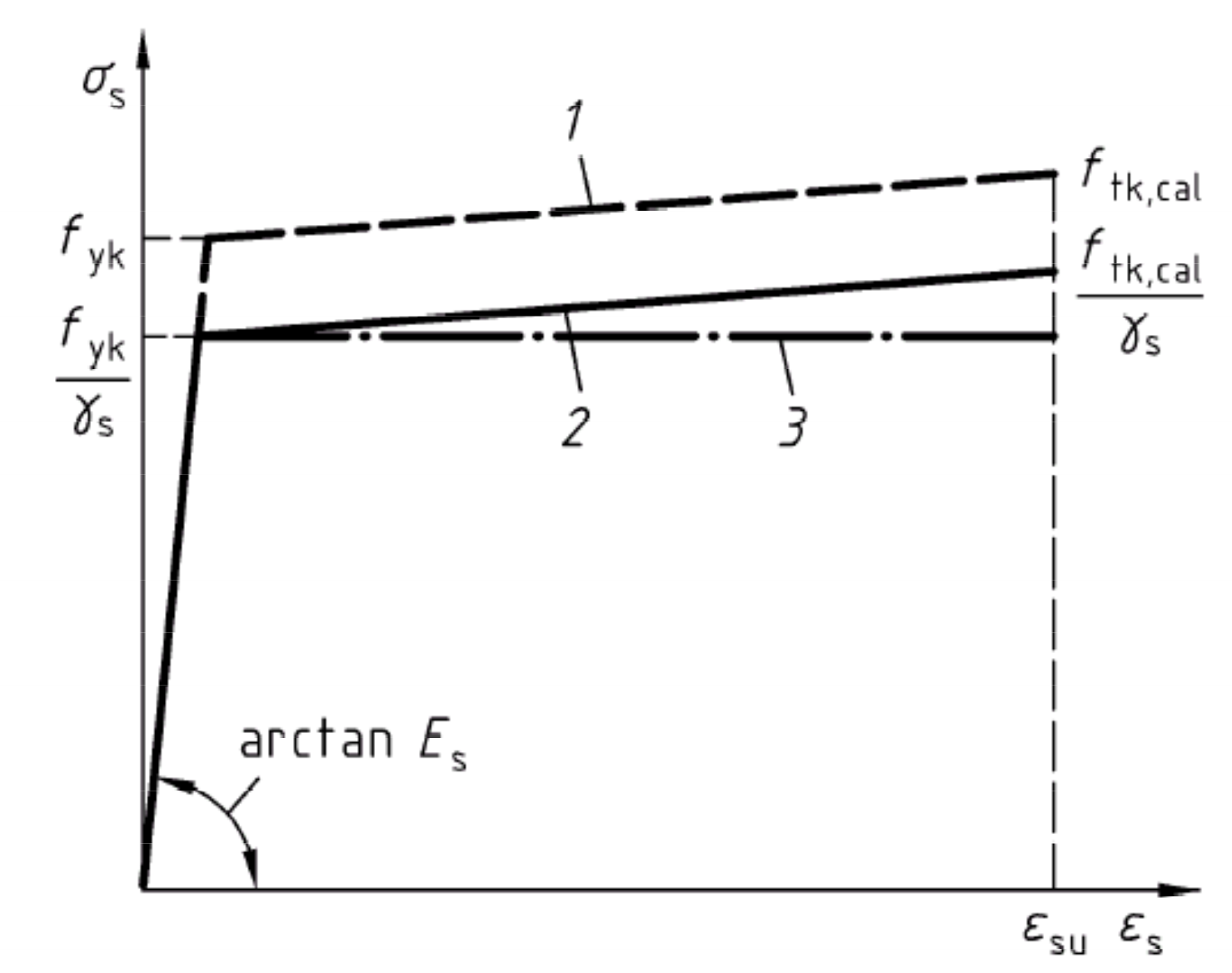
<li>Für die Spannungsdehnungslinie des Betons und der Bewehrung gelten die Zusammenhänge aus Bild … und Bild ….</li> | <li>Für die Spannungsdehnungslinie des Betons und der Bewehrung gelten die Zusammenhänge aus Bild … und Bild ….</li> | ||
| + | </ul> | ||
| + | Die Ermittlung des Bauteilwiderstands erfolgt durch Variation der Dehnungsebenen, bis sich innere und äußere Schnittgrößen im Gleichgewicht befinden. Da dies ein iterativer Prozess ist, der bei einer Handrechnung einen hohen Aufwand bedeutet, werden i.d.R Bemessungshilfsmittel verwendet, diese können gängigen Tabellenwerekn z.B. Schneider Bautabellen<ref Name = "Q4">Albert,A., Bautabellen fü Ingenieure, Auflage 26, Bundesanzeigerverlag, 2024</ref> entnommen werden. Für die Erstellung von Bemessungshilfsmitteln bietet sich die Verwendung von dimensionslosen Beiwerten an. | ||
| + | |||
| + | Im Folgenden werden das allgemeine Bemessungsdiagramm, das $\omega$-Verfahren und das $k_d$-Verfahren. Anschließend findet auch noch eine Herleitung der Gleichungen für die Biegebemessung mit einem parabel-rechteckförmigen Spannungsverlauf in der Druckzone (iterative Lösung) und mit dem vereinfachten rechteckförmigen Spannungsblock (geschlossene Lösung) statt. | ||
| + | |||
| + | ==Druckbewehrung== | ||
| + | |||
| + | Durch die Anordnung einer Druckbewehrung wird die Betondruckzone entlastet und die Druckzonenhöhe reduziert bzw. nicht mehr gesteigert. | ||
| + | In der Regel kann bei der Bemessung trotz der Druckbewehrung mit der Bruttofläche der Betondruckzone gerechnet werden, da die Unterschiede im Vergleich zur Bemessung mit der Nettofläche gering sind<ref name = "Q2"></ref>. | ||
| − | < | + | Für Rechteckquerschnitte mit Druckbewehrung stehen ebenfalls Bemessungshilfsmittel zur Verfügung<ref name = "Q4"></ref>. Es können auch die Bemessungshilfsmittel für Rechteckquerschnitte ohne Druckbewehrung verwendet werden, dabei ist dann das einwirkende Moment aufzuteilen (vgl. Bild …). |
| + | |||
| + | Zunächst läuft die Biegebemessung wie gewohnt ab. Als bezogenes Moment wird das verwendet, bei dem die angestrebte bezogene Druckzonenhöhe erreicht wird (z.B <math>\mu_{Eds}=0,296</math> für x/d=0,45). | ||
| + | |||
| + | Mithilfe des bezogenen Moments kann das aufnehmbare Moment der so ermittelten Zugbewehrung berechnet werden. Dieses Moment wird im weiteren als Grenzmoment bezeichnet. | ||
| + | |||
| + | <math>lim\ M_{Eds}=lim\ \mu_{Eds}\cdot b^2\cdot d^2\cdot f_{cd}</math> | ||
| + | |||
| + | <math>A_{s1,lim\ M}=\frac{1}{f_{yd}}\cdot\left(\frac{lim\ M_{Eds}}{z}+N_{Ed}\right)</math> | ||
| + | |||
| + | Die Differenz zwischen Gesamtmoment und Grenzmoment muss durch weitere Zugbewehrung und Druckbewehrung aufgenommen werden. | ||
| + | |||
| + | <math>\Delta M_{Eds}=M_{Eds}-lim\ M_{Eds}</math> | ||
| + | |||
| + | Da dieser Momentenanteil nur durch die Druckbewehrung und die zusätzliche Zugbewehrung aufgenommen wird, liegen für diesen Momentenanteil wieder lineare Dehnungsverhältnisse vor und die erforderliche Bewehrung lässt sich mithilfe der folgenden Gleichung ermitteln. | ||
| + | |||
| + | <math>A_{s1,\Delta M}=\frac{1}{f_{yd}}\cdot\left(\frac{\Delta M_{Eds}}{d-d_2}\right)</math> | ||
| + | |||
| + | <math>A_{s2}=\frac{1}{\sigma_{s2}}\cdot\left(\frac{\Delta M_{Eds}}{d-d_2}\right)</math> | ||
| + | |||
| + | Die gesamte Querschnittsfläche der Zugbewehrung ergibt sich durch die Addition beider Anteile, die Querschnittsfläche der Druckbewehrung entspricht der für den zweiten Momentenanteil. | ||
| + | |||
| + | <math>A_{s1}=A_{s1,lim\ M}+A_{s1,\Delta M}</math> | ||
| + | |||
| + | Um ein frühzeitiges Ausknicken der Druckbewehrung zu vermeiden, ist diese ausreichend zu umbüglen (vgl. DIN EN 1992-1-1 9.1.2.1<ref name = "Q4"></ref>). In der Regel ist durch die ohnehin erforderliche Druckbewehrung eine ausreichende Umbügelung gegeben. | ||
| + | |||
| + | ==Plattenbalken== | ||
| + | <p> | ||
| + | Da bei Plattenbalken nur die stegnahen Bereiche vollständig mitwirken und sich die Platte mit zunehmendem Abstand zum Steg der aufgezwungenen Verformung entzieht, wurde die <a href="https://baustatik-wiki.fiw.hs-wismar.de" target="_blank">mitwirkende Plattenbreite</a>. eingeführt. In diesem Bereich wird die komplexe Form der Druckverteilung zu einer mit konstantem Verlauf vereinfacht. | ||
| + | </p> | ||
| + | Bei der Bemessung von Plattenbalken können abhängig von der Lage der Spannungsnulllinie unterschiedliche Fälle unterschieden werden. | ||
| + | |||
| + | Ist die Druckzonenhöhe kleiner als die Höhe der Platte befindet sich die gesamte Druckzone in der Platte und ist somit rechteckförmig. Die Bemessung kann wie für Rechteckquerschnitte durchgeführt werden, als Querschnittsbreite ist die mitwirkende Plattenbreite anzusetzen. | ||
| + | |||
| + | Übersteigt die Druckzonenhöhe die Plattenhöhe, ist die Druckzone nicht mehr rechteckförmig. Dies muss in der Bemessung berücksichtigt werden. Für diesen Fall stehen gesonderte Bemessungshilfsmittel zur Verfügung. | ||
| + | |||
| + | In Bereichen mit negativen Momenten befindet sich die Druckzone im Steg. Es ergibt sich eine rechteckförmige Druckzone, die Bemessung kann wie für Rechteckquerschnitte durchgeführt werden, als Querschnittsbreite ist die Stegbreite anzusetzen. Wenn bezogene Druckzonenhöhe wie von der Norm gefordert auf 0,45 begrenzt wird, kann der Vergleich der Steghöhe mit der Druckzonenhöhe entfallen, da Steghöhe in der Regel größer als die Plattenhöhe ist und dadurch von vornherein davon ausgegangen werden kann, dass die Druckzone rechteckförmig ist. | ||
| − | |||
| − | |||
[[Datei:Spannung Beton.PNG]] | [[Datei:Spannung Beton.PNG]] | ||
[[Datei:Spannung Stahl.PNG]] | [[Datei:Spannung Stahl.PNG]] | ||
Version vom 10. April 2024, 21:21 Uhr
Ziel der Bemessung bzw. des Nachweises eines überwiegend beanspruchten Bauteils ist nachzuweisen, dass der Querschnitt die äußeren Schnittgrößen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed}}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Ed}}
) im Grenzzustand der Tragfähigkeit aufnehmen kann. Bei der Bemessung wird das aufnehmbare Moment durch die Veränderung der Bewehrungsquerschnittsfläche an die vorhandenen äußeren Schnittgrößen angepasst. Beim Nachweis eines biegebeanspruchten Bauteils wird für eine gegebene Bewehrung überprüft, ob die aufnehmbaren Schnittgrößen die einwirkenden Schnittgrößen übersteigt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed}\leq M_{Rd} \qquad\qquad N_{Ed}\leq N_{Rd} }
Tragverhalten
Dehnungsbereiche
Beeinflusst wird die Tragfähigkeit von Biegebauteilen durch die Festigkeiten von Stahl und Beton sowie durch die Querschnittswerte (Breite, Höhe und Form der Druckzone, statische Nutzhöhe, Bewehrungsquerschnittsfläche).
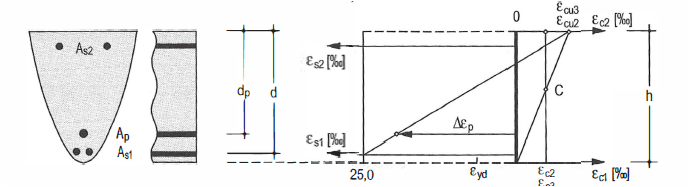
Die Bemessung im Grenzzustand setzt voraus, dass die Bruchdehnung der Bewehrung oder des Betons überschritten wird und dementsprechend ein Stahl- oder Betonversagen eintritt (vgl. Bild… und Bild …). Abhängig von der Beton- und Stahldehnung können dabei fünf Dehnungsbereiche unterschieden werden[1]:
- Dehnungsbereiche 1:
Im gesamten treten ausschließlich Zugdehnungen auf. Die Bewehrung erreicht ihre Bruchdehnung von 25‰, das Versagen findet durch das Versagen der Bewehrung statt. Da vor dem Versagen die Fließgrenze überschritten wird, findet eine Ankündigung des Versagens durch breite Risse statt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_o>0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_u>0 }
wobei:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_o } … untere Randspannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_u } … obere Randspannung
- Dehnungsbereiche 2:
Die Grenzdehnung der Zugbewehrung wird erreicht, in der Druckzone sind noch Tragreserven vorhanden. Das Versagen findet durch Versagen der Zugbewehrung mit Vorankündigung statt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{s1}=\varepsilon_{su} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0>\varepsilon_c>\varepsilon_{c2u} } - Dehnungsbereiche 3:
Die Fließgrenze des Stahls wird überschritten, die Bruchdehnung der Bewehrung wird aber nicht erreicht. Die Bruchdehnung der Betondruckzone wird erreicht. Das Versagen findet durch das Versagen der Betondruckzone statt. Trotz des Betonversagens findet eine Versagensankündigung statt, da der Stahl vor dem Bruch plastizieren kann.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{su}>\varepsilon_{s1}>\varepsilon_{y} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_c=\varepsilon_{c2u} } - Dehnungsbereiche 4:
Der Stahl erreicht die Fließgrenze nicht, die Bruchdehnung des Betons wir überschritten. Die maßgebende Versagensart ist das Betonversagen, da die Stahldehnung unter der Fließgrenze bleibt, findet keine Vorankündigung des Versagens statt. Da wegen der geringen Stahldehnung nicht die volle Zugfestigkeit des Stahls aktiviert wird, ergibt die Bemessung in diesem Bereich große, unwirtschaftliche Bewehrungsquerschnittsflächen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{y}>\varepsilon_{s1}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_c=\varepsilon_{c2u} } - Dehnungsbereiche 5:
Im gesamten Querschnitt treten nur Druckbeanspruchungen auf. Das Versagen findet durch Versagen des Betons ohne Vorankündigung statt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_o<0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_u<0 }
Für überwiegend biegebeanspruchte Bauteile sind die Dehnungsbereiche 2 bis 4 relevant. Querschnitt im Dehnungsbereich 1 und 5 sind überwiegend längskraftbeansprucht. Bei der Bemessung ist stets ein Versagen mit Vorankündigung anzustreben, die Querschnitte sollten sich dementsprechend in den Dehnungsbereichen 2 oder 3 befinden.
Spannungsdehnungslinie
Unter der Voraussetzung, dass sich der Querschnitt in einem der Dehnungsbereiche 1 bis 3 befindet, kann die Spannungs-Dehnungs-Linie von biegebeanspruchten Stahlbetonbauteilen wie auch die für solche unter Zugbeanspruchung in verschiedene Bereiche bzw. Zustände eingeteilt werden:
- Zustand I: In diesem Zustand ist der Beton noch ungerissen, die Betonzugfestigkeit wurde noch in keinem Punkt überschritten, er endet mit der erstmaligen Überschreitung der Betonzugfestigkeit und somit mit der Entstehung des Erstrisses. Im Zustand I spielt die Bewehrung, wegen der geringen Dehnung, welche auch nur eine geringe Zugfestigkeit bewirkt, noch keine Rolle. Das Elastizitätsmodul entspricht dem des Betons.
- Zustand IIa: Dies ist der Bereich, in dem die Rissbildung stattfindet. Er endet, wenn die Rissabstände so gering sind, dass die Zugfestigkeit des Betons zwischen den Rissen nicht mehr überschritten wird. In der Zugzone des Rissquerschnitts beteiligt sich der Beton nicht mehr am Lastabtrag. Die Rissbildung ist mit einem Steifigkeitsabfall verbunden.
- Zustand IIb: Die Rissbildung ist abgeschlossen, bei zunehmender Stahlspannung treten keine neuen Risse mehr auf. Die mit der zunehmenden Stahlspannung verbundenen Stahldehnungen führen zu einer Verbreiterung der vorhandenen Risse. Zustand II a endet, wenn die Fließgrenze erreicht wird.
- Zustand III: Der Stahl beginnt nach der Überschreitung der Fließgrenze zu plastizieren. Es findet noch eine leichte Steigerung der Stahlspannungen statt. Zustand III endet mit dem Versagen der Bewehrung oder der Betondruckzone.
Befindet sich der Querschnitt im Dehnungsbereich 4 gelten die gleichen Beziehungen abgesehen davon, dass Zustand III entfällt, da vor der Erreichung der Fließgrenze des Stahls das Betonversagen stattfindet.
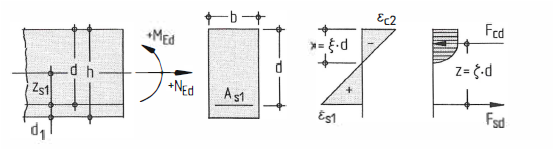
Im Zustand I sind die Spannungen noch linear über den Querschnitt verteilt (vgl. Bild…), eine geschlossene Ermittlung der inneren Schnittgrößen ist daher möglich. Im Zustand II und III sind die Spannungen nicht mehr linear über den Querschnitt verteilt; in der Zugzone wird die Betonspannung null, da die Bemessung im Rissquerschnitt stattfindet. Außerdem wird die Spannungs-Dehnungs-Linie des Betons wegen der höheren Dehnungen nichtlinear[2].
Sicherstellung der Duktilität
Um eine ausreichende Versagensankündigung zu garantieren, ist sicherzustellen, dass die bei der Rissbildung freiwerdenden Zugkräfte durch die Zugbewehrung ohne schlagartiges Versagen aufgenommen werden können. Dies wird durch die Anordnung einer Mindestbewehrung sichergestellt.
Außerdem ist sicherzustellen, dass die Stahldehnung zum Versagenszeitpunkt über der Fließgrenze liegt. Hierfür ist die Druckzonenhöhe zu begrenzen. Wenn die Betonstauchung am oberen Rand der Bruchstauchung des Betons entspricht, findet eine Erhöhung der aufnehmbaren Betondruckkraft nur noch durch die Vergrößerung der Druckzone statt[2], hierdurch sinkt der Hebelarm der inneren Kräfte. Aufgrund der linearen Dehnungsverteilung über die Querschnittshöhe nimmt außerdem mit steigender Druckzonenhöhe x die Dehnung der Zugbewehrung ab. Wenn die Stahldehnung der Zugbewehrung dabei unter die Fließgrenze fällt, kommt es zu unwirtschaftlichen Bemessungsergebnissen und zu einem Versagen ohne Vorankündigung.
Der theoretische Wert der bezogenen Druckzonenhöhe, bei dem die Dehnung der Zugbewehrung die Fließgrenze noch geradeso erreicht, beträgt x/d=0,617. Gemäß DIN EN 1992-1-1/NA 5.4[3] sollte x/d für normalfeste Beton kleiner als 0,45 und für hochfeste Betone kleiner als 0,35 sein.
Um die bezogene Druckzonenhöhe zu begrenzen, gibt es zwei Möglichkeiten. Die erste Möglichkeit ist eine Verbreiterung der Druckzone (vgl. Plattenbalken), die zweite die Anordnung einer Druckbewehrung (vgl. Druckbewehrung).
Bemessung
Die Biegebemessung erfolgt für Bauteile im Zustand II im Rissquerschnitt. Eine geschlossene Lösung ist wegen der Nichtlinearität im Zustand II nicht mehr möglich. Aus demselben Grund ist auch die getrennte Bemessung für Normalkraft und Momente ausgeschlossen, da die Superposition der Auswirkung beider Lastfälle nicht mehr möglich ist[2].
Vorbemessung
äußere Schnittgrößen
In der Regel ist es sinnvoll die äußeren Schnittgrößen auf die Schwerelinie der Bewehrung zu beziehen. Verschiebt man die Normalkraft für die Bemessung auf die Schwerelinie der Bewehrung, ist dies auch beim einwirkdenden Moment zu berücksichtigen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Eds}=M_{Ed}-N_{Ed}\cdot z_{s1} }
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_{s1} } … Abstand der Schwerelinie der Zugbewehrung zur Schwerelinie des Querschnitts
Grundsätzliche Annahmen
Die folgenden Voraussetzungen werden der Biegebemessung zugrunde gelegt[4]:
- Die Hypothese von Bernoulli gilt, d.h. dass die angenommen wird, dass die Dehnungen linear über den Querschnitt verteilt sind (Ebenbleiben der Querschnitte). Diese Annahme gilt für schlanke ist für schlanke Bauteile erfüllt (l/h$\geq$2 bzw. für Kragträger $l_k\geq1$), nicht erfüllt ist sie in Bereichen mit konzentrierter Lasteinleitung (z. B. unter Einzellasten oder im Auflagerbereich). Für Bereiche in denen nicht davon ausgegangen werden kann, dass die Dehnungen linear über den Querschnitt verteilt sind, müssen andere Bemessungsverfahren verwendet werden z.B. Stabwerkmodelle.
- Die Zugfestigkeit des Betons wird in der Bemessung nicht angesetzt, die Bemessung erfolgt im Rissquerschnitt.
- Zwischen der Bewehrung und dem Beton wird starrer Verbund vorausgesetzt, d.h. die Dehnung der Bewehrung entspricht der der angrenzenden Betonfaser.
- Für die Spannungsdehnungslinie des Betons und der Bewehrung gelten die Zusammenhänge aus Bild … und Bild ….
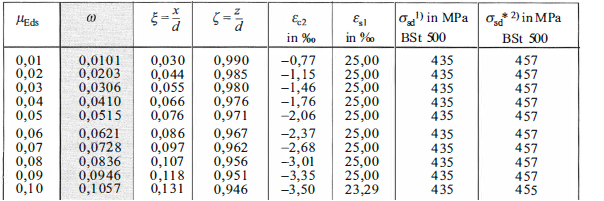
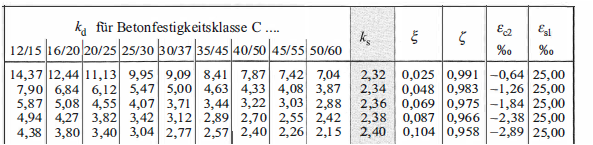
Die Ermittlung des Bauteilwiderstands erfolgt durch Variation der Dehnungsebenen, bis sich innere und äußere Schnittgrößen im Gleichgewicht befinden. Da dies ein iterativer Prozess ist, der bei einer Handrechnung einen hohen Aufwand bedeutet, werden i.d.R Bemessungshilfsmittel verwendet, diese können gängigen Tabellenwerekn z.B. Schneider Bautabellen[5] entnommen werden. Für die Erstellung von Bemessungshilfsmitteln bietet sich die Verwendung von dimensionslosen Beiwerten an.
Im Folgenden werden das allgemeine Bemessungsdiagramm, das $\omega$-Verfahren und das $k_d$-Verfahren. Anschließend findet auch noch eine Herleitung der Gleichungen für die Biegebemessung mit einem parabel-rechteckförmigen Spannungsverlauf in der Druckzone (iterative Lösung) und mit dem vereinfachten rechteckförmigen Spannungsblock (geschlossene Lösung) statt.
Druckbewehrung
Durch die Anordnung einer Druckbewehrung wird die Betondruckzone entlastet und die Druckzonenhöhe reduziert bzw. nicht mehr gesteigert. In der Regel kann bei der Bemessung trotz der Druckbewehrung mit der Bruttofläche der Betondruckzone gerechnet werden, da die Unterschiede im Vergleich zur Bemessung mit der Nettofläche gering sind[2].
Für Rechteckquerschnitte mit Druckbewehrung stehen ebenfalls Bemessungshilfsmittel zur Verfügung[5]. Es können auch die Bemessungshilfsmittel für Rechteckquerschnitte ohne Druckbewehrung verwendet werden, dabei ist dann das einwirkende Moment aufzuteilen (vgl. Bild …).
Zunächst läuft die Biegebemessung wie gewohnt ab. Als bezogenes Moment wird das verwendet, bei dem die angestrebte bezogene Druckzonenhöhe erreicht wird (z.B Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}=0,296} für x/d=0,45).
Mithilfe des bezogenen Moments kann das aufnehmbare Moment der so ermittelten Zugbewehrung berechnet werden. Dieses Moment wird im weiteren als Grenzmoment bezeichnet.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle lim\ M_{Eds}=lim\ \mu_{Eds}\cdot b^2\cdot d^2\cdot f_{cd}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s1,lim\ M}=\frac{1}{f_{yd}}\cdot\left(\frac{lim\ M_{Eds}}{z}+N_{Ed}\right)}
Die Differenz zwischen Gesamtmoment und Grenzmoment muss durch weitere Zugbewehrung und Druckbewehrung aufgenommen werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta M_{Eds}=M_{Eds}-lim\ M_{Eds}}
Da dieser Momentenanteil nur durch die Druckbewehrung und die zusätzliche Zugbewehrung aufgenommen wird, liegen für diesen Momentenanteil wieder lineare Dehnungsverhältnisse vor und die erforderliche Bewehrung lässt sich mithilfe der folgenden Gleichung ermitteln.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s1,\Delta M}=\frac{1}{f_{yd}}\cdot\left(\frac{\Delta M_{Eds}}{d-d_2}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s2}=\frac{1}{\sigma_{s2}}\cdot\left(\frac{\Delta M_{Eds}}{d-d_2}\right)}
Die gesamte Querschnittsfläche der Zugbewehrung ergibt sich durch die Addition beider Anteile, die Querschnittsfläche der Druckbewehrung entspricht der für den zweiten Momentenanteil.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s1}=A_{s1,lim\ M}+A_{s1,\Delta M}}
Um ein frühzeitiges Ausknicken der Druckbewehrung zu vermeiden, ist diese ausreichend zu umbüglen (vgl. DIN EN 1992-1-1 9.1.2.1[5]). In der Regel ist durch die ohnehin erforderliche Druckbewehrung eine ausreichende Umbügelung gegeben.
Plattenbalken
Da bei Plattenbalken nur die stegnahen Bereiche vollständig mitwirken und sich die Platte mit zunehmendem Abstand zum Steg der aufgezwungenen Verformung entzieht, wurde die <a href="https://baustatik-wiki.fiw.hs-wismar.de" target="_blank">mitwirkende Plattenbreite</a>. eingeführt. In diesem Bereich wird die komplexe Form der Druckverteilung zu einer mit konstantem Verlauf vereinfacht.
Bei der Bemessung von Plattenbalken können abhängig von der Lage der Spannungsnulllinie unterschiedliche Fälle unterschieden werden.
Ist die Druckzonenhöhe kleiner als die Höhe der Platte befindet sich die gesamte Druckzone in der Platte und ist somit rechteckförmig. Die Bemessung kann wie für Rechteckquerschnitte durchgeführt werden, als Querschnittsbreite ist die mitwirkende Plattenbreite anzusetzen.
Übersteigt die Druckzonenhöhe die Plattenhöhe, ist die Druckzone nicht mehr rechteckförmig. Dies muss in der Bemessung berücksichtigt werden. Für diesen Fall stehen gesonderte Bemessungshilfsmittel zur Verfügung.
In Bereichen mit negativen Momenten befindet sich die Druckzone im Steg. Es ergibt sich eine rechteckförmige Druckzone, die Bemessung kann wie für Rechteckquerschnitte durchgeführt werden, als Querschnittsbreite ist die Stegbreite anzusetzen. Wenn bezogene Druckzonenhöhe wie von der Norm gefordert auf 0,45 begrenzt wird, kann der Vergleich der Steghöhe mit der Druckzonenhöhe entfallen, da Steghöhe in der Regel größer als die Plattenhöhe ist und dadurch von vornherein davon ausgegangen werden kann, dass die Druckzone rechteckförmig ist.
Quellen
- ↑ Wommelsdorff,O., Albert,A., Fischer,J., Stahlbetonbau-Bemessung und Konstruktion Teil 1, 11. Auflage, Köln: Bundesanzeiger Verlag, 2017
- ↑ 2,0 2,1 2,2 2,3 Zilch,K., Zehetmaier,G., Bemessung im konstruktiven Betonbau, 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006
- ↑ DIN EN 1992-1-1/NA, Nationaler Anhang - National festgelegte Parameter - Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2013
- ↑ DIN EN 1992-1-1, Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2011
- ↑ 5,0 5,1 5,2 Albert,A., Bautabellen fü Ingenieure, Auflage 26, Bundesanzeigerverlag, 2024
Seiteninfo
|