Heißbemessung

Einleitung

Neben den Grenzzuständen der Tragfähigkeit und der Gebrauchstauglichkeit, welche die alltäglichen Anforderungen unter normalen Bedingungen an Gebäuden wiederspiegeln, müssen auch außergewöhnliche Bemessungssituationen betrachtet werden. Eine von diesen Situationen ist die Bemessung von tragenden Bauteilen für den Brandfall. Der Grund einer „heißen Bemessung“ ist es, dass für eine geforderte Branddauer die Standsicherheit eines Gebäudes sichergestellt werden muss. Zum einen um den Nutzer des Objektes ausreichend Zeit zu verschaffen das Gebäude im Brandfall zu verlassen. Zum anderen um den Rettungskräften die Möglichkeit zu geben, das Gebäude zu betreten und die Hilfemaßnahmen einzuleiten, ohne selbst gefährdet zu werden.

Grundlagen der Heißbemessung

Brandverlauf

Um eine Heißbemessung zu verstehen, muss man den Ablauf eines Brandes nachvollziehen können. Naturbrände können grob in drei Phasen unterteilt werden.

Zündungs- und Entstehungsphase: Der Brand entsteht durch Entzündung brennbarer Stoffe. Wenn diese in ausreichender Form vorhanden sind, kann sich der Brand ausbreiten. Ist dies nicht der Fall, verlöscht das Feuer bevor es auf andere Materialien übergreifen kann. Die entzündeten Materialien setzen Energie frei und das Feuer breitet sich auf andere Stoffe aus. Dabei steigt die Temperatur stetig an. Außerdem werden Gase freigesetzt, die eine zündfähige Atmosphäre bilden.

Flashover und Vollbrand: Wenn eine bestimmte Temperatur erreicht ist, zündet das Gasgemisch schlagartig durch (Flashover) wobei die Temperatur stark ansteigt. Nun steht der Raum im Vollbrand. Diese Phase hält solange an wie Material und Sauerstoff vorhanden sind, wobei die Temperatur nahezu konstant bleibt.

Abklingende Phase: Das entzündete Material verbrennt und die Temperaturen fallen ab, bis der Brand verlöscht. Wie schnell der Temperaturabfall voranschreitet hängt von der Beschaffenheit des Raumes ab, sowie von dem Wärmespeichervermögen der Materialien.

Brandmodelle

Um Bauteile allgemein bemessen zu können, wurden verschiedene Brandmodelle entwickelt. Das sind zum einen die Naturbrandmodelle und zum anderen die Normbrandmodelle. Die verschiedenen Modelle basieren auf den Ablauf eines normalen Brandes, werden aber unterschiedlich idealisiert.

Naturbrandmodelle

Naturbrandmodelle bilden einen realistischen Brand nach, indem die Temperaturentwicklung eines natürlichen Brandverlaufes berücksichtigt wird. Das bedeutet, dass jedens Naturbrandmodell eine nutzungsspezifische Brandlast besitzt. Die Temperaturbeanspruchung im Verlauf des Brandes nimmt in dem Maße ab, in dem die Brandlast verbraucht wird. So entsteht ein realistisches Bild eines Brandesm auf dessen Grundlage die Buteile bemessen werden können. Im Gegensatz zur Einheitstemperaturkurve können bei langen Branddauern aufgrund der sinkenden Hitze im Verlauf des Brandes wirtschaftlichere Ergebnisse erzielt werden. Das sind zum Beispiel gringere erforderliche Feuerwiderstände bei Türen und anderen Bauteilen.
Die folgenden Naturbrandmodelle werden genannt, in den Klammern "()" sind die angegebenen informativen Anhänge geregelt:

1. Vereinfachte Brandmodelle

• für Vollbrände
  • Beschreibung auf der Grundlage physikalischer Parameter
  • für innenliegende Bauteile (in Anhang A geregelt) zu bzw.
  • für außenliegende Bauteile ( in Anhang B geregelt)
• für lokale Brände
  • Beschreibung mit Hilfe von Plume-Modell (in Anhang C geregelt)

2. allgemeine Brandmodelle (in Anhang D geregelt)

• Das Ein-Zonen-Modell
• Das Zwei-Zonen-Modell
• Feldmodell

Hinweis : Im nationalen Anhang wird zum Naturbrandmodell folgendes geregelt: "Naturbrandmodelle nach 3.3.1 bzw. 3.3.2 sollten nur im Zusammenhang mit einem Brandschutzkonzept bzw. Brandschutznachweis (nach Landesrecht) angewendet werden." Im Nationalen Anhang wird die Anwendbarkeit des vereinfachten Naturbrandmodell teilweise eingeschränkt bzw. abweichend geregelt. Des Weiteren ist in Anhang BB die Vorgaben zur Ermittlung der Brandeinwirkung mit Naturbrandmodell neu geregelt.

Normbrandmodelle

Bei Normbrandmodellen werden Brandverläufe idealisiert. Somit ergeben sich Temperaturzeitkurven, die auf der sicheren Seite liegen und als Bemessungsgrundlage für die Heißbemessung im Eurocode dienen. Diese Brandkuven können bei großen Brandfällen zu sehr unwirtschaftlichen Ergebnissenführen. Hier ist es hilfreich auf Naturbrandmodelle zurückzugreifen. Für Standartnachweise ist die ETK zu verwenden.
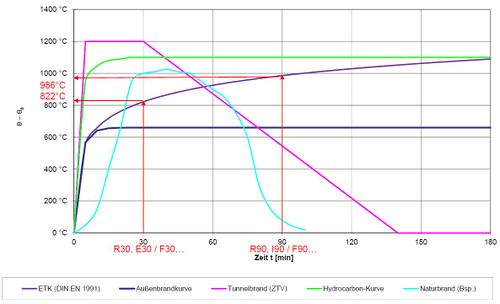
Im Eurocode wird zwischen drei Temperaturzeitkurven unterschieden.

• Hydrokarbonkurve

Bei der Betrachtung der Hydrokarbonkurve fällt auf, dass nach relativ kurzer Zeit ein enormer Temperaturanstieg zu verzeichnen und nach wenigen Minuten eine Temperatur von 1100 °C erreicht ist. Diese Kurve wird bei Bemessungsbränden herangezogen, indem nach kurzer Zeit extrem hohe Temperaturen entstehen, zum Beispiel bei Tunnelbränden oder bei Flüssigkeitsbränden.

• Einheits-Temperaturzeitkurve (ETK)

Bei der ETK steigt die Temperatur allmählich an und nach ca. 180 min sind auch hier die 1100 °C erreicht. Alle Tabellen, die in der alten Brandschutznorm oder in den Eurocode erstellt wurden, sind anhand der Einheitstemperaturzeitkurve geprüft.

In der Regel ist die Einheitstemperaturzeitkurve für brandschutztechnische Nachweise von Tragwerken im Hochbau anzuwenden.

• Externe Brandkurve

Die "Externe Brandkurve" oder auch "Außenbrandkurve" genannt, kann unter bestimmten Randbedingungen, z.B. bei Bauteilen bzw. Bauteiloberflächen die, außerhalb des Brandherdes liegen, verwendet werden.

Brandkurven für Normbrände und Naturbrände im Vergleich

Brandkurven nach Bauordnungsrecht und Naturbrände

Mechamische Einwirkungen

Im EC1-1-2 wird im Brandfall anzunehmenden mechanischen Einwirkungen in direkte und indirekte Einwirkungen unterschieden.

Indirekte Einwirkungen

Indirekte Einwirkungen infolge Brandbeanspruchung sind Kräfte und Momente, die durch thermische Ausdehnungen, Verformungen und Verkrümmungen hervorgerufen werden. Sie müssen nicht berücksichtigt werden, wenn sie das Tragverhalten nur geringfügig beeinflussen und/oder durch entsprechende Ausbildung der Auflager aufgenommen werden können. Außerdem brauchen sie bei der brandschutztechnischen Bemessung von Einzelbauteilen nicht gesondert verfolgt werden. Wenn indirekte Einwirkungen berücksichtigt werden müssen, sind sie unter Ansatz der thermischen und mechanischen Materialkennwerte aus den baustoffbezogenen Eurocodes zu ermitteln.

Direkte Einwirkungen

Als direkte Einwirkungen werden die bei der Bemessung für Normaltemperatur berücksichtigten Lasten (Eigengewicht, Wind, Schnee usw.) bezeichnet. Die maßgebenden Werte der Einwirkungen sind den verschiedenen Teilen der DIN EN 1991 bzw. den zugehörigen nationalen Anhängen zu entnehmen, wo auch allgemeine Regeln zur Berücksichtigung von Schnee- und Windlasten sowie Lasten infolge des Betriebes (z. B. Horizontalkräfte infolge Kranbewegung) angegeben werden. Eine Verringerung der Belastung durch Abbrand bleibt unberücksichtigt.

Allgemeine Regeln

Für die Einwirkungen gilt die DIN EN1991-1-1/2. Es werden die charakteristischen Lasten wie für die kalte Bemessung angesetzt. Die Einwirkungen im Brandfall Efi,d,t ergeben sich nach den Kombinationsregeln in DIN EN 1990 zu:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_{fi,d}=\sum\gamma_{G}\cdot{E_{Gk}}\oplus\gamma_{Q,1}\cdot{\psi_{1,1}}\cdot{E_{Qk,1}}\oplus\sum\gamma_{Q,i}\cdot{\psi_{2,i}}\cdot{E_{Qk,i}}\oplus\sum{{A_{d}(t)}}}

mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{fi,d}}} - der Bemessungseinwirkung im Brandfalls
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{G}_{k}}} - der ständigen, charakteristische Einwirkungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{Q}_{k,1}}} - der veränderlichen, charakteristischen Leiteinwirkung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{Q}_{k,i}}} - der der veränderlichen, charakteristische Einwirkungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{d}}(t)} - Bemessungswert der indirekten Einwirkungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_{i}} - Teilsicherheitsbeiwert der Einwirkung nach DIN EN1990
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi_{i}} - Kombinationsbeiwert der Einwirkun nach DIN EN1990

Hinweis : Nach DIN EN1992-1-2 NA gelten folgende Erleichterungen für den Kombinationsbeiwert der Leiteinwirkung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi_{1,1}} : Es darf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi_{1,1}} durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi_{2,1}} ersetzt werden. Jedoch nur, wenn die Leiteinwirkung nicht der Wind ist.

Vereinfachte Regeln

Wenn indirekte Einwirkungen - also solche, die aus Verformungen im Brandfall resultieren - vernachlässigbar klein sind, gilt vereinfachend die außergewöhnliche Einwirkungskombination als über den Brandverlauf konstant:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{fi,d,t}}=E{}_{fi,d}~}

mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{fi,d,t}}} - der außergewöhnlichen Kombination für den Brandfall (mit den Indizes fire, design, time)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E{}_{fi,d}} - der außergewöhnlichen Kombination über den Brandfall konstant

Die Einwirkung während des Brandes kann mittels Reduktionsfaktor aus der Einwirkung unter Normaltemperatur ermittelt werden:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{fi,d}}={{E}_{d}}\cdot {{\eta }_{fi}}}

mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{fi,d}}} - der Bemessungseinwirkung während des Brandfalls
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{d}}} - der Bemessungseinwirkung bei Normaltemperatur
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\eta }_{fi}}} - dem Reduktionsfaktor.

Hinweis : Der Reduktionsfaktor kann vereinfachend und auf der sicheren Seite mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \eta_{fi}=0,7} angenommen werden.

Der Reduktionsfaktor lässt sich folgendermaßen ermitteln:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\eta }_{fi}}=\frac{{{G}_{k}}+{{\psi }_{fi}}\cdot {{Q}_{k,1}}}{{{\gamma }_{G}}\cdot {{G}_{k}}+{{\gamma }_{Q,1}}\cdot {{Q}_{k,1}}}}

mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{G}_{k}}} - der ständigen, charakteristische Einwirkungen (mit Index charakteristisch)
${{Q}_{k,1}}$ - der veränderlichen, charakteristische Leiteinwirkung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{G}}} - dem Teilsicherheitsbeiwert für ständige Einwirkungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{Q,1}}} - dem Teilsicherheitsbeiwert für veränderliche Leiteinwirkung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\psi }_{fi}}} - dem Kombinationsfaktor für den Brandfall als außergewöhnliche Situation, entspricht ψ2 (quasi-ständig) oder im Ausnahmefall Wind ψ1 (häufig).

Beispielrechnung

Lasten im Brandfall (Bsp.)

Thermische Einwirkungen

Die thermischen Einwirkungen auf Bauteile werden in Abhängigkeit von der (Heißgas-) Temperatur θ_g in der Bauteilumgebung als Netto-Wärmestrom ḣ_net vorgegeben, der aus einem konvektiven Anteil und einem radiativen Anteil besteht:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\overset{\centerdot }{\mathop{h}}\,}_{net}}= {\color{red}{\overset{\centerdot }{\mathop{h}}\,}_{net,c}}+ {\color{OliveGreen}{\overset{\centerdot }{\mathop{h}}\,}_{net,r}} }

(1.1)

Dabei ist ḣ_net,c gegeben durch Gleichung (1.2) und ḣ_net,r durch Gleichung (1.3).

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\color{red}{\overset{\centerdot }{\mathop{h}}\,}_{net,c}}= {{\alpha }_{c}}\cdot ({{\theta }_{g}}-{{\theta }_{m}}) }

(1.2)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{c}}}

der Wärmeübergangskoeffizient für Konvektion [W/m²K]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\theta }_{g}}}

die Gastemperatur in der Umgebung des beanspruchten Bauteils [°C]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\theta }_{m}}}

die Oberflächentemperatur des Bauteils [°C]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\color{OliveGreen}{\overset{\centerdot }{\mathop{h}}\,}_{net,r}}= \phi \cdot {{\varepsilon }_{m}}\cdot {{\varepsilon }_{f}}\cdot \sigma \cdot \left[ {{({{\theta }_{r}}+273)}^{4}}-{{({{\theta}_{m}}+273)}^{4}} \right] }

(1.3)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi}

Konfigurationsfaktor (zur Berücksichtigung von Abschattungen) [-]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{m}}}

Emissivität der Bauteiloberfläche [-] [°C]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{f}}}

Emissivität des Feuers [-]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma }

Stefan Boltzmann Konstante Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left( \text{=5}\text{,67}\cdot \text{1}{{\text{0}}^{\text{-8}}} \right)} [W/m²K4]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\theta }_{r}}}

Strahlungstemperatur der Umgebung [°C]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\theta }_{m}}}

Oberflächentemperatur des Bauteils [°C]

Hinweis : Vereinfachend und auf der sicheren Seite liegend kann der Konfigurationsfaktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi \text{=1}\text{,0}} gesetzt werden und die Strahlungstemperatur θr entspricht gleich der Heißgastemperatur θg.

Die Werte, die für den Wärmeübergangskoeffizient für Konvektion angesetzt werden, valieren je nach Brandkurve und nach Lage der Bauteiloberflächen zum Brandherd, somit darf für die feuerabgekehrten Bauteilseite mit α_c = 4 W/m2K angenommen werden. Mit α_c = 9 W/m2K kann gerechnet werden, wenn die Wärmeübertragung durch Strahlung mit abgedeckt werden soll. (Siehe Tabelle) Falls in den baustoffbezogenen Eurocodes keine anderen Angaben gemacht werden, darf ε_m = 0,8 gesetzt werden; für die Emissivität der Flamme gilt im Allgemeinen ε_f = 1,0. Für die brandschutztechnische Bemessung werden verschiedene nominelle Temperaturzeitkurven zur Beschreibung der Heißgastemperatur θg in Abhängigkeit der Branddauer t [min] mit dem jeweils zugehörigen Wärmeübergangskoeffizienten für Konvektion α_c vorgegeben.

Wärmeübergangszahlen für Konvektion nach Eurocode 1

Brand abgewandte Seite von trennenden Bauteilen	αc [W/m²K]
Möglichkeit 1: Wärmeübergang durch Strahlung wird gesondert berücksichtigt	4
Möglichkeit 2: Wärmeübergang durch Strahlung ist enthalten	9
Brand zugewandte Seite der Bauteiloberfläche:
Einheitstemperaturzeitkurve oder externe Brandkurve	25
Hydrocarbon-Brandkurve	50
Parametrische Brände, Zonenmodelle oder außenliegende Bauteile	35

Heißbemessung nach Eurocode (EC)

Die Heißbemessung wird in allen Bauarten, die nach Eurocode verwendet werden, durchgeführt und berücksichtigen die speziellen Eigenschaften der verwendeten Baustoffe.

Heißbemessung nach DIN EN1992-1-2: Heißbemessung Stahlbetonbau

Heißbemessung nach DIN EN1993-1-2: Heißbemessung Stahlbau

Isothermen Methode Test

Hinweis : Als Normzitat ist der Text rötlich hinterlegt

B.1 500 °C-Isothermen-Methode B.1.1 Prinzip und Anwendungsgebiet (1) Diese Methode kann bei einer Normbrandbeanspruchung und allen anderen Bauteilerwärmungen, die ähnliche Temperaturfelder im brandbeanspruchten Bauteil verursachen, angewendet werden. Bei Bauteilerwärmungen, die dieses Kriterium nicht erfüllen, muss eine getrennte umfassende Analyse, die die relative Festigkeit des Betons als eine Funktion der Temperatur berücksichtigt, durchgeführt werden. (2) Diese Methode gilt für eine Mindestbreite des in Tabelle B.1 angegebenen Querschnitts: für eine Normbrandbeanspruchung, welche von Feuerwiderstandsklasse abhängig ist; füreine parameterabhängige Brandbeanspruchung mit einem Öffnungsfaktor O ≥ 0,14 m1/2 (siehe EN 1991-1-2, Anhang A). Tabelle B1 - Mindestbreiten des Querscnitts als Funktion der Feuerwiderstandsklasse (bei Normbrandbeanspruchung) sowie Brandlastdichte (bei parameterabhängiger Brandbeanspruchung) a) Feuerwiderstand Feuerwiderstandsklasse R 60 R 90 R 120 R 180 R 240 Mindestbreite der Querschnitts in mm 90 120 160 200 280 b) Brandlastdichte Brandlastdichte MJ/m^2 200 300 400 600 800 Mindestbreite der Querschnitts in mm 100 140 160 200 240 (3) Die vereinfachte Berechnungsmethode umfasst eine (AC)gestrichener Text(AC) Verkleinerung der Querschnittsgröße unter Berücksichtigung eines durch den Brand geschädigten Bereichs nahe der Betonoberfläche. Die Dicke des geschädigten Betons a500 wird der mittleren Tiefe der 500 °C-Isotherme in der Druckzone des Querschnitts gleichgesetzt. (4) Es wird angenommen,(AC)gestrichender Text(AC), d. h. über 500 °C heißer Beton, keinen Beitrag zur Tragfähigkeit des Bauteils leistet, während der restliche Betonquerschnitt seine anfängliche Festigkeit und Elastizitätsmodul beibehält. (5) Bei einem rechteckigen Balken, der von drei Seiten durch einen Brand beansprucht wird, (AC) stimmt der reduzierte Querschnitt im Brandfall mit Bild B.1a) oder B.1b) überein. (AC) B.1.2 Berechnungsverfahren eines durch Biegemoment und Längskraft beanspruchten Stahlbetonquerschnitts (1) Auf der Basis des oben beschriebenen Ansatzes für einen verkleinerten Querschnitt kann das Verfahren zur Berechnung des Widerstandes eines Stahlbetonquerschnitts im Brandfall folgendermaßen durchgeführt werden: Bestimmung der 500 °C-Isotherme für eine bestimmte Brandbeanspruchung, eine Normbrandbeanspruchung oder eine parameterabhängige Brandbeanspruchung; Bestimmung einer neuen Breite bfi und einer neue statischen Nutzhöhe dfi des Querschnitts durch Ausschluss des Betons außerhalb der 500 °C-Isotherme (siehe Bild B.1). Die abgerundeten Ecken der Isothermen können durch ein Rechteck oder Quadrat, wie in Bild B.1 angegeben, angenähert werden; BILD Bestimmung der Temperatur des Stahlbetonbalkens in der Zug- und Druckzone. Die Temperatur in den einzelnen Bewehrungsstäbe kann anhand der Temperaturprofile in Anhang A oder aus Handbüchern ermittelt werden. Einige der Bewehrungsstäbe können, wie in Bild B.1 dargestellt, außerhalb des verkleinerten Querschnitts liegen. Trotzdem können sie in die Berechnung der maximalen Tragfähigkeit des brandbeanspruchten Querschnitts einbezogen werden; Bestimmung der durch die Temperatur reduzierten Festigkeit der Bewehrung nach 4.2.4.3; Verwendung konventioneller Berechnungsmethoden zur Bestimmung der maximalen Tragfähigkeit unter Berücksichtigung des verkleinerten Querschnitts und der Festigkeit der Bewehrungsstäbe wie in d) ermittelt; Vergleich der maximalen Tragfähigkeit mit den Bemessungswerten der Schnittgrößen oder alternativ: Vergleich der berechneten mit der erforderlichen Feuerwiderstandsdauer. (2) Bild B.2 zeigt die Berechnung der Tragfähigkeit eines Querschnitts mit Zug- und Druckbewehrung. BILD (3) Wenn alle Bewehrungsstäbe in Lagen angeordnet sind und dieselbe Querschnittsfläche haben, könnendie folgenden Ausdrücke (AC)bei der Berechnung des Achsabstandes a verwendet werden.(AC) Die mittlere infolge Temperatureinwirkung reduzierte Festigkeit einer Bewehrungslage wird in Überein-stimmung mit Gleichung (B.1) berechnet. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{k}_{v}(\Theta)}=\cfrac{\sum{k(\Theta_i)}}{n_v}\text{ }} (B.1) Dabei ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\Theta}} - die Temperatur eines Bewehrungsstabes i; Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {k(\Theta_i)}} - die Reduktion der Festigkeit des Bewehrungsstabes i aufgrund der Temperatur θi,(AC) die aus Bild 4.1 entnommen wird; (AC) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {kv(\Theta)}} - die durchschnittliche Reduktion der Festigkeit der Bewehrungslage ν; Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n_v}} - die Anzahl der Bewehrungsstäbe in Lage ν; (4) (AC) der Achsabstand a zum Mittelpunkt der Bewehrungslagen kann unter Verwendung von Gleichung (B.2) berechnet werden: (AC) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {a}=\cfrac{\sum{{a_v}{k(\Theta_i)}}}{\sum{k_v(\Theta)}}\text{ }} (B.1) Dabei ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {a_v}} - (AC)der Achsabstand von der unteren Oberfläche des verkleinerten Querschnitts zur Bewehrungslage ν(AC); Quellenangaben