Direkte Verformungsberechnung - biegebeanspruchte Bauteile

Verformung und Durchbiegung von Stahlbetonbauteilen

Allgemeines

Im Rahmen der Nachweise im Grenzzustand der Gebrauchstauglichkeit wird unter anderem der Verformungsnachweis geführt, um die Nutzbarkeit des Bauteils sicherzustellen und Schäden an angrenzenden Bauteilen zu vermeiden.

Die Verformungen von Stahlbetonbauteilen sind maßgeblich von den Steifigkeit abhängig. In dem Verbundwerkstoff Stahlbeton nimmt die Bewehrung die Zugkräfte auf während der Beton die Zugkräfte aufnimmt. Die Zugfestigkeit der Bewehrung ist deutlich höher als die des Betons. Sobald die Zugkräfte in den Randfasern des Betons dessen mittlere Betonzugfestigkeit überschreiten kommt es zur Rissbildung im Beton. Der Rissbildungsprozess geht mit einem Abfall der Steifigkeit einher. Infolge des Steifigkeitsabfalls nehmen die Verformungen zu.

Die Verformungsberechnung von Stahlbetonbauteilen wird dadurch erschwert, dass sich nicht das ganze Bauteil im Zustand I bzw. II befindet, sodass die Steifigkeiten abschnittsweise differieren.

Verformungen im Stahlbetonbau lassen sich in zwei Kategorien unterscheiden:

• Verformungen unter Kurzzeitverhalten
• Verformungen unter Langzeitverhalten

Das Kurzzeitverhalten des Betons beschreibt dabei dessen Materialverhalten wie Betondruckfestigkeit, Betonzugfestigkeit und Elastizitätsmodul und dessen zeitliche Entwicklung. Das Langzeitverhalten des Betons beschreibt dabei dessen Materialverhalten unter den Faktoren von Kriechen und Schwinden des Betons. Schwinden ist dabei ein lastunabhängiger Prozess und resultiert im wesentlichen durch die durch Austrocknung bedingte Verkürzung des Betons; Kriechen ist dabei ein lastabhängiger Prozess und resultiert in einer Dehnung unter konstanter Belastung.

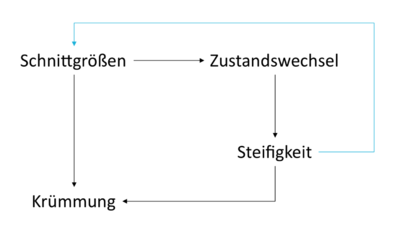
Zusammenhang Belastung - Steifigkeit - Krümmung

Nach den allgemeinen Ansätzen der Mechanik lassen sich die Krümmungen eines Bauteils in Abhängigkeit aus der Belastung und der Steifigkeit des Querschnittes stellen:

$\kappa =(1/r)={\frac {M}{EI}}$

Die Durchbiegung aus der Krümmung ergibt sich dabei nach zweifacher Integration der Krümmung:

$w(x)=\int _{}^{}\int _{}^{}{\frac {M(x)}{EI(x)}}dx$

Die Abhängigkeiten der Durchbiegungen stehen also im Verhältnis der Systemlänge, Belastung und Steifigkeit. Unter Annahme eines zum Krümmungsverlauf affinen Momentenverlaufes lässt sich das Doppelintegral der Krümmung unter zur Hilfenahme des Prinzips der virtuellen Kräfte zu folgendem Ausdruck umstellen:

$w(x)=\int _{}^{}{\frac {{\overline {M}}(x)\cdot M(x)}{EI(x)}}dx=\int _{}^{}({\overline {M}}(x)\cdot \kappa )dx\approx k\cdot \kappa \cdot l^{2}=w(l/2)$

K beschreibt dabei einen Beiwert zur Beachtung des Momentenverlaufs und lässt sich herleiten aus den Integraltafeln oder aus der Literatur direkt entnehmen.

Zustand I, Zustand II und Rissbildung

Tabelle: Formeln zur Ermittlung der Querschnittswerte im Zustand I und II für bewehrte Betonquerschnitte mit Zugbewehrung

Prinzipdarstellung: Vergleich der wirkenden Belastung und des Rissmomentes zur Beurteilung des Zustandwechsels

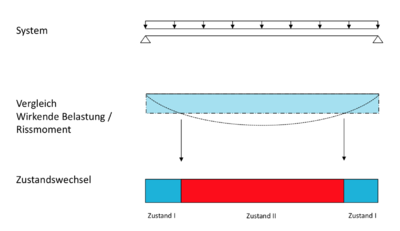
Die Differenzierung des Bauteiles zwischen den Zuständen I und II beschreibt maßgeblich das Verformungsverhalten des jeweiligen Bauteiles. Das Maß der Rissbildung beeinflusst die Steifigkeit der für die Durchbiegung betrachteten Querschnitte. Während im Zustand I der gesamte Querschnitt des bewehrten Betons in die Steifigkeitsberechnung beteiligt ist, wird die Steifigkeit im Zustand II vermindert. Die minimierte Steifigkeit führt folglich zu einer Vergrößerung der Durchbiegung.

Die Rissbildung des bewehrten Betonquerschnittes wird maßgebend charakterisiert durch das Verhalten des Betons unter Zug. Dargestellt wird dies mit Hilfe des Rissmomentes. Kommt es zur Überschreitung des Rissmomentes beginnen die Betonfasern in der Zugzone zu reißen. Die Spannungsnulllinie des Betons verschiebt sich, die Druckzone des Betons wird verkleinert.

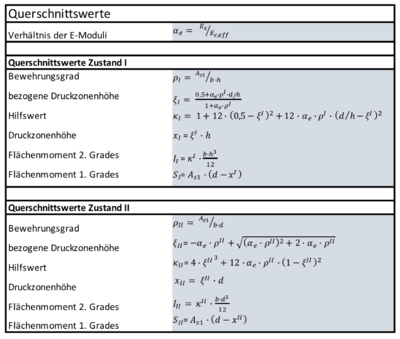
Vereinfacht wird in den Ansätzen zur Verformungsberechnung eine Differenzierung nach Zustand I, der Beton ist vollkommen ungerissen, und Zustand II, der Beton ist vollständig gerissen, vorgenommen. Folglich sind die Steifigkeiten für den reinen Zustand I und den reinen Zustand II in der Berechnung maßgebend. Eine Zusammenfassung der Querschnittswerte für den Zustand I und Zustand II lassen sich der Literatur entnehmen.

Statisch bestimmte Systeme

Die Schnittgrößenermittlung statisch bestimmter Systeme ist vereinfacht durch die Annahme, dass die Steifigkeit eines Bauteils konstant ist. Die Differenzierung nach Zustand I und Zustand II findet aufgrund dieses elastischen Verhaltens in der Schnittgrößenermittlung keine Relevanz. Für die Berechnung der Durchbiegung werden zwei Verfahren vorgeschlagen:

• Das Näherungsverfahren nach EC2
• Sowie die Durchbiegungsberechnung mit Hilfe einer numerischen Integration der Querschnittskrümmungen

Näherungsverfahren nach EC2

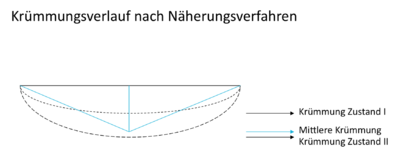
Das Ziel des Näherungsverfahrens nach EC2 ist im wesentlichen ein vereinfachter Vorschlag der Krümmung eines Stahlbetonbauteiles und liefert unter Beachtung des Rissverteilungsbeiwertes die mittlere zu erwartende Krümmung des betrachteten Bauteiles.

Die jeweils maximalen zu erwartenden Krümmungen des Zustand I und Zustand II werden berechnet. Dabei findet eine Differenzierung der Krümmung nach den Ursachen Last+Kriechen und Schwinden statt. Folglich ergeben sich vier unterschiedliche Krümmungen – jeweils zwei Größen für den Zustand I und Zustand II.

$\kappa =(1/r)={\frac {M}{EI}}$

$\kappa _{cs}=(1/r)_{cs}=\epsilon _{cs}\cdot \alpha _{e}\cdot S/I$

κ	Krümmung unter Last+Kriechen
κ cs	Krümmung unter Schwinden
E	Elastizitätsmodul
I	Flächenmoment 2. Grades
S	Flächenmoment 1. Grades
α e	Verhältnis der Elastizitätsmodule Stahl und Beton
ε cs	Endschwindmaß

Die Querschnittswerte zur Ermittlung der Steifigkeit können der [Tabelle] entnommen werden.

Das Kriechverhalten findet seine Beachtung durch den effektiven Elastizitätsmodul.

$E_{c,eff}={\frac {E_{cm}}{1+\phi (\infty ,t_{0})}}$

E cm	mittlerer Elastizitätsmodul Beton
φ(∞,t0)	Endkriechzahl

Zur Berechnung der mittleren Krümmung wird der Rissverteilungswert benötigt. Der Rissverteilungsbeiwert drückt dabei die Verteilung des Zustand I und Zustand II über die Bauteilachse aus und lässt sich nach folgendem Ansatz berechnen:

$\zeta =1-\beta \cdot ({\frac {\sigma _{sr}}{\sigma _{s}}})^{2}$

β	Beiwert zur Berücksichtigung der Belastungsdauer (=0,5 für Langzeitbelastungen; =1,0 für Kurzzeitbelastungen)
σsr	Stahlspannung unter Rissmoment
σs	Stahlspannung unter Belastung

Alternativ lässt sich der Quotient der Stahlspannungen durch den Quotient aus Rissmoment und Feldmoment ersetzen:

$\zeta =1-\beta \cdot ({\frac {M_{cr}}{M}})^{2}$

β	Beiwert zur Berücksichtigung der Belastungsdauer (=0,5 für Langzeitbelastungen; =1,0 für Kurzzeitbelastungen)
Mcr	Rissmoment
M	Moment aus Belastung

Rissmoment nach DafStb:

$M_{cr}=W_{el}\cdot f_{ctm}$

Wel	elastisches Widerstandsmoment
fctm	mittlere Betonzugfestigkeit

Man differenziert die Art der Belastung nach Kurzzeitbelastungen und Langzeitbelastungen. Langzeitbelastungen weisen dabei eine größere Krümmungsentwicklung auf als Kurzzeitbelastungen.

Prinzipdarstellung: Krümmungsverlauf nach Näherungsverfahren nach EC2

Die mittlere Krümmung des Bauteils lässt sich nachfolgend über Rissverteilungsbeiwert ermitteln. Folglich werden die Krümmungen unter Last+Kriechen und Schwinden addiert.

$(1/r)_{IIm}=\zeta \cdot (1/r)_{II}\cdot (1-\zeta )\cdot (1/r)_{I}$

ζ	Rissverteilungsbeiwert
(1/r)II	Krümmung im Zustand II
(1/r)I	Krümmung im Zustand I

Abschließend wird die Durchbiegung unter zu Hilfenahme der bereits erwähnten Krümmung unter Abhängigkeit der Systemlänge und dem Beiwert zur Berücksichtigung des Momentenverlaufs zu einer Durchbiegung überführt:

$w(l/2)=k\cdot \kappa \cdot l^{2}$

k	Beiwert zur Berücksichtigung des Momentenverlaufes
κ	Krümmung in Feldmitte
l	Systemlänge

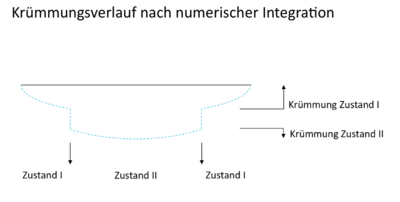
Numerische Integration

Die numerische Integration stellt ein Hilfsmittel zur Berechnung der Durchbiegungen eines Bauteils dar. Der größere Rechenaufwand ermöglicht eine genauere Differenzierung zwischen den Zuständen I und II des Stahlbetonbauteils. Das Bauteil wird in eine beliebige Anzahl an Intervallen unterteilt, je höher die Anzahl der betrachteten Querschnitte gewählt wird, desto genauer lässt sich die Durchbiegung ermitteln. Für eine genaue Näherung an die Durchbiegung reicht bereits eine Unterteilung in 9 Stützstellen – also 8 Intervallen –, eine Vergrößerung der Einteilung auf bis zu 21 Stützstellen liefert letztlich keine weitere Verbesserung mehr und der erheblich größere Rechenaufwand steht mit dem Ergebnis nicht mehr in einem vertretbaren Rahmen.

Die grundlegende Annahme ist auch hier der Zusammenhang aus Krümmung, Belastung und Steifigkeit des Querschnittes:

$\kappa =(1/r)={\frac {M}{EI}}$

Durch doppelte Integration lässt sich die Durchbiegung ermitteln:

$w(x)=\int _{}^{}\int _{}^{}{\frac {M(x)}{EI(x)}}dx$

Unter Ansatz des Prinzips der virtuellen Kräfte lässt sich das Doppelintegral vereinfachen:

$w(x)=\int _{}^{}{\frac {{\overline {M}}(x)\cdot M(x)}{EI(x)}}dx=\int _{}^{}({\overline {M}}(x)\cdot \kappa )dx$

Mit Hilfe der Simpson-Gleichung und unter Annahme von einer Unterteilung auf Basis von 9 Stützstellen lässt sich Integral in Form eines Summenansatzes lösen:

$w(x)={\frac {\Delta x}{3}}\cdot (2y_{0}+8y_{1}+4y_{2}8+y_{3}+2y_{4})$

Mit:

$y_{n}=\kappa _{n}\cdot {\overline {M}}_{n}$

Für jeden betrachteten Querschnitt n werden die virtuellen Momentenschnittgrößen ermittelt. Er ergeben sich folgende Momente unter einer virtuellen Last der Größe 1 in Feldmitte:

${\overline {M}}_{1}={\frac {1}{16}}l$

${\overline {M}}_{2}={\frac {1}{8}}l$

${\overline {M}}_{3}={\frac {3}{16}}l$

${\overline {M}}_{4}={\frac {1}{4}}l$

Prinzipdarstellung: Krümmungsverlauf nach numerischer Integration

Durch die Symmetrie des Momentenverlaufes und Krümmungsverlaufes genügt die Betrachtung einer Hälfte des Trägers.

Nach Einsetzen in den Ansatz nach der Simpson-Gleichung ergibt sich die Durchbiegung zu:

$w(l/2)={\frac {l^{2}}{96}}\cdot (2\kappa _{1}+2\kappa _{2}+6\kappa _{3}+2\kappa _{4})$

Anhand dieser Gleichung lassen sich die Durchbiegungen beliebiger Einfeldsysteme berechnen. Unbekannte Größen sind dabei nur noch die n Querschnittskrümmungen.

Prinzipdarstellung: Beurteilung des Zustandwechsels anhand der Ordinaten x_cr,1;2

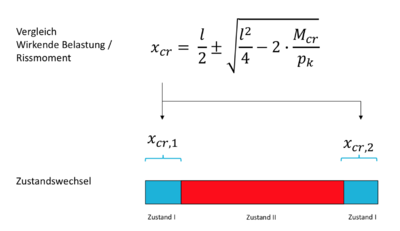
Eine Differenzierung zwischen den Zuständen I und II lässt sich über folgenden Ausdruck ermitteln:

$x_{cr}={\frac {l}{2}}\pm {\sqrt {{\frac {l^{2}}{4}}-2\cdot {\frac {M_{cr}}{p_{k}}}}}$

Mcr	Rissmoment
pk	Belastung

Der Ansatz liefert zwei Ordinaten: erstere gibt Aufschluss über den Wechsel von Zustand I in den Zustand II; zweitere gibt Aufschluss über den Wechsel von Zustand II in den Zustand I.

Die für die Querschnittskrümmungen relevanten Querschnittswerte lassen sich mit den Formeln nach [Stahlbetonbau-Praxis S. 270,271] ermitteln. Für die Differenzierung der Zustände I und II werden die Lagen der n Krümmungen auf der Bauteilachse betrachtet und errechnet.

Unter Annahme einer konstanten Gleichstreckenlast und Steifigkeit – also unter Vernachlässigung der Zustände I und II – lässt sich die numerische Integration vereinfachen zu:

$w(l/2)={\frac {5}{384}}\cdot {\frac {p_{k}l^{4}}{EI}}$

Mit dieser Vereinfachung lässt sich die Durchbiegung getrennt für die Zustände I und II berechnen und abschließend analog zum Näherungsverfahren unter Annahme des Rissverteilungsbeiwertes zu einer erwarteten mittleren Krümmung errechnen.

Die Abweichungen zwischen dem Näherungsverfahren nach EC2 und der numerischen Integration belaufen sich ungefähr im Rahmen von 4%; für die Baupraxis ist die Berechnung nach dem Näherungsverfahren genau genug.

Statisch unbestimmte Systeme

Prinzipdarstellung: Abhängigkeiten der Krümmungsberechnung statisch unbestimmter Systeme

Die Schnittgrößenermittlung statisch unbestimmter Systeme steht in direktem Zusammenhang zu der Steifigkeitsentwicklung des Bauteiles. Die Differenzierung nach Zustand I und Zustand II hat somit maßgeblich einen Einfluss auf die Schnittgrößenermittlung und folglich gestaltet sich die Ermittlung der Durchbiegung als ein iterativer Prozess. Die Einschätzung nach Zustand I und Zustand II ist direkt gekoppelt an die Schnittgrößen, diese wiederum im Falle statisch unbestimmter Systeme an die Steifigkeiten des Bauteiles, die unter Beachtung der Rissbildung abgeschätzt wird. Folglich muss die Durchbiegung eines statisch unbestimmten Systems in mehreren – iterativen – Rechnungen durchgeführt werden, solange bis die Durchbiegung als abgeschlossen angenommen werden kann.

Quellen

Seiteninfo Status: Seite in Bearbeitung