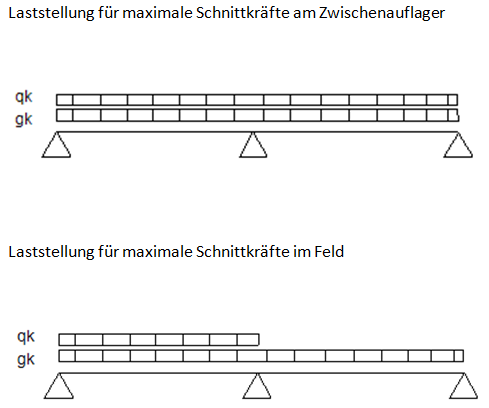
Nachweisführung und Bewehrungsermittlung vergleichend zur MB-Baustatik (Effektive Plattenbreite und Schnittkraftermittlung)

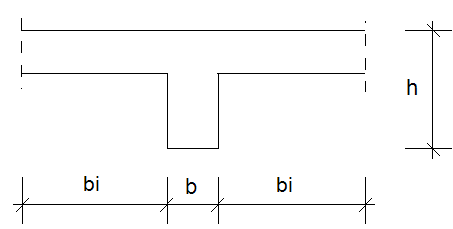
Effektive Plattenbreite

• Effektive Plattenbreite im Feld:

$b_{eff}=\sum b_{eff,i}+b$

$b_{eff,i}=0,2\cdot b_{i}+0,1\cdot l_{0}{\begin{cases}\leq 0,2\cdot l_{0}\\\leq b_{i}\end{cases}}$

$=0,2\cdot 1,20+0,1\cdot (0,85\cdot 6,50)={\underline {\underline {0,7925}}}{\begin{cases}\leq 0,2\cdot (0,85\cdot 6,50)=1,105\\\leq 1,20\end{cases}}$

$b_{eff,1}=2\cdot 0,7925+0,30={\underline {\underline {1,885m}}}$

• Effektive Plattenbreite am Zwischenauflager:

$b_{eff,i}=0,2\cdot 1,20+0,1\cdot (0,15\cdot 13)=0,435{\begin{cases}\leq 0,2\cdot (0,15\cdot 13)={\underline {\underline {0,39}}}\\\leq 1,20\end{cases}}$

$b_{eff,1}=2\cdot 0,39+0,30={\underline {\underline {1,08m}}}$

MB-Ausdruck:

Schnittgrößenermittlung