Ziel der Bemessung bzw. des Nachweises eines überwiegend beanspruchten Bauteils ist nachzuweisen, dass der Querschnitt die äußeren Schnittgrößen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Ed}} ) im Grenzzustand der Tragfähigkeit aufnehmen kann. Bei der Bemessung wird das aufnehmbare Moment durch die Veränderung der Bewehrungsquerschnittsfläche an die vorhandenen äußeren Schnittgrößen angepasst. Beim Nachweis eines biegebeanspruchten Bauteils wird für eine gegebene Bewehrung überprüft, ob die aufnehmbaren Schnittgrößen die einwirkenden Schnittgrößen übersteigt.

$M_{Ed}\leq M_{Rd}\qquad \qquad N_{Ed}\leq N_{Rd}$

Tragverhalten

Dehnungsbereiche

Beeinflusst wird die Tragfähigkeit von Biegebauteilen durch die Festigkeiten von Stahl und Beton sowie durch die Querschnittswerte (Breite, Höhe und Form der Druckzone, statische Nutzhöhe, Bewehrungsquerschnittsfläche).

Die Bemessung im Grenzzustand setzt voraus, dass die Bruchdehnung der Bewehrung oder des Betons überschritten wird und dementsprechend ein Stahl- oder Betonversagen eintritt (vgl. Bild… und Bild …). Abhängig von der Beton- und Stahldehnung können dabei fünf Dehnungsbereiche unterschieden werden:

Dehnungsbereiche 1: Im gesamten treten ausschließlich Zugdehnungen auf. Die Bewehrung erreicht ihre Bruchdehnung von 25\textperthousand, das Versagen findet durch das Versagen der Bewehrung statt. Da vor dem Versagen die Fließgrenze überschritten wird, findet eine Ankündigung des Versagens durch breite Risse statt.

Dehnungsbereiche 2: Die Grenzdehnung der Zugbewehrung wird erreicht, in der Druckzone sind noch Tragreserven vorhanden. Das Versagen findet durch Versagen der Zugbewehrung mit Vorankündigung statt.

Dehnungsbereiche 3: Die Fließgrenze des Stahls wird überschritten, die Bruchdehnung der Bewehrung wird aber nicht erreicht. Die Bruchdehnung der Betondruckzone wird erreicht. Das Versagen findet durch das Versagen der Betondruckzone statt. Trotz des Betonversagens findet eine Versagensankündigung statt, da der Stahl vor dem Bruch plastizieren kann.

Dehnungsbereiche 4: Der Stahl erreicht die Fließgrenze nicht, die Bruchdehnung des Betons wir überschritten. Die maßgebende Versagensart ist das Betonversagen, da die Stahldehnung unter der Fließgrenze bleibt, findet keine Vorankündigung des Versagens statt. Da wegen der geringen Stahldehnung nicht die volle Zugfestigkeit des Stahls aktiviert wird, ergibt die Bemessung in diesem Bereich große, unwirtschaftliche Bewehrungsquerschnittsflächen.

Dehnungsbereiche 5: Im gesamten Querschnitt treten nur Druckbeanspruchungen auf. Das Versagen findet durch Versagen des Betons ohne Vorankündigung statt.

Für überwiegend biegebeanspruchte Bauteile sind die Dehnungsbereiche 2 bis 4 relevant. Querschnitt im Dehnungsbereich 1 und 5 sind überwiegend längskraftbeansprucht. Bei der Bemessung ist stets ein Versagen mit Vorankündigung anzustreben, die Querschnitte sollten sich dementsprechend in den Dehnungsbereichen 2 oder 3 befinden.

Die Biegebemessung im Grenzzustand der Tragfähigkeit hat die Aufgaben,

nachzuweisen, dass der vorab gewählte Betonquerschnitt in der Lage ist die vorhandenen Druckspannungen aufzunehmen und

die erforderliche Stahlquerschnittsfläche der Biegezugbewehrung an den Stellen der maximalen Biegebeanspruchung zu bestimmen.

Um eine Bemessung des Querschnitts im Grenzzustand der Tragfähigkeit zu ermöglichen, werden im Voraus folgende grundlegende Annahmen getroffen:^[1]

Querschnitte, die vor der Verformung eben waren, bleiben eben (Bernoulli Hypothese)

Es liegt vollkommener Verbund vor, das heißt die Dehnungen des Betons entsprechen den Dehnungen des Betonstahls

Die Zugfestigkeit des Betons darf im Grenzzustand der Tragfähigkeit nicht berücksichtigt werden, das heißt sämtliche Zugkräfte müssen durch den Betonstahl aufgenommen werden

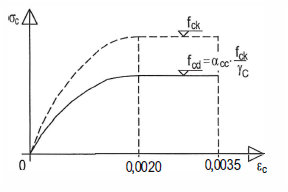
Für die Spannungs-Stauchungs- Verknüpfung im Beton gilt im Regelfall folgendes vereinfachtes Diagramm:

Gilt für Betone der Festigkeitsklasse bis C50/60 bzw. Leichtbetone bis C50/55

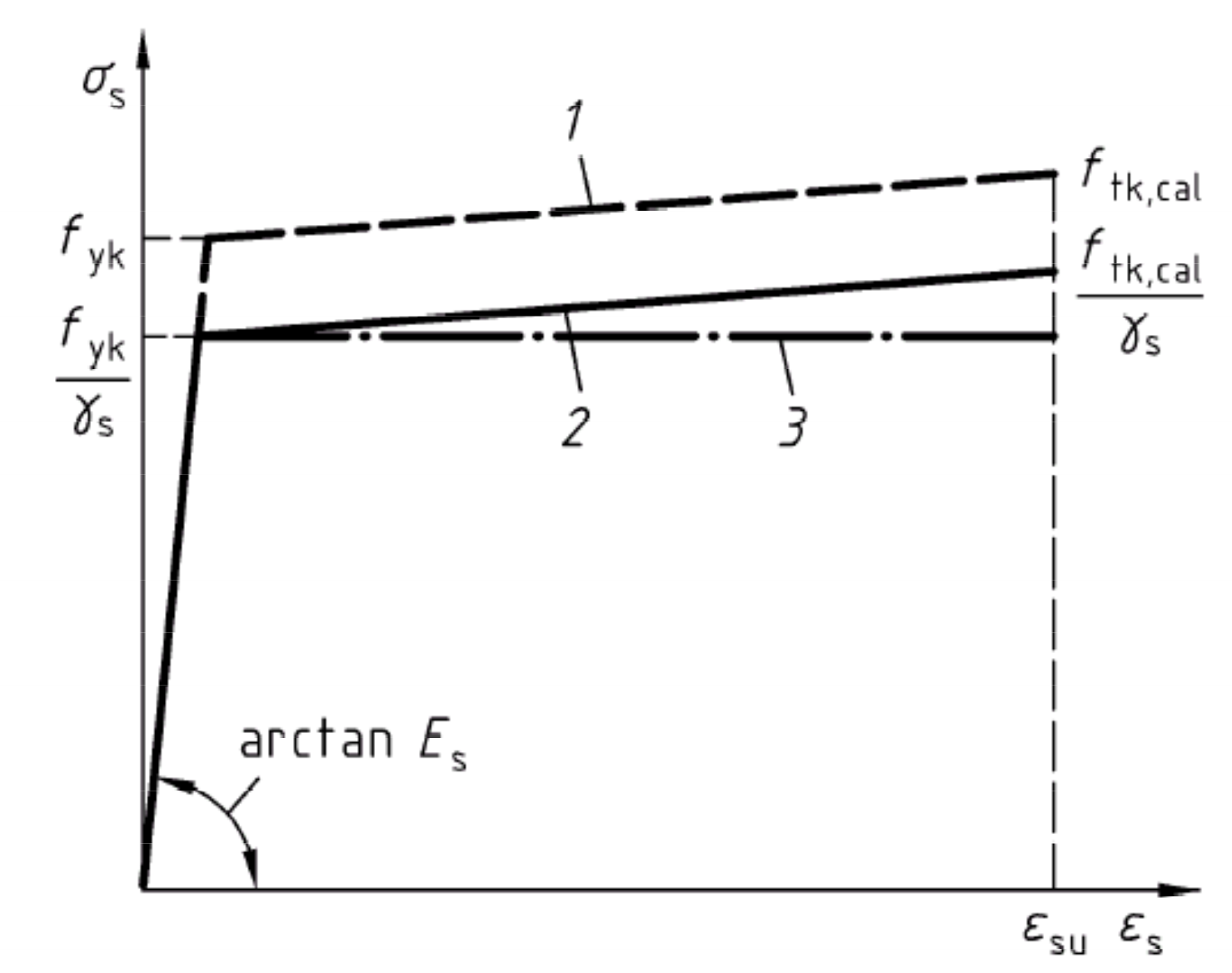
Die Spannungs-Dehnungs/Stauchungs-Verhältnisse im Stahlbeton werden für die Bemessung wie folgt beschrieben:

Linie I: Zur Vereinfachung wird ein horizontal weiterlaufender Ast angenommen f_yk=500N/mm²

Linie II: Ansteigender Ast zugelassen zur Querschnittsbemessung, wenn die Dehnung maximal ε_ud=25 ‰ beträgt

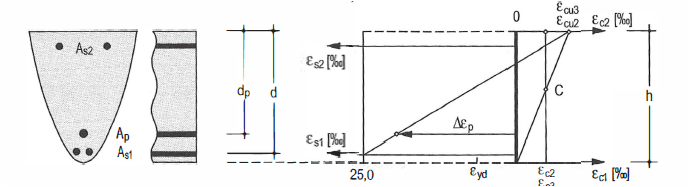
Es gelten folgende möglichen Dehnungsverteilungen im Stahlbetonquerschnitt:^[2]

Für Betone bis zur Festigkeitsklasse C50/60 gelten die Grenzstauchungen:

ε_c2=-3,5‰ bei Biegebeanspruchung und

ε_c2=ε_c1=-2,2‰ bei zentrischem Druck

Der Betonstahl versagt bei einer Grenzdehnung von ε_s1=ε_s2=25‰

Nachweisführung und Bewehrungsermittlung mit Bemessungshilfen

Eine iterative Handrechnung ist in der Praxis sehr umständlich und daher nicht üblich.

Der Nachweis der Grenztragfähigkeit und die Ermittlung der Längsbewehrung erfolgen im Allgemeinen mit Bemessungstafeln, wie sie beispielsweise in [Schneider Bautabellen für Ingenieure 20.Auflage Abs.5.6 Tafeln 1-9] zu finden sind.^[3]

Um mit den Bemessungshilfen arbeiten zu können, müssen die Bauteilabmessungen und Materialparameter bekannt sein.

Die statische Nutzhöhe d kann für den Fall, dass sie vor der Bewehrungsermittlung noch unbekannt ist über eine Vorbemessung

abgeschätzt werden und gegebenenfalls nach der Bewehrungswahl noch einmal korrigiert werden und für eine erneute Bemessung verwendet werden.

Mit Hilfe der Bemessungstafeln bzw. Diagrammen kann nun bei bekanntem maximalen einwirkenden Moment die erforderliche Bewehrung,

oder bei bekanntem Bewehrungsquerschnitt das maximal aufnehmbare Moment ermittelt werden.

Um die Verwendung der Hilfsmittel Querschnittsunabhängig und damit allgemein anwendbar zu machen, werden verschiedene dimensionslose bezogene Parameter entwickelt:^[2]^[4]

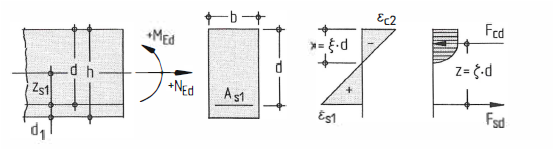
Einwirkende Schnittgrößen müssen auf die mit Hilfe von zs1 auf den Schwerpunkt der Bewehrung übertragen werden:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Eds}=M_\mathrm{Ed}-N_\mathrm{Ed}\cdot z\mathrm{s1}~} (entfällt im Modul S340.de, da keine Normalkraft definierbar)

Das bezogene Moment in der Höhe der gesuchten Bewehrung ergibt sich zu:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_\mathrm{Eds}=\cfrac{M_\mathrm{Eds}}{b\cdot d^2 \cdot f_\mathrm{cd}}~}

Die Betondruckkraft Fcd ergibt sich, indem die Fläche der Druckspannungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_\mathrm{cd}~} über die Druckzonenhöhe $x~$ integriert wird:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{cd}=\int_0^x \sigma_\mathrm{cd}\cdot b \cdot dz~}

Mit dem Völligkeitsbeiwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_{R}~} , der das Verhältnis der integrierten Fläche zur einhüllenden Rechteckfläche beschreibt, ergbibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{cd}=\alpha_{R}\cdot b\cdot x\cdot f_{cd}~}

Es wird eine bezogene Druckzonenhöhe eingeführt: $\xi ={\cfrac {x}{d}}~$ bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=\xi\cdot d~}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{cd}=\alpha_{R}\cdot b\cdot \xi\cdot d\cdot f_{cd}~} oder auch: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cfrac{F_{cd}}{b\cdot d\cdot f_{cd}}= \alpha_{R}\cdot \xi ~}

Mit dem Bauteilwiderstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Rds}=F{cd}\cdot z~} und der Aussage: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Eds}=M_{Rds}~} und dem bezogenen Moment:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}=\cfrac{M_{Eds}}{b\cdot d^2\cdot f_{cd}}=\cfrac{F_{cd}}{b\cdot d\cdot f_{cd}}\cdot \cfrac{z}{d}~}

Es wird ein bezogener innerer Hebelarm Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta~} eingeführt aus:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=k\cdot x=k_{a}\cdot \xi \cdot d~} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z= d- a= (1- k_{a}\cdot \xi)\cdot d= \zeta\cdot d~}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=~} Abstand von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{cd}~} zur oberen Bauteilkante

Aus allen jetzt bekannten Beziehungen ergibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}= \cfrac{\alpha_{R}\cdot b\cdot \xi\cdot d\cdot f_{cd}}{b\cdot d\cdot f_{cd}}\cdot \cfrac{(1-k_{a}\cdot \xi)\cdot d}{d}~}

⇒ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\mu_{Eds}= \alpha_{R}\cdot \xi\cdot \zeta}~}

Die erforderliche Bewehrung lässt sich wie folgt ermitteln:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Rd}= F_{sd}- F_{cd}~} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Ed}= N_{Rd}~}

⇒Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd}= F_{cd}+ N_{Ed}~}

Mit bekanntem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Eds}= F_{cd}\cdot z~} ergibt sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd}=\cfrac{M_{Eds}}{z}+N_{Ed}~}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd}= \sigma_{sd}\cdot A_{s}~} unter der Annahme Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{sd}=f_{yd}~}

⇒Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{A_{s}=\cfrac{1}{f_{yd}}\cdot (\cfrac{M_{Eds}}{z}+N_{Ed})}~}

Die hergeleiteten dimensionslosen Parameter hängen nur von dem vorgegebenen Dehnungsverhältnis ab, nicht aber von den Abmessungen des Bauteils.

Werden die Beziehungen für alle zulässigen Dehnungsverhältnisse ausgewertet, können Bemessungshilfen erstellt werden,

mit denen bei bekanntem Dehnungsverhältnis, das aufnehmbare Moment und die erforderliche Bewehrung, ermittelt werden können.

Allgemeines Bemessungsdiagramm

Allgemeines Bemessungsdiagramm^[1]

Das allgemeine Bemessungsdiagramm ist für alle Normalbetone bis zur Festigkeitsklasse C50/60 anwendbar.

Als Eingangswert dient entweder das bezogene Moment

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}= \cfrac{M_{Eds}}{b\cdot d^2\cdot f_{cd}}~}

Es können alle dazugehörigen Parameter und die Dehnungsverteilung abgelesen werden und die erforderliche Bewehrung mit:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}=\cfrac{1}{f_{yd}}\cdot (\cfrac{M_{Eds}}{z}+ N_{Ed})~} ermittelt werden.

Oder, bei bekannter Bewehrungsquerschnittsfläche, der Druckzonenparameter:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{cd}=\cfrac{f_{yd}\cdot A_{s}}{f_{cd}\cdot b\cdot d}~}

Damit kann das bezogene Moment abgelesen und die Tragfähigkeit durch umstellen der Formel zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Eds}=\mu_{Eds}\cdot f_{cd}\cdot b\cdot d~} ermittelt werden.

Hinweis: Bei Verwendung des Diagramms sind immer geringe Ableseungenauigkeiten zu erwarten

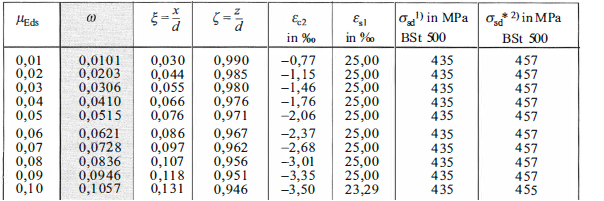
Bemessungstafeln mit dimensionslosen Beiwerten (Omega-Verfahren)

Die Bemessungstafeln zeigen das allgemeine Bemessungsdiagramm in tabellierter Form, erweitert um den mechanischen Bewehrungsgrad Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega~} ^[2]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega=\cfrac{A_{s}\cdot \sigma_{sd} - N_{Ed}}{b\cdot d\cdot f_{cd}}~}

Mit bekanntem Moment dient wieder das bezogene Moment Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}~} als Einganswert und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega~} kann abgelesen werden (Entweder ungünstigerer Wert oder interpolieren)

und über die Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}=\cfrac{1}{\sigma_{sd}}\cdot (\omega\cdot b\cdot d\cdot f_{cd} + N_{Ed})~} der erforderliche Bewehrungsquerschnitt ermittelt werden.

Bei bekanntem Querschnitt kann durch umstellen der Formel zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega= \cfrac{A_{s}\cdot f_{yd}}{f_{cd}\cdot b\cdot d}~} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega~} als Eingangswert verwendet werden.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}} kann abgelesen werden und das aufnehmbare Moment ermittelt werden.

Auszug aus dimensionsloser Tabelle:^[1]

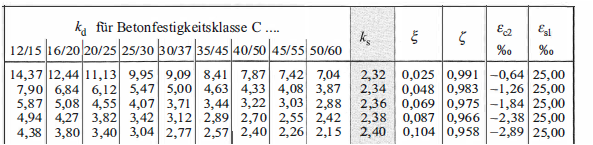
Bemessungstafeln mit dimensionsgebundenen Beiwerten (kd–Verfahren)

Für das kd-Verfahren werden dimensionsgebundene, von der Festigkeitsklasse abhängige Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{d}~} -Beiwerte ermittelt. ^[2]

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle k_{d}={\cfrac {d[cm]}{\sqrt {M_{Eds}[kNm]/b[m]}}}~}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{s}~} - Wert wird abgelesen und der Stahlquerschnitt ermittelt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}[cm^2]=k_{s}\cdot \cfrac{M_{Eds}[KnM]}{d[cm]}+ \cfrac{N_{Ed}[kN]}{43,5}~}

Bei bekanntem Querschnitt wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{s}~} durch entsprechendes umstellen der Formel ermittelt,

-> Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{d}~} abgelesen und das aufnehmbare Moment ermittelt.

Auszug aus dimensionsgebundener Tabelle:^[1]

Mit steigender Belastung, steigt auch das bezogene Moment und die Höhe der Druckzone, so kann es bei zu hohen

Beanspruchungen der Druckzone zu einem unangekündigtem Versagen kommen.

Aus diesem Grunde wird die bezogene Höhe der Druckzone auf den Wert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi_{lim}~} begrenzt.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi_{lim}~} lässt sich folgendermaßen ermitteln: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi_{lim}=\cfrac{\epsilon_{cu2}}{\epsilon_{cu2}-\epsilon_{sy}}~}

Für Normalbetone <C50/60 ergibt sich aufgrund der selben Randstauchung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon_{cu2}~} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi_{lim}=0,617~}

Sollte dieser Grenzwert überschritten werden, muss die Druckzone durch zusätzliche "Druckbewehrung" verstärkt werden.

Hierzu gibt es ebenfalls Bemessungshilfen.

Bei Plattenbalken, die mit der Platte in der Druckzone liegen, muss keine Druckbewehrung angeordnet werden.

Vorgehensweise Plattenbalken

Bei der Biegebemessung von Plattenbalken ist zunächst die Mitwirkende Plattenbreite zu ermitteln.

Befindet sich die Platte in der Druckzone, ist das bezogene Moment Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Eds}~} mit der effektiven Plattenbreite zu ermitteln^[4]

Mit dem bezogenen Moment als Eingangswert wird aus der Tafel für Rechteckquerschnitte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi~} abgelesen.

Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi < \cfrac{h_{f}}{d}~} liegt die Dehnungsnulllinie in der Platte und die Bemessung kann wie bei einem Rechteckquerschnitt erfolgen.

Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi > \cfrac{h_{f}}{d}~} liegt die Dehnungsnulllinie im Steg und es muss mit gesonderten Tafeln für Plattenbalken gearbeitet werden.

Im Bereich negativer Momente muss ebenfalls die Lage der Dehnungsnulllinie geprüft werden,

sollte sie im Steg liegen ist ebenso wie bei einem Rechteckquerschnitt vorzugehen mit der Breite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b=~} Stegbreite.

Um die richtige Tafel für Plattenbalkenquerschnitte zu wählen müssen die Verhältnisse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cfrac{h_{f}}{d}~} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cfrac{b_{f}}{b_{w}}~} ermittelt werden.

Anschließend kann aus der passenden Tafel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega~} abgelesen werden und die Querschnittsfläche der Bewehrung über

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}=\cfrac{1}{f_{yd}}\cdot (\omega\cdot b_{f}\cdot f_{cd}+ N_{Ed})~}

errechnet werden.

Quellen

↑ ^1,0 ^1,1 ^1,2 ^1,3 Schneider Bautabellen für Ingenieure, 20. Auflage, Köln: Werner Verlag, 2012
↑ ^2,0 ^2,1 ^2,2 ^2,3 Avak,R., Conchon,R., Aldejohann,M., Stahlbetonbau in Beispielen Teil 1, 7. Auflage, Nürnberg/Düsseldorf: Bundesanzeiger Verlag, 2016
↑ Goris,A., Stahlbetonbau-Praxis nach Eurocode 2, Band 1, 5. Auflage, Siegen: Beuth, 2014
↑ ^4,0 ^4,1 Bolle,G., Skript Stahlbetonbau 1, Themenkomplex 5- Bemessung bei überwiegender Biegung im Grenzzustand der Tragfähigkeit (Rechteckquerschnitt), Wismar, 2014

Seiteninfo

Status: in Bearbeitung

Modul-Version: 2016.0500

[Name_der_Quelle-1] 1,0 ^1,1 ^1,2 ^1,3 Schneider Bautabellen für Ingenieure, 20. Auflage, Köln: Werner Verlag, 2012

[Name_der_Quelle1-2] 2,0 ^2,1 ^2,2 ^2,3 Avak,R., Conchon,R., Aldejohann,M., Stahlbetonbau in Beispielen Teil 1, 7. Auflage, Nürnberg/Düsseldorf: Bundesanzeiger Verlag, 2016

[3] Goris,A., Stahlbetonbau-Praxis nach Eurocode 2, Band 1, 5. Auflage, Siegen: Beuth, 2014

[Name_der_Quelle2-4] 4,0 ^4,1 Bolle,G., Skript Stahlbetonbau 1, Themenkomplex 5- Bemessung bei überwiegender Biegung im Grenzzustand der Tragfähigkeit (Rechteckquerschnitt), Wismar, 2014

[1]

[2]

[3]

[4]

Biegebemessung (einachsige Biegung)

Inhaltsverzeichnis