Auf dieser Seite wird die Anwendung des Näherungsverfahren zur direkten Verformungsberechnung nach EC2 an einem ausgewählten Beispiel dargestellt. Die theoretischen Grundlagen der direkten Verformungsberechnung werden auf einer gesonderten Seite dargestellt.

Aufgabenstellung

Ein Balken mit Rechteckquerschnitt wird im Grenzzustand der Gebrauchstauglichkeit durch eine Gleichlast in Höhe von 40 kN/m belastet. Der Beton hat eine Festigkeitsklasse C20/25. Für das gegebene Bauteil ist unter gegebener Belastung die Verformung in Balkenmitte zu ermitteln.

l_eff=6m
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_{Ed,perm}=66,5\frac{kN}{m}} (Kurzzeitbelastung)
b/h=35cm/75cm
d=70cm
B500A
Längsbewehrung: 4⌀25 (A_s,vorh=19,64cm²)
C 20/25
ε_cs=0,4‰
φ (∞,t₀)=2

Festigkeiten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ctm}=2,2 \frac{N}{mm^2}=0,22\frac{kN}{cm^2}}

Vorbereitende Berechnung

Ermittlung des quasi-ständigen Moments

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed,perm}=\frac{p_{Ed,perm}\cdot l^2}{8}=\frac{66,5\cdot6^2}{8}=299,25kNm}

Ermittlung des Rissbildungsmoments

$z_{I}={\frac {75}{2}}=37,5cm$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_{I}=\frac{b\cdot h^3}{12}=\frac{35\cdot75^3}{12}=1230468cm^4}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{cr}=f_{ctm}\cdot\frac{I_I}{z_I}=0,22\cdot\frac{1230468}{37,5}=7219kNcm}

Ermittlung des effektives Elastizitätsmodul

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_{cm}=30000\frac{N}{mm^2}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_{c,eff}=\frac{E_{cm}}{1+\phi_{\infty,t_0}}=\frac{30000}{1+2}=10000\frac{N}{mm^2}=1000\frac{kN}{cm^2}}

Ermittlung der Druckzonenhöhe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_e=\frac{E_s}{E_{c,eff}}=\frac{200000}{10000}=20 }

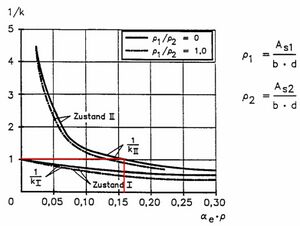
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_l=\frac{A_s}{b\cdot d}=\frac{19,64}{35\cdot 70}=0,008 }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_l\cdot \alpha_e=20\cdot0,008=0,16 }

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle x=\xi \cdot d=d\cdot \left(-\alpha _{e}\cdot \rho _{l}+{\sqrt {(\alpha _{e}\cdot \rho _{l})^{2}+2\cdot \alpha _{e}\cdot \rho _{l}}}\right)}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=70\cdot\left(-0,16+\sqrt{0,16^2+2\cdot0,16}\right)}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=29,95cm}

Ermittlung der Krümmung

Krümmung im Zustand I

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_I = \left(\frac{1}{r}\right)_{I} = \frac{M_{Ed}}{E_{c,eff}\cdot I_I}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_I = \frac{29925}{1000\cdot1230468 }=2,43\cdot 10^{-5}\frac{1}{cm}=2,43\cdot 10^{-3}\frac{1}{m}}

Krümmung im Zustand II

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_s=\frac{M_{Ed}}{A_s\cdot\left(d-\frac{x}{3}\right)}=\frac{29925}{19,64\cdot\left(70-\frac{29,95}{3}\right)}=25,39\frac{kN}{cm^2}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_s=\frac{\sigma_s}{E_s}=\frac{25,39}{20000}=1,27\cdot 10^{-3}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{II} = \left(\frac{1}{r}\right)_{II} = \frac{\varepsilon_s}{d-x}}

$\kappa _{II}={\frac {1,27\cdot 10^{-3}}{70-29,95}}=3,17\cdot 10^{-5}{\frac {1}{cm}}=3,17\cdot 10^{-3}{\frac {1}{m}}$

Krümmung - wahrscheinlicher Wert

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta=1,0}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \zeta=1-\beta\cdot\left(\frac{M_{cr}}{M_{Ed}}\right)^2=1-1\cdot\left(\frac{7219}{29925}\right)^2=0,942}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_m=\left(\frac{1}{r}\right)_m=\zeta\cdot\left(\frac{1}{r}\right)_{II}+\left(1-\zeta\right)\cdot\left(\frac{1}{r}\right)_{I}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_m=\left(\frac{1}{r}\right)_m=0,942\cdot3,17\cdot 10^{-3}+\left(1-0,942\right)\cdot2,43\cdot 10^{-3}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\kappa_m=3,13\cdot 10^{-3}}}

Ermittlung der Krümmung infolge Schwinden

Krümmung im Zustand I

Steifigkeitsbeiwert für den Zustand II^[1]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{cs,I}=\left(\frac{1}{r}\right)_{cs}=\varepsilon_{cs}\cdot\alpha_e\cdot\frac{S_I}{I_I} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_{I}=1230468cm^4}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_{s1}=\frac{h}{2}-(h-d)=\frac{75}{2}-(75-70)=32,5cm }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S_I=A_s\cdot z_{s1}=19,64\cdot 32,5=638,3cm^3 }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{cs,I}=\frac{0,4}{1000}\cdot20\cdot\frac{638,3}{1230468}=4,15\cdot 10^{-6}\frac{1}{cm}=4,15\cdot 10^{-4}\frac{1}{m} }

Krümmung im Zustand II

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{cs,II}=\left(\frac{1}{r}\right)_{cs}=\varepsilon_{cs}\cdot\alpha_e\cdot\frac{S_{II}}{I_{II}} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{II}=1}

$I_{II}=k_{II}\cdot I_{I}=1\cdot 1230468=1230468$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S_{II}=A_s\cdot \left(d-x\right)=19,64\cdot\left(70-29,95\right)=786,58cm^3 }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{cs,II}=\frac{0,4}{1000}\cdot20\cdot\frac{786,58}{1230468}=5,11\cdot 10^{-6}\frac{1}{cm}=5,11\cdot 10^{-4}\frac{1}{m} }

Krümmung - wahrscheinlicher Wert

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{cs,m}=\left(\frac{1}{r}\right)_{cs,m}=\zeta\cdot\left(\frac{1}{r}\right)_{cs,II}+\left(1-\zeta\right)\cdot\left(\frac{1}{r}\right)_{cs,I}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{cs,m}=0,942\cdot5,11\cdot 10^{-4}+\left(1-0,942\right)\cdot4,15\cdot 10^{-4}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\kappa_{cs,m}=5,05\cdot 10^{-4}\frac{1}{m}}}

Ermittlung der Gesamtkrümmung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{m,tot}=\left(\frac{1}{r}\right)_{m,tot}=\left(\frac{1}{r}\right)_{m}+\left(\frac{1}{r}\right)_{cs,m}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_{m,tot}=3,13\cdot 10^{-3}+5,05\cdot 10^{-4}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\underline {\kappa _{m,tot}=3,64\cdot 10^{-3}}}}

Ermittlung der Durchbiegung

=>Einfeldträger, Gleichlast (Beiwert nach LITZNER ^[2] vgl. Direkte Verformungsberechnung - biegebeanspruchte Bauteile)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\frac{5}{48}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=k\cdot l^2\cdot\left(\frac{1}{r}\right)_{m,tot}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=\frac{5}{48}\cdot 6^2\cdot3,64\cdot 10^{-3}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\underline {\underline {w=0,014m=1,4cm}}}}

Vergleich mit der direkten Verformungsberechnung mittels numerischer Integration

Auf der Seite zur direkten Verformungsberechung mittels numerischer Integration wird das hier vorgestellte Beispiel mit der numerischen Integration wiederholt.

Quellen

↑ Deutscher Aussschuss für Stahlbeton: Bemessungshilfen zu Eurocode 2, Teil 1, Planung von Stahlbeton und Spannbetonwerken; DAfStb Heft 425
↑ Litzner, H.-U.: Grundlagen der Bemessung nach Eurocode 2, BK 1995

Seiteninfo

Status: in Bearbeitung

[1] Deutscher Aussschuss für Stahlbeton: Bemessungshilfen zu Eurocode 2, Teil 1, Planung von Stahlbeton und Spannbetonwerken; DAfStb Heft 425

[2] Litzner, H.-U.: Grundlagen der Bemessung nach Eurocode 2, BK 1995

[1]

[2]

Verformungsnachweis - direkte Berechnung - Näherungsverfahren (Bsp.)

Inhaltsverzeichnis