Riss-vor-Bruch-Kriterium (Bsp.)

Auf dieser Seite wird der Nachweis Riss-vor-Bruch an einem ausgewählten Beispiel dargestellt. Die theoretischen Grundlagen des Nachweises werden auf einer gesonderten Seite dargestellt.

Aufgabenstellung

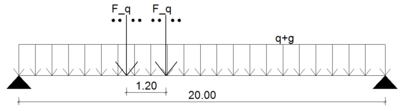
Der Nachweis Riss-vor-Bruch soll für den Haupträger mit Rechteckquerschnitt (b=100cm; h=100cm) einer 20m langen Straßenbrücke durchgeführt werden. Bei dem statischen System handelt es sich um einen Einfeldträger. Die verwendeten Materialien sind der nachfolgenden Auflistung zu entnehmen. Die Vorspannung erfolgte mit sofortigem Verbund

Lastanordnung und statisches System

• l_eff=20m (Einfeldträger)
• b=100cm
• h=100cm
• d_s=93cm
• d_p=85cm
• A_s1=31,42cm^2 (BSt IV; f_yk=550 N/mm²)
• A_p=65cm^2 (Hennigsdorfer Spannstahl St 140/160; f_pk=1370 N/mm²)
• E_p=205000
• σ_pp=800 N/mm²
• B 600 (f_ck=33 N/mm²; f_ctm=3,6 N/mm²)

Folgende Lasten sind anzusetzen:

EigenlastFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad\qquad}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_k=25\frac{kN}{m}}
Ausbaulast	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_k=3,75\frac{kN}{m}}
Verkehrslast (Gleichlast)	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_k=12\frac{kN}{m}}
Verkehrslast (Einzellast)	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{qk}=300kN}

Die Einzellasten werden als Wanderlast angesetzt.

Temperaturlasten und statisch unbestimmte Vorspannmomente sind wegen des statischen Systems nicht zu berücksichtigen.

Materialkennwerte

f_ck=33 N/mm²=3,3 kN/cm²

f_ctm=3,6 N/mm²=0,36 kN/cm²

f_yk=550 N/mm²=55 kN/cm²

f_pk=1370 N/mm²=137 kN/cm²

Querschnittswerte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_b=b\cdot h=100\cdot100=10000cm^2}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_I=\frac{b\cdot h^3}{12}=\frac{100\cdot 100^3}{12}=8333333cm^4}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_b=\frac{I_I}{z}=\frac{8333333}{50}=166666cm^3}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_{bz}=35cm}

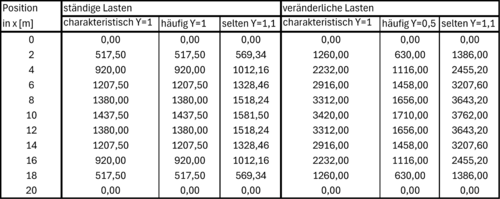
Schnittgrößenermittlung

ständige Lasten:

charakteristischFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad\qquad}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_k=25+3,75=28,75\frac{kN}{m}}
häufig	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{d,frequ}=25+3,75=28,75\frac{kN}{m}}
selten	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g_{d,inf}=(25+3,75)\cdot1,1=31,63\frac{kN}{m}}

veränderliche Lasten:

Gleichlasten:

charakteristischFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad\qquad}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_k=12\frac{kN}{m}}
häufig	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{d,frequ}=12\cdot0,5=6\frac{kN}{m}}
selten	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_{d,inf}=12\cdot1,1=13,2\frac{kN}{m}}

Einzellasten:

charakteristischFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \qquad\qquad\qquad}	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{qk}=300kN}
häufig	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{qd,frequ}=300\cdot0,5=150kN}
selten	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{qd,inf}=300\cdot1,1=330kN}

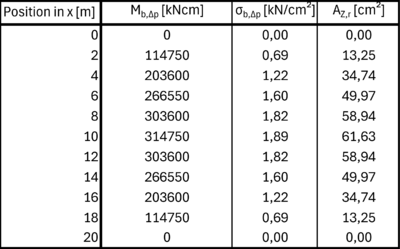
Momente in den Nachweisquerschnitten [kNm]

Nachweis

Der Nachweis wird in den Zehntelspunkten des Trägers geführt, sodass sich 11 Nachweisquerschnitte ergeben.

Der Nachweis wird im Folgenden nur für den Nachweisquerschnitt in Bauteilmitte ausführlich dargestellt. Die Darstellung der Ergebnisse der übrigen Schnitte findet tabellarisch statt.

Ermittlung der Restspannstahlfläche

Die Betonspannung am gezogenen Rand kann vor der Rissbildung linear-elastisch ermittelt werden:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{b,\Delta p}=\frac{M}{I_I}\cdot z_{I,c1}}

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \sigma _{b,\Delta p}={\frac {143750+171000}{8333333}}\cdot 50=1,89{\frac {kN}{cm^{2}}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon^{(0)}_{v,\infty}\cdot E_p=800\frac{N}{mm^2}=80\frac{kN}{cm^2}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{Z,r}=\frac{\sigma_{b,\Delta p}-f_{ctm}+\frac{M_{VX,\infty}}{W_b}+\frac{M_{\Delta T,freq}}{W_b}}{\varepsilon^{(0)}_{v,\infty}\cdot E_p\cdot\left(\frac{1}{A_b}+\frac{y_{bz}}{W_b}\right)}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{Z,r}=\frac{1,89-0,36}{80\cdot\left(\frac{1}{10000}+\frac{35}{166666}\right)}=61,69cm^2}

Ermittlung der Bruchsicherheit

Zunächst ist das Tragmoment der Bewehrung zu ermitteln. Hierbei sind gemäß der Handlungsanweisung Spannungsrisskorrosion die charakteristischen Materialkennwerte zu verwenden. In diesem Beispiel wird davon ausgegangen, dass die volle Festigkeit der Bewehrung aktiviert wird.

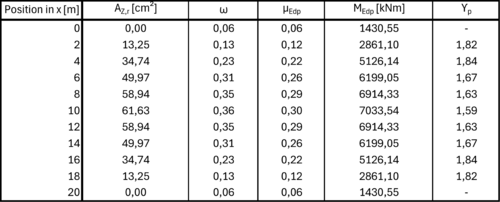
Die Tragfähigkeit wird mit den ω-Tafeln ermittelt.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega=\frac{A_{Z,r}\cdot f_{pd}+A_s\cdot f_{sd}}{b\cdot d_p\cdot f_{cd}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega=\frac{61,69\cdot 137+31,42\cdot 55}{100\cdot 85\cdot 3,3}=0,363}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_{Edp}=0,295}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Edp}=\mu_{Edp}\cdot b\cdot d^2\cdot f_{cd}=0,295\cdot100\cdot 85^2\cdot3,3}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Edp}=703354 kNcm=7033,54 kNm}

Die Bruchsicherheit ergibt sich anschließend wie folgt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_P=\frac{M_{AZ,r}+M_{As}-M_{\Delta T}-M_{VX,\infty}-\gamma_g\cdot M_g}{M_q}\geq1,1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_P=\frac{7033,54-1581,5}{3420}=1,59}

Nachweis

In Bauteilmitte ist der Nachweis erfüllt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\underline{\gamma_{p,vorh}=1,59\geq1,1=\gamma_{p,erf}}}}

Auch in den Übrigen Querschnitten ist der Nachweis erfüllt. Dies ist vor allem auf die vorhandene schlaffe Bewehrung zurückzuführen.

Seiteninfo Status: Seite fertig, ungeprüft