Querkraftbemessung - Bauteile ohne rechnerisch erforderliche Querkraftbewehrung

Bogen-Zugband-Modell bei Belastung durch eine Gleichstreckenlast

Aufgrund der äußerst komplexen Vorgänge beim Biegeschubversagen ist es bislang nicht gelungen, ein allgemein anerkanntes und mechanisch begründetes Tragmodell zu entwickeln. Es existiert eine Vielzahl mechanischer Modelle, die Teilaspekte des Tragverhaltens abbilden, jedoch führen deren Kombinationen häufig zu widersprüchlichen Ansätzen. Aus diesem Grund wurden empirische Modelle entwickelt, die auf umfangreichen Versuchsreihen und Beobachtungen basieren. Auch das aktuell gültige Regelwerk (EC2, Teil 1-1) stützt sich auf diese empirischen Ansätze.

Tragmodell

Kraftfluss innerhalb des Zahnmodells (einzelner Betonzahn)

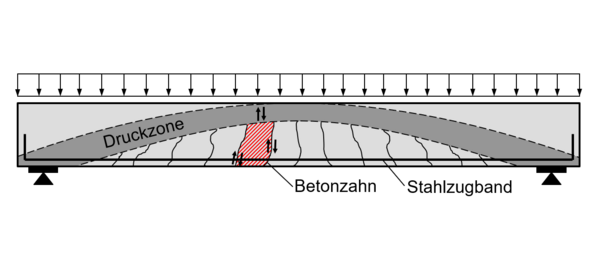
Ein bedeutender Tragmechanismus für Bauteile ohne rechnerisch erforderliche Querkraftbewehrung ist die Kombination aus dem Bogen-Zugband-Modell und dem Kamm- bzw. Zahnmodell. Bei Belastung durch eine Einzellast bildet sich ein Sprengwerk, bei Flächenlasten ein parabelförmiger Druckbogen aus. Dieser erzeugt Horizontalkräfte an den Auflagern, die über die Längsbewehrung als Zugband aufgenommen werden. Unterhalb des Druckbogens werden weitere Tragmechanismen aktiviert, die durch das Zahnmodell beschrieben werden. Es entstehen sogenannte Betonzähne, die durch idealisierte Biegeschubrisse begrenzt sind und kontinuierlich mit der Betondruckzone (Druckbogen) verbunden bleiben. Dadurch besteht eine ständige Verbindung zwischen Druck- und Zuggurt, über die die Zugkräfte aus der Bewehrung abgebaut werden können.

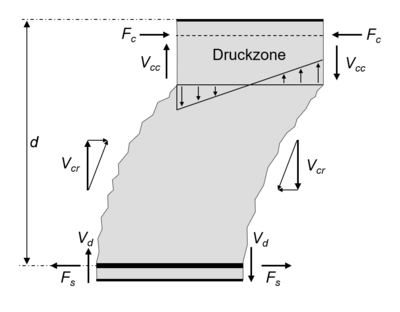
In diesem Modell wird die Querkraft durch folgende Traganteile abgetragen – jeweils mit den entsprechenden Einflussfaktoren:

• Querkrafttraganteil der Druckzone $V_{\mathrm {cc} }$: Da sich der Beton in der Druckzone im Zustand I befindet (ungerissen), kann er einen Teil der Querkraft abtragen.
  • Betonfestigkeit: Mit steigender Festigkeit können höhere Schubspannungen aufgenommen und somit größere Querkräfte abgetragen werden.
  • Bauteilquerschnitt: Je breiter der Querschnitt, desto breiter der Druckbogen – und damit kann eine größere Querkraft aufgenommen werden.
  • Längskräfte: Bei vorhandenen Druckkräften vergrößert sich die überdrückte Zone im Querschnitt, wodurch der Druckbogen breiter wird und höhere Schubkräfte übertragen werden können.
• Dübelwirkung der Längsbewehrung $V_{\mathrm {d} }$: Die Biegezugbewehrung verbindet benachbarte Betonzähne miteinander und ermöglicht so über Zugspannungen im Beton die Übertragung von Querkräften.
  • Bewehrungsquerschnitt: Je größer der Querschnitt der Längsbewehrung, desto höhere Querkräfte können über die Dübelwirkung übertragen werden.
  • Betondeckung: Ist die Betondeckung zu gering, kann der Beton abplatzen, wodurch die Querkräfte nicht mehr über die Dübelwirkung abgetragen werden können.
• Rissverzahnung $V_{\mathrm {cr} }$: Durch die Relativverschiebung zweier gegenüberliegender Rissufer entstehen Rissverzahnungsspannungen, die einen Teil der Querkraft aufnehmen können.
  • Betonzugfestigkeit: Eine höhere Zugfestigkeit des Betons führt zu kleineren Rissöffnungen, wodurch größere Rissverzahnungsspannungen entstehen und somit höhere Querkräfte aufgenommen werden können.
  • Längskräfte: Axiale Druckkräfte reduzieren die Rissbreite und ermöglichen dadurch eine größere Übertragung der Querkraft über die Rissverzahnung.
• Einspannwirkung der Betonzähne: Durch die Verformung des Bauteils entstehen Biegespannungen an der Einspannstelle der Betonzähne, die zur Aufnahme von Querkräften beitragen.
  • Betonfestigkeit: Mit höherer Betonfestigkeit können größere Biegespannungen an der Einspannstelle entstehen, wodurch ein höherer Querkraftwiderstand möglich ist.

Bemessung

Da das Versagen eines Bauteils ohne Querkraftbewehrung in der Regel durch die Ausbildung eines kritischen Schubrisses initiiert wird, ist im Rahmen der Bemessung nachzuweisen, dass die vorhandenen Beanspruchungen die maßgebende Schubrisslast nicht überschreiten. Hierzu wird gemäß Eurocode der Nachweis für gerissene Trägerstege herangezogen. Dieser basiert, mangels eines allgemein anerkannten Versagensmodells, auf semi-empirischen Ansätzen.

Nachweis für gerissene Trägerstege

Beispiel für die anrechenbare Längsbewehrung A_sl

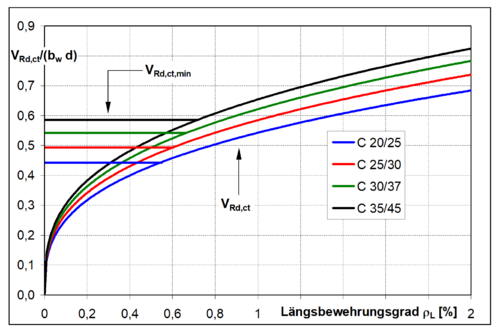
Die Gleichung ist nicht dimensionsrein, da beispielsweise aus der Betondruckfestigkeit $f_{\mathrm {ck} }$ die dritte Wurzel gezogen wird. Für ein korrektes Ergebnis empfiehlt es sich, alle Werte in den Einheiten [N], [mm] und [N/mm²] einzusetzen. Bei Versuchen wurde festgestellt, dass die Querkrafttragfähigkeit nur unterproportional mit der statischen Nutzhöhe $d$ ansteigt. Aus diesem Grund wurde der sogenannte Maßstabsfaktor $k$ in den Nachweis integriert. Um zu vermeiden, dass überbewehrte Bauteile mit sprödem Bruchverhalten geplant werden, ist der Längsbewehrungsgrad $\rho _{\mathrm {l} }$ auf 2 % begrenzt.

${\begin{aligned}\ V_{\mathrm {Rd,c} }=\left[C_{\mathrm {Rd,c} }\cdot k\cdot {\left(100\cdot \rho _{\mathrm {l} }\cdot f_{\mathrm {ck} }\right)}^{\frac {1}{3}}+0,12\cdot \sigma _{\mathrm {cp} }\right]\cdot b_{\mathrm {w} }\cdot d\geq V_{\mathrm {Rd,c,\min } }\end{aligned}}$

mit:

${\begin{aligned}\ C_{\mathrm {Rd,c} }={\frac {0,15}{\gamma _{\mathrm {c} }}}\end{aligned}}$ → Kalibrierfaktor

${\begin{aligned}\ k=1+{\sqrt {\frac {200}{d}}}\leq 2,0\end{aligned}}$ → Beiwert zur Berücksichtigung der Bauteilhöhe (Maßstabseffekt)

${\begin{aligned}\ \rho _{\mathrm {l} }={\frac {A_{\mathrm {sl} }}{b_{\mathrm {w} }\cdot d}}\leq 0,02\end{aligned}}$ → geometrischer Bewehrungsgrad der Längsbewehrung

${\begin{aligned}\ \sigma _{\mathrm {cp} }={\frac {N_{\mathrm {Ed} }}{A_{\mathrm {c} }}}<0,2\cdot f_{\mathrm {cd} }\end{aligned}}$ → einwirkende Längsspannungen

wobei:

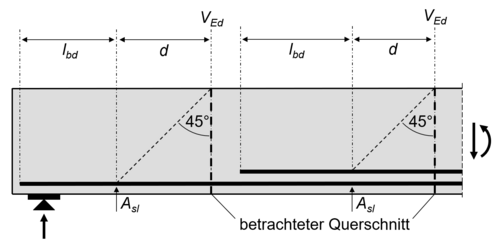
γc ...	der Teilsicherheitsbeiwert (= 1,5 bei ständiger und vorübergehender Bemessungssituation)
d ...	die statische Nutzhöhe
Asl ...	die Fläche der Zugbewehrung, die mindestens (lbd + d) über den betrachteten Querschnitt hinaus geführt wird (siehe Abb.)
lbd ...	die Verankerungslänge
bw ...	die kleinste Querschnittsbreite innerhalb der Zugzone des Querschnitts
fck ...	die charakteristische Betonfestigkeit
NEd ...	die Normalkraft im Querschnitt infolge Lastbeanspruchung (Druck ist positiv einzusetzen und Zug negativ)
Ac ...	die Betonquerschnittsfläche
fcd ...	der Bemessungswert der Betondruckfestigkeit

Mindestquerkrafttragfähigkeit

bezogene Querkrafttragfähigkeit bei reiner Biegung und d ≤ 200 mm

Da der Längsbewehrungsgrad $\rho _{\mathrm {l} }$ über eine Multiplikation in der Nachweisgleichung verankert ist, ergibt sich für Bauteile ohne Längsbewehrung formal keine Querkrafttragfähigkeit. In der Realität weisen solche Bauteile jedoch dennoch eine gewisse Querkrafttragfähigkeit auf, solange der Beton ungerissen bleibt. Um diese Bauteile nicht zu unterschätzen, wurde eine weitere empirische Formel entwickelt, welche die untere Grenze der Querkrafttragfähigkeit beschreibt und unabhängig vom Längsbewehrungsgrad berechnet wird.
Versuche haben gezeigt, dass die Querkrafttragfähigkeit mit zunehmender statischer Nutzhöhe sowie bei niedrigeren Bewehrungsgraden abnimmt. Aus diesem Grund wird über den Beiwert $\kappa _{\mathrm {1} }$ die Mindestquerkrafttragfähigkeit für Bauteile mit einer statischen Nutzhöhe von über 80 cm um etwa 30 % gegenüber dünneren Bauteilen (d ≤ 60 cm) reduziert.

${\begin{aligned}\ V_{\mathrm {Rd,c,\min } }=\left[{\frac {\kappa _{\mathrm {1} }}{\gamma _{\mathrm {c} }}}\cdot {\sqrt {{k}^{3}\cdot f_{\mathrm {ck} }}}+0,12\cdot \sigma _{\mathrm {cp} }\right]\cdot b_{\mathrm {w} }\cdot d\end{aligned}}$

wobei:

κ1 = 0,0525 für d ≤ 60cm

κ1 = 0,0375 für d > 80cm (Zwischenwerte sind zu interpolieren)

zusätzlicher Nachweis für auflagernahe Lasten

Der Nachweis für die Querkrafttragfähigkeit ohne Schubbewehrung darf auch bei auflagernahen Lasten verwendet werden, wenn ein zusätzlicher Nachweis der schrägen Betondruckstrebe geführt wird. Die Begrenzung der Druckstrebentragfähigkeit nach Gleichung wird in der Regel nur bei sehr großen auflagernahen Einzellasten maßgebend. Hierbei muss die einwirkende Querkraft ohne Abminderung ($\beta$ siehe Querkraftbemessung - Einwirkung) folgenden Bedingung erfüllen:

${\begin{aligned}\ V_{\mathrm {Ed} }=0,5\cdot b_{\mathrm {w} }\cdot d\cdot \nu \cdot f_{\mathrm {cd} }\end{aligned}}$

wobei:

ν = 0,675 → Abminderungsbeiwert für die Betonfestigkeit bei Schubrissen

Schubtal nach KANI

Ein belastetes Bauteil kann ein Querkraftversagen erleiden, noch bevor die Biegetragfähigkeit erreicht wird. Die Querkraft- und Biegetragfähigkeit werden in getrennten Nachweisen erfasst, beruhen jedoch in weiten Teilen auf denselben Parametern (z. B. Längsbewehrungsgrad $\rho _{\mathrm {l} }$, Betondruckfestigkeit $f_{\mathrm {ck} }$, Bauteilabmessungen etc.). Daraus ergibt sich eine direkte Wechselwirkung zwischen den jeweiligen Versagenslasten.
Um zu bestimmen, ob die Biegetragfähigkeit des Querschnitts $M_{\mathrm {Rd} }$ oder das beim Querkraftversagen erreichte maximale Moment $M_{\mathrm {uV} }$ maßgebend ist, wird der Quotient aus diesen beiden Momenten gebildet.

${\begin{aligned}\ {\frac {M_{\mathrm {uV} }}{M_{\mathrm {Rd} }}}>1.0\end{aligned}}$ → Biegeversagen

${\begin{aligned}\ {\frac {M_{\mathrm {uV} }}{M_{\mathrm {Rd} }}}<1.0\end{aligned}}$ → Querkraftversagen

wobei:

MRd ...	maximal aufnehmbares Moment bei der Biegebemessung des Querschnitts
MuV ...	das beim Querkraftversagen erreichte maximale Moment

Stellt man die Berechnungsergebnisse für einen Rechteckquerschnitt unter Berücksichtigung der Schubschlankheit $\lambda$ (das geometrische Verhältnis des Abstandes zwischen Einzellast und Auflagerlinie zur statischen Nutzhöhe $d$) und des Bewehrungsgrads $\rho _{\mathrm {l} }$ in einem dreidimensionalen Diagramm dar, entsteht ein Tal, in dem der Quotient kleiner als 1,0 ist – die Querkrafttragfähigkeit wird somit maßgebend. Dieses sogenannte „Schubtal“ geht auf Kani zurück. Im Schubtal kann die Biegezugbewehrung nicht vollständig ausgenutzt werden, und der Querschnitt würde auf Schub versagen.

Um ein vorzeitiges Versagen des Bauteils zu verhindern, muss in solchen Fällen eine Querkraftbewehrung vorgesehen werden, die das „Schubtal“ überwindet und es ermöglicht, die rechnerische Biegetragfähigkeit tatsächlich zu erreichen. Für schubschlanke, gering bewehrte Bauteile – wie beispielsweise Deckenplatten im Hochbau – ist der Quotient in der Regel größer als 1,0, sodass die Querkrafttragfähigkeit ausreichend ist.

Versagensarten

Bei Bauteilen ohne Querkraftbewehrung können infolge der Querkraftbeanspruchung folgende Versagensmechanismen auftreten:

• Biegeschubversagen

Bei steigender Belastung entsteht im Balken ein Biegeschubriss, der sich in Höhe der Dehnungsnulllinie in Richtung der Last­einleitung bewegt und gleichzeitig in entgegengesetzter Richtung entlang der Längsbewehrung auf das Auflager zuschreitet. Dieser sogenannte kritische Schubriss trennt den Druck- vom Zuggurt, wodurch sich die inneren Kräfte zu einem Sprengwerk umlagern. Mit zunehmender Belastung wächst der Riss weiter in die Druckzone hinein, bis die verbleibende Druckzone die auftretenden Beanspruchungen nicht mehr aufnehmen kann – der Querschnitt versagt dann schlagartig. Das eigentliche Versagen wird primär durch das Fortschreiten des Biegeschubrisses verursacht, während der Bruch der Druckzone lediglich als Folgeerscheinung auftritt.

• Stegzugversagen

• Verankerungsversagen

Quellen

Seiteninfo Status: Seite in Bearbeitung