Kraftfluss innerhalb eines Querkraftbewehrten Trägers (Fachwerkmodell)

Da ein belastetes Bauteil ohne Querkraftbewehrung ein Querkraftversagen erleiden kann, noch bevor die Biegetragfähigkeit erreicht ist (siehe Schubtal nach KANI), muss der Querschnitt in solchen Fällen mit Querkraftbewehrung versehen werden. Durch eine Bewehrung, die die entstehenden Risse kreuzt, wird es möglich, die rechnerisch ansetzbare Biegetragfähigkeit tatsächlich zu erreichen. Durch die zusätzliche Verstärkung entsteht die zentrale Modellvorstellung des Kraftflusses bei querkraftbewehrten Bauteilen: das Fachwerkmodell. ^[1]

Tragmodell

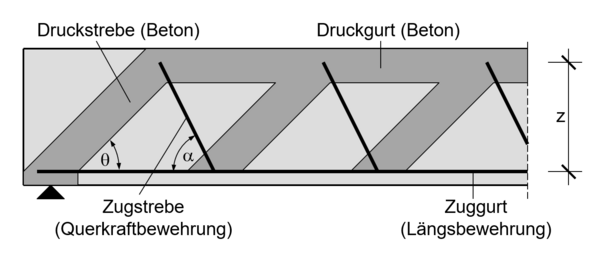
Der Kraftfluss eines Bauteils, das sowohl auf Biegung als auch auf Querkraft beansprucht wird, lässt sich am anschaulichsten durch ein Stabwerkmodell darstellen. Das klassische Fachwerkmodell besteht aus einem Betondruckgurt sowie einem Zuggurt, der durch die Biegezugbewehrung gebildet wird. Beide Gurte verlaufen parallel zueinander entlang der Balkenränder. Die Druckdiagonalen (Betondruckstreben) verlaufen unter dem Winkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta} , der im Rahmen normativer Vorgaben (nach EC2) frei gewählt werden darf. Die Zugdiagonalen (Querkraftbewehrung) sind unter dem Winkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} zwischen 45° und 90° zur Trägerachse geneigt. ^[1] ^[2]

Bemessung

Begrenzung des Druckstrebenwinkels Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta}

Mit der folgenden Gleichung wird der flachstmögliche Druckstrebenwinkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta_\mathrm{\min}} (entspricht dem maximalen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cot \theta} ) ermittelt, der zur minimal erforderlichen Querkraftbewehrung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{sw,erf}} führt. Der Druckstrebenwinkel darf jedoch zwischen dem berechneten Minimalwert und 45° bzw. 60° bei geneigten Bügeln frei gewählt werden. Der Querkraftanteil (Betontraganteil) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,cc}} kann als Vertikalkomponente der Reibungskräfte in einem Schrägriss gedeutet werden. Steigt der Längsdruck an, so reduziert sich der Querkraftanteil Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,cc}} , da flachere Rissneigungen zu einer geringeren vertikalen Kraftkomponente entlang der Rissflächen führen. ^[3]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ 1,0 \leq \cot \theta \leq \frac{1,2 + 1,4 \frac{\sigma_\mathrm{cp}}{f_\mathrm{cd}}}{1 - \frac{V_\mathrm{Rd,cc}}{V_\mathrm{Ed}}} \leq 3,0 \end{align} \quad } → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad {45}^{\circ} \leq \theta \leq {18,44}^{\circ} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ V_\mathrm{Rd,cc} = 0,5 \cdot 0,48 \cdot {f_\mathrm{ck}}^{\frac{1}{3}} \cdot \left( 1 - 1,2 \frac{\sigma_\mathrm{cp}}{f_\mathrm{cd}} \right) \cdot b_\mathrm{w} \cdot z \end{align}}

wobei:

cot ...	Kotangens (1 / tanθ)
θ ...	der Winkel zwischen Betondruckstreben und der rechtwinklig zur Querkraft verlaufenden Bauteilachse
σ_cp ...	der Bemessungswert der Betonlängsspannung in Höhe des Schwerpunkts des Querschnitts σ_cp = N_Ed / A_c Betondruckspannungen sind positiv definiert
N_Ed ...	die Normalkraft im Querschnitt infolge Lastbeanspruchung (Druck ist positiv einzusetzen und Zug negativ)
f_cd ...	der Bemessungswert der Betondruckfestigkeit
V_Rd,cc ...	der Querkraftanteil des Betonquerschnitts mit Querkraftbewehrung
V_Ed ...	der Bemessungswert der einwirkenden Querkraft
f_ck ...	die charakteristische Betonfestigkeit
b_w ...	die kleinste Querschnittsbreite innerhalb der Zugzone des Querschnitts
z ...	der innerer Hebelarm (0,9d)

Bei geneigter Querkraftbewehrung darf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cot\theta} bis 0,58 (60°) ausgenutzt werden. Vereinfachend dürfen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cot\theta} die folgenden Werte angesetzt werden:

reine Biegung: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad \quad \quad \quad \quad \quad \cot\theta = 1,2 \quad } → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad \theta = {39,81}^{\circ} }
Biegung und Längsdruckkraft:Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad \cot\theta = 1,2 \quad } → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad \theta = {39,81}^{\circ} }
Biegung und Längszugkraft: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad \cot\theta = 1,0 \quad } → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \quad \theta = {45}^{\circ} }

Bemessung des Querkraftwiderstands Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd}}

Der Querkraftwiderstand von Bauteilen mit Querkraftbewehrung hängt von zwei Komponenten ab: dem Widerstand der Betondruckstrebe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,\max}} und dem Widerstand der Querkraftbewehrung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,s}} . Beide Größen lassen sich aus dem Gelenkfachwerkmodell unter Berücksichtigung der Gleichgewichtsbedingungen ableiten und bilden die Grundlage für den Querkraftnachweis bei Bauteilen mit rechnerisch erforderlicher Querkraftbewehrung. ^[1] ^[3]

Dabei ist zwischen der vereinfachten Formel für lotrechte Bügel und der vollständigen Gleichung für geneigte Querkraftbewehrungen zu unterscheiden. Maßgebend ist stets der kleinere der beiden Widerstände (Betondruckstrebe oder Querkraftbewehrung), der größer sein muss als die einwirkende Querkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed}} , damit der Nachweis erfüllt ist. ^[3]

lotrechte Querkraftbewehrung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ V_\mathrm{Rd,s} = a_\mathrm{sw} \cdot z \cdot f_\mathrm{yd} \cdot \cot \theta \quad \end{align}} → Widerstand der Querkraftbewehrung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ V_\mathrm{Rd,\max} = \frac{b_\mathrm{w} \cdot z \cdot \nu_\mathrm{1} \cdot f_\mathrm{cd}}{\cot \theta + tan \theta} \quad \end{align}} → Widerstand der Betondruckstrebe

geneigte Querkraftbewehrung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ V_\mathrm{Rd,s} = a_\mathrm{sw} \cdot z \cdot f_\mathrm{yd} \cdot \left( \cot \theta + \cot \alpha \right) \cdot \sin \alpha \quad \end{align}} → Widerstand der Querkraftbewehrung

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\begin{aligned}\ V_{\mathrm {Rd,\max } }={\frac {b_{\mathrm {w} }\cdot z\cdot \nu _{\mathrm {1} }\cdot f_{\mathrm {cd} }\cdot \left(\cot \theta +\cot \alpha \right)}{1+{\cot }^{2}\theta }}\quad \end{aligned}}} → Widerstand der Betondruckstrebe

wobei:

a_sw ...	die Bewehrungsmenge je Längeneinheit a_sw = A_sw / s_w
A_sw ...	die Querschnittsfläche der Querkraftbewehrung
s_w ...	der Bügelabstand
z ...	der innerer Hebelarm (0,9d)
f_yd ...	der Bemessungswert der Streckgrenze der Querkraftbewehrung
cot ...	Kotangens (1 / tanθ)
θ ...	Winkel zwischen Betondruckstreben und der rechtwinklig zur Querkraft verlaufenden Bauteilachse
b_w ...	die kleinste Querschnittsbreite innerhalb der Zugzone des Querschnitts
ν₁ ...	ein Abminderungsbeiwert für die Betonfestigkeit infolge schiefwinklig kreuzender Risse ν₁ = 0,75 für ≤ C50/60
f_cd ...	der Bemessungswert der Betondruckfestigkeit
α ...	der Winkel zwischen Querkraftbewehrung und der rechtwinklig zur Querkraft verlaufenden Bauteilachse

Im GZT kann durch Gleichsetzen der einwirkenden Querkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed}} mit dem Widerstand der Querkraftbewehrung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,s}} und anschließendes Umstellen der Nachweisformel die erforderliche Querkraftbewehrung berechnet werden.

lotrechte Querkraftbewehrung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ a_\mathrm{sw} = \frac{V_\mathrm{Ed}}{z \cdot f_\mathrm{yd} \cdot \cot \theta} \end{align}}

geneigte Querkraftbewehrung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \ a_\mathrm{sw} = \frac{V_\mathrm{Ed}}{z \cdot f_\mathrm{yd} \cdot \left( \cot \theta + \cot \alpha \right) \cdot \sin \alpha} \end{align}}

Versagensarten

Arten der Querkraftbewehrung

konstruktive Regeln

Quellen

↑ ^1,0 ^1,1 ^1,2 ZILCH, KONRAD und ZEHETMAIER, GERHARD: Bemessung im konstruktiven Betonbau, Springer-Verlag Berlin Heidelberg, 2010
↑ BOLLE, GUIDO: Querkraftbemessung bei Bauteilen ohne Querkraftbewehrung, Stahlbetonbau I, Hochschule Wismar, Skript, TK 8, 2022
↑ ^3,0 ^3,1 ^3,2 FINGERLOOS, FRANK; HEEGER, JOSEF und ZILCH, KONRAD: Eurocode 2 für Deutschland - Kommentierte Fassung, Beuth Verlag GmbH, 2016

Seiteninfo

Status: Seite in Bearbeitung

[Zilch-1] 1,0 ^1,1 ^1,2 ZILCH, KONRAD und ZEHETMAIER, GERHARD: Bemessung im konstruktiven Betonbau, Springer-Verlag Berlin Heidelberg, 2010

[Bolle-2] BOLLE, GUIDO: Querkraftbemessung bei Bauteilen ohne Querkraftbewehrung, Stahlbetonbau I, Hochschule Wismar, Skript, TK 8, 2022

[EC2-3] 3,0 ^3,1 ^3,2 FINGERLOOS, FRANK; HEEGER, JOSEF und ZILCH, KONRAD: Eurocode 2 für Deutschland - Kommentierte Fassung, Beuth Verlag GmbH, 2016

[1]

[2]

[3]

Querkraftbemessung - Bauteile mit rechnerisch erforderlicher Querkraftbewehrung

Inhaltsverzeichnis