Zwang - verringerte Zwangsbeanspruchungen: Unterschied zwischen den Versionen
| (23 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Allgemeines == | == Allgemeines == | ||
| − | Die in diesem Abschnitt behandelten Berechnungsverfahren zur Ermittlung der Zwangsschnittgrößen in Sohlplatten und Wänden gelten als Empfehlung, die im „Lohmeyer Stahlbetonbau“ <ref name = " | + | Die in diesem Abschnitt behandelten Berechnungsverfahren zur Ermittlung der Zwangsschnittgrößen in Sohlplatten und Wänden gelten als Empfehlung, die im „Lohmeyer Stahlbetonbau“ <ref name = "Q1"> Baar, S.; Ebeling, K.: Lohmeyer Stahlbetonbau. Bemessung-Konstruktion-Ausführung. 10.Auflage. Wiesbaden 2017 </ref> gegeben wird und stellen eine Ergänzung zu der in der DIN EN 1992-1-1 <ref name = "Q2"> DIN EN 1992-1-1 Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau mit Nationalem Anhang. Beuth Verlag GmbH 2016 </ref> angegebenen [[Zwang - Mindestbewehrung zur Rissbreitenbegrenzung | Ermittlung der rissbreitenbegrenzenden Bewehrung]] dar. |
== <span id="verminderter Zwang in Sohlplatten"></span> verminderter Zwang in Sohlplatten == | == <span id="verminderter Zwang in Sohlplatten"></span> verminderter Zwang in Sohlplatten == | ||
| − | Kann eine Beanspruchung aus spätem Zwang, z.B. während der Bauphase oder des Nutzungszeitraumes, ausgeschlossen werden, darf der Nachweis für den frühen Zwang aus dem Abfließen der Hydratationswärme geführt werden. Zusätzlich dazu kann die | + | Kann eine Beanspruchung aus spätem Zwang, z.B. während der Bauphase oder des Nutzungszeitraumes, ausgeschlossen werden, darf der Nachweis für den frühen Zwang aus dem Abfließen der Hydratationswärme geführt werden. Zusätzlich dazu kann die Zwangsspannung vermindert werden, wenn in der Sohlplatte keine anderen Zwangsbeanspruchungen wirken und die Sohlplattenbewegungen nicht durch Festpunkte behindert werden. |
Die rechnerische Zugspannung in der Sohlplatte σ<sub>ct,d</sub> ist abhängig vom Reibungsbeiwert μ<sub>d</sub>, der Spannung σ<sub>0</sub> und der Länge L der verschiebbaren Sohlplatte. | Die rechnerische Zugspannung in der Sohlplatte σ<sub>ct,d</sub> ist abhängig vom Reibungsbeiwert μ<sub>d</sub>, der Spannung σ<sub>0</sub> und der Länge L der verschiebbaren Sohlplatte. | ||
:: <math> \sigma_{ct,d} = \cfrac{\gamma_{ct} \cdot \mu_d \cdot \sigma_0 \cdot L}{2 \cdot a_{ct}} </math> | :: <math> \sigma_{ct,d} = \cfrac{\gamma_{ct} \cdot \mu_d \cdot \sigma_0 \cdot L}{2 \cdot a_{ct}} </math> | ||
| Zeile 10: | Zeile 10: | ||
| <math> \sigma_{ct,d} </math> || Bemessungswert der wirksamen Betonzugspannung, die durch die Reibung auf dem Untergrund entsteht, wenn sich die Sohlplatte verkürzt | | <math> \sigma_{ct,d} </math> || Bemessungswert der wirksamen Betonzugspannung, die durch die Reibung auf dem Untergrund entsteht, wenn sich die Sohlplatte verkürzt | ||
|- | |- | ||
| − | |<math> \gamma_{ct} </math> || | + | |<math> \gamma_{ct} </math> || Sicherheitsbeiwert im Grenzzustand der Gebrauchstauglichkeit |
|- | |- | ||
| || γ<sub>ct</sub> = 1,0 wenn die Zwangsspannung durch das Abfließen der Hydratationswärme hervorgerufen wird | | || γ<sub>ct</sub> = 1,0 wenn die Zwangsspannung durch das Abfließen der Hydratationswärme hervorgerufen wird | ||
|- | |- | ||
| − | | <math> \mu_d </math> || Bemessungswert des | + | | <math> \mu_d </math> || Bemessungswert des Reibungsbeiwertes |
|- | |- | ||
| <math> \cfrac{L}{2} </math> || Reibungslänge der Sohlplatte | | <math> \cfrac{L}{2} </math> || Reibungslänge der Sohlplatte | ||
| Zeile 25: | Zeile 25: | ||
|} | |} | ||
| − | Reibungsbeiwerte für unterschiedliche Untergründe sind in der folgenden Tabelle aufgelistet. Ein Reibungsbeiwert darf nur bei | + | Reibungsbeiwerte für unterschiedliche Untergründe sind in der folgenden Tabelle aufgelistet. Ein Reibungsbeiwert darf nur bei Sohlplatten mit ebener Unterseite angesetzt werden, die sich auf dem Untergrund frei bewegen können und deren Verformungen nicht durch Fundamentvertiefungen, wie z.B. bei Aufzugschächten behindert werden. <ref name = "Q1"> </ref> |
{| class="wikitable" style="margin: auto;" | {| class="wikitable" style="margin: auto;" | ||
| − | |+style="text-align: left;" | Reibungsbeiwerte <ref name = " | + | |+style="text-align: left;" | Reibungsbeiwerte <ref name = "Q1"> </ref> <ref name = "Q3"> Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 9. überarbeitete und erweiterte Auflage. Düsseldorf 2009 </ref> <ref name = "Q4"> Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 11. überarbeitete Auflage. Düsseldorf 2018 </ref> |
|- | |- | ||
|rowspan="2"| | |rowspan="2"| | ||
| Zeile 67: | Zeile 67: | ||
|- | |- | ||
|7 | |7 | ||
| − | |Sandbett (Dicke 6 … | + | |Sandbett (Dicke 6 … 10cm, mittlere Korngröße 0,35mm) |
|keine (Direktauflagerung auf nicht feinkörnigem, bindigem Boden) | |keine (Direktauflagerung auf nicht feinkörnigem, bindigem Boden) | ||
|style="text-align: center;" | 0,7 | |style="text-align: center;" | 0,7 | ||
| Zeile 136: | Zeile 136: | ||
|23 | |23 | ||
|rowspan="2"| Sicherheitsbeiwert für Reibung <sup>h)</sup> | |rowspan="2"| Sicherheitsbeiwert für Reibung <sup>h)</sup> | ||
| − | |colspan="2" style="text-align: center;" | | + | |colspan="2" style="text-align: center;" | γ<sub>R</sub> = 1,35 <sup>f)</sup> |
|- | |- | ||
|24 | |24 | ||
| − | |colspan="2" style="text-align: center;" | | + | |colspan="2" style="text-align: center;" |γ<sub>R</sub> =1,25 <sup>g)</sup> |
|- | |- | ||
|25 | |25 | ||
|Bemessungswert der Reibung | |Bemessungswert der Reibung | ||
| − | |colspan="2" style="text-align: center;" |<math> \mu_d = \ | + | |colspan="2" style="text-align: center;" |<math> \mu_d = \gamma_R \cdot \mu_0 </math> |
|- | |- | ||
| − | |colspan="4" | <sup>a)</sup> Die Oberfläche der Unterkonstruktion muss den Anforderungen der Ebenheit nach DIN 18202 entsprechen. | + | |colspan="4" | <sup>a)</sup> Die Oberfläche der Unterkonstruktion muss den Anforderungen der Ebenheit nach DIN 18202 entsprechen. <br/> |
| − | <sup>b)</sup> PE = Polyethylen, PTFE = | + | <sup>b)</sup> PE = Polyethylen, PTFE = Polytetrafluor- Ethylen<br/> |
| − | <sup>c)</sup> Bituminöse Trennschichten sind nur bei ausreichender Schichtdicke und Temperaturen in der Trennschicht >10°C wirksam. | + | <sup>c)</sup> Bituminöse Trennschichten sind nur bei ausreichender Schichtdicke und Temperaturen in der Trennschicht >10°C wirksam.<br/> |
| − | <sup>d)</sup> Vorschlag der Autoren der Fachliteraturquellen | + | <sup>d)</sup> Vorschlag der Autoren der Fachliteraturquellen<br/> |
| − | <sup>e)</sup> Bewegt sich der Reibungsbeiwert in einer Spannbreite empfehlen die Autoren der Fachliteraturquellen die Annahme des höheren Wertes, wenn kein Einfluss auf die Ausführung besteht. | + | <sup>e)</sup> Bewegt sich der Reibungsbeiwert in einer Spannbreite empfehlen die Autoren der Fachliteraturquellen die Annahme des höheren Wertes, wenn kein Einfluss auf die Ausführung besteht.<br/> |
| − | <sup>f)</sup> nach "Lohmeyer Stahlbetonbau" <ref name = " | + | <sup>f)</sup> nach "Lohmeyer Stahlbetonbau" <ref name = "Q1"> </ref> und "Weiße Wannen einfach und sicher - 9.Auflage" <ref name = "Q3"> </ref><br/> |
| − | <sup>g)</sup> nach "Weiße Wannen einfach und sicher - 11.Auflage"<ref name = " | + | <sup>g)</sup> nach "Weiße Wannen einfach und sicher - 11.Auflage"<ref name = "Q4"> </ref><br/> |
<sup>h)</sup> Die Autoren der Fachliteraturen empfehlen mit den angegebenen Sicherheitsbeiwerten zu rechnen, da die Auswahl des Reibungsbeiwertes mit einiger Unsicherheit behaftet ist. | <sup>h)</sup> Die Autoren der Fachliteraturen empfehlen mit den angegebenen Sicherheitsbeiwerten zu rechnen, da die Auswahl des Reibungsbeiwertes mit einiger Unsicherheit behaftet ist. | ||
| Zeile 163: | Zeile 163: | ||
== <span id="verminderter Zwang in Wänden"></span> verminderter Zwang in Wänden == | == <span id="verminderter Zwang in Wänden"></span> verminderter Zwang in Wänden == | ||
| − | Durch das nachträgliche Betonieren einer Wand auf eine Sohlplatte entstehen in der Wand Zwangsspannungen infolge der Verformungsbehinderung durch den Verbund beider Bauteile. Die ersten wesentlichen Zwangsbeanspruchungen treten in der Wand beim Abfließen der Hydratationswärme auf. <ref name = " | + | Durch das nachträgliche Betonieren einer Wand auf eine Sohlplatte entstehen in der Wand Zwangsspannungen infolge der Verformungsbehinderung durch den Verbund beider Bauteile. Die ersten wesentlichen Zwangsbeanspruchungen treten in der Wand beim Abfließen der Hydratationswärme auf. <ref name = "Q1"> </ref> <br/> |
| − | Wenn | + | Wenn der späte Zwang z.B. Temperaturänderungen im Tages- oder Jahreswechsel mit Sicherheit ausgeschlossen werden kann, darf die in der Wand entstehende Zwangsspannung wie folgt abgeschätzt werden. |
| − | :: <math> \sigma_{ct,cal} = k \cdot \alpha_T \cdot | + | :: <math> \sigma_{ct,cal} = k \cdot \alpha_T \cdot E_{c,t} \cdot \Delta T_{b,W-F} </math> |
:::{| | :::{| | ||
| <math> \sigma_{ct,cal} </math> || Rechenwert der Betonzugspannung, die infolge Zwangsspannungen durch das Abfließen der Hydratationswärme entsteht | | <math> \sigma_{ct,cal} </math> || Rechenwert der Betonzugspannung, die infolge Zwangsspannungen durch das Abfließen der Hydratationswärme entsteht | ||
|- | |- | ||
| − | | <math> k </math> || Beiwert die Behinderung der Verformungsmöglichkeit eines Bauteils | + | | <math> k </math> || Beiwert für die Behinderung der Verformungsmöglichkeit eines Bauteils |
|- | |- | ||
| − | | || k = 1,0 für Wände, die auf ein anderes Bauteil, z.B. eine Sohlplatte betoniert | + | | || k = 1,0 für Wände, die auf ein anderes Bauteil, z.B. eine Sohlplatte betoniert werden |
|- | |- | ||
| − | | <math> \alpha_T </math> || Temperaturausdehnungskoeffizient des | + | | <math> \alpha_T </math> || Temperaturausdehnungskoeffizient des Betons |
|- | |- | ||
| − | | || < | + | | || α<sub>T</sub> = 10 ∙ 10<sup>-6</sup> 1/K |
|- | |- | ||
| − | | <math> | + | | <math> E_{c,t} </math> || wirksamer Elastizitätsmodul des Betons zum Zeitpunkt t<sub>maxT</sub> der Entstehung der Betonzugspannungen |
|- | |- | ||
| − | | || < | + | | || E<sub>c,t</sub> = α<sub>E</sub> ∙ E<sub>cm</sub> |
|- | |- | ||
| − | | || < | + | | || t<sub>maxT</sub> = 1 + 0,8 ∙ h || h in m |
|- | |- | ||
| <math> \Delta T_{b,W-F} </math> || Temperaturdifferenz zwischen der mittleren Bauteiltemperatur der Wand und der Sohlplatte | | <math> \Delta T_{b,W-F} </math> || Temperaturdifferenz zwischen der mittleren Bauteiltemperatur der Wand und der Sohlplatte | ||
|} | |} | ||
| − | Anhand der folgenden Tabelle lässt sich der Verhältniswert α<sub>E</sub> der Elastizitätsmoduln ablesen. | + | Anhand der folgenden Tabelle lässt sich der Verhältniswert α<sub>E</sub> der Elastizitätsmoduln in Abhängigkeit des Bauteilalters t<sub>maxT</sub> bei Entstehung der Betonzugspannungen ablesen. |
{| class="wikitable" style="margin: auto;" | {| class="wikitable" style="margin: auto;" | ||
|+style="text-align: left;" | Verhältniswert α<sub>E</sub> | |+style="text-align: left;" | Verhältniswert α<sub>E</sub> | ||
| − | <ref name = " | + | <ref name = "Q1"> </ref> |
|- | |- | ||
|rowspan="2"| | |rowspan="2"| | ||
| Zeile 221: | Zeile 221: | ||
|} | |} | ||
| − | Die Temperaturdifferenz zwischen der mittleren Bauteiltemperatur der Wand und der Bauteiltemperatur der Sohlplatte bzw. des Fundamentes lässt sich wie folgt ermitteln.<ref name = " | + | Die Temperaturdifferenz zwischen der mittleren Bauteiltemperatur der Wand und der Bauteiltemperatur der Sohlplatte bzw. des Fundamentes lässt sich wie folgt ermitteln.<ref name = "Q1"> </ref> |
:: <math> \Delta T_{b,W-F} = T_{b,m} - T_F </math> | :: <math> \Delta T_{b,W-F} = T_{b,m} - T_F </math> | ||
| Zeile 236: | Zeile 236: | ||
| <math> k_{Tv} </math> || Beiwert zur Berücksichtigung des Temperaturverlaufs in der Wand | | <math> k_{Tv} </math> || Beiwert zur Berücksichtigung des Temperaturverlaufs in der Wand | ||
|- | |- | ||
| − | | <math> k_{Tv} \approx \cfrac{1}{2} \approx 0,5 </math> || für | + | | <math> k_{Tv} \approx \cfrac{1}{2} \approx 0,5 </math> || für h < 0,5m |
|- | |- | ||
| − | | <math> k_{Tv} \approx \cfrac{2}{3} \approx 0,7 </math> || für | + | | <math> k_{Tv} \approx \cfrac{2}{3} \approx 0,7 </math> || für h = 0,5 ... 3,0m |
|- | |- | ||
| − | |<math> k_{Tv} \approx 1,0 </math> || für | + | |<math> k_{Tv} \approx 1,0 </math> || für h > 0,5m |
|- | |- | ||
| <math> T_{c0} </math> || Frischbetontemperatur der Wand | | <math> T_{c0} </math> || Frischbetontemperatur der Wand | ||
|- | |- | ||
| − | | <math> \Delta T_{b,H} </math> || Temperaturdifferenz um die sich die Frischbetontemperatur bei der Hydratation erhöht | + | | <math> \Delta T_{b,H} </math> || Temperaturdifferenz, um die sich die Frischbetontemperatur bei der Hydratation erhöht |
|} | |} | ||
| Zeile 250: | Zeile 250: | ||
:::{| | :::{| | ||
| − | | <math> \alpha_b </math> || Beiwert zur Berücksichtigung des Verhältnisses zwischen Temperaturerhöhung im Bauteil und | + | | <math> \alpha_b </math> || Beiwert zur Berücksichtigung des Verhältnisses zwischen der tatsächlichen Temperaturerhöhung im Bauteil und der theoretischen Temperaturerhöhung der Wanddicke |
|- | |- | ||
| <math> z </math> || Zementgehalt | | <math> z </math> || Zementgehalt | ||
| Zeile 258: | Zeile 258: | ||
| <math> C_{c0} </math> || Wärmekapazität des Betons | | <math> C_{c0} </math> || Wärmekapazität des Betons | ||
|- | |- | ||
| − | | || < | + | | || C<sub>c0</sub> ≈ 2.500 kJ/(m<sup>3</sup> ∙ K) |
|} | |} | ||
| − | Anhand der folgenden Tabelle lässt sich der Beiwert α<sub>b</sub> zur Berücksichtigung des Verhältnisses zwischen Temperaturerhöhung im Bauteil und | + | Anhand der folgenden Tabelle lässt sich der Beiwert α<sub>b</sub> zur Berücksichtigung des Verhältnisses zwischen der tatsächlichen Temperaturerhöhung im Bauteil und der theoretischen Temperaturerhöhung der Wanddicke ablesen. |
{| class="wikitable" style="margin: auto;" | {| class="wikitable" style="margin: auto;" | ||
|+style="text-align: left;" | Verhältniswert α<sub>b</sub> | |+style="text-align: left;" | Verhältniswert α<sub>b</sub> | ||
| − | <ref name = " | + | <ref name = "Q1"></ref> |
|- | |- | ||
|rowspan="2"| | |rowspan="2"| | ||
| Zeile 299: | Zeile 299: | ||
|} | |} | ||
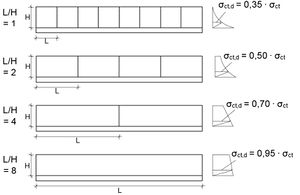
| − | [[Datei:Zwang - Bauteile mit wesentlichen Zwangsbeanspruchungen 3.jpeg|300px|thumb|right| | + | [[Datei:Zwang - Bauteile mit wesentlichen Zwangsbeanspruchungen 3.jpeg|300px|thumb|right|Spannungsverteilung in einer Wand<ref name = "Q4"> </ref>]] |
| − | Eine weitere Reduzierung der entstehenden Spannungen erfolgt durch die Relaxation (Verformung konstant, Abbau der Spannungen) und das Kriechen (Spannungen konstant, Abbau der Verformungen). Der Nachweis hierfür ist jedoch sehr aufwendig und wird an dieser Stelle nicht aufgeführt, was zu Ergebnissen auf der sicheren Seite liegend, führt. <ref name = " | + | Eine weitere Reduzierung der entstehenden Spannungen erfolgt durch die Relaxation (Verformung konstant, Abbau der Spannungen) und das Kriechen (Spannungen konstant, Abbau der Verformungen). Der Nachweis hierfür ist jedoch sehr aufwendig und wird an dieser Stelle nicht aufgeführt, was zu Ergebnissen auf der sicheren Seite liegend, führt. <ref name = "Q1"> </ref> <br/> |
| − | Die Größe der Zwangsbeanspruchungen ist unter anderem vom Verhältnis der Wandlänge L zur Wandhöhe H abhängig. Nach den Untersuchungsergebnissen von H. Falkner nehmen die Zwangsspannungen bei zunehmendem Verhältnis L/H zu und streben bei L/ | + | Die Größe der Zwangsbeanspruchungen ist unter anderem vom Verhältnis der Wandlänge L zur Wandhöhe H abhängig. Nach den Untersuchungsergebnissen von H. Falkner nehmen die Zwangsspannungen bei zunehmendem Verhältnis L/H zu und streben bei L/H ≈ 10 ihren Größtwert an.<ref name = "Q1"> </ref> <br/> |
| − | Der Maximalwert der in der Wand entstehenden Zwangsspannung stellt sich am Wandfuß ein. Da der Verbund mit der Sohlplatte jedoch bis in eine Wandhöhe von | + | Der Maximalwert der in der Wand entstehenden Zwangsspannung stellt sich am Wandfuß ein. Da der Verbund mit der Sohlplatte jedoch bis in eine Wandhöhe von 1/4 ∙ H bzw. ca. 80 cm über Oberkante Sohlplatte rissbreitenbegrenzend wirkt, wird die Bemessung mit dieser Spannung empfohlen (siehe dazu das nebenstehende Bild). Da sich die Sohlplatte beim Temperaturanstieg in der Wand kurz nach dem Betonieren erwärmt und somit die Verteilung der Zwangsspannungen im Bereich der Fuge allmählich erfolgt, darf die in der Spannungsverteilung entstehende spitze Ecke ausgerundet werden. Die empfohlene Anpassung des Spannungsverlaufes in der Wand an die Realität bzgl. der Spannungsordinate und der Ausrundung dieser werden mit dem Beiwert k<sub>ct,d</sub> wie folgt berücksichtigt.<ref name = "Q1"> </ref> |
:: <math> \sigma_{ct,d} = k_{ct,d} \cdot \sigma_{ct,cal} </math> | :: <math> \sigma_{ct,d} = k_{ct,d} \cdot \sigma_{ct,cal} </math> | ||
:::{| | :::{| | ||
| − | | <math> \sigma_{ct,d} </math> || Bemessungswert der Betonzugspannungen in ca. | + | | <math> \sigma_{ct,d} </math> || Bemessungswert der Betonzugspannungen in ca. 1/4 ∙ H |
|- | |- | ||
| <math> k_{ct,d} </math> || Beiwert zur Anpassung des Spannungsverlaufes in Abhängigkeit vom Verhältnis der Wandlänge L zur Wandhöhe H | | <math> k_{ct,d} </math> || Beiwert zur Anpassung des Spannungsverlaufes in Abhängigkeit vom Verhältnis der Wandlänge L zur Wandhöhe H | ||
|- | |- | ||
| − | | <math> \sigma_{ct, | + | | <math> \sigma_{ct,cal} </math> || Rechenwert der Betonzugspannung, die infolge Zwangsspannungen durch das Abfließen der Hydratationswärme entsteht |
|} | |} | ||
| − | In der nachfolgenden Tabelle werden die Beiwerte k<sub>ct,d</sub> in Abhängigkeit des Verhältnisses L/H | + | In der nachfolgenden Tabelle werden die Beiwerte k<sub>ct,d</sub> in Abhängigkeit des Verhältnisses L/H angegeben. |
{| class="wikitable" style="margin: auto;" | {| class="wikitable" style="margin: auto;" | ||
|+style="text-align: left;" | Beiwert k<sub>ct,d</sub> | |+style="text-align: left;" | Beiwert k<sub>ct,d</sub> | ||
| − | <ref name = " | + | <ref name = "Q1"></ref> |
|- | |- | ||
|rowspan="2"| | |rowspan="2"| | ||
| Zeile 363: | Zeile 363: | ||
== Quellen == | == Quellen == | ||
| − | :''Normen'' | + | :''Fachliteratur / Normen'' |
| − | <references | + | <references/> |
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| + | |||
Aktuelle Version vom 3. April 2019, 09:42 Uhr
Allgemeines
Die in diesem Abschnitt behandelten Berechnungsverfahren zur Ermittlung der Zwangsschnittgrößen in Sohlplatten und Wänden gelten als Empfehlung, die im „Lohmeyer Stahlbetonbau“ [1] gegeben wird und stellen eine Ergänzung zu der in der DIN EN 1992-1-1 [2] angegebenen Ermittlung der rissbreitenbegrenzenden Bewehrung dar.
verminderter Zwang in Sohlplatten
Kann eine Beanspruchung aus spätem Zwang, z.B. während der Bauphase oder des Nutzungszeitraumes, ausgeschlossen werden, darf der Nachweis für den frühen Zwang aus dem Abfließen der Hydratationswärme geführt werden. Zusätzlich dazu kann die Zwangsspannung vermindert werden, wenn in der Sohlplatte keine anderen Zwangsbeanspruchungen wirken und die Sohlplattenbewegungen nicht durch Festpunkte behindert werden. Die rechnerische Zugspannung in der Sohlplatte σct,d ist abhängig vom Reibungsbeiwert μd, der Spannung σ0 und der Länge L der verschiebbaren Sohlplatte.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,d} = \cfrac{\gamma_{ct} \cdot \mu_d \cdot \sigma_0 \cdot L}{2 \cdot a_{ct}} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,d} } Bemessungswert der wirksamen Betonzugspannung, die durch die Reibung auf dem Untergrund entsteht, wenn sich die Sohlplatte verkürzt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_{ct} } Sicherheitsbeiwert im Grenzzustand der Gebrauchstauglichkeit γct = 1,0 wenn die Zwangsspannung durch das Abfließen der Hydratationswärme hervorgerufen wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_d } Bemessungswert des Reibungsbeiwertes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cfrac{L}{2} } Reibungslänge der Sohlplatte halbe Sohlplattenlänge, da der Verformungsnullpunkt in Plattenmitte angenommen wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{ct} } Betonquerschnittsfläche, die auf Zug beansprucht ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{ct} = h \cdot b }
Reibungsbeiwerte für unterschiedliche Untergründe sind in der folgenden Tabelle aufgelistet. Ein Reibungsbeiwert darf nur bei Sohlplatten mit ebener Unterseite angesetzt werden, die sich auf dem Untergrund frei bewegen können und deren Verformungen nicht durch Fundamentvertiefungen, wie z.B. bei Aufzugschächten behindert werden. [1]
| 1 | 2 | 3 | |
| Unterkonstruktion a) | Trennlage | Reibungsbeiwert μ0 für die erste Verschiebung | |
|---|---|---|---|
| 1 | grobkörniger Baugrund ohne Sandbettung | keine | 1,4 … 2,1 e) |
| 2 | Kies-Sand-Bodenaustausch (nicht bindig) | bei Dicke der Bodenplatte h = 0,2m | > 1,4 |
| 3 | bei Dicke der Bodenplatte h = 0,8m | ≈ 0,9 | |
| 4 | sandiger Baugrund oder grobkörniger Baugrund mit Sandbettung unter der Sohlplatte | keine | 0,9 … 1,1 e) |
| 5 | Noppenbahn (d ≈ 0,6mm) | 0,8 … 1,0 d), e) | |
| 6 | 1 Lage PE-Folie b) | 0,5 … 0,7 d), e) | |
| 7 | Sandbett (Dicke 6 … 10cm, mittlere Korngröße 0,35mm) | keine (Direktauflagerung auf nicht feinkörnigem, bindigem Boden) | 0,7 |
| 8 | Perimeterdämmung auf Unterbeton bei beliebigem Baugrund | bei Dicke der Bodenplatte h ≤ 0,3m | ≈ 0,8 d) |
| 9 | bei Dicke der Bodenplatte h ≥ 0,8m | ≈ 0,5 d) | |
| 10 | Unterbeton abgezogen (makrorau) | 2 Lagen PE-Folie b) je 0,2mm: | |
| 11 | bei Dicke der Bodenplatte h = 0,3m | ≤ 2,0 | |
| 12 | bei Dicke der Bodenplatte h = 1,5m | ≤ 1,3 | |
| 13 | Bitumenschweißbahn c) | 0,35 … 0,7 d), e) | |
| 14 | Dickbitumen c) | 0,03 … 0,2 d), e) | |
| 15 | Trennschicht aus 2 Lagen dicker PE-Folie b) mit zwischenliegender Schicht aus Silikonfett als Schmiermittel | ≈ 0,8 | |
| 16 | Unterbeton mit Flügelglättung | 1 Lage PE-Folie b) | 0,8 … 1,4 d), e) |
| 17 | 2 Lagen PE- Folie b) | ≤ 0,8 | |
| 18 | mit PTFE b) beschichtete Folie | 0,2 … 0,5 e) | |
| 19 | Trennschicht aus 2 Lagen dicker PE-Folie b) mit zwischenliegender Schicht aus Silikonfett als Schmiermittel | ≈ 0,3 | |
| 20 | 1- bis 2-lagige Bitumenschweißbahn c), stumpf gestoßen: | ||
| 21 | bei Dicke der Bodenplatte h = 0,3m | ≈ 0,45 | |
| 22 | bei Dicke der Bodenplatte h > 1,0m | ≈ 0,2 | |
| 23 | Sicherheitsbeiwert für Reibung h) | γR = 1,35 f) | |
| 24 | γR =1,25 g) | ||
| 25 | Bemessungswert der Reibung | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_d = \gamma_R \cdot \mu_0 } | |
| a) Die Oberfläche der Unterkonstruktion muss den Anforderungen der Ebenheit nach DIN 18202 entsprechen. b) PE = Polyethylen, PTFE = Polytetrafluor- Ethylen c) Bituminöse Trennschichten sind nur bei ausreichender Schichtdicke und Temperaturen in der Trennschicht >10°C wirksam. d) Vorschlag der Autoren der Fachliteraturquellen e) Bewegt sich der Reibungsbeiwert in einer Spannbreite empfehlen die Autoren der Fachliteraturquellen die Annahme des höheren Wertes, wenn kein Einfluss auf die Ausführung besteht. f) nach "Lohmeyer Stahlbetonbau" [1] und "Weiße Wannen einfach und sicher - 9.Auflage" [3] g) nach "Weiße Wannen einfach und sicher - 11.Auflage"[4] h) Die Autoren der Fachliteraturen empfehlen mit den angegebenen Sicherheitsbeiwerten zu rechnen, da die Auswahl des Reibungsbeiwertes mit einiger Unsicherheit behaftet ist. | |||
verminderter Zwang in Wänden
Durch das nachträgliche Betonieren einer Wand auf eine Sohlplatte entstehen in der Wand Zwangsspannungen infolge der Verformungsbehinderung durch den Verbund beider Bauteile. Die ersten wesentlichen Zwangsbeanspruchungen treten in der Wand beim Abfließen der Hydratationswärme auf. [1]
Wenn der späte Zwang z.B. Temperaturänderungen im Tages- oder Jahreswechsel mit Sicherheit ausgeschlossen werden kann, darf die in der Wand entstehende Zwangsspannung wie folgt abgeschätzt werden.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,cal} = k \cdot \alpha_T \cdot E_{c,t} \cdot \Delta T_{b,W-F} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,cal} } Rechenwert der Betonzugspannung, die infolge Zwangsspannungen durch das Abfließen der Hydratationswärme entsteht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k } Beiwert für die Behinderung der Verformungsmöglichkeit eines Bauteils k = 1,0 für Wände, die auf ein anderes Bauteil, z.B. eine Sohlplatte betoniert werden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_T } Temperaturausdehnungskoeffizient des Betons αT = 10 ∙ 10-6 1/K Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_{c,t} } wirksamer Elastizitätsmodul des Betons zum Zeitpunkt tmaxT der Entstehung der Betonzugspannungen Ec,t = αE ∙ Ecm tmaxT = 1 + 0,8 ∙ h h in m Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta T_{b,W-F} } Temperaturdifferenz zwischen der mittleren Bauteiltemperatur der Wand und der Sohlplatte
Anhand der folgenden Tabelle lässt sich der Verhältniswert αE der Elastizitätsmoduln in Abhängigkeit des Bauteilalters tmaxT bei Entstehung der Betonzugspannungen ablesen.
| 1 | 2 | |
| Betonalter | Verhältniswert αE = Ec,t/Ecm | |
|---|---|---|
| 1 | 12 Stunden | 0,25 |
| 2 | 16 Stunden | 0,45 |
| 3 | 24 Stunden | 0,65 |
| 4 | 48 Stunden | 0,85 |
| 5 | 14 Tage | 1 |
Die Temperaturdifferenz zwischen der mittleren Bauteiltemperatur der Wand und der Bauteiltemperatur der Sohlplatte bzw. des Fundamentes lässt sich wie folgt ermitteln.[1]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta T_{b,W-F} = T_{b,m} - T_F }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{b,m} } mittlere Bauteiltemperatur der Wand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_F } Bauteiltemperatur des Fundamentes bzw. der Sohlplatte
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{b,m} = k_{Tv} \cdot T_{c0} + \Delta T_{b,H} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{Tv} } Beiwert zur Berücksichtigung des Temperaturverlaufs in der Wand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{Tv} \approx \cfrac{1}{2} \approx 0,5 } für h < 0,5m Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{Tv} \approx \cfrac{2}{3} \approx 0,7 } für h = 0,5 ... 3,0m Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_{Tv} \approx 1,0 } für h > 0,5m Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{c0} } Frischbetontemperatur der Wand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta T_{b,H} } Temperaturdifferenz, um die sich die Frischbetontemperatur bei der Hydratation erhöht
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta T_{b,H} = \alpha_b \cdot \cfrac{z \cdot Q_H}{C_{c0}} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_b } Beiwert zur Berücksichtigung des Verhältnisses zwischen der tatsächlichen Temperaturerhöhung im Bauteil und der theoretischen Temperaturerhöhung der Wanddicke Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z } Zementgehalt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q_H } Hydratationswärme des Zementes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_{c0} } Wärmekapazität des Betons Cc0 ≈ 2.500 kJ/(m3 ∙ K)
Anhand der folgenden Tabelle lässt sich der Beiwert αb zur Berücksichtigung des Verhältnisses zwischen der tatsächlichen Temperaturerhöhung im Bauteil und der theoretischen Temperaturerhöhung der Wanddicke ablesen.
| 1 | 2 | |
| Bauteildicke h [m] | Verhältniswert αb = ΔTb,H/ΔTth | |
|---|---|---|
| 1 | 0,25 | 0,65 |
| 2 | 0,40 | 0,75 |
| 3 | 0,60 | 0,80 |
| 4 | 0,80 | 0,85 |
| 5 | 1,00 | 0,90 |
| 6 | 2,00 | 1,00 |
Eine weitere Reduzierung der entstehenden Spannungen erfolgt durch die Relaxation (Verformung konstant, Abbau der Spannungen) und das Kriechen (Spannungen konstant, Abbau der Verformungen). Der Nachweis hierfür ist jedoch sehr aufwendig und wird an dieser Stelle nicht aufgeführt, was zu Ergebnissen auf der sicheren Seite liegend, führt. [1]
Die Größe der Zwangsbeanspruchungen ist unter anderem vom Verhältnis der Wandlänge L zur Wandhöhe H abhängig. Nach den Untersuchungsergebnissen von H. Falkner nehmen die Zwangsspannungen bei zunehmendem Verhältnis L/H zu und streben bei L/H ≈ 10 ihren Größtwert an.[1]
Der Maximalwert der in der Wand entstehenden Zwangsspannung stellt sich am Wandfuß ein. Da der Verbund mit der Sohlplatte jedoch bis in eine Wandhöhe von 1/4 ∙ H bzw. ca. 80 cm über Oberkante Sohlplatte rissbreitenbegrenzend wirkt, wird die Bemessung mit dieser Spannung empfohlen (siehe dazu das nebenstehende Bild). Da sich die Sohlplatte beim Temperaturanstieg in der Wand kurz nach dem Betonieren erwärmt und somit die Verteilung der Zwangsspannungen im Bereich der Fuge allmählich erfolgt, darf die in der Spannungsverteilung entstehende spitze Ecke ausgerundet werden. Die empfohlene Anpassung des Spannungsverlaufes in der Wand an die Realität bzgl. der Spannungsordinate und der Ausrundung dieser werden mit dem Beiwert kct,d wie folgt berücksichtigt.[1]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,d} = k_{ct,d} \cdot \sigma_{ct,cal} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,d} } Bemessungswert der Betonzugspannungen in ca. 1/4 ∙ H Beiwert zur Anpassung des Spannungsverlaufes in Abhängigkeit vom Verhältnis der Wandlänge L zur Wandhöhe H Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,cal} } Rechenwert der Betonzugspannung, die infolge Zwangsspannungen durch das Abfließen der Hydratationswärme entsteht
In der nachfolgenden Tabelle werden die Beiwerte kct,d in Abhängigkeit des Verhältnisses L/H angegeben.
| 1 | 2 | |
| Verhältnis L/H a) | Beiwert kct,d | |
|---|---|---|
| 1 | ≤ 1 | ≈ 0,35 |
| 2 | ≤ 2 | ≈ 0,50 |
| 3 | ≤ 3 | ≈ 0,60 |
| 4 | ≤ 4 | ≈ 0,70 |
| 5 | ≤ 6 | ≈ 0,85 |
| 6 | ≤ 8 | ≈ 0,95 |
| 7 | ≤ 10 | ≈ 1,00 |
| 8 | > 10 | = 1,00 |
| a) Verhältnis der Wandlänge L (Abstand zwischen zwei Fugen) zur Wandhöhe H | ||
Quellen
- Fachliteratur / Normen
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 Baar, S.; Ebeling, K.: Lohmeyer Stahlbetonbau. Bemessung-Konstruktion-Ausführung. 10.Auflage. Wiesbaden 2017
- ↑ DIN EN 1992-1-1 Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau mit Nationalem Anhang. Beuth Verlag GmbH 2016
- ↑ 3,0 3,1 Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 9. überarbeitete und erweiterte Auflage. Düsseldorf 2009
- ↑ 4,0 4,1 4,2 Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 11. überarbeitete Auflage. Düsseldorf 2018
Seiteninfo
|

