Durchstanzen: Unterschied zwischen den Versionen

Aus Baustatik-Wiki
Zur Navigation springen Zur Suche springen
 
(252 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
===Allgemeines zum Durchstanzen===
 
  
 +
<br />
  
−
Wird eine '''konzentrierte Last''' auf eine verhältnismäßig '''kleine Einleitungsfläche''' eines
+
==Allgemeines zum Durchstanzen==
−
Plattentragwerks (z.B. Deckenplatte oder Fundament) aufgebracht, so kommt
 
−
es zu einem '''örtlichen Querkraftversagen''' <ref>K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref>. Dies äußert sich bei relativ geringen
 
−
Lasten durch auftretende Biegerisse in radialer Richtung. Wird die Last erhöht, so kommt es als Folge dessen zum Reißen des Betons in tangentialer Richtung (Querkraftrisse). Durch die Vereinigung zu Durchstanzrissen verursachen diese einen '''Bruch''' <ref>Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>.
 
−
Trennt sich der betroffenen Plattenbereich heraus, so entsteht der typische kegel- oder pyramidenförmige Körper. Diese Art des Versagens geschieht ohne eine ausgeprägte
 
−
Vorankündigung. Es kommt zu einem fortschreitenden Kollaps der vollständigen Konstruktion <ref>Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken
 
−
und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012</ref>. Folglich ist diese Art von Nachweis das '''maßgebende''' '''Kriterium bei der Bemessung einer Deckenplatte'''. Da das Durchstanzversagen ein Sonderfall der Querkraftbeanspruchung darstellt, besteht ein Zusammenhang zwischen
 
−
beiden Bemessungsansätzen <ref>Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012</ref>. Obwohl die Durchstanztragfähigkeit und
 
−
das Biegetragverhalten sich gegenseitig beeinflussen (siehe Bild 1), sind ihre Berechnung separat durchzuführen. <ref>Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.
 
−
Skript</ref>.
 
−
Die '''Durchstanztragfähigkeit''' wird durch Bauteileigenschaften wie
 
−
*der '''Betonfestigkeit''',
 
−
*den '''Querschnittabmessungen''',
 
−
*der '''Bewehrungsmenge in der Zugzone''',
 
−
*eine durch Vorspannung entstehende '''Normaldruckkraft''' und
 
−
*die vorgesehene '''Durchstanzbewehrung''' maßgebend beeinflusst <ref>Prof Dr.-Ing. Guido Bolle. Skript: Modul - Stahlbetonbau 2</ref>.
 
  
−
Bei der Nachweisführung müssen folgende '''Versagen verursachende Komponenten'''
+
Wird eine ''konzentrierte Last'' auf eine verhältnismäßig ''kleine [[Durchstanzen - Lasteinleitungsfläche und kritischer Rundschnitt|Einleitungsfläche]]'' eines Plattentragwerks (z. B. Deckenplatte oder Fundament) aufgebracht, so kommt
−
einbezogen werden <ref>Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>:
+
es zu einem ''örtlichen Querkraftversagen''  
−
*eine '''Überschreitung der Betonzugfestigkeit''',
+
<ref name = "Q1">K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref>.<br />
−
*ein '''Versagen der Betondruckzone''',
+
Dies äußert sich bei relativ geringen Lasten zunächst durch auftretende Biegerisse in radialer Richtung. Wird die Last erhöht, so kommt es als Folge dessen zum Reißen des Betons in tangentialer Richtung (Querkraftrisse). <br />
−
*ein '''örtliches Verbundversagen''' der Biegezugbewehrung
+
Durch die Vereinigung beider Rissformen zu Durchstanzrissen wird der ''Bruch'' eingeleitet.
−
*und eine '''unzureichende Verankerung''' der Durchstanzbewehrung
+
<ref name = "Q2">Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>.
−
Der zu führende Nachweis besagt, dass die auf den kritischen Rundschnitt <math> d \cdot u </math> bezogene einwirkende Querkraft <math>\nu_ {Ed}</math> geringer ausfällt, als der Bemessungswiderstand <math>\nu_{Rd}</math>.
+
<br />
−
Der Nachweis lautet wie folgt:
+
Dabei wird der betroffene Plattenbereich aus der übrigen Platte herausgetrennt und es entsteht der typische kegel- oder pyramidenförmige Körper. Diese Art des Versagens geschieht ohne eine ausgeprägte Vorankündigung. Es kommt zu einem fortschreitenden Kollaps der vollständigen Konstruktion
−
<math>\nu_ {Ed}=\beta \cdot \frac{V_{Ed}}{u_i \cdot d} \leq \nu_ {Rd}</math>
+
<ref name = "Q3">Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012</ref>.
−
Es findet hierbei eine Unterscheidung in Bauteilen mit und ohne Durchstanzbewehrung
+
<br />  
−
statt.
+
Folglich ist der Nachweis einer ausreichenden Durchstanztragfähigkeit eines der ''maßgebenden Kriterien '' bei der Bemessung einer punktgestützten bzw. durch Einzellasten beanspruchten Deckenplatte. Da das Durchstanzen ein Sonderfall der Querkraftbeanspruchung darstellt, besteht ein Zusammenhang zwischen beiden Bemessungsansätzen
 +
<ref name = "Q4">Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012</ref>.  
  
−
===Bauteile ohne Durchstanzbewehrung===
+
Obwohl das Durchstanz- und das Biegetragverhalten sich gegenseitig beeinflussen (siehe Bild), sind die Nachweise jeweils separat zu führen. <ref name = "Q5">Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript</ref>.
 +
<br />
 +
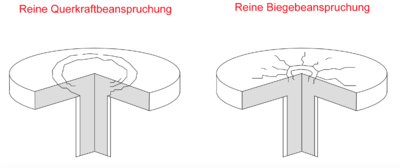
[[Datei:Durchstanzen_1.png|400px|thumb|right| Rissbilder bei reiner Querkraft- und reiner Biegebeanspruchung ]]
  
−
Bei Plattentragwerken ohne Durchstanzbewehrung (siehe Bild 2) muss der folgende Nachweis klären, ob die Tragfähigkeit des Betons im kritischen Rundschnitt ausreichend ist und die auftretende Querkraft den Bauteilwiderstand somit nicht überschreitet <ref>Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>.
 
−
Im Allgemeinen gilt:
 
−
<math> \nu_ {Ed}\leq\nu_ {Rd}</math>
 
−
Somit muss bei Bauteilen ohne Durchstanzbewehrung die Querkrafttragfähigkeit des Betons im kritischen Rundschnitt größer sein, als die vorherrschende Einwirkung:
 
−
<math> \nu_ {Ed}\leq\nu_ {Rd,c}</math>
 
  
−
Ist der Bemessungswiderstand <math>\nu_ {Ed}</math> größer als der Bemessungswert der Querkraft <math>\nu_ {Rd}</math> , so ist eine Durchstanzbewehrung vorzusehen, welche beispielsweise durch Bügel gebildet werden kann. Ist diese Maßnahme nicht ausreichend, können tragfähigkeitserhöhende Einbauteile vorgesehen werden<ref>Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012</ref>.
+
Die ''Durchstanztragfähigkeit'' wird durch Bauteileigenschaften wie
 +
<br />
 +
*die ''Betonfestigkeit'',
 +
*die ''Querschnittabmessungen'',
 +
*die ''Bewehrungsmenge in der Zugzone'',
 +
*eine durch Vorspannung entstehende ''Normaldruckkraft'' und
 +
*die vorgesehene ''Durchstanzbewehrung'' maßgebend beeinflusst <ref name = "Q6">Prof Dr.-Ing. Guido Bolle. Skript: Modul - Stahlbetonbau 2</ref>.
 +
<br />
 +
Bei der Nachweisführung müssen folgende ''Versagen verursachende Komponenten'' einbezogen werden <ref name="Q2" />:
 +
<br />
 +
*eine ''Überschreitung der Betonzugfestigkeit'',
 +
*ein ''Versagen der Betondruckzone'',
 +
*ein ''örtliches Verbundversagen'' der Biegezugbewehrung
 +
*und eine ''unzureichende Verankerung'' der Durchstanzbewehrung
 +
<br />
 +
<br />Der allgemein zu führende Nachweis besagt, dass die auf einen [[Durchstanzen - Lasteinleitungsfläche und kritischer Rundschnitt|Rundschnitt]] <math> d \cdot u </math> (besser: die Rundschnittfläche) bezogene einwirkende Querkraft <math>\nu_ {Ed}~</math> geringer ausfällt, als der Bemessungswiderstand <math>\nu_{Rd}~</math>.<br />
 +
<br />
  
−
===Bauteile mit Durchstanzbewehrung===
+
Der ''allgemeine Nachweis'' lautet wie folgt:
 +
<br />
 +
:<math> \nu_ {Ed}\leq\nu_ {Rd}</math>
 +
<br />
  
−
Wird Durchstanzbewehrung benötigt, so muss auf mehreren Rundschnitten ui weitere Querkraftnachweise geführt werden <ref>Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>. Des Weiteren kann zur Steigerung der Tragfähigkeit zusätzlich zur Durchstanzbewehrung eine Querkraftbewehrung in Form von aufgebogenen Stäben, Bügeln, S-Haken oder Dübelleisten in Betracht gezogen werden. Werden solche verwendet, ist eine zweite Reihe an Schubbewehrung anzuordnen, auch wenn diese rechnerisch
+
:wobei
−
nicht erforderlich ist<ref>Dipl.-Ing. Klaus Beer. Bewehren nach DIN EN 1992-1-1(EC2). Vieweg+Teubner, S. 196-207, 3. Aufl. edition, 2012</ref>. Bei der Ausführung von Durchstanzbewehrung müssen mehrere Versagensmechanismen (siehe Bild 3) betrachtet werden <ref>Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>:
+
<br />
  
−
'''Betonversagen:''' die maximale Schubspannung <math>\nu_ {Rd,Ed}</math> nach Gleichung (1) darf nicht größer ausfallen, als der Bemessungswert des maximalen Durchstanzwiderstands <math>\nu_ {Rd,max}</math>.
+
::<math>\nu_ {Ed}~</math> - Bemessungswert der einwirkenden Querkraft je Flächeneinheit im betrachteten Rundschnitt
−
<math> \nu_ {Ed}\leq\nu_ {Rd,max}</math>
+
::<math>\nu_ {Rd}~</math> - Bemessungswert des Durchstanzwiderstandes je Flächeneinheit im betrachteten Rundschnitt
 +
<br />
 +
Bei der Ermittlung des Durchstanzwiderstandes <math>\nu_{Rd}~</math> unterscheidet man
 +
* Bauteile ohne Durchstanzbewehrung
 +
* Bauteile mit Durchstanzbewehrung
 +
<br />
  
−
'''Stahlversagen:''' die Tragfähigkeit des Querschnitts mit Durchstanzbewehrung muss in jedem Rundschnitt gewährleistet sein.
+
==Bemessungswert der einwirkenden Querkraft==
−
<math>\nu_ {Ed}\leq\nu_ {Rd,cs}</math>
+
<br />
−
Die Querkrafttragfähigkeit muss in der Umgebung '''außerhalb des durchstanzbewehrtem Bereichs ohne Querkraftbewehrung''' gegeben sein.
+
Genauere Informationen zur Ermittlung des Bemessungswertes der einwirkenden Querkraft finden Sie hier: [[Durchstanzen - Bemessungswert der einwirkenden Querkraft]]
−
<math>\nu_ {Ed}\leq\nu_ {Rd,c,out}</math>
 
  
−
===Lasteinleitungsfläche und kritischer Rundschnitt===
+
==Bauteile ohne Durchstanzbewehrung==
 +
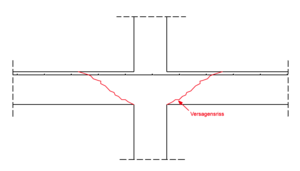
[[Datei:Durchstanzen_2.png|300px|thumb|right|Versagensmechanismus bei einem Bauteil ohne Durchstanzbewehrung ]]
 +
Bei Plattentragwerken ohne Durchstanzbewehrung (siehe Bild) muss nachgewiesen werden, dass der Bemessungswert der einwirkenden Querkraft im kritischen Rundschnitt den Bemessungswert der Durchstanztragfähigkeit ohne Durchstanzbewehrung nicht überschreitet.
 +
<br />
 +
Die Bedingung lautet:
 +
<br />
 +
:<math> \nu_ {Ed}\leq\nu_ {Rd,c}</math>
 +
<br />
  
−
Die Bemessung der Lasteinleitungsfläche Aload mit dem kritischen Rundschnitt u1 gilt für folgende Geometrien:
+
:wobei
−
*Rundstützen mit dem Umfang <math>u_0 \leq 12d</math>
+
<br />
−
*Rechteckstützen mit <math>u_0 \leq 12d</math> und dem Verhältnis von Länge zu Breite<math> \leq 2</math>
 
−
*andere Formen, die sinnvoll wie oben genannt begrenzt werden können
 
−
 
 
−
Dabei wird die benötigte statische Nutzhöhe d wie folgt ermittelt:
 
−
 
 
−
<math> \frac{(d_x+d_y)}{2}</math>
 
−
 
 
−
Die Lasteinleitungsfläche darf sich nicht in der Nähe von anderen konzentrierten Lasten sowie anderen wirkenden Querkräften befinden, was eine Überschneidung der kritischen Rundschnitte zur Folge hätte [1]. Ist dies dennoch der Fall, so ist im Durchstanznachweis der gesamte Rundschnittumfang mit der kleinsten Umhüllenden unter Berücksichtigung der Umfangsbegrenzung der Lasteinleitungsfläche von 12d in Ansatz zu bringen (Nationaler Anhang (NA)) [2]. Einwirkung und Widerstand werden auf den kritischen Rundschnitt bezogen, dieser wird bei Rund- und Rechteckstützen im Abstand 2d von der Lasteinleitungsfläche gebildet (siehe Bild 4) [5]. Die kritische Fläche Acont stellt die Fläche innerhalb des kritischen Rundschnitts u1 dar (siehe Bild 5 und 6) .
 
−
 
 
−
Bei der Ermittlung des kritischen Rundschnitts sind einspringende Ecken zu überlesen, da der kleinste aller Rundschnitte maßgebend ist [5]. Die Berücksichtigung eines Rundschnitts kleiner als 2d ist dann notwendig, wenn ein großer Gegendruck beispielsweise durch Sohldruck bei Fundamenten, einer Auflagerreaktion oder einer Last innerhalb des kritischen Rundschnitts (2d) vorherrscht.
 
−
Trifft dieser Fall zu, so ist der Abstand acrit iterativ zu ermitteln (NA) [2]. Sind die oben genannten Bedingungen in Bezug auf die rechteckige Lasteinleitungsfläche nicht erfüllt, so darf nur ein reduzierter kritischer Rundschnitt in Ansatz gebracht werden [4].
 
−
 
 
−
===Ausgedehnte Einleitungsflächen===
 
−
Ist das Seitenverhältnis <math>a/b > 2 </math> oder der Umfang der Lasteinleitungsfläche <math>A_{load} > 12d</math>, so müssen gesonderte Nachweise geführt werden, welche nur auf Teilrundschnitte mit <math>u_0 \ge 12d</math> zu beziehen sind (siehe Bild 7). Der Querkraftwiderstand ist für alle weiteren, über den Umfang hinaus ragenden Bereiche zu ermitteln. Die Summe aus der Durchstanztragfähigkeit sowie der Querkrafttragfähigkeit bildet den Gesamtwiderstand [5].
 
−
 
 
−
===Randnähe===
 
−
Liegt die Lasteinleitungsfläche nahe eines freien Randes, so ist der minimale kritische Rundschnitt möglicherweise nicht mehr geschlossen und endet in diesem Fall stets orthogonal zu diesem [5]. Im zutreffenden Fall ist der Rundschnitt wie in Bild 8 aufgezeigt anzunehmen. Dieser Rundschnitt wird jedoch nur maßgebend, wenn der Umfang kleiner ist als der des "Regelrundschnitts" bei geschlossener Schnittführung [8]. Beträgt der Abstand zum freien Rand < d, so ist in der Regel eine besondere Randbewehrung einzulegen [1].
 
−
 
 
−
===Öffnungen===
 
−
Liegt der Rand der Lasteinleitungsfläche im Abstand von weniger als 6d von einer Öffnung entfernt, so muss die der Öffnung zugewandte Seite des Rundschnitts als unwirksam betrachtet werden. Diese ist somit bei der Berechnung abzuziehen [9]. Der Umfang lässt sich somit wie in Bild 9 dargestellt bilden.
 
−
 
 
−
==Bemessungswert der Einwirkung==
 
−
Die als Spannung angegebene Bemessungsquerkraft bezieht sich auf die Querschnittsfläche
 
−
des kritischen Rundschnitts [5].
 
−
Die Gleichung dafür lautet:
 
−
<math>\nu_ {Ed}=\beta \cdot \frac{V_{Ed}}{u_i \cdot d} </math>
 
−
 
 
−
===Korrekturfaktor β ===
 
−
- nach EC 2-1-1, 6.4.3.(6)<ref>Prof. Dr.-Ing. Rudolf Baugart -Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences 2012</ref><ref>K. Zilch F. Fingerloos, J. Hegger- Eurocode 2 für Deutschland. Ernst + Sohn,
 
−
Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref><ref>Prof. Dr-Ing. Jens Minnert- Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012.</ref>
 
−
 
 
−
Infolge von Biegung ist die aufgebrachte Querkraft nicht mehr gleichmäßig über den Umfang verteilt, die Belastung einer Seite ist folglich erhöht. Der Lasterhöhungsfaktor β berücksichtigt diesen Umstand.
 
−
Zur Ermittlung des Faktors β stehen drei Verfahren zur Verfügung. Diese werden folgend erläutert:
 
−
 
 
−
===Konstanter Faktor für ausgesteifte Systeme mit nahezu gleichen Stützweiten===
 
−
 
 
−
Es werden horizontal unverschiebliche, ausgesteifte Systeme mit Stützweitenunterschieden
 
−
von maximal 25 % und eine Belastung durch Gleichlast angenommen. Die Stützweitenverhältnisse betragen somit <math>0,8\leq l_1/l_2\leq 1,25</math>.
 
−
 
 
−
Für diesen Fall können somit folgende konstante Näherungswerte angenommen
 
−
werden:
 
−
 
 
−
*1,10 Innenstützen
 
−
*1,40 Randstützen
 
−
*1,35 Wandenden (NA)
 
−
*1,50 Eckstützen
 
−
*1,20 Wandecken (NA)
 
−
*Bei Fundamenten wird ein <math> \beta \leq 1,10</math> angenommen.
 
−
 
 
−
===Ermittlung über Sektormodell===
 
−
Im ersten Schritt sind die Querkraftnulllinien anzusätzen. Diese werden abgeschätzt
 
−
oder errechnet (linear-elastisch). Anschließend findet eine Unterteilung
 
−
der Lasteinzugsfläche <math>A_{LE}</math> in i-Lasteinleitungssektoren  <math>A_i</math>  (siehe Bild 11) statt.
 
−
Hierbei sollten mindestens 3-4 Sektoren pro Quadrant betrachtet werden [1].
 
−
Der Lasterhöhungsfaktor ergibt sich somit wie folgt [2]:
 
−
<math> \nu_{Ed}=e_d \cdot A_{LE}</math>
 
−
 
 
−
<math> \nu_{Ed,m}=\nu_Ed \cdot u_{crit}</math>
 
−
 
 
−
<math> \nu_{Ed,i}=e_d \cdot \frac{A_i}{u_i}</math>
 
−
 
 
−
<math> \beta=max\{ \nu_{Ed,i}/\nu_{Ed,m}\}</math>
 
−
 
 
−
===Genaueres Verfahren===
 
−
 
 
−
nach EC 2-1-1, 6.4.3 (1;2)
 
−
 
 
−
Sind die oben genannten Voraussetzungen nicht erfüllt oder ist die bezogene Ausmitte <math>e/c</math> bei Randstützen größer als 1,2 (wobei c die Stützenabmessung in Richtung der Ausmitte darstellt), ist der Lasterhöhungsfaktor mit genaueren Verfahren
 
−
zu ermitteln. Hierbei wird die Annahme einer vollplastischen Schubspannungsverteilung am kritischen Rundschnitt getroffen.
 
−
Die Gleichung lautet somit wie folgt:
 
−
<math>\beta=1+k\cdot\frac{M_{Ed}}{V_{Ed}}\cdot\frac{u_1}{W_1}\le 1,10</math>
 
−
mit
 
−
<math> W_1=\int_0^{u_i} |e| dl</math>
 
−
und somit bei einer geschlossenen Rechteckstütze mit c1 parallel und c2 senkrecht
 
−
zur Lastausmitte:
 
−
<math>W_1=\frac{c_1^2}{2}+c_1c_2+4c_2d+16d^2+2\pi dc_1</math>
 
−
und dem Beiwert k
 
−
*Tabelle
 
−
Bei Decken-Stützenknoten mit zweiachsiger Ausmitte gilt (NA) [2]:
 
−
<math>W_1=1+\sqrt{(k_y\cdot\frac{M_{Ed,y}}{V_{Ed}}\cdot\frac{u_1}{W_{1,y}})^2+(k_z\cdot\frac{M_{Ed,z}}{V_{Ed}}\cdot\frac{u_1}{W_{1,z}})^2}\ge 1,10</math>
 
−
 
 
−
==Punktförmig gestützt Platten und Fundamente ohne Durchstanzbewehrung==
 
−
 
 
−
Bei Platten ohne Durchstanzbewehrung lautet der erforderliche Nachweis im kritischen
 
−
Rundschnitt wie folgt:
 
−
<math>\nu_{Ed}\le\nu_{Rd,c}=C_{Rd,c}\cdot k\cdot (100\cdot\rho_l\cdot f_{ck})^{^1/3}+k_1 \cdot \sigma_{cp}\ge\nu_{min}+k_1\cdot\sigma_{cp}</math>
 
−
Die '''Einflussfaktoren''' sind folglich die Betonfestigkeit, der Längsbewehrungsgrad, die Plattendicke sowie die Betonnormalspannung (z.B. infolge einer Vorspannung).
 
−
Für Flachdecken gilt im Allgemeinen:
 
−
<math>C_{Rd,c}=0,18/\gamma_c</math>
 
−
mit <math>\gamma_c=1,5</math>
 
−
Dieser empirische Vorwert beträgt für ständige und vorübergehende Bemessungssituationen CRd,c= 0,12.
 
−
 
 
−
Für Innenstützen bei Flachdecken mit dem Verhältnis <math>u0/d < 4</math> (mächtige Platte auf schlanker Stütze, siehe Bild 13) gilt (NA) [5]:
 
−
<math>C_{Rd,c}=0,18/\gamma_c\cdot (0,1\cdot u_0/d+0,6)</math>
 
−
 
 
−
Bei Rundstützen mit einem<math> u_0\ge 12d</math> ist das <math>C_{Rd,c}</math> wie folgt zu ermitteln, da man von einer querkraftbeanspruchten Flachdecke ausgeht [1]:
 
−
<math>C_{Rd,c}=\frac{12d}{u_0}\cdot\frac{0,18}{\gamma_c}\ge\frac{0,15}{\gamma_c}</math>
 
−
 
 
−
Weitere benötigte Parameter des Nachweises ergeben sich wie folgt:
 
−
*'''Maßstabsfaktor''' zur Berücksichtigung der Bauteilhöhe mit d in mm:
 
−
<math>k=1+\sqrt{\frac{200}{d}}\le 2,0</math>
 
−
*'''Bewahrungsgrad''', bezogen auf die mitwirkende Plattenbreite:
 
−
<math>\rho_l=\sqrt{\rho_{lx}\cdot\rho_{ly}}\le 0,02</math> und <math>\le 0,50\cdot\frac{f_{cd}}{f_{yd}}</math> (NA)
 
−
*'''Betonnormalspannung''' in N/mm2 (Druck positiv!):
 
−
<math>\sigma_{cp}=\frac{\sigma_{cx}+\sigma_{cy}}{2}</math>
 
−
*'''Mindesttragfähigkeit''': maßgebend, wenn <math>\nu_{min}\ge\nu_{Rd,c}</math>
 
−
<math>\nu_{min}=0,035\cdot k^{3/2}\cdot f_{ck}^{1/2}</math>
 
−
*<math>\nu_{min}=(0,0525/\gamma_c)\cdot k^{3/2}\cdot f_{ck}^{1/2}</math> für <math>d\le 600mm</math> (NA)
 
−
*<math>\nu_{min}=(0,0375/\gamma_c)\cdot k^{3/2}\cdot f_{ck}^{1/2}</math> für <math>d> 800mm</math> (NA)
 
−
 
 
−
Für <math>600 mm < d\le 800</math>mm darf interpoliert werden.
 
−
<math> k_1=0,10</math>
 
−
 
 
−
===Besonderheiten von Fundamenten===
 
−
Bei Bodenplatten und Stützenfundamenten darf in der Fläche <math>A_{crit}</math> die Einwirkung vollständig um den günstig wirkenden Sohldruck abgemindert werden. Durch die Bodenpressung und eine geringere Schubschlankheit fällt der Durchstanzkegel deutlich steiler aus als bei schlanken Deckenplatten. Aufgrund dieser Parameter ist die Lage des maßgeblichen Rundschnitts im Voraus nicht bekannt [10].
 
−
Die reduzierte Querkraftbeanspruchung ermittelt sich wie folgt:
 
−
<math>V_{Ed, red}=V_{Ed}-\delta V_{Ed}</math>
 
−
Dabei stellt <math>V_{Ed}</math> den resultierenden Sohldruck der kritischen Fläche ohne das Fundamenteigengewicht dar.
 
−
 
 
−
Der im Vornherein unbekannte Abstand <math>a_{crit}</math> lässt sich wie folgt ermitteln (NA):
 
  
 +
::<math>\nu_ {Ed}~</math> - Bemessungswert der einwirkenden Querkraft je Flächeneinheit im kritischen Rundschnitt
 +
::<math>\nu_ {Rd,c}~</math> - Bemessungswert des Durchstanzwiderstandes je Flächeneinheit einer Platte ohne Durchstanzbewehrung
 +
<br />
  
 +
Ist der Bemessungswiderstand <math>\nu_ {Ed}~</math> größer als der Bemessungswert der Querkraft <math>\nu_ {Rd,c}~</math> , so ist eine Durchstanzbewehrung vorzusehen, welche beispielsweise durch Bügel gebildet werden kann. Alternativ kann auch durch das Vergrößern der Längsbewehrung die Durchstanztragfähigkeit gesteigert werden.<br />
 +
<br />
 +
Genauere Informationen zum Nachweis für Bauteile ohne Durchstanzbewehrung : [[Durchstanzen - Punktförmig gestützte Platten und Fundamente ohne Durchstanzbewehrung|Punktförmig gestützte Platten und Fundamente ohne Durchstanzbewehrung]]
  
 +
==Bauteile mit Durchstanzbewehrung==
  
 +
Wird Durchstanzbewehrung benötigt, so muss auf mehreren Rundschnitten u<sub>i</sub> weitere Querkraftnachweise geführt werden<ref name="Q2" />.
 +
<br />
 +
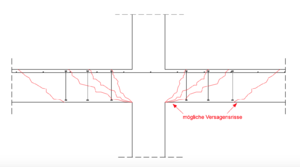
[[Datei:Durchstanzen_3.png|300px|thumb|right|Versagensmechanismus bei Bauteilen mit Durchstanzbewehrung ]]
 +
<br />
 +
Als Durchstanzbewehrung können folgende Bewehrungselemente zum Einsatz kommen:
 +
* Bügel
 +
* aufgebogene Stäbe
 +
* S-Haken
 +
* Dübelleisten
 +
* spezielle Gitterträger
 +
Je nach verwendeter Durchstanzbewehrung sind beim Verlegen der Bewehrung weitere Regel zu beachten.
 +
<br />
 +
Beim Nachweis von Bauteilen mit Durchstanzbewehrung sind folgende Einzelnachweise zu führen (siehe Bild)  <ref name="Q2" />:
 +
<br />
 +
* ''Betonversagen:'' die maximale Schubspannung <math>\nu_ {Rd,Ed}</math> darf nicht größer ausfallen, als der Bemessungswert des maximalen Durchstanzwiderstands <math>\nu_ {Rd,max}</math>.
 +
<br />
 +
::<math> \nu_ {Ed}\leq\nu_ {Rd,max}</math>
 +
<br />
 +
* ''Stahlversagen:'' die Tragfähigkeit des Querschnitts mit Durchstanzbewehrung muss in jedem Rundschnitt gewährleistet sein.
 +
<br />
 +
::<math>\nu_ {Ed}\leq\nu_ {Rd,cs}</math>
 +
<br />
 +
* ''Querkrafttragfähigkeit ohne Durchstanzbewehrung:'' außerhalb des durchstanzbewehrtem Bereichs muss die Querkrafttragfähigkeit ohne Durchstanzbewehrung nachgewiesen werden.
 +
<br />
 +
::<math>\nu_ {Ed}\leq\nu_ {Rd,c,out}</math>
 +
<br />
 +
Genauere Informationen zu dem Nachweis für Bauteile mit Durchstanzbewehrung: [[Durchstanzen - Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung|Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung]]
  
 +
==Beispiel: Berechnung einer Flachdecke mit einer Rundstütze==
 +
Ein Berechnungsbeispiel findet man auf der Seite: [[Durchstanzen - Flachdecke mit einer Rundstütze (Bsp.)|Flachdecke mit einer Rundstütze (Bsp.)]]
  
 
[[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]]
 
[[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]]
−
*gedrungene Fundamente <math>\lambda \le 2,0 </math>: interactive Ermittlung des kritischen Rundschnitts
 
−
*schlanke Fundamente <math>\lambda >2,0</math>: konstanter Rundschnitt im Abstand 1,0d.
 
−
 
−
mit <math>\lambda=\frac{a_{\lambda}}{d}</math>
 
−
und der Bedingung: <math> a_{crit}\le 2d</math>
 
−
Bei Fundamenten ohne vorherrschende Normalspannung und somit einem
 
−
<math>\sigma_{cp} = 0</math>, wird der Nachweis wie folgt geführt:
 
−
<math>\nu_{Ed}\le\nu_{Rd}=C_{Rd,c}\cdot k\cdot (100\cdot f_{ck})^{1/3}\cdot\frac{2d}{a_{crit}}\ge\nu_{min}\cdot\frac{2d}{a_{crit}}</math>(NA)
 
−
 
−
Da bei Fundamenten ein Einfluss der Schlankheit vorherrscht, wird das geforderte
 
−
Zuverlässigkeitsniveau nicht erreicht, folglich muss die Gleichung angepasst
 
−
werden [4]:
 
−
<math>C_{Rd,c}=0,15/\gamma_c</math>
 
−
mit <math>\gamma_c=1,5</math>
 
−
Die Einwirkung setzt sich hierbei folgendermaßen zusammen:
 
−
<math>\nu_{Ed}=\beta\cdot\frac{V_{Ed,red}}{u_{crit\cdot d}}
 
−
mit <math>\beta\le 1,10 (NA)</math>
 
−
 
−
*<math>\beta= 1,10 </math>(NA) für mittige Belastung
 
−
*<math>\beta= 1+k\cdot\frac{M_{Ed}\cdot u_{crit}}{V_{Ed,red}\cdot W}</math>
 
−
 
−
Es besteht somit eine Analogie zwischen dem Nachweis der Durchstanztragfähigkeit
 
−
und der Ermittlung der Querkrafttragfähigkeit bei biegebewehrten Stahlbetonbauteilen.
 
−
Da durch den rotationssymmetrischen Durchstanzkegel eine höhere Rissverzahnung vorliegt, fällt die Durchstanztragfähigkeit jedoch höher aus [2].
 
−
 
−
====Ermittlung des Abstandes acrit====
 
−
In Abhängigkeit des Abstandes acrit kann mit der folgenden Gleichung das maßgebende Minimum ermittelt werden. Somit ergibt sich der relevante kritische Rundschnitt.
 
−
<math>\frac{V_{Rd,c}}{1-\frac{A_{cont}}{A_F}}</math>
 
−
Neben der aufwendigen iterativen Methode zur Ermittlung von acrit bietet das aufgezeigte Diagramm (siehe Bild 15) eine alternative Bestimmungsoption. Dieses stellt die Zusammenhänge der folgenden Eingangsparameter dar [3]:
 
−
<math>\frac{c}{d} und \frac{l}{c}</math>
 
−
mit
 
−
*l- Fundamentlänge
 
−
*c- Stützenbreite
 
−
*d- statische Nutzhöhe
 
−
 
−
====Ausmittig belastete Fundamente mit klaffenden Fugen im Rundschnittbereich====
 
−
In diesem Fall <math>(e = l/6)</math> sollte die Berechnung über einzelne Sektoren erfolgen. Der abzuziehende Wert für den Sohldruck ergibt sich somit für jeden Sektor separat [9].
 
−
 
−
===Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung===
 
−
 
−
Ist der Bemessungswert der Einwirkung <math>\nu_{Ed} größer als der Widerstand <math>\nu_{Rd,c}</math> so ist eine Durchstanzbewehrung auszuführen. Bei dem so entstandenen räumlichen Fachwerkmodell werden die Zugstreben von der Durchstanzbewehrung gebildet [4]. Die möglichen Versagensmechanismen müssen durch mehrere Nachweise geprüft werden. Die Maximaltragfähigkeit <math>\nu_{Rd,max}</math> wird benötigt, um die ausreichende Bewehrungsmenge zu ermitteln. Dieser Wert bezieht sich auf den kritischen Rundschnitt u1 und sagt aus, ob die Einwirkung <math>\nu_{Ed}</math> durch eine Durchstanzbewehrung aufgenommen werden kann [5].
 
−
 
−
<math>\nu_{Ed,u1}=\beta\cdot\frac{V_{Ed}}{u_1\cdot d} \le\nu_{Rd,max}=1,4\cdot\nu_{Rd,c,u1}</math>(NA)
 
−
Bei der Berechnung von <math>\nu_{Rd,c}</math> darf in diesem Fall keine Betondrucknormalspannung <math>\sigma_{cp}</math> durch eine Vorspannung berücksichtig werden [2].
 
−
 
−
Der Nachweis der Durchstanzbewehrung erfolgt ebenfalls für den kritischen Rundschnitt u1. Die so ermittelte Bewehrung wird auf mehrere Rundschnitte verteilt:
 
−
<math>\nu_{Rd,cs}=0,75\cdot\nu_{Rd,c}+1,5\cdot\frac{d}{s_r}\cdot\frac{A_{sw}\cdot f_{ywd,ef\cdot \sin (\alpha)}}{u_1\cdot d}\ge\nu_{u_1}</math>(NA)
 
−
 
−
Hieraus ergibt sich die erforderliche Durchstanzbewehrung:
 
−
<math>A_{swJ}=\kappa_{swJ}\cdot\frac{(\nu_{Ed}-0,75\cdot \nu_{Rd,c})\cdot d \cdot u_1}{1,5\cdot\frac{d}{s_r}\cdot f_{ywd,ef}}</math>
 
−
mit <math> f_{fwd,ef}=250+0,25\cdot d\le f_{ywd}</math> in N/mm^2
 
  
 
==Quellen==
 
==Quellen==
 
<references />
 
<references />
  
−
{{Seiteninfo(mb)
+
 
−
|Quality-flag = [[File:quality-flag-white.gif|right|70px]]
+
{{Seiteninfo
−
|Status = in Bearbeitung|
+
|Quality-flag = [[File:quality-flag-green.gif|right|70px]]
−
|Modul-Version = 2015.0240}}
+
|Status = Seite geprüft, inhaltlich OK|}}

Aktuelle Version vom 27. Oktober 2019, 19:29 Uhr


Allgemeines zum Durchstanzen

Wird eine konzentrierte Last auf eine verhältnismäßig kleine Einleitungsfläche eines Plattentragwerks (z. B. Deckenplatte oder Fundament) aufgebracht, so kommt es zu einem örtlichen Querkraftversagen [1].
Dies äußert sich bei relativ geringen Lasten zunächst durch auftretende Biegerisse in radialer Richtung. Wird die Last erhöht, so kommt es als Folge dessen zum Reißen des Betons in tangentialer Richtung (Querkraftrisse).
Durch die Vereinigung beider Rissformen zu Durchstanzrissen wird der Bruch eingeleitet. [2].
Dabei wird der betroffene Plattenbereich aus der übrigen Platte herausgetrennt und es entsteht der typische kegel- oder pyramidenförmige Körper. Diese Art des Versagens geschieht ohne eine ausgeprägte Vorankündigung. Es kommt zu einem fortschreitenden Kollaps der vollständigen Konstruktion [3].
Folglich ist der Nachweis einer ausreichenden Durchstanztragfähigkeit eines der maßgebenden Kriterien bei der Bemessung einer punktgestützten bzw. durch Einzellasten beanspruchten Deckenplatte. Da das Durchstanzen ein Sonderfall der Querkraftbeanspruchung darstellt, besteht ein Zusammenhang zwischen beiden Bemessungsansätzen [4].

Obwohl das Durchstanz- und das Biegetragverhalten sich gegenseitig beeinflussen (siehe Bild), sind die Nachweise jeweils separat zu führen. [5].

Rissbilder bei reiner Querkraft- und reiner Biegebeanspruchung


Die Durchstanztragfähigkeit wird durch Bauteileigenschaften wie

  • die Betonfestigkeit,
  • die Querschnittabmessungen,
  • die Bewehrungsmenge in der Zugzone,
  • eine durch Vorspannung entstehende Normaldruckkraft und
  • die vorgesehene Durchstanzbewehrung maßgebend beeinflusst [6].


Bei der Nachweisführung müssen folgende Versagen verursachende Komponenten einbezogen werden [2]:

  • eine Überschreitung der Betonzugfestigkeit,
  • ein Versagen der Betondruckzone,
  • ein örtliches Verbundversagen der Biegezugbewehrung
  • und eine unzureichende Verankerung der Durchstanzbewehrung



Der allgemein zu führende Nachweis besagt, dass die auf einen Rundschnitt (besser: die Rundschnittfläche) bezogene einwirkende Querkraft geringer ausfällt, als der Bemessungswiderstand .

Der allgemeine Nachweis lautet wie folgt:


wobei


- Bemessungswert der einwirkenden Querkraft je Flächeneinheit im betrachteten Rundschnitt
- Bemessungswert des Durchstanzwiderstandes je Flächeneinheit im betrachteten Rundschnitt


Bei der Ermittlung des Durchstanzwiderstandes unterscheidet man

  • Bauteile ohne Durchstanzbewehrung
  • Bauteile mit Durchstanzbewehrung


Bemessungswert der einwirkenden Querkraft


Genauere Informationen zur Ermittlung des Bemessungswertes der einwirkenden Querkraft finden Sie hier: Durchstanzen - Bemessungswert der einwirkenden Querkraft

Bauteile ohne Durchstanzbewehrung

Versagensmechanismus bei einem Bauteil ohne Durchstanzbewehrung

Bei Plattentragwerken ohne Durchstanzbewehrung (siehe Bild) muss nachgewiesen werden, dass der Bemessungswert der einwirkenden Querkraft im kritischen Rundschnitt den Bemessungswert der Durchstanztragfähigkeit ohne Durchstanzbewehrung nicht überschreitet.
Die Bedingung lautet:


wobei


- Bemessungswert der einwirkenden Querkraft je Flächeneinheit im kritischen Rundschnitt
- Bemessungswert des Durchstanzwiderstandes je Flächeneinheit einer Platte ohne Durchstanzbewehrung


Ist der Bemessungswiderstand größer als der Bemessungswert der Querkraft , so ist eine Durchstanzbewehrung vorzusehen, welche beispielsweise durch Bügel gebildet werden kann. Alternativ kann auch durch das Vergrößern der Längsbewehrung die Durchstanztragfähigkeit gesteigert werden.

Genauere Informationen zum Nachweis für Bauteile ohne Durchstanzbewehrung : Punktförmig gestützte Platten und Fundamente ohne Durchstanzbewehrung

Bauteile mit Durchstanzbewehrung

Wird Durchstanzbewehrung benötigt, so muss auf mehreren Rundschnitten ui weitere Querkraftnachweise geführt werden[2].

Versagensmechanismus bei Bauteilen mit Durchstanzbewehrung


Als Durchstanzbewehrung können folgende Bewehrungselemente zum Einsatz kommen:

  • Bügel
  • aufgebogene Stäbe
  • S-Haken
  • Dübelleisten
  • spezielle Gitterträger

Je nach verwendeter Durchstanzbewehrung sind beim Verlegen der Bewehrung weitere Regel zu beachten.
Beim Nachweis von Bauteilen mit Durchstanzbewehrung sind folgende Einzelnachweise zu führen (siehe Bild) [2]:

  • Betonversagen: die maximale Schubspannung darf nicht größer ausfallen, als der Bemessungswert des maximalen Durchstanzwiderstands .



  • Stahlversagen: die Tragfähigkeit des Querschnitts mit Durchstanzbewehrung muss in jedem Rundschnitt gewährleistet sein.



  • Querkrafttragfähigkeit ohne Durchstanzbewehrung: außerhalb des durchstanzbewehrtem Bereichs muss die Querkrafttragfähigkeit ohne Durchstanzbewehrung nachgewiesen werden.



Genauere Informationen zu dem Nachweis für Bauteile mit Durchstanzbewehrung: Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung

Beispiel: Berechnung einer Flachdecke mit einer Rundstütze

Ein Berechnungsbeispiel findet man auf der Seite: Flachdecke mit einer Rundstütze (Bsp.)

Quellen

  1. ↑ K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012
  2. ↑ 2,0 2,1 2,2 2,3 Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012
  3. ↑ Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012
  4. ↑ Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012
  5. ↑ Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript
  6. ↑ Prof Dr.-Ing. Guido Bolle. Skript: Modul - Stahlbetonbau 2


Seiteninfo
Quality-flag-green.gif
Status: Seite geprüft, inhaltlich OK
Abgerufen von „https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php?title=Durchstanzen&oldid=10733“