|
|
| (74 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | + | |
| | + | <br /> |
| | + | |
| | ==Allgemeines zum Durchstanzen== | | ==Allgemeines zum Durchstanzen== |
| | | | |
| − | Wird eine '''konzentrierte Last''' auf eine verhältnismäßig '''kleine Einleitungsfläche''' eines Plattentragwerks (z.B. Deckenplatte oder Fundament) aufgebracht, so kommt | + | Wird eine ''konzentrierte Last'' auf eine verhältnismäßig ''kleine [[Durchstanzen - Lasteinleitungsfläche und kritischer Rundschnitt|Einleitungsfläche]]'' eines Plattentragwerks (z. B. Deckenplatte oder Fundament) aufgebracht, so kommt |
| − | es zu einem '''örtlichen Querkraftversagen''' | + | es zu einem ''örtlichen Querkraftversagen'' |
| | <ref name = "Q1">K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref>.<br /> | | <ref name = "Q1">K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref>.<br /> |
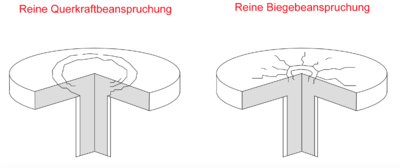
| − | Dies äußert sich bei relativ geringen Lasten durch auftretende Biegerisse in radialer Richtung. Wird die Last erhöht, so kommt es als Folge dessen zum Reißen des Betons in tangentialer Richtung (Querkraftrisse). <br /> | + | Dies äußert sich bei relativ geringen Lasten zunächst durch auftretende Biegerisse in radialer Richtung. Wird die Last erhöht, so kommt es als Folge dessen zum Reißen des Betons in tangentialer Richtung (Querkraftrisse). <br /> |
| − | Durch die Vereinigung zu Durchstanzrissen verursachen diese einen '''Bruch''' | + | Durch die Vereinigung beider Rissformen zu Durchstanzrissen wird der ''Bruch'' eingeleitet. |
| | <ref name = "Q2">Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>. | | <ref name = "Q2">Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012</ref>. |
| | <br /> | | <br /> |
| − | Trennt sich der betroffenen Plattenbereich heraus, so entsteht der typische kegel- oder pyramidenförmige Körper. Diese Art des Versagens geschieht ohne eine ausgeprägte
| + | Dabei wird der betroffene Plattenbereich aus der übrigen Platte herausgetrennt und es entsteht der typische kegel- oder pyramidenförmige Körper. Diese Art des Versagens geschieht ohne eine ausgeprägte Vorankündigung. Es kommt zu einem fortschreitenden Kollaps der vollständigen Konstruktion |
| − | Vorankündigung. Es kommt zu einem fortschreitenden Kollaps der vollständigen Konstruktion | |
| | <ref name = "Q3">Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012</ref>. | | <ref name = "Q3">Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012</ref>. |
| | <br /> | | <br /> |
| − | Folglich ist diese Art von Nachweis das '''maßgebende''' '''Kriterium bei der Bemessung einer Deckenplatte'''. Da das Durchstanzversagen ein Sonderfall der Querkraftbeanspruchung darstellt, besteht ein Zusammenhang zwischen | + | Folglich ist der Nachweis einer ausreichenden Durchstanztragfähigkeit eines der ''maßgebenden Kriterien '' bei der Bemessung einer punktgestützten bzw. durch Einzellasten beanspruchten Deckenplatte. Da das Durchstanzen ein Sonderfall der Querkraftbeanspruchung darstellt, besteht ein Zusammenhang zwischen beiden Bemessungsansätzen |
| − | beiden Bemessungsansätzen | |
| | <ref name = "Q4">Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012</ref>. | | <ref name = "Q4">Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012</ref>. |
| | | | |
| − | Obwohl die Durchstanztragfähigkeit und das Biegetragverhalten sich gegenseitig beeinflussen (siehe Bild 1), sind ihre Berechnung separat durchzuführen. <ref name = "Q5">Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript</ref>. | + | Obwohl das Durchstanz- und das Biegetragverhalten sich gegenseitig beeinflussen (siehe Bild), sind die Nachweise jeweils separat zu führen. <ref name = "Q5">Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript</ref>. |
| | <br /> | | <br /> |
| − | <br />
| + | [[Datei:Durchstanzen_1.png|400px|thumb|right| Rissbilder bei reiner Querkraft- und reiner Biegebeanspruchung ]] |
| − | [[Datei:Durchstanzen_1.png|400px|thumb|right|Bild 1: Rissbilder bei reiner Querkraft- und reiner Biegebeanspruchung ]] | |
| | | | |
| | | | |
| − | Die '''Durchstanztragfähigkeit''' wird durch Bauteileigenschaften wie | + | Die ''Durchstanztragfähigkeit'' wird durch Bauteileigenschaften wie |
| − | <br />
| |
| − | <br />
| |
| − | *der '''Betonfestigkeit''',
| |
| − | *den '''Querschnittabmessungen''',
| |
| − | *der '''Bewehrungsmenge in der Zugzone''',
| |
| − | *eine durch Vorspannung entstehende '''Normaldruckkraft''' und
| |
| − | *die vorgesehene '''Durchstanzbewehrung''' maßgebend beeinflusst <ref name = "Q6">Prof Dr.-Ing. Guido Bolle. Skript: Modul - Stahlbetonbau 2</ref>.
| |
| − | <br />
| |
| − | Bei der Nachweisführung müssen folgende '''Versagen verursachende Komponenten''' einbezogen werden <ref name="Q2" />:
| |
| − | <br />
| |
| − | <br />
| |
| − | *eine '''Überschreitung der Betonzugfestigkeit''',
| |
| − | *ein '''Versagen der Betondruckzone''',
| |
| − | *ein '''örtliches Verbundversagen''' der Biegezugbewehrung
| |
| − | *und eine '''unzureichende Verankerung''' der Durchstanzbewehrung
| |
| − | <br />
| |
| − | <br />Der zu führende Nachweis besagt, dass die auf den kritischen Rundschnitt <math> d \cdot u </math> bezogene einwirkende Querkraft <math>\nu_ {Ed}</math> geringer ausfällt, als der Bemessungswiderstand <math>\nu_{Rd}</math>.
| |
| − | <br />
| |
| − | Der '''Nachweis''' lautet wie folgt:
| |
| − | <br />
| |
| − | <br />
| |
| − | <math>\nu_ {Ed}=\beta \cdot \frac{V_{Ed}}{u_i \cdot d} \leq \nu_ {Rd}</math>
| |
| | <br /> | | <br /> |
| | + | *die ''Betonfestigkeit'', |
| | + | *die ''Querschnittabmessungen'', |
| | + | *die ''Bewehrungsmenge in der Zugzone'', |
| | + | *eine durch Vorspannung entstehende ''Normaldruckkraft'' und |
| | + | *die vorgesehene ''Durchstanzbewehrung'' maßgebend beeinflusst <ref name = "Q6">Prof Dr.-Ing. Guido Bolle. Skript: Modul - Stahlbetonbau 2</ref>. |
| | <br /> | | <br /> |
| − | Es findet hierbei eine Unterscheidung in Bauteilen mit und ohne Durchstanzbewehrung statt.
| + | Bei der Nachweisführung müssen folgende ''Versagen verursachende Komponenten'' einbezogen werden <ref name="Q2" />: |
| | <br /> | | <br /> |
| | + | *eine ''Überschreitung der Betonzugfestigkeit'', |
| | + | *ein ''Versagen der Betondruckzone'', |
| | + | *ein ''örtliches Verbundversagen'' der Biegezugbewehrung |
| | + | *und eine ''unzureichende Verankerung'' der Durchstanzbewehrung |
| | <br /> | | <br /> |
| | + | <br />Der allgemein zu führende Nachweis besagt, dass die auf einen [[Durchstanzen - Lasteinleitungsfläche und kritischer Rundschnitt|Rundschnitt]] <math> d \cdot u </math> (besser: die Rundschnittfläche) bezogene einwirkende Querkraft <math>\nu_ {Ed}~</math> geringer ausfällt, als der Bemessungswiderstand <math>\nu_{Rd}~</math>.<br /> |
| | <br /> | | <br /> |
| | | | |
| − | ==Bauteile ohne Durchstanzbewehrung==
| + | Der ''allgemeine Nachweis'' lautet wie folgt: |
| − | [[Datei:Durchstanzen_2.png|300px|thumb|right|Bild 2: Versagensmechanismus bei einem Bauteil ohne Durchstanzbewehrung ]]
| |
| − | Bei Plattentragwerken ohne Durchstanzbewehrung (siehe Bild 2) muss der folgende Nachweis klären, ob die Tragfähigkeit des Betons im kritischen Rundschnitt ausreichend ist und die auftretende Querkraft den Bauteilwiderstand somit nicht überschreitet <ref name="Q2" />.
| |
| − | <br />
| |
| − | <br />
| |
| − | Im Allgemeinen gilt:
| |
| − | <br />
| |
| | <br /> | | <br /> |
| | :<math> \nu_ {Ed}\leq\nu_ {Rd}</math> | | :<math> \nu_ {Ed}\leq\nu_ {Rd}</math> |
| | <br /> | | <br /> |
| − | Somit muss bei Bauteilen ohne Durchstanzbewehrung die Querkrafttragfähigkeit des Betons im kritischen Rundschnitt größer sein, als die vorherrschende Einwirkung:
| |
| − | <br />
| |
| − | <br />
| |
| − | :<math> \nu_ {Ed}\leq\nu_ {Rd,c}</math>
| |
| − | <br />
| |
| − | Ist der Bemessungswiderstand <math>\nu_ {Ed}</math> größer als der Bemessungswert der Querkraft <math>\nu_ {Rd}</math> , so ist eine Durchstanzbewehrung vorzusehen, welche beispielsweise durch Bügel gebildet werden kann.<br />
| |
| − | Ist diese Maßnahme nicht ausreichend, können tragfähigkeitserhöhende Einbauteile vorgesehen werden<ref name="Q4" />.
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − |
| |
| − | ==Bauteile mit Durchstanzbewehrung==
| |
| | | | |
| − | Wird Durchstanzbewehrung benötigt, so muss auf mehreren Rundschnitten u<sub>i</sub> weitere Querkraftnachweise geführt werden<ref name="Q2" />.
| + | :wobei |
| − | <br />
| |
| − | [[Datei:Durchstanzen_3.png|300px|thumb|right|Bild 3: Versagensmechanismus bei Bauteilen mit Durchstanzbewehrung ]]
| |
| − | <br />
| |
| − | Des Weiteren kann zur Steigerung der Tragfähigkeit zusätzlich zur Durchstanzbewehrung eine Querkraftbewehrung in Form von aufgebogenen Stäben, Bügeln, S-Haken oder Dübelleisten in Betracht gezogen werden. Werden solche verwendet, ist eine zweite Reihe an Schubbewehrung anzuordnen, auch wenn diese rechnerisch
| |
| − | nicht erforderlich ist<ref name = "Q7">Dipl.-Ing. Klaus Beer. Bewehren nach DIN EN 1992-1-1(EC2). Vieweg+Teubner, S. 196-207, 3. Aufl. edition, 2012</ref>. Bei der Ausführung von Durchstanzbewehrung müssen mehrere Versagensmechanismen (siehe Bild 3) betrachtet werden [2]:
| |
| − | <br />
| |
| − | <br />
| |
| − | '''Betonversagen:''' die maximale Schubspannung <math>\nu_ {Rd,Ed}</math> nach Gleichung (1) darf nicht größer ausfallen, als der Bemessungswert des maximalen Durchstanzwiderstands <math>\nu_ {Rd,max}</math>.
| |
| − | <br />
| |
| − | <br />
| |
| − | :<math> \nu_ {Ed}\leq\nu_ {Rd,max}</math>
| |
| − | <br />
| |
| − | <br />
| |
| − | '''Stahlversagen:''' die Tragfähigkeit des Querschnitts mit Durchstanzbewehrung muss in jedem Rundschnitt gewährleistet sein.
| |
| − | <br />
| |
| − | <br />
| |
| − | :<math>\nu_ {Ed}\leq\nu_ {Rd,cs}</math>
| |
| − | <br />
| |
| − | <br />
| |
| − | Die Querkrafttragfähigkeit muss in der Umgebung '''außerhalb des durchstanzbewehrtem Bereichs ohne Querkraftbewehrung''' gegeben sein.
| |
| − | <br />
| |
| − | <br />
| |
| − | :<math>\nu_ {Ed}\leq\nu_ {Rd,c,out}</math>
| |
| | <br /> | | <br /> |
| | | | |
| − | ==Lasteinleitungsfläche und kritischer Rundschnitt==
| + | ::<math>\nu_ {Ed}~</math> - Bemessungswert der einwirkenden Querkraft je Flächeneinheit im betrachteten Rundschnitt |
| − | <br />
| + | ::<math>\nu_ {Rd}~</math> - Bemessungswert des Durchstanzwiderstandes je Flächeneinheit im betrachteten Rundschnitt |
| − | [[Datei:Durchstanzen_4.png|400px|thumb|right|Bild 4: Kritischer Rundschnitt bei variablen Geometrien ]]
| |
| − | Die Bemessung der '''Lasteinleitungsfläche A<sub>load</sub>''' mit dem kritischen Rundschnitt u<sub>1</sub> gilt für folgende Geometrien:<br />
| |
| − | *Rundstützen mit dem Umfang <math>u_0 \leq 12d</math>
| |
| − | *Rechteckstützen mit <math>u_0 \leq 12d</math> und dem Verhältnis von Länge zu Breite<math> \leq 2</math>
| |
| − | *andere Formen, die sinnvoll wie oben genannt begrenzt werden können
| |
| − | <br />
| |
| − | <br />
| |
| − | Dabei wird die benötigte '''statische Nutzhöhe d''' wie folgt ermittelt:
| |
| − | <br />
| |
| − | <br />
| |
| − | <math> \frac{(d_x+d_y)}{2}</math> | |
| − | [[Datei:Durchstanzen_5.png|300px|thumb|right|Bild 5: Bezeichnungen am kritischen Rundschnitt ]]
| |
| − | [[Datei:Durchstanzen_6.png|300px|thumb|right|Bild 6: Draufsicht eines kritischen Rundschnitts]]
| |
| − | <br />
| |
| − | Die Lasteinleitungsfläche darf sich nicht in der Nähe von anderen konzentrierten Lasten sowie anderen wirkenden Querkräften befinden, was eine Überschneidung der kritischen Rundschnitte zur Folge hätte<ref name="Q1" />.<br />
| |
| − | Ist dies dennoch der Fall, so ist im Durchstanznachweis der gesamte Rundschnittumfang mit der kleinsten Umhüllenden unter Berücksichtigung der Umfangsbegrenzung der Lasteinleitungsfläche von 12d in Ansatz zu bringen (Nationaler Anhang (NA)) <ref name="Q2" />. <br />
| |
| − | Einwirkung und Widerstand werden auf den kritischen Rundschnitt bezogen, dieser wird bei Rund- und Rechteckstützen im Abstand 2d von der Lasteinleitungsfläche gebildet (siehe Bild 4) <ref name="Q5" />.
| |
| − | <br />
| |
| − | Die kritische Fläche A<sub>cont</sub> stellt die Fläche innerhalb des kritischen Rundschnitts u<sub>1</sub> dar (siehe Bild 5 und 6) .
| |
| − | <br />
| |
| − | Bei der Ermittlung des kritischen Rundschnitts sind einspringende Ecken zu überlesen, da der kleinste aller Rundschnitte maßgebend ist <ref name="Q5" />. <br />
| |
| − | Die Berücksichtigung eines Rundschnitts kleiner als 2d ist dann notwendig, wenn ein großer Gegendruck beispielsweise durch Sohldruck bei Fundamenten, einer Auflagerreaktion oder einer Last innerhalb des kritischen Rundschnitts (2d) vorherrscht.
| |
| − | Trifft dieser Fall zu, so ist der Abstand a<sub>crit</sub> iterativ zu ermitteln (NA) <ref name="Q2" />. Sind die oben genannten Bedingungen in Bezug auf die rechteckige Lasteinleitungsfläche nicht erfüllt, so darf nur ein reduzierter kritischer Rundschnitt in Ansatz gebracht werden <ref name="Q4" />.
| |
| − | <br />
| |
| | <br /> | | <br /> |
| | + | Bei der Ermittlung des Durchstanzwiderstandes <math>\nu_{Rd}~</math> unterscheidet man |
| | + | * Bauteile ohne Durchstanzbewehrung |
| | + | * Bauteile mit Durchstanzbewehrung |
| | <br /> | | <br /> |
| | | | |
| | + | ==Bemessungswert der einwirkenden Querkraft== |
| | <br /> | | <br /> |
| − | <br />
| + | Genauere Informationen zur Ermittlung des Bemessungswertes der einwirkenden Querkraft finden Sie hier: [[Durchstanzen - Bemessungswert der einwirkenden Querkraft]] |
| − | <br />
| |
| − | <br />
| |
| − | ===Ausgedehnte Einleitungsflächen===
| |
| − | <br />
| |
| − | [[Datei:Durchstanzen_7.png|300px|thumb|left|Bild 7: Kritischer Rundschnitt bei ausgedehnten Einbeitungsflächen ]] | |
| − | Ist das Seitenverhältnis <math>a/b > 2 </math> oder der Umfang der Lasteinleitungsfläche <math>A_{load} > 12d</math>, so müssen gesonderte Nachweise geführt werden, <br />
| |
| − | welche nur auf Teilrundschnitte mit <math>u_0 \ge 12d</math> zu beziehen sind (siehe Bild 7).<br />
| |
| − | Der Querkraftwiderstand ist für alle weiteren, über den Umfang hinaus ragenden Bereiche zu ermitteln. <br />
| |
| − | Die Summe aus der Durchstanztragfähigkeit sowie der Querkrafttragfähigkeit bildet den Gesamtwiderstand <ref name="Q5" />.
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| | | | |
| − | ===Randnähe=== | + | ==Bauteile ohne Durchstanzbewehrung== |
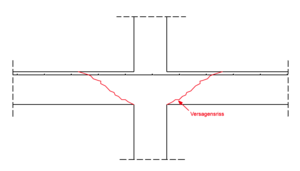
| − | [[Datei:Durchstanzen_8.png|120px|thumb|left|Bild 8: Kritischer Rundschnitt in Randnähe ]] | + | [[Datei:Durchstanzen_2.png|300px|thumb|right|Versagensmechanismus bei einem Bauteil ohne Durchstanzbewehrung ]] |
| − | <br />
| + | Bei Plattentragwerken ohne Durchstanzbewehrung (siehe Bild) muss nachgewiesen werden, dass der Bemessungswert der einwirkenden Querkraft im kritischen Rundschnitt den Bemessungswert der Durchstanztragfähigkeit ohne Durchstanzbewehrung nicht überschreitet. |
| − | Liegt die Lasteinleitungsfläche nahe eines freien Randes, so ist der minimale kritische Rundschnitt möglicherweise nicht mehr geschlossen und endet in diesem Fall stets orthogonal zu diesem <ref name="Q5" />. <br />
| |
| − | Im zutreffenden Fall ist der Rundschnitt wie in Bild 8 aufgezeigt anzunehmen.
| |
| − | Dieser Rundschnitt wird jedoch nur maßgebend, wenn der Umfang kleiner ist als der des "Regelrundschnitts" bei geschlossener Schnittführung <ref name= "Q8">G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010</ref>.<br />
| |
| − | Beträgt der Abstand zum freien Rand < d, so ist in der Regel eine besondere Randbewehrung einzulegen <ref name="Q1" />.
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| | <br /> | | <br /> |
| | + | Die Bedingung lautet: |
| | <br /> | | <br /> |
| | + | :<math> \nu_ {Ed}\leq\nu_ {Rd,c}</math> |
| | <br /> | | <br /> |
| | | | |
| − | ===Öffnungen===
| + | :wobei |
| − | [[Datei:Durchstanzen_9.png|200px|thumb|left|Bild 9: Kritischer bei Öffnungen ]]
| |
| − | <br />
| |
| − | Liegt der Rand der Lasteinleitungsfläche im Abstand < 6d von einer Öffnung entfernt, so muss die der Öffnung zugewandte Seite des Rundschnitts als unwirksam betrachtet werden.<br />
| |
| − | Diese ist somit bei der Berechnung abzuziehen <ref name= "Q9">Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchstanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009</ref>.
| |
| − | Der Umfang lässt sich somit wie in Bild 9 dargestellt bilden.
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| | <br /> | | <br /> |
| | | | |
| − | ==Bemessungswert der Einwirkung==
| + | ::<math>\nu_ {Ed}~</math> - Bemessungswert der einwirkenden Querkraft je Flächeneinheit im kritischen Rundschnitt |
| − | <br />
| + | ::<math>\nu_ {Rd,c}~</math> - Bemessungswert des Durchstanzwiderstandes je Flächeneinheit einer Platte ohne Durchstanzbewehrung |
| − | Die als Spannung angegebene Bemessungsquerkraft bezieht sich auf die Querschnittsfläche
| |
| − | des kritischen Rundschnitts <ref name="Q5" />.
| |
| − | <br />
| |
| − | Die Gleichung dafür lautet:
| |
| − | <br />
| |
| − | <br />
| |
| − | :<math>\nu_ {Ed}=\beta \cdot \frac{V_{Ed}}{u_i \cdot d} </math> | |
| − | <br />
| |
| − | <br />
| |
| − | ==Korrekturfaktor β ==
| |
| − | - nach EC 2-1-1, 6.4.3.(6) | |
| − | <br /> | |
| − | Infolge von Biegung ist die aufgebrachte Querkraft nicht mehr gleichmäßig über den Umfang verteilt, die Belastung einer Seite ist folglich erhöht. Der '''Lasterhöhungsfaktor β''' berücksichtigt diesen Umstand<ref name="Q5" />.<br />
| |
| − | Zur Ermittlung des Faktors β stehen '''drei Verfahren''' zur Verfügung. <br />
| |
| − | Diese werden folgend erläutert:
| |
| − | <br />
| |
| | <br /> | | <br /> |
| | | | |
| − | ===Konstanter Faktor für ausgesteifte Systeme mit nahezu gleichen Stützweiten===
| + | Ist der Bemessungswiderstand <math>\nu_ {Ed}~</math> größer als der Bemessungswert der Querkraft <math>\nu_ {Rd,c}~</math> , so ist eine Durchstanzbewehrung vorzusehen, welche beispielsweise durch Bügel gebildet werden kann. Alternativ kann auch durch das Vergrößern der Längsbewehrung die Durchstanztragfähigkeit gesteigert werden.<br /> |
| − | <br />
| |
| − | Es werden horizontal unverschiebliche, ausgesteifte Systeme mit Stützweitenunterschieden
| |
| − | von maximal 25 % und eine Belastung durch Gleichlast angenommen <ref name="Q7" />. Die Stützweitenverhältnisse betragen somit <math>0,8\leq l_1/l_2\leq 1,25</math> <ref name="Q8" />.
| |
| − | [[Datei:Durchstanzen_10.png|300px|thumb|right|Bild 10: Korrekturfaktor Beta ]]
| |
| − | <br />
| |
| − | <br />
| |
| − | Für diesen Fall können somit folgende '''konstante Näherungswerte''' angenommen werden(siehe Bild 10):
| |
| − | <br />
| |
| − | *1,10 Innenstützen
| |
| − | *1,40 Randstützen
| |
| − | *1,35 Wandenden (NA)
| |
| − | *1,50 Eckstützen
| |
| − | *1,20 Wandecken (NA)
| |
| − | *Bei Fundamenten wird ein <math> \beta \leq 1,10</math> angenommen.
| |
| − | <br /> | |
| | <br /> | | <br /> |
| | + | Genauere Informationen zum Nachweis für Bauteile ohne Durchstanzbewehrung : [[Durchstanzen - Punktförmig gestützte Platten und Fundamente ohne Durchstanzbewehrung|Punktförmig gestützte Platten und Fundamente ohne Durchstanzbewehrung]] |
| | | | |
| − | ===Ermittlung über Sektormodell=== | + | ==Bauteile mit Durchstanzbewehrung== |
| − | <br />
| |
| − | Im ersten Schritt sind die Querkraftnulllinien anzusätzen. Diese werden abgeschätzt
| |
| − | oder errechnet (linear-elastisch). Anschließend findet eine Unterteilung
| |
| − | der Lasteinzugsfläche <math>A_{LE}</math> in i-Lasteinleitungssektoren <math>A_i</math> (siehe Bild 11) statt.
| |
| − | [[Datei:Durchstanzen_11.png|300px|thumb|right|Bild 11: Sektormodell ]]
| |
| − | Hierbei sollten mindestens 3-4 Sektoren pro Quadrant betrachtet werden <ref name="Q1" />.<br />
| |
| − | Der Lasterhöhungsfaktor ergibt sich somit wie folgt <ref name="Q2" />:
| |
| − | <br />
| |
| − | :<math> \nu_{Ed}=e_d \cdot A_{LE}</math>
| |
| − | <br />
| |
| − | :<math> \nu_{Ed,m}=\nu_Ed \cdot u_{crit}</math>
| |
| − | <br />
| |
| − | :<math> \nu_{Ed,i}=e_d \cdot \frac{A_i}{u_i}</math>
| |
| − | <br />
| |
| − | :<math> \beta=max\{ \nu_{Ed,i}/\nu_{Ed,m}\}</math>
| |
| − | <br />
| |
| − | <br />
| |
| | | | |
| − | ===Genaueres Verfahren=== | + | Wird Durchstanzbewehrung benötigt, so muss auf mehreren Rundschnitten u<sub>i</sub> weitere Querkraftnachweise geführt werden<ref name="Q2" />. |
| − | | |
| − | nach EC 2-1-1, 6.4.3 (1;2)
| |
| | <br /> | | <br /> |
| − | Sind die oben genannten Voraussetzungen nicht erfüllt oder ist die bezogene Ausmitte <math>e/c</math> bei Randstützen größer als 1,2 (wobei c die Stützenabmessung in Richtung der Ausmitte darstellt), ist der Lasterhöhungsfaktor mit genaueren Verfahren
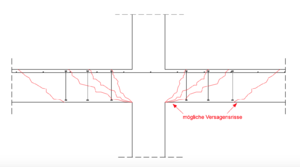
| + | [[Datei:Durchstanzen_3.png|300px|thumb|right|Versagensmechanismus bei Bauteilen mit Durchstanzbewehrung ]] |
| − | [[Datei:Durchstanzen_12.png|300px|thumb|left|Bild 12: Querkraftverteilung infolge eines Kopfmomentes einer Stütze ]] | |
| − | zu ermitteln. Hierbei wird die Annahme einer vollplastischen Schubspannungsverteilung am kritischen Rundschnitt getroffen <ref name="Q4" />.
| |
| | <br /> | | <br /> |
| | + | Als Durchstanzbewehrung können folgende Bewehrungselemente zum Einsatz kommen: |
| | + | * Bügel |
| | + | * aufgebogene Stäbe |
| | + | * S-Haken |
| | + | * Dübelleisten |
| | + | * spezielle Gitterträger |
| | + | Je nach verwendeter Durchstanzbewehrung sind beim Verlegen der Bewehrung weitere Regel zu beachten. |
| | <br /> | | <br /> |
| − | Die Gleichung lautet somit wie folgt:
| + | Beim Nachweis von Bauteilen mit Durchstanzbewehrung sind folgende Einzelnachweise zu führen (siehe Bild) <ref name="Q2" />: |
| | <br /> | | <br /> |
| − | :<math>\beta=1+k\cdot\frac{M_{Ed}}{V_{Ed}}\cdot\frac{u_1}{W_1}\le 1,10</math><br /> | + | * ''Betonversagen:'' die maximale Schubspannung <math>\nu_ {Rd,Ed}</math> darf nicht größer ausfallen, als der Bemessungswert des maximalen Durchstanzwiderstands <math>\nu_ {Rd,max}</math>. |
| − | mit<br />
| |
| | <br /> | | <br /> |
| − | :<math> W_1=\int_0^{u_i} |e| dl</math><br /> | + | ::<math> \nu_ {Ed}\leq\nu_ {Rd,max}</math> |
| | <br /> | | <br /> |
| − | und somit bei einer geschlossenen Rechteckstütze mit c1 parallel und c2 senkrecht zur Lastausmitte:<br />
| + | * ''Stahlversagen:'' die Tragfähigkeit des Querschnitts mit Durchstanzbewehrung muss in jedem Rundschnitt gewährleistet sein. |
| | <br /> | | <br /> |
| − | :<math>W_1=\frac{c_1^2}{2}+c_1c_2+4c_2d+16d^2+2\pi dc_1</math> | + | ::<math>\nu_ {Ed}\leq\nu_ {Rd,cs}</math> |
| − | | |
| − | | |
| − | <br />
| |
| − | und dem '''Beiwert k'''
| |
| − | [[Datei:Durchstanzen_12a.png|200px|thumb|left|Tabelle Beiwert k ]]<br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | Bei Decken-Stützenknoten mit zweiachsiger Ausmitte gilt (NA) [2]:<br />
| |
| − | <br />
| |
| − | :<math>W_1=1+\sqrt{(k_y\cdot\frac{M_{Ed,y}}{V_{Ed}}\cdot\frac{u_1}{W_{1,y}})^2+(k_z\cdot\frac{M_{Ed,z}}{V_{Ed}}\cdot\frac{u_1}{W_{1,z}})^2}\ge 1,10</math>
| |
| − | <br />
| |
| − | <br />
| |
| − | | |
| − | ==Punktförmig gestützt Platten und Fundamente ohne Durchstanzbewehrung==
| |
| − | | |
| − | Bei Platten ohne Durchstanzbewehrung lautet der erforderliche Nachweis im kritischen
| |
| − | Rundschnitt wie folgt:
| |
| − | <br />
| |
| − | :<math>\nu_{Ed}\le\nu_{Rd,c}=C_{Rd,c}\cdot k\cdot (100\cdot\rho_l\cdot f_{ck})^{^1/3}+k_1 \cdot \sigma_{cp}\ge\nu_{min}+k_1\cdot\sigma_{cp}</math> | |
| − | <br />
| |
| − | Die '''Einflussfaktoren''' sind folglich die Betonfestigkeit, der Längsbewehrungsgrad, die Plattendicke sowie die Betonnormalspannung (z.B. infolge einer Vorspannung).<br />
| |
| − | <br />
| |
| − | Für Flachdecken gilt im Allgemeinen:
| |
| − | <br />
| |
| − | :<math>C_{Rd,c}=0,18/\gamma_c</math><br />
| |
| − | <br />
| |
| − | mit
| |
| − | <br />
| |
| − | <math>\gamma_c=1,5</math>
| |
| − | | |
| − | Dieser empirische Vorwert beträgt für ständige und vorübergehende Bemessungssituationen C<sub>Rd,c</sub>= 0,12.
| |
| − | [[Datei:Durchstanzen_13.png|400px|thumb|right|Bild 13: u0>4d und u0<4d]]
| |
| − | <br />
| |
| − | Für Innenstützen bei Flachdecken mit dem Verhältnis <math>u0/d < 4</math> (mächtige Platte auf schlanker Stütze, siehe Bild 13) gilt (NA) <ref name="Q5" />:
| |
| − | <br />
| |
| − | :<math>C_{Rd,c}=0,18/\gamma_c\cdot (0,1\cdot u_0/d+0,6)</math>
| |
| − | <br />
| |
| − | Bei Rundstützen mit einem <math>u_0\ge 12d</math> ist das <math>C_{Rd,c}</math> wie folgt zu ermitteln, da man von einer querkraftbeanspruchten Flachdecke ausgeht <ref name="Q1" />:
| |
| − | <br />
| |
| − | :<math>C_{Rd,c}=\frac{12d}{u_0}\cdot\frac{0,18}{\gamma_c}\ge\frac{0,15}{\gamma_c}</math>
| |
| − | <br />
| |
| − | <br />
| |
| − | Weitere benötigte Parameter des Nachweises ergeben sich wie folgt:<br />
| |
| − | *'''Maßstabsfaktor''' zur Berücksichtigung der Bauteilhöhe mit d in mm:
| |
| − | <br />
| |
| − | :<math>k=1+\sqrt{\frac{200}{d}}\le 2,0</math>
| |
| − | <br />
| |
| − | *'''Bewehrungsgrad''', bezogen auf die mitwirkende Plattenbreite:
| |
| − | <br />
| |
| − | :<math>\rho_l=\sqrt{\rho_{lx}\cdot\rho_{ly}}\le 0,02</math> und <math>\le 0,50\cdot\frac{f_{cd}}{f_{yd}}</math> (NA)
| |
| − | <br />
| |
| − | *'''Betonnormalspannung''' in N/mm2 (Druck positiv!):
| |
| − | <br />
| |
| − | :<math>\sigma_{cp}=\frac{\sigma_{cx}+\sigma_{cy}}{2}</math>
| |
| − | <br />
| |
| − | *'''Mindesttragfähigkeit''': maßgebend, wenn <math>\nu_{min}\ge\nu_{Rd,c}</math>
| |
| − | <br />
| |
| − | :<math>\nu_{min}=0,035\cdot k^{3/2}\cdot f_{ck}^{1/2}</math>
| |
| − | <br />
| |
| − | :<math>\nu_{min}=(0,0525/\gamma_c)\cdot k^{3/2}\cdot f_{ck}^{1/2}</math> für <math>d\le 600mm</math> (NA)
| |
| − | <br />
| |
| − | :<math>\nu_{min}=(0,0375/\gamma_c)\cdot k^{3/2}\cdot f_{ck}^{1/2}</math> für <math>d> 800mm</math> (NA)
| |
| − | <br />
| |
| − | Für <math>600 mm < d\le 800</math>mm darf interpoliert werden.
| |
| − | <br />
| |
| − | :<math> k_1=0,10</math>
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | ==Stützenkopfverstärkungen==
| |
| − | | |
| − | Eine Stützenkopfverstärkung dient der Erhöhung der Tragfähigkeit, da durch diese der Durchmesser des Durchstanzkegels vergrößert wird <ref name="Q8" />. <br />
| |
| − | ====Schlanker Stützenkopf: l<sub>H</sub>>2,0 ====
| |
| − | [[Datei:Durchstanzen_14b.png|300px|thumb|right|Bild 14a: Stützenkopfverstärkung bei l<sub>H</sub>>2,0 ]]
| |
| − | Der Nachweis ist innerhalb und außerhalb der Stützenkopfverstärkung zu führen.
| |
| − | <br />
| |
| − | <br />
| |
| − | ====Gedrungener Stützenkopf: l<sub>H</sub><2,0====
| |
| − | [[Datei:Durchstanzen_14c.png|300px|thumb|right|Bild 14b: Stützenkopfverstärkung bei l<sub>H</sub><2,0 ]]
| |
| − | In diesem Fall ist der Nachweis nur außerhalb der Stützenkopfverstärkung zu führen.
| |
| − | <br />
| |
| − | <br />
| |
| − | ==== Stützenkopf mit 1,5<l<sub>H</sub><2,0====
| |
| − | [[Datei:Durchstanzen_14a.png|300px|thumb|right|Bild 14c: Stützenkopfverstärkung bei 1,5<l<sub>H</sub><2,0 ]]
| |
| − | Es ist ein zusätzlicher Nachweis im Abstand von 1,5(d+h<sub>H</sub>) = 1,5d<sub>H</sub> zu führen, da mit der steileren Stanzkegelneigung (siehe Bild 16) ein Versagen innerhalb der Verstärkung ausgeschlossen werden muss.
| |
| − | <br />
| |
| − | <br />
| |
| − | | |
| − | ==Besonderheiten von Fundamenten==
| |
| − | | |
| − | Bei Bodenplatten und Stützenfundamenten darf in der Fläche <math>A_{crit}</math> die Einwirkung vollständig um den günstig wirkenden Sohldruck abgemindert werden. Durch die Bodenpressung und eine geringere Schubschlankheit fällt der Durchstanzkegel deutlich steiler aus als bei schlanken Deckenplatten. Aufgrund dieser Parameter ist die Lage des maßgeblichen Rundschnitts im Voraus nicht bekannt <ref name="Q9" />.<br />
| |
| − | Die reduzierte Querkraftbeanspruchung ermittelt sich wie folgt:
| |
| − | <br />
| |
| − | <br />
| |
| − | :<math>V_{Ed, red}=V_{Ed}-\Delta V_{Ed}</math>
| |
| − | <br />
| |
| − | Dabei stellt <math>V_{Ed}</math> den resultierenden Sohldruck der kritischen Fläche ohne das Fundamenteigengewicht dar. <br />
| |
| − | | |
| − | Der im Vornherein unbekannte Abstand <math>a_{crit}</math> lässt sich wie folgt ermitteln (NA):
| |
| − | <br />
| |
| − | <br />
| |
| − | *'''gedrungene''' Fundamente <math>\lambda \le 2,0 </math>: interactive Ermittlung des kritischen Rundschnitts
| |
| − | *'''schlanke''' Fundamente <math>\lambda >2,0</math>: konstanter Rundschnitt im Abstand 1,0d.
| |
| − | <br />
| |
| − | mit
| |
| − | <br />
| |
| − | :<math>\lambda=\frac{a_{\lambda}}{d}</math>
| |
| − | <br />
| |
| − | und der Bedingung:
| |
| − | <br />
| |
| − | :<math> a_{crit}\le 2d</math>
| |
| − | <br />
| |
| − | <br />
| |
| − | Bei Fundamenten ohne vorherrschende Normalspannung und somit einem
| |
| − | <br />
| |
| − | :<math>\sigma_{cp} = 0</math>, wird der Nachweis wie folgt geführt:
| |
| − | <br />
| |
| − | :<math>\nu_{Ed}\le\nu_{Rd}=C_{Rd,c}\cdot k\cdot (100\cdot f_{ck})^{1/3}\cdot\frac{2d}{a_{crit}}\ge\nu_{min}\cdot\frac{2d}{a_{crit}}</math>(NA)
| |
| − | <br />
| |
| − | <br />
| |
| − | Da bei Fundamenten ein Einfluss der Schlankheit vorherrscht, wird das geforderte Zuverlässigkeitsniveau nicht erreicht, folglich muss die Gleichung angepasst werden <ref name="Q4" />:
| |
| − | <br />
| |
| − | :<math>C_{Rd,c}=0,15/\gamma_c</math>
| |
| − | [[Datei:Durchstanzen_15.png|300px|thumb|left|Bild 15: Fundament ohne Durchstanzbewehrung ]]
| |
| − | mit <math>\gamma_c=1,5</math>
| |
| − | <br />
| |
| − | Die Einwirkung setzt sich hierbei folgendermaßen zusammen:
| |
| − | <br />
| |
| − | :<math>\nu_{Ed}=\beta\cdot\frac{V_{Ed,red}}{u_{crit\cdot d}}</math><br />
| |
| − | mit
| |
| | <br /> | | <br /> |
| − | :<math>\beta\le 1,10 </math> (NA) | + | * ''Querkrafttragfähigkeit ohne Durchstanzbewehrung:'' außerhalb des durchstanzbewehrtem Bereichs muss die Querkrafttragfähigkeit ohne Durchstanzbewehrung nachgewiesen werden. |
| | <br /> | | <br /> |
| − | *:<math>\beta= 1,10 </math> (NA) für mittige Belastung
| + | ::<math>\nu_ {Ed}\leq\nu_ {Rd,c,out}</math> |
| − | *:<math>\beta= 1+k\cdot\frac{M_{Ed}\cdot u_{crit}}{V_{Ed,red}\cdot W}</math> für aussermittige Belastung
| |
| | <br /> | | <br /> |
| − | Es besteht somit eine Analogie zwischen dem Nachweis der Durchstanztragfähigkeit
| + | Genauere Informationen zu dem Nachweis für Bauteile mit Durchstanzbewehrung: [[Durchstanzen - Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung|Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung]] |
| − | und der Ermittlung der Querkrafttragfähigkeit bei biegebewehrten Stahlbetonbauteilen.
| |
| − | Da durch den rotationssymmetrischen Durchstanzkegel eine höhere Rissverzahnung vorliegt, fällt die Durchstanztragfähigkeit jedoch höher aus <ref name="Q2" />.
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | ====Ermittlung des Abstandes acrit====
| |
| − | [[Datei:Durchstanzen_16.png|300px|thumb|right|Bild 16: Diagramm zur grafischen Herleitung des maßgebenden Rundschnitts bei Einzelfundamenten]] | |
| − | In Abhängigkeit des Abstandes a<sub>crit</sub> kann mit der folgenden Gleichung das maßgebende Minimum ermittelt werden. Somit ergibt sich der relevante kritische Rundschnitt.
| |
| − | <br />
| |
| − | <math>\frac{V_{Rd,c}}{1-\frac{A_{cont}}{A_F}}</math>
| |
| − | <br />
| |
| − | Neben der aufwendigen iterativen Methode zur Ermittlung von acrit bietet das aufgezeigte Diagramm (siehe Bild 15) eine alternative Bestimmungsoption. Dieses stellt die Zusammenhänge der folgenden Eingangsparameter dar <ref name="Q3" />:
| |
| − | <br />
| |
| − | <math>\frac{c}{d} und \frac{l}{c}</math>
| |
| − | <br />
| |
| − | mit | |
| − | *l- Fundamentlänge
| |
| − | *c- Stützenbreite
| |
| − | *d- statische Nutzhöhe
| |
| − | <br />
| |
| − | <br />
| |
| − | <br />
| |
| − | ====Ausmittig belastete Fundamente mit klaffenden Fugen im Rundschnittbereich====
| |
| − | In diesem Fall <math>(e = l/6)</math> sollte die Berechnung über einzelne Sektoren erfolgen. Der abzuziehende Wert für den Sohldruck ergibt sich somit für jeden Sektor separat <ref name="Q8" />.
| |
| | | | |
| − | ===Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung=== | + | ==Beispiel: Berechnung einer Flachdecke mit einer Rundstütze== |
| − | | + | Ein Berechnungsbeispiel findet man auf der Seite: [[Durchstanzen - Flachdecke mit einer Rundstütze (Bsp.)|Flachdecke mit einer Rundstütze (Bsp.)]] |
| − | Ist der Bemessungswert der Einwirkung <math>\nu_{Ed}</math> größer als der Widerstand <math>\nu_{Rd,c}</math> so ist eine Durchstanzbewehrung auszuführen. Bei dem so entstandenen räumlichen Fachwerkmodell werden die Zugstreben von der Durchstanzbewehrung gebildet <ref name="Q4" />. Die möglichen Versagensmechanismen müssen durch mehrere Nachweise geprüft werden. Die Maximaltragfähigkeit <math>\nu_{Rd,max}</math> wird benötigt, um die ausreichende Bewehrungsmenge zu ermitteln. Dieser Wert bezieht sich auf den kritischen Rundschnitt u<sub>1</sub> und sagt aus, ob die Einwirkung <math>\nu_{Ed}</math> durch eine Durchstanzbewehrung aufgenommen werden kann <ref name="Q5" />.
| |
| − | <br />
| |
| − | :<math>\nu_{Ed,u1}=\beta\cdot\frac{V_{Ed}}{u_1\cdot d} \le\nu_{Rd,max}=1,4\cdot\nu_{Rd,c,u1}</math>(NA) | |
| − | Bei der Berechnung von <math>\nu_{Rd,c}</math> darf in diesem Fall keine Betondrucknormalspannung <math>\sigma_{cp}</math> durch eine Vorspannung berücksichtig werden <ref name="Q2" />.
| |
| − | | |
| − | [[Datei:Durchstanzen_17.png|300px|thumb|left|Bild 17: Querkraftdeckung bei Bügeln als Durchstanzbewehrung]] | |
| − | Der Nachweis der Durchstanzbewehrung erfolgt ebenfalls für den kritischen Rundschnitt u<sub>1</sub>. Die so ermittelte Bewehrung wird auf mehrere Rundschnitte verteilt:
| |
| − | :<math>\nu_{Rd,cs}=0,75\cdot\nu_{Rd,c}+1,5\cdot\frac{d}{s_r}\cdot\frac{A_{sw}\cdot f_{ywd,ef\cdot \sin (\alpha)}}{u_1\cdot d}\ge\nu_{Ed,u_1}</math>(NA)
| |
| − | | |
| − | Hieraus ergibt sich die erforderliche Durchstanzbewehrung:
| |
| − | :<math>A_{swJ}=\kappa_{swJ}\cdot\frac{(\nu_{Ed}-0,75\cdot \nu_{Rd,c})\cdot d \cdot u_1}{1,5\cdot\frac{d}{s_r}\cdot f_{ywd,ef}}</math>
| |
| − | mit <math> f_{fwd,ef}=250+0,25\cdot d\le f_{ywd}</math> in N/mm^2 | |
| − | | |
| − | In den ersten zwei Reihen des Rundschnitts ist der Betonstahlquerschnitt <math>Asw</math> aufgrund einer Unterschätzung mit dem Faktor<math>\kappa</math> zu erhöhen<ref name="Q8" />.
| |
| − | *1.Reihe <math>0,3d\le s_{r1}\le 0,5d</math>: <math>\kappa_{sw,1}=2,5</math>
| |
| − | *2.Reihe <math> s_{r2}\le 0,75d</math>: <math>\kappa_{sw,2}=1,4</math>
| |
| − | *bis zur letzten Reihe <math>(s_{ri}\le 0,75d)</math>: <math>\kappa_{sw,i}=1,0</math>
| |
| − | | |
| − | Es wird der größte Wert für s<sub>r</sub> gewählt, jedoch nicht größer als <math>s_{r,max}=0,75d</math>
| |
| − | | |
| − | Es sind mindestens zwei Bewehrungsreihen zu verlegen, welche wie in Bild 16 anzulegen sind. Die letzte Bewehrungsreihe ist im Abstand <math>\le 1,5d </math>vom äußeren Rundschnitt <math>u_{out}</math> anzulegen (siehe Bild 17).
| |
| − | [[Datei:Durchstanzen_18.png|200px|thumb|right|Äußerer Rundschnitt]]
| |
| − | Dieser ergibt sich wie folgt:
| |
| − | :<math>u_{out}=\beta\cdot\frac{V_{Ed}}{\nu_{Rd,c}\cdot d}</math>
| |
| − | | |
| − | | |
| − | Somit muss nachgewiesen werden, dass im kritischen Rundschnitt u<sub>out</sub> keine Durchstanzbewehrung mehr erforderlich ist:
| |
| − | <math>\nu_{Ed,out}=\beta\cdot\frac{V_{Ed}}{\nu_{out}\cdot d}\le \nu_{Rd,c}</math>
| |
| − | | |
| − | Zur Bestimmung des Betontraganteils <math>\nu_{Rd,c} wird der Faktor <math>C_{Rd,c}=0,15/ \gamma_c</math> angesetzt.
| |
| − | Dieser Wert stellt hier die Tragfähigkeit einer liniengelagerten Platte ohne Querkraftbewehrung unter Berücksichtigung des Längsbewehrungsgrads<math\rho_l</math> im äußeren Rundschnitt dar <ref name="Q4" />.
| |
| − | | |
| − | ====Besonderheiten von Fundamenten und Bodenplatten====
| |
| − | | |
| − | Bei Fundamenten ist die reduzierte einwirkende Querkraft <math>V_{Ed,red}</math> von den ersten zwei Bewehrungsreihen voll aufzunehmen, dabei ist der Betontraganteil nicht in Abzug zu bringen. Die erforderliche Bewehrung ist gleichmäßig auf die ersten beiden Reihen zu verteilen <ref name="Q1" />.
| |
| − | *1. Reihe im Abstand <math>s_0=0,3d</math> und
| |
| − | *2. Reihe im Abstand <math>s_0+s_1=0,8d</math>
| |
| − | | |
| − | Die Maximaltragfähigkeit des Fundaments setzt sich folgendermaßen zusammen:
| |
| − | :<math>\nu_{Rd,max}=1,4\cdot\nu_{Rd,c,u1}</math>
| |
| − | | |
| − | Bei Fundamenten ist u<sub>1</sub> gegebenenfalls durch den interativ ermittelten Wert von u im Abstand acrit zu ersetzen. Hier darf bei der Ermittlung von <math>\nu_{Rd,c}</math> keine Betondruckspannung<math>\sigma_{cp}</math> durch eine Vorspannung berücksichtigt werden <ref name="Q1" />. Wird der Maximalwert überschritten, so müssen Maßnahmen zur Steigerung des Querkraftwiderstands ergriffen werden.
| |
| − | Hierzu gehören<ref name="Q3" />:
| |
| − | *Erhöhung der Betongüte
| |
| − | *Vergrößerung der Fundamentenhöhe
| |
| − | *oder Erhöhung des Bewehrungsgrades
| |
| − | | |
| − | Folgende Nachweise sind zu führen <ref name="Q4" />:
| |
| − | *für '''Bügelbewehrung''':
| |
| − | :<math>\beta\cdot V_{Ed,red}\le V_{Rd,s}=A_{sw, 1+2}\cdot f_{ywd,ef}</math>
| |
| − | Umgestellt zur Ermittlung der Bewehrungsmenge:
| |
| − | :<math>A_{sw, 1+2}=\frac{\beta\cdot V_{Ed,red}}{f_{ywd,ef}}</math>
| |
| − | *für '''Schrägbewehrung''':
| |
| − | :<math>\beta\cdot V_{Ed,red}\le V_{Rd,s}=1,3\cdot A_{sw, 1+2}\cdot f_{ywd,ef}\cdot \sin(\alpha)</math>
| |
| − | | |
| − | Weitere eventuell erforderliche Bewehrungsreihen werden mit 33 % von <math>A_{sw,1+2}</math> versehen.
| |
| − | :<math> 0,33\cdot A_{sw,1+2}</math>
| |
| − | Hierbei darf innerhalb der betrachteten Bewehrungsreihe die Bodenpressung der Fundamentfläche in Abzug gebracht werden <ref name="Q8" />.
| |
| − | | |
| − | ===Mindestmomente für Platten-Stützen-Verbindungen===
| |
| − | [[Datei:Durchstanzen_19.png|500px|thumb|right|Bild 19: Momentenbeiwert und Verteilungsbreiten der Mindestmomente mEd]]
| |
| − | [[Datei:Durchstanzen_20.png|300px|thumb|right|Bild 20: Ansatz der Mindestmomente]]
| |
| − | Die Sicherheit gegen Durchstanzen bei nicht berücksichtigten Exzentrizitäten wird durch die Berechnung der Mindestmomente <math>mEd,x</math> und <math>mEd,y</math> gewährleistet. Diese sollen eine Begrenzung der Schubrissweiten und die Erhaltung des räumlichen Tragmodells sicherstellen. Bei Erhalt von größeren Werten durch die Schnittgrößenermittlung sind diese maßgebend <ref name="Q4" />. Es dürfen nur die Bewahrungsstäbe berücksichtigt werden, welche außerhalb des kritischen Rundschnitts verankert sind.
| |
| − | Die Mindestmomente ergeben sich wie folgt:
| |
| − | *<math>mEd,x=\eta_x\cdot V_{Ed}</math>
| |
| − | *<math>mEd,y=\eta_y\cdot V_{Ed}</math>
| |
| − | | |
| − | | |
| − | | |
| − | Die Anordnung der Bewehrung erfolg nach Bild 20.
| |
| − | | |
| − | ===Mindestbewehrung und Konstruktionsregeln===
| |
| − | [[Datei:Durchstanzen_21.png|300px|thumb|left|Bild 21: Schrägstäbe als Durchstanzbewehrung]]
| |
| − | Ist in einer Platte eine Durchstanzbewehrung vorzusehen, so muss die Platte eine Mindestdicke von 20 cm aufweisen <ref name="Q8" />. Die vorgesehene Durchstanzbewehrung ist bei Deckenplatten in der oberen, bei Fundamenten in der unteren Lage anzuordnen, da diese die Zugseiten darstellen. Bei der Ermittlung von Durchstanzbewehrung, darf die Grundbewehrung angerechnet werden. Existieren nebenliegende Durchbrüche, so dürfen diese nicht größer als 1/3 der Stützenbreite, beziehungsweise des Durchmessers der Stütze ausfallen <ref name="Q7" />. Der Stabdurchmesser der Durchstanzbewehrung ist an die mittlere Nutzhöhe der Platte anzupassen<ref name="Q5" />:
| |
| − | *bei '''Bügeln''':
| |
| − | :∅<math>\le 0,05d</math>
| |
| − | * bei '''Schrägaufbiegung''':
| |
| − | :∅<math>\le 0,08d</math>
| |
| − | '''Maximaler''' tangentialer '''Abstand''' der Bügelschenkel
| |
| − | *innerhalb des kritischen Rundschnitts s<sub>t</sub>= 1,5d
| |
| − | *außerhalb des kritischen Rundschnitts s<sub>t</sub>=2,0d
| |
| − | | |
| − | Als '''Mindestbewehrung''' gilt (je Bügelschenkel)(NA):
| |
| − | :<math>A_{sw,min}=A_s\cdot \sin(\alpha)=\frac{0,08\cdot \sqrt{f_{ck}}\cdot s_r \cdot s_t}{f_{yk}\cdot 1,5}</math>
| |
| − | | |
| − | Schrägstäbe sind in einem Winkel von <math>45 < \alpha < 60</math> zur Bauteilachse auszuführen.
| |
| − | | |
| − | Dabei ist ihre Aufbiegungen im Bereich <math>\le 1,5d </math> um die Stütze anzulegen. Bei aufgebogenen Schrägstäben ist eine Bewehrungsreihe ausreichend, welche mit einem s<sub>r</sub>= 0,67d angenommen werde kann <ref name="Q9" />.
| |
| − | Bei der Berechnung des Bauteiltragwiderstands ist das Verhältnis d/s<sub>r</sub>= 0,53 zu beachten.
| |
| − | Des Weiteren kann die Bewehrung bis f<sub>ywd,ef</sub> = f<sub>ywd</sub> ausgereizt werden, da Schrägstäbe selbst bei dünnen Platten die Streckgrenze erreichen <ref name="Q1" />. Darüber hinaus müssen mindestens 50 % der Längsbewehrung in radialer oder tangentialer Richtung von der Durchstanzbewehrung umschlossen werden.
| |
| − | :Querkraftzulagen sind als Durchstanzbewehrung unzulässig <ref name="Q3" />.
| |
| | | | |
| | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] |
| Zeile 523: |
Zeile 118: |
| | <references /> | | <references /> |
| | | | |
| − | {{Seiteninfo(mb) | + | |
| − | |Quality-flag = [[File:quality-flag-white.gif|right|70px]] | + | {{Seiteninfo |
| − | |Status = in Bearbeitung| | + | |Quality-flag = [[File:quality-flag-green.gif|right|70px]] |
| − | |Modul-Version = 2015.0240}} | + | |Status = Seite geprüft, inhaltlich OK|}} |