Verankerungslänge: Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) K |
|||
| (36 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Die Verankerungslänge bezeichnet | + | [[Datei:Verankerungslänge 8.JPG|300px|right]] |
| + | Die Verankerungslänge bezeichnet den Abschnitt am Ende eines Bewehrungsstabes, in dem die am Beginn der Verankerungslänge wirkende Zug- oder Druckkraft vollständig über Verbund in den Beton eingeleitet wird. Ziel der Bemessung der Verankerungslänge ist, dass keine Überschreitung der Trägfähigkeit der Betonkonsole und der Zugfestigkeit des Betons in Querrichtung stattfindet. | ||
| − | |||
| − | + | = Allgemeines= | |
| − | + | Endet ein Stab sind die Zugkräfte am Stabende im beton zu verankern. Die Verankerung kann über Verbund oder mechanische Verbindungsmittel z.B. Ankerplatten erfolgen. Die Verankerung über Verbund ist die einfachste und wirtschaftlichste Methode, Verankerungen mit mechanischen Verbindungsmitteln sind nur in Sonderfällen sinnvoll und sollen nicht Thema dieser Seite sein. Die Sicherstellung einer ausreichenden Verankerungslänge gehört zu den notwendigen Nachweisen eines Bauteils und gliedert sich in den Arbeitsabschnitt "konstruktive Durchbildung der Bewehrung" ein. | |
| − | + | == Verbund zwischen Beton und Stahl == | |
| − | - | + | [[Datei:Verankerungslänge 1.JPG|300px|thumb|Kraftübertragung zwischen Beton und Stahl|right]] |
| − | + | Die Übertragung von Kräften zwischen Beton und Bewehrungsstahl erfolgt über den Haft-, Reib- und Formverbund, den größten Anteil an der Kraftübertragung hat hierbei der Formverbund. Da bei der Berechnung auch nur der Formverbund berücksichtigt wird, wird auf den Haft- und Reibverbund im folgenden nicht näher eingegangen. | |
| − | - | ||
| − | |||
| − | - | ||
| − | + | Bei dem genormten Betonstahl wird der Formverbund durch eine Oberflächenprofilierung in Form von Ripppen sichergestellt. Haupteinflussfaktoren auf den Formverbund sind die Form und Neigung der Rippen, die Rippenhöhe und der Rippenabstand. Bei geringen Relativverschiebungen zwischen Bewehrung und Beton stützen sich die Rippen auf dem Beton ab, eine Art Betonkonsole entsteht. | |
| − | = | + | Aufgrund der Anordnung und Form der Rippen findet die Kraftübertragung in Form von ringförmigen schrägen Betondruckstreben statt. Aus Gleichgewichtsgründen bilden sich außerdem Zugspannungsringe senkrecht zur Stabachse.<ref>Vgl. Avak, Ralf: Stahlbetonbau in Beispielen. DIN 1045. Teil 1, Köln 2007 (5. Auflage), S. 53.</ref> Damit sich diese Zugspannungen aufgenommen werden können, muss eine ausreichende Betondeckung vorhanden sein. Eine zu geringe Betondeckung oder ein zu geringer Stababstand können Längsrisse parallel zur Stabachse zur Folge haben und damit die Verbundwirkung beeinträchtigen.<ref>Vgl. Wommelsdorff, Otto; Albert, Andrej; Fischer, Jürgen: Stahlbetonbau. Bemessung und Konstruktion. Teil 1, Köln 2017 (11. Auflage), S. 87.</ref>. Die Tragfähigkeit der Verankerung ist maßgeblich davon abhängig ob die Rissbildung infolge Querzugspannungen im Verankerungsbereich verhindert wird oder nicht <ref Name = "Q2">Zilch,K., Zehetmaier,G., Bemessung im konstruktiven Betonbau, 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006</ref>. |
| − | + | Wegen der Querzugspannungen ist im Verankerungsbereich grundsätzlich Querbewehrung anzuordnen. Die in der Norm geforderte Querbewehrung ist in der Regel allerdings bereits durch die Mindestquerbewehrung bei Platten oder die Mindestquerkraftbewehrung bei Balken vorhanden, | |
| − | + | == Verbundfestigkeit == | |
| − | |||
| − | Die | + | Die Größe der aufnehmbaren Verbundspannung wird als Verbundfestigkeit bezeichnet. Sie ist abhängig von der Oberflächenbeschaffenheit des Bewehrungsstabs und der Betonzugfestigkeit. Die Berechnung der Verbundfestigkeit kann mit folgender Gleichung erfolgen, die Gleichung ist nur für Betonstahl nach DIN EN 10080 <ref Name = "Q1">DIN EN 10080, Stahl für die Bewehrung von Beton - Schweißgeeigneter Betonstahl - Allgemeines, Beuth-Verlag, 2005</ref> anwendbar, eine Anwendung für Stäbe mit anderen Eigenschaften z.B. glatte Bewehrungsstäbe ist nicht zulässig. |
| − | + | :<math>f_{bd} = 2,25 \cdot \eta_1 \cdot \eta_2 \cdot \frac{f_{ctk;0,05}}{\gamma_c}</math> | |
| − | <math>f_{bd} = 2,25 \cdot \eta_1 \cdot \eta_2 \cdot \frac{f_{ctk;0,05}}{\gamma_c}</math> | ||
| − | |||
| − | + | wobei: | |
| − | {| | + | :{| |
|- | |- | ||
| <math>\eta_1</math> || ein Beiwert für die Verbundbedingungen | | <math>\eta_1</math> || ein Beiwert für die Verbundbedingungen | ||
| Zeile 41: | Zeile 35: | ||
| <math>f_{ctk;0,05}</math> || der 5 %-Quantil-Wert der charakteristischen Betonzugfestigkeit | | <math>f_{ctk;0,05}</math> || der 5 %-Quantil-Wert der charakteristischen Betonzugfestigkeit | ||
|- | |- | ||
| − | | <math>\gamma_c</math> || der | + | | <math>\gamma_c</math> || der Teilsicherheitsbeiwert für die Betonfestigkeit |
|} | |} | ||
<br /> | <br /> | ||
| + | [[Datei:Verankerungslänge 11.jpg|300px|thumb|Festlegun der Bereiche mit guten und mäßigen Verbundbedingungen nach <ref Name = "Q5"></ref>|right]] | ||
| + | |||
| + | Mit dem Beiwert <math>\eta_1</math> wird die Lage der Bewehrung im Bauteil berücksichtigt. Abhängig von der Lage wird zwischen guten und mäßigen Verbundbedingungen unterschieden. Mäßige Verbundbedigungen entstehen, wenn während des Verdichtens Luft und Wasser im Beton nach oben transportiert werden und sich unter oben liegenden Stäben ansammeln. Nach der Aushärtung des Betons bilden sich hier Poren oder Ablösungen, so dass der Verbund zwischen Beton und Stahl in diesem Bereich beeinträchtigt ist. | ||
| − | + | Als Stäbe mit guten Verbundbedigungen gelten Stäbe, welche sich während des Betonierens im unteren Bereich (vgl. Grafik) des Bauteils befinden sowie Stäbe mit einer Neigung >45° bezogen auf die Betonierrichtung. Nähere Informationen zu den Verbundbedingungen können der Grafik entnommen werden. Die Werte für <math>\eta_1</math> werden im EC2 <ref Name = "Q5">DIN EN 1992-1-1, Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2011</ref> folgendermaßen definiert: | |
| − | {| | + | :{| |
|- | |- | ||
| <math>\eta_1 = 1,0</math> || für gute Verbundbedingungen | | <math>\eta_1 = 1,0</math> || für gute Verbundbedingungen | ||
|- | |- | ||
| <math>\eta_1 = 0,7</math> || für mäßige Verbundbedingungen | | <math>\eta_1 = 0,7</math> || für mäßige Verbundbedingungen | ||
| + | |} | ||
| + | |||
| + | Der Beiwert <math>\eta_2</math> berücksichtigt sehr große Stabdurchmesser. Ab einem Grenzwert von Ø<sub>s</sub> = 32 mm nimmt die Verbundfestigkeit bei sonst gleich bleibenden Bedingungen aufgrund der erhöhten Spaltrissgefahr ab. Der Beiwert wird berechnet mit | ||
| + | |||
| + | :{| | ||
| + | |- | ||
| + | | <math>\eta_2 = 1,0</math> || für Ø<sub>s</sub> ≤ 32 mm | ||
| + | |- | ||
| + | | <math>\eta_2 = (132 - \varnothing_s)/100</math> || für Ø<sub>s</sub> > 32 mm | ||
|} | |} | ||
<br /> | <br /> | ||
| − | + | Die Zugfestigkeit <math>f_{ctk;0,05}</math> ist auf die Betondruckfestigkeit <math>f_{ck}</math> zurückführbar. Am einfachsten ist es daher, Tabellen zu benutzen, aus denen die Zugfestigkeit <math>f_{ctk;0,05}</math> bzw. die Verbundfestigkeit <math>f_{bd}</math> in Abhängigkeit von <math>f_{ck}</math> ablesbar sind.<ref Name = "Schneider">Albert, Andrej (Hg.): Schneider Bautabellen für Ingenieure, Köln 2020 (24. Auflage), S. 5.108.</ref>. Da der Beton mit zunehmender Festigkeit spröder wird, wird die Betonzugfestigkeit für die Ermittlung der Verbundfestigkeit auf den Wert für C60/75 begrenzt. | |
| − | + | <br /> | |
| − | <br /> | + | ==Einflussfaktoren auf die Verankerungslänge== |
| − | <math> | + | Im folgenden wird auf Faktoren eingegangen, welche die Verankerungslänge beeinflussen: |
| + | <br> | ||
| + | <li>'''Stabdurchmesser:''' | ||
| + | Mit abnehmendem Stabdurchmesser nimmt die Mantelfläche des Stabs im Verhältnis zur Querschnittsfläche zu. Hierdurch steht eine größere Fläche für die gleiche zu übertragende Zugkraft zur Verfügung, was sich positiv auf die Verankerungslänge auswirkt. Aus Sicht der Verankerungslänge ist es daher sinnvoll mehrere dünnere Stäbe zu verwenden als wenige große. | ||
| + | </ul> | ||
| + | <br> | ||
| + | <li>'''Stahlspannung:''' | ||
| + | Der Einfluss der Stahlspannung ist ähnlich zu dem des Stabdurchmessers. Mit abnehmender Stahlspannung müssen bei gleicher zur Verfügung stehenden Mantelfläche weniger Zugkräfte in den Beton übertragen werden. Steuern lässt sich die Stahlspannung bei vorgegebener Belastung durch die gewählte Bewehrungsquerschnittsfläche. Mit zunehmender Bewehrungsquerschnittsfläche nimmt die Stahlspannung ab. Eine Vergrößerung der Bewehrungsquerschnittsfläche muss für die Verringerung der Stahlspannung nicht auf der gesamten Stablänge vergrößert werden, sie kann auch nur im Bereich der Verankerungslänge durch die Anordnung einer Zulagebewehrung vergrößert werden. | ||
| + | </ul> | ||
| + | <br> | ||
| + | <li>'''Betonfestigkeitsklasse:''' | ||
| + | Die Betonfestigkeitsklasse hat über die von ihr abhängige Betonzugfestigkeit Einfluss auf die Verankerungslänge, außerdem steigt durch die steigende Druckfestigkeit auch die Tragfähigkeit der Betonkonsole. Mit zunehmender Zugfestigkeit nimmt die erforderliche Verankerungslänge ab. | ||
| + | </ul> | ||
| + | <br> | ||
| + | <li>'''Querdruck:''' | ||
| + | Querdruck hat einen positiven Einfluss auf die Verankerungslänge, da hierdurch der Verbund zwischen Beton und Bewehrung erhöht wird. Außerdem können unter Querdruck größere Querzugspannungen durch den Beton aufgenommen werden. Querdruck ist üblicherweise im Auflagerbereich vorhanden. | ||
| + | </ul> | ||
| + | <br> | ||
| + | <li>'''Querzug:''' | ||
| + | Querzug hat den gegenteiligen Effekt wie Querdruck. Die Verankerungslänge erhöht sich, da sich der Verbund zwischen Bewehrung und Beton verschlechtert und weniger Querzugspannugen infolge der Verankerung aufgenommen werden können. | ||
| + | </ul> | ||
| + | <br> | ||
| + | <li>'''Lage des Stabs im Bauteil:''' | ||
| + | Auf den Einfluss der Lage des Stabs im Bauteil wurde bereits früher auf dieser Seite genauer eingegangen. In Bereichen mit mäßigen Verbundbedingungen sind kleinere Verankerungslängen erforderlich als in Bereichen mit mäßigen. | ||
| + | </ul> | ||
| + | <br> | ||
| + | == Kleine Herleitung der Verankerungslänge == | ||
| + | |||
| + | Im Zuge der Bemessung eines Bauteils wird die nötige Bewehrung bereichsweise für die jeweils maximalen auftretenden Schnittgrößen bestimmt. In der anschließenden konstruktiven Durchbildung wird dann zum Beispiel im Rahmen der [[Zugkraftdeckung]] die ermittelte Zugbewehrung dem tatsächlichen Momentenverlauf angepasst und abgestuft. Die so entstehenden Stabenden können nicht direkt an dem Punkt, an dem sie rechnerisch nicht mehr benötigt werden, enden. Vielmehr muss die an diesem Punkt noch im Stab vorhandene Zugkraft im Beton „verankert“ werden, weshalb dieser zusätzliche Stababschnitt als Verankerungslänge <math>l_b</math> bezeichnet wird. | ||
| + | |||
| + | [[Datei:Verankerungslänge 9.JPG|300px|thumb|Verlauf der Verbundspannungen|right]] | ||
| + | <!--Zur Ermittlung der Verankerungslänge wird die zwischen Stahl und Beton wirkende Verbundspannung vereinfachend als konstant angenommen, eine Gegenüberstellung mit dem tatsächlichen Verlauf ist im Bild rechts dargestellt. Der Unterschied zwischen Gebrauchszustand (Grenzzustand der Gebrauchstauglichkeit) und Bruchzustand (Grenzzustand der Tragfähigkeit) erklärt sich hierbei über das Tragverhalten des Betons.//--> | ||
| + | Bei niedriger Beanspruchung ist der Beton an der Stelle der Lasteinleitung ungeschädigt und die Verbundspannung dementsprechend hoch. Erhöht sich die Belastung, so wird der Beton zunächst an der Lasteinleitungsstelle geschädigt (plastisch deformiert), wodurch sich die Verbundspannung in die vorher weniger beanspruchten Bereiche umlagert.<ref>Vgl. König, Gert; Tue, Nguyen Viet: Grundlagen des Stahlbetonbaus. Einführung in die Bemessung nach DIN 1045-1, Wiesbaden 2003 (2. Auflage), S. 416.</ref> In der Berechnung wird dieses komplexe Umlagerungsverhalten nicht berücksichtigt und die Verbundspannung wird als über die Verankerungslänge und den Stabumfang konstant angesetzt. | ||
| + | |||
| + | [[Datei:Verankerungslänge 8.JPG|300px|thumb|Grundlage der Verankerungslänge|right]] | ||
| + | In der dargestellten Skizze muss die Zugkraft <math>F_{sd}</math> vom Stab in den Beton mittels Verbundspannung übertragen werden. Aus Gleichgewichtsgründen gilt nun, dass die zu verankernde Zugkraft <math>F_{sd}</math> kleinergleich der Verbundfestigkeit <math>f_{bd}</math> multipliziert mit der Mantelfläche des Stabes <math>l_b \cdot u</math> sein muss, also: | ||
| + | |||
| + | :<math>F_{sd} = f_{bd} \cdot l_b \cdot u</math> | ||
| − | + | Der Umfang des Bewehrungsstabes wird berechnet mit | |
| − | + | :<math>u = \pi \cdot \varnothing_s</math> | |
| − | + | Die Gleichung für <math>F_{sd}</math> umgestellt nach der benötigten ("required") Verankerungslänge ergibt | |
| − | = | + | :<math>l_{b,rqd} = \frac{F_{sd}}{\pi \cdot \varnothing_s \cdot f_{bd}}</math> |
| − | = | + | Die bisher unbekannte Zugkraft <math>F_{sd}</math> ist das Produkt von Stahlspannung <math>\sigma_{sd}</math> und Bewehrungsfläche <math>A_s</math>. Die Bewehrungsfläche eines Stabs ist <math>A_s = \frac{\pi}{4} \cdot \varnothing_s^2</math>. Eingesetzt in die Gleichung der Verankerungslänge ergibt sich |
| − | + | :<math>l_{b,rqd} = \frac{\frac{\pi}{4} \cdot \varnothing_s^2 \cdot \sigma_{sd}}{\pi \cdot \varnothing_s \cdot f_{bd}} = \frac{\varnothing_s}{4} \cdot \frac{\sigma_{sd}}{f_{bd}}</math> | |
| + | Diese Gleichung wird auch als Grundwert der Verankerungslänge bezeichnet. Wenn im Verankerungsbereich nicht die volle Stahlspannung ausgenutzt wird, darf die Verankerungslänge proportional zum Verhältnis von vorhandener zu erforderlicher Bewehrung reduziert werden. Diese Abminderung wird i.d.R. im Rahmen der Spannungsermittlung berücksichtigt: | ||
| − | + | :<math>\sigma_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}}</math> | |
| − | <math> | ||
| − | + | == Formen und Beiwerte der Verankerungslänge == | |
| − | + | === Bemessungswert der Verankerungslänge === | |
[[Datei:Verankerungslänge 2.png|200px|thumb|right]] | [[Datei:Verankerungslänge 2.png|200px|thumb|right]] | ||
| − | Der Bemessungswert der Verankerungslänge <math>l_{bd}</math> misst die Länge vom Beginn der Verankerungslänge bis zum Stabende. Die Formel hierfür ist | + | Der Bemessungswert der Verankerungslänge <math>l_{bd}</math> wird aus dem Grundwert der Verankerungslänge abgeleitet und misst die Länge vom Beginn der Verankerungslänge bis zum Stabende. Die Formel hierfür ist |
<br /> | <br /> | ||
| Zeile 90: | Zeile 133: | ||
<br /> | <br /> | ||
| − | + | === Ersatzverankerungslänge === | |
[[Datei:Verankerungslänge 3.png|200px|thumb|right]] | [[Datei:Verankerungslänge 3.png|200px|thumb|right]] | ||
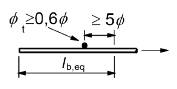
| − | Alternativ zur Bestimmung der tatsächlichen, gegebenenfalls gebogenen Verankerungslänge <math>l_{bd}</math> kann vereinfacht die gerade Stablänge <math>l_{b,eq}</math> ermittelt werden. Die Formel hierfür lautet | + | Alternativ zur Bestimmung der tatsächlichen, gegebenenfalls gebogenen Verankerungslänge <math>l_{bd}</math> kann vereinfacht die gerade Stablänge <math>l_{b,eq}</math> ermittelt werden; diese misst die Länge vom Ende der Biegeform bis zum Beginn der Verankerungslänge. Die Formel hierfür lautet |
<br /> | <br /> | ||
| Zeile 98: | Zeile 141: | ||
<br /> | <br /> | ||
| − | Die Ermittlung von <math>l_{b,eq}</math> ist | + | Die Ermittlung von <math>l_{b,eq}</math> ist der Regelfall bei der Ermittlung der Verankerungslänge. |
<br /> | <br /> | ||
| − | + | === Beiwerte der Verankerungslänge === | |
Bei der Ermittlung des Bemessungswerts der Verankerungslänge <math>l_{bd}</math> oder der Ersatzverankerungslänge <math>l_{b,eq}</math> aus dem Grundwert der Verankerungslänge <math>l_{b,rqd}</math> kommen einige Beiwerte zum Einsatz. Diese sind wie folgt: | Bei der Ermittlung des Bemessungswerts der Verankerungslänge <math>l_{bd}</math> oder der Ersatzverankerungslänge <math>l_{b,eq}</math> aus dem Grundwert der Verankerungslänge <math>l_{b,rqd}</math> kommen einige Beiwerte zum Einsatz. Diese sind wie folgt: | ||
| Zeile 128: | Zeile 171: | ||
<math>{\alpha_1}</math> - <u>Formgebung</u>: | <math>{\alpha_1}</math> - <u>Formgebung</u>: | ||
| − | + | Die Verankerungslänge kann durch abgebogene Stabenden z.B. Haken, Winkelhaken oder Schlaufen verkürzt werden, da Teile der Zugkraft durch Umlenk-bzw. Kontaktpressung aufgenommen werden <ref Name = "Q2"></ref>. Voraussetzung hierfür ist, dass die entstehenden Spaltzugkräfte infolge der Umlenkung durch den Beton aufgenommen werden können. Ist dies nicht der Fall kann die positive Wirkung von abgebognen Stabenden dennoch angesetzt werden, wenn eine enge Verbügelung im Bereich der Abbiegung angeordnet wird. | |
Bei der Verwendung von Schlaufen besteht zusätzlich die Möglichkeit, unter Einhalten von <math>c_d > 3 \O_s</math> und eines Biegerollendurchmessers <math>D \geq 15 \O_s</math>, den Beiwert auf <math>{\alpha}_1 = 0,5</math> zu reduzieren. | Bei der Verwendung von Schlaufen besteht zusätzlich die Möglichkeit, unter Einhalten von <math>c_d > 3 \O_s</math> und eines Biegerollendurchmessers <math>D \geq 15 \O_s</math>, den Beiwert auf <math>{\alpha}_1 = 0,5</math> zu reduzieren. | ||
| − | + | Die Verankerung von Druckstäben mit abgebogenem Stabende ist grundsätzlich unzulässig, da die entstehenden Kräfte zu einer Absprengung der Betondeckung führen können. Auch Stäbe mit einem Durchmesser >32mm dürfen nur mit geradem Stabende verankert werden. | |
[[Datei:Verankerungslänge 5.png|300px|Abstand cd für Balken und Platten|thumb|right]] | [[Datei:Verankerungslänge 5.png|300px|Abstand cd für Balken und Platten|thumb|right]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<math>{\alpha_2}</math> - <u>Mindestbetondeckung</u>: | <math>{\alpha_2}</math> - <u>Mindestbetondeckung</u>: | ||
| Zeile 148: | Zeile 186: | ||
<math>{\alpha}_2 = max\left\{ {\begin{matrix} 1 - \frac{0,15 \cdot (c_d - \O_s)}{\O_s} \\ 0,7 \end{matrix}} \right\} \leq 1,0</math> | <math>{\alpha}_2 = max\left\{ {\begin{matrix} 1 - \frac{0,15 \cdot (c_d - \O_s)}{\O_s} \\ 0,7 \end{matrix}} \right\} \leq 1,0</math> | ||
| − | In Deutschland ist dieser Beiwert aus der Formel zur Ermittlung des Bemessungswerts der Verankerungslänge gestrichen. | + | In Deutschland ist dieser Beiwert aus der Formel zur Ermittlung des Bemessungswerts der Verankerungslänge gestrichen. Grund hierfür ist, dass eine größere Betondeckung zwar die Entstehung von Spaltrissen verhindert, die Sicherheit gegen Herausziehen der Bewehrung aber nicht erhöht. Würde die Verankerungslänge mit diesem Beiwert reduziert, würde der Versagensfall Herausziehen nicht ausreichend berücksichtigt bzw. unterschätzt. Die Berücksichtigung dieses Bwiwerts liegt somit auf der unsicheren Seite. |
<br /> | <br /> | ||
| Zeile 186: | Zeile 224: | ||
[[Datei:Verankerungslänge 7.png|300px|Angeschweißter Querstab|thumb|right]] | [[Datei:Verankerungslänge 7.png|300px|Angeschweißter Querstab|thumb|right]] | ||
| − | + | Die Anwesenheit angeschweißter Querstäbe hat aus dem gleichen Grund wie die Stabform einen positiven Effekt auf die Verankerungslänge, da Teile der Zugkraft durch Umlenk-bzw. Kontaktpressung aufgenommen werden<ref Name = "Q2"></ref>. Werden die angegebenen Bedingungen eingehalten, so gilt sowohl für Zug- als auch für Druckstäbe <math>\alpha_4 = 0,7</math>. | |
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| − | |||
<math>{\alpha_5}</math> - <u>Querdruck</u>: | <math>{\alpha_5}</math> - <u>Querdruck</u>: | ||
| Zeile 214: | Zeile 248: | ||
<br /> | <br /> | ||
| − | + | === Mindestverankerungslänge === | |
| + | |||
| + | Die Mindestverankerungslänge soll sicherstellen, dass trotz Verlegeungenauigkeiten eine ausreichende Verankerungslänge vorhanden ist. Außerdem soll das Maß, um das die Verankerungslänge durch Zulagbewehrung reduziert werden kann, begrenzt werden. | ||
Für Zugstäbe ist die Mindestverankerungslänge definiert als | Für Zugstäbe ist die Mindestverankerungslänge definiert als | ||
| Zeile 236: | Zeile 272: | ||
<br /> | <br /> | ||
| − | = | + | = Nachweis-Situationen der Verankerungslänge = |
| − | |||
| − | + | Die verschiedenen Situationen der Verankerungslänge unterscheiden sich vor allem in der Ermittlung der erforderlichen Bewehrungsmenge an der jeweiligen Stelle. Darüber hinaus gelten gegebenenfalls besondere Regeln für die Bestimmung von <math>l_{bd}</math>, <math>l_{b,eq}</math> und <math>l_{b,min}</math>. | |
| − | + | == Verankerung am Endauflager == | |
| − | + | Zunächst muss die Randzugkraft, d.h. die Zugkraft am Endauflager bestimmt werden: | |
| + | ::<math>F_\mathrm{Ed} =V_\mathrm{Ed}\cdot\cfrac{a_\mathrm{l}}{z}+N_\mathrm{Ed}\ge\cfrac{V_\mathrm{Ed}}{2}</math> | ||
| + | :::{| | ||
| + | | V<sub>Ed</sub>... || Bemessungswert der einwirkenden Querkraft | ||
| + | |- | ||
| + | | a<sub>l</sub>... || [[Versatzmaß]] aus Zugkraftdeckung | ||
| + | |- | ||
| + | | z... || Hebelarm der inneren Kräfte | ||
| + | |- | ||
| + | | N<sub>Ed</sub>... || Bemessungswert der einwirkenden Normalkraft | ||
| + | |} | ||
| + | Anschließend kann die erforderliche Bewehrungsmenge und daraus die Stahlspannung ermittelt werden. | ||
| + | ::<math>A_\mathrm{s,erf} =\cfrac{F_\mathrm{Ed}}{f_\mathrm{yd}}</math> | ||
| + | :::{| | ||
| + | | f<sub>yd</sub>... || Bemessungswert der Stahlstreckgrenze | ||
| + | |} | ||
| + | ::<math>\sigma_\mathrm{sd} =\cfrac{A_\mathrm{s,erf}}{A_\mathrm{s,vorh}}\cdot f_\mathrm{yd}</math> | ||
| + | :::{| | ||
| + | | A<sub>s,vorh</sub>... || Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe | ||
| + | |} | ||
| + | Mithilfe der zuvor bestimmten Stahlspannung lässt sich die Verankerungslänge über die dafür allgemeingültigen Formeln bestimmen. | ||
| + | [[Verankerung am Endauflager (Bsp.)|Berechnungsbeispiel zur Verankerung am Endauflager]] | ||
| − | + | == Verankerung am Zwischenauflager == | |
| − | |||
| − | + | Die am Zwischenauflager endende Feldbewehrung liegt i.d.R im Druckbereich. Deshalb ist sie in vielen Fällen rechnerisch nicht nötig, es gilt <math>A_{s,erf} = 0</math>, gleiches gilt damit auch für <math>{\sigma}_{sd}</math> und <math>l_{b,rqd}</math>. Aus diesem Grund ist am Zwischenauflager <math>l_{b,min}</math> maßgebend. Die Verankerungslänge am Zwischenauflager beginnt an der Auflagerkante. | |
| − | + | Da es sich hier meistens um Druckstäbe handelt sind abgebogenen Stabenden nicht zulässig. | |
| − | + | [[Verankerung am Zwischenauflager (Bsp.)|Berechnungsbeispiel zur Verankerung am Zwischenauflager]] | |
| + | == Verankerung außerhalb von Auflagern == | ||
| − | [[ | + | Abseits der Auflager eines Balkens enden Bewehrungsstäbe im Kontext der [[Zugkraftdeckung]]. Ab der Stelle an der sie nicht mehr erforderlich sind, sind Stäbe zu verankern. Hier sind erforderliche und vorhandene Bewehrung unmittelbar bekannt. |
| − | < | + | Ermittlung der Stahlspannung am rechnerischen Endpunkt E: |
| + | ::<math>\sigma_\mathrm{sd} =\cfrac{A_\mathrm{s,erf}}{A_\mathrm{s,vorh}}\cdot f_\mathrm{yd}</math> | ||
| + | :::{| | ||
| + | | A<sub>s,erf</sub>... || Gesamtquerschnittsfläche der Stäbe, welche nicht Abgestuft wurden/ bzw. weiter durchlaufen | ||
| + | |- | ||
| + | | A<sub>s,vorh</sub>... || Gesamtquerschnittsfläche aller vorhandenen Stäbe | ||
| + | |} | ||
| − | + | Mithilfe der zuvor bestimmten Stahlspannung lässt sich die Verankerungslänge über die dafür allgemeingültigen Formeln bestimmen. | |
| + | An den Stellen, an welchen nach der Abstufung keine Stäbe und somit auch keine zu verankernden Kräfte mehr vorhanden sind (<math>\sigma_\mathrm{sd} =0</math>), ist die Mindestverankerungslänge maßgebend. | ||
| − | + | Da außerhalb von Auflagern i.d.R. genügend Platz ist, werden die endenden Stäbe i.d.R. mit geradem Stabende verankert. | |
| − | [[Verankerung | + | [[Verankerung außerhalb von Auflagern (Bsp.)|Berechnungsbeispiel zur Verankerung außerhalb von Auflagern]] |
<br /> | <br /> | ||
| − | + | == Verankerung am Kragarmende == | |
| − | |||
| − | |||
| − | |||
| + | [[Datei:Verankerung am Einzelfundament (Bsp.) 2.JPG|300px|right]] | ||
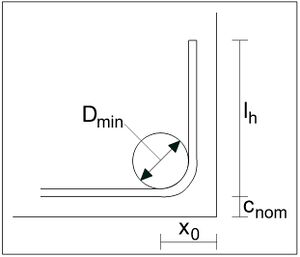
| − | [[ | + | Für die Verankerungslänge am Kragarmende gibt es keine expliziten Berechnungsvorschriften. Sie wird in der Regel in der Literatur nicht nachgewiesen. Die Bewehrung wird in der Regel am Kragarmende abgebogen, bei der Länge des Winkelhakenschenkels gehen verschiedene Programme aber unterschiedlich vor. Eine konkrete Möglichkeit der Berechnung ist der Ansatz über das Verschieben der Momentenlinie mithilfe [[Versatzmaß | Versatzmaßes]]. Die Verankerungslänge beginnt am Anfang der Biegung (Hälfte des Mindestbiegerollendurchmessers) im Abstand <math>x_0</math> vom Rand. Das Moment an der Stelle <math>x_0</math> lässt sich mithilfe der folgenden Gleichung ermitteln: |
| − | < | + | <math>M_{Ed,x_0}=\frac{p_{Ed}\cdot(x_0+a_l)^2}{2}</math> |
| − | + | Die zu verankernde Zugkraft resultiert anschließend aus folgender Gleichung: | |
| − | + | <math>F_{sd}=\frac{M_{Ed,x_0}}{z}</math>. | |
[[Verankerung am Kragarmende (Bsp.)|Berechnungsbeispiel zur Verankerung am Kragarmende]] | [[Verankerung am Kragarmende (Bsp.)|Berechnungsbeispiel zur Verankerung am Kragarmende]] | ||
| − | + | <br /> | |
| + | == Verankerung am Rand von Einzelfundamenten == | ||
| + | Für die Verankerung der Bewehrung am Rand von Einzelfundamenten bietet der EC 2 ein [[Verankerung am Einzelfundament (Modell)|eigenes Berechnungsmodell]]. Dieses Modell findet in der Praxis kaum Anwendung, da es nur für gerade Stabenden benutzbar ist. Im Allgemeinen wird die Bewehrung am Rand von Einzelfundamenten aber als ein Winkelhaken mit konstruktivem Querstab am Ende ausgebildet. Um für diese Konstruktion die Verankerungslänge zu bestimmen, kann wie beim Kragarmende der Ansatz über das Verschieben der Momentenlinie durch das Versatzmaß genutzt werden, auch hier beginnt die Verankerungslänge am Beginn der Biegung. | ||
[[Verankerung am Einzelfundament (Bsp.)|Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten]] | [[Verankerung am Einzelfundament (Bsp.)|Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten]] | ||
| + | <br /> | ||
| − | + | == Verankerung an Konsolen == | |
Die Zugkräfte in Konsolen werden generell über eine bis drei Schlaufen aufgenommen. | Die Zugkräfte in Konsolen werden generell über eine bis drei Schlaufen aufgenommen. | ||
| − | Die Verankerung | + | Die Verankerung der Zugbewehrung in Konsolen gleicht dem Ablauf am Endauflager. Bei der Bemessung von Konsolen wird die benötigte Bewehrungsmenge unmittelbar an der zu verankernden Stelle bestimmt, damit ist <math>A_{s,erf}</math> bekannt. Zu beachten ist, dass die Verankerungslänge an der der Stütze zugewandten Seite der Auflagerplatte beginnt. |
[[Verankerung an Konsolen (Bsp.)|Berechnungsbeispiel zur Verankerung an Konsolen]] | [[Verankerung an Konsolen (Bsp.)|Berechnungsbeispiel zur Verankerung an Konsolen]] | ||
| + | |||
| + | = Quellen = | ||
| + | |||
| + | <references /> | ||
| + | <br /> | ||
| + | |||
| + | {{Seiteninfo | ||
| + | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | ||
| + | |Status = Seite fertig, ungeprüft | ||
| + | }} | ||
| + | |||
| + | |||
| + | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | ||
Aktuelle Version vom 26. Mai 2024, 14:41 Uhr
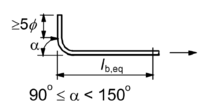
Die Verankerungslänge bezeichnet den Abschnitt am Ende eines Bewehrungsstabes, in dem die am Beginn der Verankerungslänge wirkende Zug- oder Druckkraft vollständig über Verbund in den Beton eingeleitet wird. Ziel der Bemessung der Verankerungslänge ist, dass keine Überschreitung der Trägfähigkeit der Betonkonsole und der Zugfestigkeit des Betons in Querrichtung stattfindet.
Allgemeines
Endet ein Stab sind die Zugkräfte am Stabende im beton zu verankern. Die Verankerung kann über Verbund oder mechanische Verbindungsmittel z.B. Ankerplatten erfolgen. Die Verankerung über Verbund ist die einfachste und wirtschaftlichste Methode, Verankerungen mit mechanischen Verbindungsmitteln sind nur in Sonderfällen sinnvoll und sollen nicht Thema dieser Seite sein. Die Sicherstellung einer ausreichenden Verankerungslänge gehört zu den notwendigen Nachweisen eines Bauteils und gliedert sich in den Arbeitsabschnitt "konstruktive Durchbildung der Bewehrung" ein.
Verbund zwischen Beton und Stahl
Die Übertragung von Kräften zwischen Beton und Bewehrungsstahl erfolgt über den Haft-, Reib- und Formverbund, den größten Anteil an der Kraftübertragung hat hierbei der Formverbund. Da bei der Berechnung auch nur der Formverbund berücksichtigt wird, wird auf den Haft- und Reibverbund im folgenden nicht näher eingegangen.
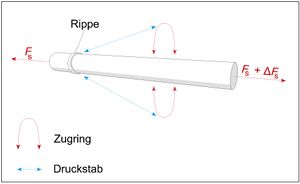
Bei dem genormten Betonstahl wird der Formverbund durch eine Oberflächenprofilierung in Form von Ripppen sichergestellt. Haupteinflussfaktoren auf den Formverbund sind die Form und Neigung der Rippen, die Rippenhöhe und der Rippenabstand. Bei geringen Relativverschiebungen zwischen Bewehrung und Beton stützen sich die Rippen auf dem Beton ab, eine Art Betonkonsole entsteht.
Aufgrund der Anordnung und Form der Rippen findet die Kraftübertragung in Form von ringförmigen schrägen Betondruckstreben statt. Aus Gleichgewichtsgründen bilden sich außerdem Zugspannungsringe senkrecht zur Stabachse.[1] Damit sich diese Zugspannungen aufgenommen werden können, muss eine ausreichende Betondeckung vorhanden sein. Eine zu geringe Betondeckung oder ein zu geringer Stababstand können Längsrisse parallel zur Stabachse zur Folge haben und damit die Verbundwirkung beeinträchtigen.[2]. Die Tragfähigkeit der Verankerung ist maßgeblich davon abhängig ob die Rissbildung infolge Querzugspannungen im Verankerungsbereich verhindert wird oder nicht [3].
Wegen der Querzugspannungen ist im Verankerungsbereich grundsätzlich Querbewehrung anzuordnen. Die in der Norm geforderte Querbewehrung ist in der Regel allerdings bereits durch die Mindestquerbewehrung bei Platten oder die Mindestquerkraftbewehrung bei Balken vorhanden,
Verbundfestigkeit
Die Größe der aufnehmbaren Verbundspannung wird als Verbundfestigkeit bezeichnet. Sie ist abhängig von der Oberflächenbeschaffenheit des Bewehrungsstabs und der Betonzugfestigkeit. Die Berechnung der Verbundfestigkeit kann mit folgender Gleichung erfolgen, die Gleichung ist nur für Betonstahl nach DIN EN 10080 [4] anwendbar, eine Anwendung für Stäbe mit anderen Eigenschaften z.B. glatte Bewehrungsstäbe ist nicht zulässig.
wobei:
ein Beiwert für die Verbundbedingungen ein Beiwert für große Stabdurchmesser der 5 %-Quantil-Wert der charakteristischen Betonzugfestigkeit der Teilsicherheitsbeiwert für die Betonfestigkeit
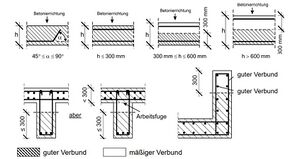
Mit dem Beiwert wird die Lage der Bewehrung im Bauteil berücksichtigt. Abhängig von der Lage wird zwischen guten und mäßigen Verbundbedingungen unterschieden. Mäßige Verbundbedigungen entstehen, wenn während des Verdichtens Luft und Wasser im Beton nach oben transportiert werden und sich unter oben liegenden Stäben ansammeln. Nach der Aushärtung des Betons bilden sich hier Poren oder Ablösungen, so dass der Verbund zwischen Beton und Stahl in diesem Bereich beeinträchtigt ist.
Als Stäbe mit guten Verbundbedigungen gelten Stäbe, welche sich während des Betonierens im unteren Bereich (vgl. Grafik) des Bauteils befinden sowie Stäbe mit einer Neigung >45° bezogen auf die Betonierrichtung. Nähere Informationen zu den Verbundbedingungen können der Grafik entnommen werden. Die Werte für werden im EC2 [5] folgendermaßen definiert:
für gute Verbundbedingungen für mäßige Verbundbedingungen
Der Beiwert berücksichtigt sehr große Stabdurchmesser. Ab einem Grenzwert von Øs = 32 mm nimmt die Verbundfestigkeit bei sonst gleich bleibenden Bedingungen aufgrund der erhöhten Spaltrissgefahr ab. Der Beiwert wird berechnet mit
für Øs ≤ 32 mm für Øs > 32 mm
Die Zugfestigkeit ist auf die Betondruckfestigkeit zurückführbar. Am einfachsten ist es daher, Tabellen zu benutzen, aus denen die Zugfestigkeit bzw. die Verbundfestigkeit in Abhängigkeit von ablesbar sind.[6]. Da der Beton mit zunehmender Festigkeit spröder wird, wird die Betonzugfestigkeit für die Ermittlung der Verbundfestigkeit auf den Wert für C60/75 begrenzt.
Einflussfaktoren auf die Verankerungslänge
Im folgenden wird auf Faktoren eingegangen, welche die Verankerungslänge beeinflussen:
Kleine Herleitung der Verankerungslänge
Im Zuge der Bemessung eines Bauteils wird die nötige Bewehrung bereichsweise für die jeweils maximalen auftretenden Schnittgrößen bestimmt. In der anschließenden konstruktiven Durchbildung wird dann zum Beispiel im Rahmen der Zugkraftdeckung die ermittelte Zugbewehrung dem tatsächlichen Momentenverlauf angepasst und abgestuft. Die so entstehenden Stabenden können nicht direkt an dem Punkt, an dem sie rechnerisch nicht mehr benötigt werden, enden. Vielmehr muss die an diesem Punkt noch im Stab vorhandene Zugkraft im Beton „verankert“ werden, weshalb dieser zusätzliche Stababschnitt als Verankerungslänge bezeichnet wird.
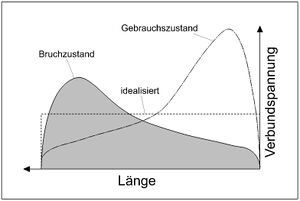
Bei niedriger Beanspruchung ist der Beton an der Stelle der Lasteinleitung ungeschädigt und die Verbundspannung dementsprechend hoch. Erhöht sich die Belastung, so wird der Beton zunächst an der Lasteinleitungsstelle geschädigt (plastisch deformiert), wodurch sich die Verbundspannung in die vorher weniger beanspruchten Bereiche umlagert.[7] In der Berechnung wird dieses komplexe Umlagerungsverhalten nicht berücksichtigt und die Verbundspannung wird als über die Verankerungslänge und den Stabumfang konstant angesetzt.
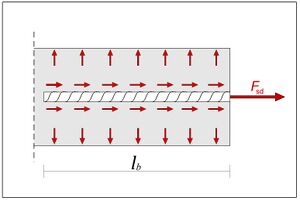
In der dargestellten Skizze muss die Zugkraft vom Stab in den Beton mittels Verbundspannung übertragen werden. Aus Gleichgewichtsgründen gilt nun, dass die zu verankernde Zugkraft kleinergleich der Verbundfestigkeit multipliziert mit der Mantelfläche des Stabes sein muss, also:
Der Umfang des Bewehrungsstabes wird berechnet mit
Die Gleichung für umgestellt nach der benötigten ("required") Verankerungslänge ergibt
Die bisher unbekannte Zugkraft ist das Produkt von Stahlspannung und Bewehrungsfläche . Die Bewehrungsfläche eines Stabs ist . Eingesetzt in die Gleichung der Verankerungslänge ergibt sich
Diese Gleichung wird auch als Grundwert der Verankerungslänge bezeichnet. Wenn im Verankerungsbereich nicht die volle Stahlspannung ausgenutzt wird, darf die Verankerungslänge proportional zum Verhältnis von vorhandener zu erforderlicher Bewehrung reduziert werden. Diese Abminderung wird i.d.R. im Rahmen der Spannungsermittlung berücksichtigt:
Formen und Beiwerte der Verankerungslänge
Bemessungswert der Verankerungslänge
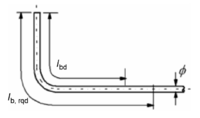
Der Bemessungswert der Verankerungslänge wird aus dem Grundwert der Verankerungslänge abgeleitet und misst die Länge vom Beginn der Verankerungslänge bis zum Stabende. Die Formel hierfür ist
Ersatzverankerungslänge
Alternativ zur Bestimmung der tatsächlichen, gegebenenfalls gebogenen Verankerungslänge kann vereinfacht die gerade Stablänge ermittelt werden; diese misst die Länge vom Ende der Biegeform bis zum Beginn der Verankerungslänge. Die Formel hierfür lautet
Die Ermittlung von ist der Regelfall bei der Ermittlung der Verankerungslänge.
Beiwerte der Verankerungslänge
Bei der Ermittlung des Bemessungswerts der Verankerungslänge oder der Ersatzverankerungslänge aus dem Grundwert der Verankerungslänge kommen einige Beiwerte zum Einsatz. Diese sind wie folgt:
| Beiwert | Bedeutung |
|---|---|
| - Beiwert für Formgebung | |
| - Beiwert für Mindestbetondeckung | |
| - Beiwert für nicht angeschweißte Querbewehrung | |
| - Beiwert für angeschweißte Querbewehrung | |
| - Beiwert für Querdruck |
Übersicht über die Beiwerte
- Formgebung:
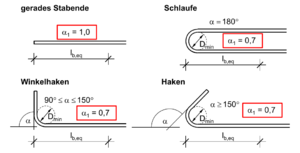
Die Verankerungslänge kann durch abgebogene Stabenden z.B. Haken, Winkelhaken oder Schlaufen verkürzt werden, da Teile der Zugkraft durch Umlenk-bzw. Kontaktpressung aufgenommen werden [3]. Voraussetzung hierfür ist, dass die entstehenden Spaltzugkräfte infolge der Umlenkung durch den Beton aufgenommen werden können. Ist dies nicht der Fall kann die positive Wirkung von abgebognen Stabenden dennoch angesetzt werden, wenn eine enge Verbügelung im Bereich der Abbiegung angeordnet wird.
Bei der Verwendung von Schlaufen besteht zusätzlich die Möglichkeit, unter Einhalten von und eines Biegerollendurchmessers , den Beiwert auf zu reduzieren.
Die Verankerung von Druckstäben mit abgebogenem Stabende ist grundsätzlich unzulässig, da die entstehenden Kräfte zu einer Absprengung der Betondeckung führen können. Auch Stäbe mit einem Durchmesser >32mm dürfen nur mit geradem Stabende verankert werden.
- Mindestbetondeckung:
Der Beiwert für die Mindestbetondeckung erlaubt theoretisch eine Reduzierung auf
In Deutschland ist dieser Beiwert aus der Formel zur Ermittlung des Bemessungswerts der Verankerungslänge gestrichen. Grund hierfür ist, dass eine größere Betondeckung zwar die Entstehung von Spaltrissen verhindert, die Sicherheit gegen Herausziehen der Bewehrung aber nicht erhöht. Würde die Verankerungslänge mit diesem Beiwert reduziert, würde der Versagensfall Herausziehen nicht ausreichend berücksichtigt bzw. unterschätzt. Die Berücksichtigung dieses Bwiwerts liegt somit auf der unsicheren Seite.
- Nicht angeschweißte Querbewehrung:
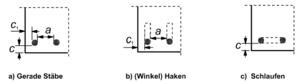
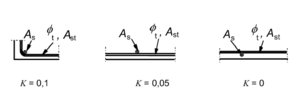
Der Beiwert betrachtet den günstigen Einfluss einer nicht angeschweißten Querbewehrung im Verankerungsbereich. Dieser gilt allerdings nur, wenn die verwendete Querbewehrungsmenge die Mindestquerbewehrungsmenge übersteigt. Bestimmt wird der Beiwert mit
Dabei ist
| die Querschnittsfläche der Querbewehrung innerhalb der Verankerungslänge | |
| die Querschnittsfläche der Mindestbewehrung | |
| die Querschnittsfläche des größten einzelnen verankerten Stabs | |
| Beiwert entsprechend des Bildes |
Für Druckstäbe gilt generell .
- Angeschweißte Querstäbe:
Die Anwesenheit angeschweißter Querstäbe hat aus dem gleichen Grund wie die Stabform einen positiven Effekt auf die Verankerungslänge, da Teile der Zugkraft durch Umlenk-bzw. Kontaktpressung aufgenommen werden[3]. Werden die angegebenen Bedingungen eingehalten, so gilt sowohl für Zug- als auch für Druckstäbe .
- Querdruck:
Der Beiwert betrachtet den Einfluss von Querdruck oder -zug im Verankerungsbereich. Unter Annahme eines Querdrucks senkrecht zur Verankerungsebene berechnet sich der Beiwert als
Für bestimmte Situationen gibt es festgelegte Werte für :
| - bei Querzug senkrecht zur Verankerungsebene | |
| - bei direkter Lagerung | |
| - bei einer allseitig durch Bewehrung gesicherten Betondeckung von mindestens |
Mindestverankerungslänge
Die Mindestverankerungslänge soll sicherstellen, dass trotz Verlegeungenauigkeiten eine ausreichende Verankerungslänge vorhanden ist. Außerdem soll das Maß, um das die Verankerungslänge durch Zulagbewehrung reduziert werden kann, begrenzt werden.
Für Zugstäbe ist die Mindestverankerungslänge definiert als
Für Druckstäbe gilt
Am Zwischenauflager gilt in Deutschland vereinfachend
Nachweis-Situationen der Verankerungslänge
Die verschiedenen Situationen der Verankerungslänge unterscheiden sich vor allem in der Ermittlung der erforderlichen Bewehrungsmenge an der jeweiligen Stelle. Darüber hinaus gelten gegebenenfalls besondere Regeln für die Bestimmung von , und .
Verankerung am Endauflager
Zunächst muss die Randzugkraft, d.h. die Zugkraft am Endauflager bestimmt werden:
VEd... Bemessungswert der einwirkenden Querkraft al... Versatzmaß aus Zugkraftdeckung z... Hebelarm der inneren Kräfte NEd... Bemessungswert der einwirkenden Normalkraft
Anschließend kann die erforderliche Bewehrungsmenge und daraus die Stahlspannung ermittelt werden.
fyd... Bemessungswert der Stahlstreckgrenze
As,vorh... Querschnittsfläche der ins Auflager geführten Bewehrungsstäbe
Mithilfe der zuvor bestimmten Stahlspannung lässt sich die Verankerungslänge über die dafür allgemeingültigen Formeln bestimmen.
Berechnungsbeispiel zur Verankerung am Endauflager
Verankerung am Zwischenauflager
Die am Zwischenauflager endende Feldbewehrung liegt i.d.R im Druckbereich. Deshalb ist sie in vielen Fällen rechnerisch nicht nötig, es gilt , gleiches gilt damit auch für und . Aus diesem Grund ist am Zwischenauflager maßgebend. Die Verankerungslänge am Zwischenauflager beginnt an der Auflagerkante.
Da es sich hier meistens um Druckstäbe handelt sind abgebogenen Stabenden nicht zulässig.
Berechnungsbeispiel zur Verankerung am Zwischenauflager
Verankerung außerhalb von Auflagern
Abseits der Auflager eines Balkens enden Bewehrungsstäbe im Kontext der Zugkraftdeckung. Ab der Stelle an der sie nicht mehr erforderlich sind, sind Stäbe zu verankern. Hier sind erforderliche und vorhandene Bewehrung unmittelbar bekannt.
Ermittlung der Stahlspannung am rechnerischen Endpunkt E:
As,erf... Gesamtquerschnittsfläche der Stäbe, welche nicht Abgestuft wurden/ bzw. weiter durchlaufen As,vorh... Gesamtquerschnittsfläche aller vorhandenen Stäbe
Mithilfe der zuvor bestimmten Stahlspannung lässt sich die Verankerungslänge über die dafür allgemeingültigen Formeln bestimmen.
An den Stellen, an welchen nach der Abstufung keine Stäbe und somit auch keine zu verankernden Kräfte mehr vorhanden sind (), ist die Mindestverankerungslänge maßgebend.
Da außerhalb von Auflagern i.d.R. genügend Platz ist, werden die endenden Stäbe i.d.R. mit geradem Stabende verankert.
Berechnungsbeispiel zur Verankerung außerhalb von Auflagern
Verankerung am Kragarmende
Für die Verankerungslänge am Kragarmende gibt es keine expliziten Berechnungsvorschriften. Sie wird in der Regel in der Literatur nicht nachgewiesen. Die Bewehrung wird in der Regel am Kragarmende abgebogen, bei der Länge des Winkelhakenschenkels gehen verschiedene Programme aber unterschiedlich vor. Eine konkrete Möglichkeit der Berechnung ist der Ansatz über das Verschieben der Momentenlinie mithilfe Versatzmaßes. Die Verankerungslänge beginnt am Anfang der Biegung (Hälfte des Mindestbiegerollendurchmessers) im Abstand vom Rand. Das Moment an der Stelle lässt sich mithilfe der folgenden Gleichung ermitteln:
Die zu verankernde Zugkraft resultiert anschließend aus folgender Gleichung:
.
Berechnungsbeispiel zur Verankerung am Kragarmende
Verankerung am Rand von Einzelfundamenten
Für die Verankerung der Bewehrung am Rand von Einzelfundamenten bietet der EC 2 ein eigenes Berechnungsmodell. Dieses Modell findet in der Praxis kaum Anwendung, da es nur für gerade Stabenden benutzbar ist. Im Allgemeinen wird die Bewehrung am Rand von Einzelfundamenten aber als ein Winkelhaken mit konstruktivem Querstab am Ende ausgebildet. Um für diese Konstruktion die Verankerungslänge zu bestimmen, kann wie beim Kragarmende der Ansatz über das Verschieben der Momentenlinie durch das Versatzmaß genutzt werden, auch hier beginnt die Verankerungslänge am Beginn der Biegung.
Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten
Verankerung an Konsolen
Die Zugkräfte in Konsolen werden generell über eine bis drei Schlaufen aufgenommen. Die Verankerung der Zugbewehrung in Konsolen gleicht dem Ablauf am Endauflager. Bei der Bemessung von Konsolen wird die benötigte Bewehrungsmenge unmittelbar an der zu verankernden Stelle bestimmt, damit ist bekannt. Zu beachten ist, dass die Verankerungslänge an der der Stütze zugewandten Seite der Auflagerplatte beginnt.
Berechnungsbeispiel zur Verankerung an Konsolen
Quellen
- ↑ Vgl. Avak, Ralf: Stahlbetonbau in Beispielen. DIN 1045. Teil 1, Köln 2007 (5. Auflage), S. 53.
- ↑ Vgl. Wommelsdorff, Otto; Albert, Andrej; Fischer, Jürgen: Stahlbetonbau. Bemessung und Konstruktion. Teil 1, Köln 2017 (11. Auflage), S. 87.
- ↑ Hochspringen nach: 3,0 3,1 3,2 Zilch,K., Zehetmaier,G., Bemessung im konstruktiven Betonbau, 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006
- ↑ DIN EN 10080, Stahl für die Bewehrung von Beton - Schweißgeeigneter Betonstahl - Allgemeines, Beuth-Verlag, 2005
- ↑ Hochspringen nach: 5,0 5,1 DIN EN 1992-1-1, Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2011
- ↑ Albert, Andrej (Hg.): Schneider Bautabellen für Ingenieure, Köln 2020 (24. Auflage), S. 5.108.
- ↑ Vgl. König, Gert; Tue, Nguyen Viet: Grundlagen des Stahlbetonbaus. Einführung in die Bemessung nach DIN 1045-1, Wiesbaden 2003 (2. Auflage), S. 416.
Seiteninfo
|