Momenten-Krümmungs-Beziehungen (Bsp.): Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) |
EWill (Diskussion | Beiträge) K |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
* C 20/25 | * C 20/25 | ||
* <math>E_{cm}=10000\frac{N}{mm^2}=1000\frac{kN}{cm^2}</math> (Mit der Berücksichtigung von Kriecheinflüssen) | * <math>E_{cm}=10000\frac{N}{mm^2}=1000\frac{kN}{cm^2}</math> (Mit der Berücksichtigung von Kriecheinflüssen) | ||
| − | + | * Kurzzeitbelastung | |
| + | |||
=Festigkeiten= | =Festigkeiten= | ||
<math>f_{ck}=20\frac{N}{mm^2}\qquad\qquad f_{yk}=500\frac{N}{mm^2}</math> | <math>f_{ck}=20\frac{N}{mm^2}\qquad\qquad f_{yk}=500\frac{N}{mm^2}</math> | ||
| Zeile 54: | Zeile 55: | ||
Ermittlung des Streckgrenzenmoments nach Schmitz <ref name="schmitz02">Schmitz: Statik - in Stahlbetonbau aktuell 2002 | Ermittlung des Streckgrenzenmoments nach Schmitz <ref name="schmitz02">Schmitz: Statik - in Stahlbetonbau aktuell 2002 | ||
</ref>: | </ref>: | ||
| + | |||
| + | [[File:Momenten-Krümmungs-Beziehungen (Bsp.)_5.jpg|right|thumb|400px|Ermittlung des Streckgrenzenmoments nach Schmitz<ref name="schmitz02"></ref>]] | ||
<math>\omega_{II}=\frac{19,64}{35\cdot70}\cdot\frac{55}{1,445}</math> | <math>\omega_{II}=\frac{19,64}{35\cdot70}\cdot\frac{55}{1,445}</math> | ||
| Zeile 69: | Zeile 72: | ||
<math>|0,1\cdot\varepsilon_c2|=0,19\cdot10^{-3}</math> | <math>|0,1\cdot\varepsilon_c2|=0,19\cdot10^{-3}</math> | ||
| − | <math>|\ | + | <math>|\varepsilon_{c2}|=1,9\cdot10^{-3}</math> |
===Krümmung=== | ===Krümmung=== | ||
| Zeile 97: | Zeile 100: | ||
===Krümmung=== | ===Krümmung=== | ||
| − | <math>\ | + | <math>\kappa_t=\frac{5,38\cdot10^{-3}+3,5\cdot10^{-3}}{70}=126,86\cdot10^{-6}\frac{1}{cm}=126,86\cdot10^{-4}\frac{1}{m}</math> |
| + | |||
| + | ==Darstellung der Momenten-Krümmungs-Beziehungen== | ||
| + | |||
| + | [[File:Momenten-Krümmungs-Beziehungen (Bsp.)_2.jpg|400px|Darstellung der Momenten-Krümmungs-Beziehungen ohne Mitwirkung des Betons zwischen den Rissen]] | ||
=Ermittlung der Momenten-Krümmungs-Beziehungen ohne Mitwirkung des Betons zwischen den Rissen= | =Ermittlung der Momenten-Krümmungs-Beziehungen ohne Mitwirkung des Betons zwischen den Rissen= | ||
| Zeile 121: | Zeile 128: | ||
==Krümmung im gerissenen Zustand bei Erreichen der Streckgrenze des Betonstahls== | ==Krümmung im gerissenen Zustand bei Erreichen der Streckgrenze des Betonstahls== | ||
===Dehnungen=== | ===Dehnungen=== | ||
| + | |||
| + | Ermittlung der Stahldehnung im gerissenen Zustand unter den Schnittgrößen, die zur Erstrissbildung führen: | ||
| + | |||
| + | <math>\alpha_e=\frac{E_s}{E_{c,eff}}=\frac{200000}{10000}=20</math> | ||
| + | |||
| + | <math>x=\frac{\alpha_e\cdot A_{s1}}{b}\cdot\left(-1+\sqrt{1+\frac{2\cdot b\cdot d}{\alpha_e\cdot A_{s1}}}\right)</math> | ||
| + | |||
| + | |||
| + | <math>x=\frac{20\cdot 19,64}{35}\cdot\left(-1+\sqrt{1+\frac{2\cdot 35\cdot 70}{20\cdot 19,64}}\right)=29,97cm</math> | ||
| + | |||
| + | <math>z=d-\frac{x}{3}=70-\frac{29,97}{3}=60cm</math> | ||
| + | |||
| + | <math>\sigma_{s,cr2}=\frac{M_{cr}}{z\cdot A_{s1}}=\frac{7219}{60\cdot19,64}=6,12\frac{kN}{cm^2}</math> | ||
| + | |||
| + | <math>\varepsilon_{s,cr2}=\frac{\sigma_{s,cr2}}{E_s}=\frac{6,12}{20000}=0,306\cdot 10^{-3}</math> | ||
| + | |||
| + | Ermittlung der mittleren Stahldehnung an der Streckgrenze: | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{s2}-\beta_t\cdot\left(\varepsilon_{s,cr2}-\varepsilon_{s,cr1}\right)</math> | ||
| + | |||
| + | <math>\varepsilon_{sy}=\varepsilon_{s2}=\frac{55}{20000}=2,75\cdot10^{-3}</math> | ||
| + | |||
| + | <math>\beta_t=0,4</math> (Kurzzeitbelastung) | ||
| + | |||
| + | <math>\varepsilon_{smy}=2,75\cdot 10^{-3}-0,4\cdot (0,306\cdot 10^{-3}-0,191\cdot 10^{-3})</math> | ||
| + | |||
| + | <math>\varepsilon_{smy}=2,704\cdot10^{-3}</math> | ||
| + | |||
| + | Die Betonstauchung ändert sich durch die Mitwirkung des Betons zwischen den Rissen nicht: | ||
| + | |||
| + | <math>|\varepsilon_{c2}|=1,9\cdot10^{-3}</math> | ||
| + | |||
===Krümmungen=== | ===Krümmungen=== | ||
| + | |||
| + | <math>\kappa_{my}=\frac{2,704\cdot 10^{-3}+1,9\cdot 10^{-3}}{70}=65,77\cdot 10^{-6}\frac{1}{cm}=65,77\cdot 10^{-4}\frac{1}{m}</math> | ||
| + | |||
==Krümmung im gerissenen Zustand unter den Bruchschnittgrößen== | ==Krümmung im gerissenen Zustand unter den Bruchschnittgrößen== | ||
===Dehnungen=== | ===Dehnungen=== | ||
| + | |||
| + | <math>\varepsilon_{sm}=\varepsilon_{sy}-\beta_t\cdot\left(\varepsilon_{s,cr2}-\varepsilon_{s,cr1}\right)+\delta_t\cdot\left(1-\frac{\sigma_{sr}}{f_y}\right)\cdot\left(\varepsilon_{s2}-\varepsilon_{sy}\right)</math> | ||
| + | |||
| + | <math>\varepsilon_{s2}=\varepsilon_{st}=5,38\cdot10^{-3}</math> | ||
| + | |||
| + | <math>\varepsilon_{smt}=2,75\cdot 10^{-3}-0,4\cdot (0,306\cdot 10^{-3}-0,191\cdot 10^{-3})+0,6\cdot \left(1-\frac{0,191\cdot 10^{-3}\cdot 20000}{55}\right)\cdot \left(5,38\cdot 10^{-3}-2,75\cdot 10^{-3}\right)</math> | ||
| + | |||
| + | <math>\varepsilon_{smt}=4,17\cdot10^{-3}</math> | ||
| + | |||
| + | Die Betonstauchung ändert sich durch die Mitwirkung des Betons zwischen den Rissen nicht: | ||
| + | |||
| + | <math>|\varepsilon_{ct}|=3,5\cdot10^{-3}</math> | ||
| + | |||
===Krümmungen=== | ===Krümmungen=== | ||
| + | |||
| + | <math>\kappa_{mt}=\frac{4,17\cdot 10^{-3}+3,5\cdot 10^{-3}}{70}=109,6\cdot 10^{-6}\frac{1}{cm}=109,6\cdot 10^{-4}\frac{1}{m}</math> | ||
| + | |||
| + | ==Darstellung der Momenten-Krümmungs-Beziehungen== | ||
| + | |||
| + | [[File:Momenten-Krümmungs-Beziehungen (Bsp.)_3.jpg|400px|Darstellung der Momenten-Krümmungs-Beziehungen ohne Mitwirkung des Betons zwischen den Rissen]] | ||
| + | |||
| + | =Vergleich der Momenten-Krümmungs-Beziehungen mit und ohne Mitwirkung des Betons zwischen den Rissen= | ||
| + | |||
| + | [[File:Momenten-Krümmungs-Beziehungen (Bsp.)_4.jpg|400px|Vergleich der Momenten-Krümmungs-Beziehungen mit und ohne Mitwirkung des Betons zwischen den Rissen]] | ||
| + | |||
=Quellen= | =Quellen= | ||
<references /> | <references /> | ||
Aktuelle Version vom 10. August 2024, 21:23 Uhr
Auf dieser Seite werden beispielhaft die Momenten-Krümmungs-Beziehungen ermittelt, die Theorie hierfür wird auf einer gesonderten Seite dargestellt (vgl. Momenten-Krümmungs-Beziehungen. Die Berechnungen werden vergleichend mit und ohne Mitwirkung des Betons zwischen den Rissen durchgeführt.
Aufgabenstellung
Für einen Balken mit Rechteckquerschnitt und gegebener Bewehrung sollen die Momenten-Krümmungs-Beziehungen berechnet werden. Als Festigkeiten sind die rechnerischen Mittelwerte anzusetzen
- b/h=35cm/75cm
- d=70cm
- B500A
- Längsbewehrung: 4⌀25 (As,vorh=19,64cm²)
- C 20/25
- (Mit der Berücksichtigung von Kriecheinflüssen)
- Kurzzeitbelastung
Festigkeiten
Ermittlung der Momenten-Krümmungs-Beziehungen ohne Mitwirkung des Betons zwischen den Rissen
ungerissener Zustand
Moment
Dehnungen
Krümmung
Krümmung im gerissenen Zustand bei Erreichen der Streckgrenze des Betonstahls
Moment
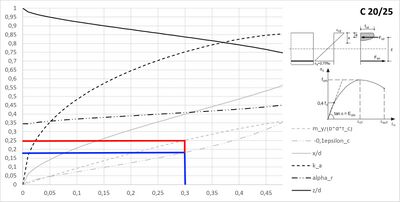
Ermittlung des Streckgrenzenmoments nach Schmitz [1]:
Dehnungen
Krümmung
Krümmung im gerissenen Zustand unter den Bruchschnittgrößen
Moment
Das Moment wird mit den ω-Tafeln mit dem rechnerischen Mittelwert der Zug- bzw. Druckfestigkeit ermittelt:
Dehnungen
Die Dehnungen werden ebenfalls aus der ω-Tafel abgelesen:
Krümmung
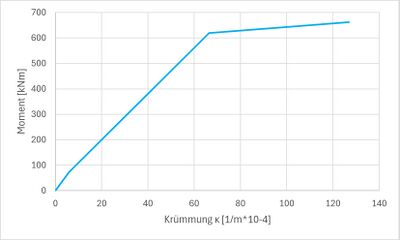
Darstellung der Momenten-Krümmungs-Beziehungen
Ermittlung der Momenten-Krümmungs-Beziehungen ohne Mitwirkung des Betons zwischen den Rissen
Im Vergleich zu den bisherigen Betrachtungen findet bei der Berücksichtigung der Mitwirkung des Betons zwsichen den Rissen eine Unterteilung in den ungerissenen Zustand und die Erstrissbildung statt. Auf die Berücksichtigung wird vereinfachend an dieser Stelle verzichtet.
Die Momente werden im Folgenden nicht erneut ermittelt, da die Mitwirkung des Betons zwischen den Rissen keinen Einfluss auf diese hat.
Die Gleichungen zur Ermittlung der mittleren Stahldehnung können auf der Seite zur Mitwirkung des Betons zwischen den Rissen gefunden werden.
ungerissener Zustand
Dehnungen
Da noch keine Risse vorhanden sind, ändern sich die Dehnungen nicht im Vergleich zur vorherigen Berechnung.
Krümmungen
Da noch keine Risse vorhanden sind, ändert sich die Krümmung nicht im Vergleich zur vorherigen Berechnung.
Krümmung im gerissenen Zustand bei Erreichen der Streckgrenze des Betonstahls
Dehnungen
Ermittlung der Stahldehnung im gerissenen Zustand unter den Schnittgrößen, die zur Erstrissbildung führen:
Ermittlung der mittleren Stahldehnung an der Streckgrenze:
(Kurzzeitbelastung)
Die Betonstauchung ändert sich durch die Mitwirkung des Betons zwischen den Rissen nicht:
Krümmungen
Krümmung im gerissenen Zustand unter den Bruchschnittgrößen
Dehnungen
Die Betonstauchung ändert sich durch die Mitwirkung des Betons zwischen den Rissen nicht:
Krümmungen
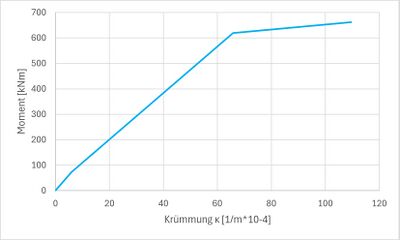
Darstellung der Momenten-Krümmungs-Beziehungen
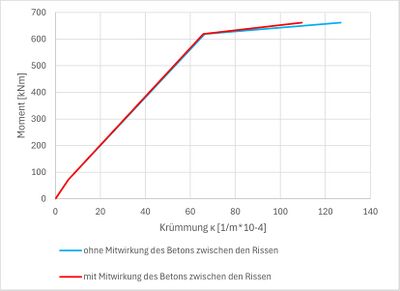
Vergleich der Momenten-Krümmungs-Beziehungen mit und ohne Mitwirkung des Betons zwischen den Rissen
Quellen
Seiteninfo
|