Eigenspannungen: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
== Allgemeines == | == Allgemeines == | ||
Eigenspannungen entstehen immer dann, wenn sich über den Querschnitt verteilt unterschiedliche Dehnungen einstellen. <br/> | Eigenspannungen entstehen immer dann, wenn sich über den Querschnitt verteilt unterschiedliche Dehnungen einstellen. <br/> | ||
| − | Charakteristisch für diese Art der Spannungen ist, dass sich ihre Summe über den Querschnitt immer zu Null ergibt. Zusätzlich dazu werden weder Schnittkräfte erzeugt noch Auflagerreaktionen angrenzender Bauteile hervorgerufen. Außerdem entwickeln sich Eigenspannungen unabhängig vom statischen System und der Bauteillagerung.<ref name = " | + | Charakteristisch für diese Art der Spannungen ist, dass sich ihre Summe über den Querschnitt immer zu Null ergibt. Zusätzlich dazu werden weder Schnittkräfte erzeugt noch Auflagerreaktionen angrenzender Bauteile hervorgerufen. Außerdem entwickeln sich Eigenspannungen unabhängig vom statischen System und der Bauteillagerung.<ref name = "Q1"> Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 9. überarbeitete und erweiterte Auflage. Düsseldorf 2009</ref> |
== Beispiele == | == Beispiele == | ||
| − | [[Datei:Eigenspannungen 1.jpeg|300px|thumb|right|Spannungsverlauf beim Biegen eines Bewehrungsstahles<ref name = " | + | [[Datei:Eigenspannungen 1.jpeg|300px|thumb|right|Spannungsverlauf beim Biegen eines Bewehrungsstahles<ref name = "Q2"> Avak, R.; Conchon, R.; Aldejohann, M.: Stahlbetonbau in Beispielen Teil 1. Grundlagen der Stahlbetonbaubemessung. Bemessung von Stabtragwerken nach EC 2. 7., überarbeitete und aktualisierte Auflage. Köln 2016</ref> ]] |
Im Stahlbetonbau werden Eigenspannungen beispielsweise beim Biegen eines Bewehrungsstahles oder bei Zwangsbeanspruchungen berücksichtigt.<br/> | Im Stahlbetonbau werden Eigenspannungen beispielsweise beim Biegen eines Bewehrungsstahles oder bei Zwangsbeanspruchungen berücksichtigt.<br/> | ||
| − | Wird ein Bewehrungsstahl gebogen, dehnt sich der Querschnitt unterschiedlich stark und beginnt in Teilbereichen zu fließen. Die Eigenspannungen entstehen nach dem Biegen durch die eingeprägte Verformung. Damit der Stahl nicht bis zu seiner Bruchdehnung plastiziert, muss der Biegerollendurchmesser begrenzt werden.<ref name = " | + | Wird ein Bewehrungsstahl gebogen, dehnt sich der Querschnitt unterschiedlich stark und beginnt in Teilbereichen zu fließen. Die Eigenspannungen entstehen nach dem Biegen durch die eingeprägte Verformung. Damit der Stahl nicht bis zu seiner Bruchdehnung plastiziert, muss der Biegerollendurchmesser begrenzt werden.<ref name = "Q2"></ref><br/> |
| − | Bei den Zwangsbeanspruchungen treten Eigenspannungen nur als Resultat des [[Zwangsarten#Unterscheidung in inneren und äußeren Zwang | inneren Zwangs]] auf. Der hierbei entstehende nichtlineare Spannungsanteil wird durch die unterschiedliche Temperatur- bzw. Feuchtigkeitsverteilung über | + | Bei den Zwangsbeanspruchungen treten Eigenspannungen nur als Resultat des [[Zwangsarten#Unterscheidung in inneren und äußeren Zwang | inneren Zwangs]] auf. Der hierbei entstehende nichtlineare Spannungsanteil wird durch die unterschiedliche Temperatur- bzw. Feuchtigkeitsverteilung über den Querschnitt infolge des [[Abfließen der Hydratationswärme | Abfließens der Hydratationswärme]] bzw. des [[Schwinden | Schwindens]] erzeugt.<br/> |
| − | Im [[Zwang - Bauweisen mit wesentlichen Zwangsbeanspruchungen#Spannbetonbauweise | Spannbetonbau]] stellt sich ein Eigenspannungszustand durch das Einbringen der Vorspannung in den Spannstahl ein. Das Spannglied wird durch eine Zugkraft belastet, wodurch in den Betonquerschnitt eine Druckkraft eingeleitet wird.<ref name = " | + | Im [[Zwang - Bauweisen mit wesentlichen Zwangsbeanspruchungen#Spannbetonbauweise | Spannbetonbau]] stellt sich ein Eigenspannungszustand durch das Einbringen der Vorspannung in den Spannstahl ein. Das Spannglied wird durch eine Zugkraft belastet, wodurch in den Betonquerschnitt eine Druckkraft eingeleitet wird.<ref name = "Q3"> Prof. Dr. W. Kaufmann: Vorlesung Stahlbeton II. Vorspannkonzepte. ETH Zürich 2017 </ref> |
== Quellen == | == Quellen == | ||
:''Fachliteratur'' | :''Fachliteratur'' | ||
| − | <references | + | <references/> |
<br /> | <br /> | ||
Aktuelle Version vom 3. April 2019, 09:40 Uhr
Allgemeines
Eigenspannungen entstehen immer dann, wenn sich über den Querschnitt verteilt unterschiedliche Dehnungen einstellen.
Charakteristisch für diese Art der Spannungen ist, dass sich ihre Summe über den Querschnitt immer zu Null ergibt. Zusätzlich dazu werden weder Schnittkräfte erzeugt noch Auflagerreaktionen angrenzender Bauteile hervorgerufen. Außerdem entwickeln sich Eigenspannungen unabhängig vom statischen System und der Bauteillagerung.[1]
Beispiele
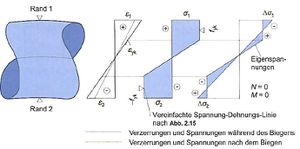
Im Stahlbetonbau werden Eigenspannungen beispielsweise beim Biegen eines Bewehrungsstahles oder bei Zwangsbeanspruchungen berücksichtigt.
Wird ein Bewehrungsstahl gebogen, dehnt sich der Querschnitt unterschiedlich stark und beginnt in Teilbereichen zu fließen. Die Eigenspannungen entstehen nach dem Biegen durch die eingeprägte Verformung. Damit der Stahl nicht bis zu seiner Bruchdehnung plastiziert, muss der Biegerollendurchmesser begrenzt werden.[2]
Bei den Zwangsbeanspruchungen treten Eigenspannungen nur als Resultat des inneren Zwangs auf. Der hierbei entstehende nichtlineare Spannungsanteil wird durch die unterschiedliche Temperatur- bzw. Feuchtigkeitsverteilung über den Querschnitt infolge des Abfließens der Hydratationswärme bzw. des Schwindens erzeugt.
Im Spannbetonbau stellt sich ein Eigenspannungszustand durch das Einbringen der Vorspannung in den Spannstahl ein. Das Spannglied wird durch eine Zugkraft belastet, wodurch in den Betonquerschnitt eine Druckkraft eingeleitet wird.[3]
Quellen
- Fachliteratur
- ↑ Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 9. überarbeitete und erweiterte Auflage. Düsseldorf 2009
- ↑ 2,0 2,1 Avak, R.; Conchon, R.; Aldejohann, M.: Stahlbetonbau in Beispielen Teil 1. Grundlagen der Stahlbetonbaubemessung. Bemessung von Stabtragwerken nach EC 2. 7., überarbeitete und aktualisierte Auflage. Köln 2016
- ↑ Prof. Dr. W. Kaufmann: Vorlesung Stahlbeton II. Vorspannkonzepte. ETH Zürich 2017
Seiteninfo
|
