Heißbemessung Stahlbetonbau

Ein brennendes Gebäude

Die Heißbemessung im Stahlbetonbau bezeichnet den rechnerischen Nachweis von Bauteilen oder Tragwerken aus Stahlbeton, welche durch einen Brand beansprucht werden. Die Bemessungsverfahren der Brandschutznachweise werden im Brandschutzteil des Eurocodes Teil 2, der DIN EN 1992-1-2, geregelt. Die auf dieser Seite behandelten Themen basieren auf den Grundlagen der Heißbemessung.

Materialeigenschaften - Bauteilwiderstände

Bei hohen Temperaturen ändern sich die Materialeigenschaften der Bauteile. Auf der Widerstandsseite müssen dabei die thermischen und die mechanischen Materialeigenschaften betrachtet werden.

Thermische Eigenschaften

Zu den thermischen Eigenschaften eines Materials gehören die spezifische Wärme, die Wärmeleitfähigkeit und die Rohdichte. Diese werden für die Berechnung der Temperaturveränderung innerhalb von Bauteilen aus Beton und Stahl, welche brandbeansprucht sind, benötigt. Hiermit kann die Temperatur in einem bestimmten Punkt des Bauteils bestimmt werden, was wiederum für einen Teil der Heißbemessung von Nöten ist. Außerdem muss die Dehnung infolge der Temperaturänderung des Materials beachtet werden.

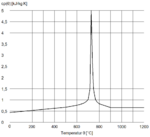
Wärmekapazität

Spezifische Wärme von Beton nach DIN EN 1992-1-2

Spezifische Wärme von Stahl nach DIN EN 1993-1-2

Die ,,spezifische Wärme“ oder auch ,,Wärmekapazität“ genannt, bezeichnet mit c_p(θ) [J/(kg*K)], steht für das Vermögen eines Materials, Wärmeenergie aufzunehmen. Beschrieben wird dies durch die Wärmemenge Q (in Joule), welche zur Erwärmung von 1 kg Masse um 1 K erforderlich ist.

Bei Beton spielt der Feuchtegehalt eine entscheidende Rolle. Da Wasser mehr Energie zum Erwärmen benötigt als Beton, läuft die Erwärmung des Bauteils am Anfang langsamer ab, bis das Wasser verdampft ist.

Im Temperaturbereich von 100 – 200°C kommt es zur Verdampfung von Porenwasser. Die spezifische Wärme steigt aufgrund der dafür verbrauchten Wärmeenergie an. Die benötigte Energiemenge ist dabei von der relativen Betonfeuchte abhängig. Danach ist nur noch der Widerstand des Betons vorhanden.

Auch bei Stahl ändert sich die spezifische Wärmekapazität mit der Temperaturänderung. Im Vergleich mit der von Beton, ist diese jedoch viel geringer. Sie liegt im Durchschnitt bei ca. 0,6 KJ/(kg*K) und erreicht somit nur 50% des Wertes von trockenem Beton. Betonstahl nimmt die Wärme also wesentlich schneller auf.

Aufgrund von Umkristallisationsvorgängen, welche Wärmeenergie in Bindungsenergie umwandeln, steigt die Wärmekapazität zwischen 600 und 800°C stark an. Dieser Einfluss fällt allerdings eher gering aus.

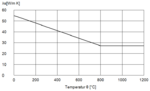
thermische Leitfähigkeit

Wärmeleitfähigkeit von Beton nach DIN EN 1992-1-2

Wärmeleitfähigkeit von Stahl nach DIN EN 1993-1-2

Die Kapazität eines Materials, Wärme zu transportieren, wird als ,,Wärmeleitfähigkeit" oder auch ,,thermische Leitfähigkeit" mit λ [W/(m*K)] bezeichnet. Sie beschreibt die Wärmemenge Q (in Joule), welche in einer bestimmten Zeit, aufgrund eines bestimmten Temperaturunterschiedes, durch einen Körper mit der Länge l und der Fläche A fließt. Damit wird ausgesagt, wie schnell Wärme in das Innere von Bauteilen dringt und wie schnell dieses wieder abkühlt. Sie wird in [(J/s)/(m*K)], bzw. [W/(m*K)] angegeben. Je geringer diese ist, desto besser ist das Dämmvermögen.

Bei Beton ist die thermische Leitfähigkeit stark von den Zuschlägen und dem Temperaturunterschied abhängig. Sie wird mit einem oberen und unteren Grenzwert angegeben. Dabei steht die Kurve 1 für quarzhaltige Zuschläge und die Kurve 2 für kalksteinhaltige Zuschläge. Im nationalen Anhang [2-2] des EC 2-1-2 wird die Verwendung des oberen Grenzwertes vorgeschrieben. Bei Beton nimmt die Wärmeleitfähigkeit mit steigender Temperatur ab. Baustoffe wie Bims oder Blähton können die Leitfähigkeit weiter verringern.

Die Wärmeleitfähigkeit von Stahl liegt zwischen 50 und 30 W/(m*K) und ist damit 25 bis 50 mal so hoch, wie die von Beton. Dies bedeutet, dass der Betonstahl seine Wärme sehr schnell wieder abgibt. In diesem Fall direkt an den Beton, welcher infolge dessen schneller erwärmt wird.

thermische Dehnung

thermische Dehnung von Stahlbeton nach DIN EN 1992-1-2

thermische Dehnung von Stahl nach DIN EN 1993-1-2

Die Abmessungen eines Körpers nehmen bei steigender Temperatur zu. Diese Reaktion wird als Temperaturdehnung ε [Δl/l] bezeichnet. Bei ε handelt es sich um eine grundsätzlich temperaturabhängige Größe.

Bei einer Temperaturerhöhung von Beton, kann es je nach Bestandteil des Betons zu einem teils sprunghaften Volumenanstieg kommen. Ein Beispiel dafür ist Quarz. Wenn es die Temperatur 573°C erreicht, kommt es zum sogenannten Quarzsprung. Dabei nimmt das Quarzvolumen sprunghaft um 0,8 % zu. Der dem Steigungswinkel der Kurve entsprechende Koeffizient α_T liegt je nach Zuschlag zwischen 0,6 und 1,0*10^-5/K. Die Temperaturdehnung für Beton wird mit ε_c(θ) bezeichnet.

Stahl hingegen dehnt sich anders aus als Beton. Der Koeffizient αT liegt für Betonstahl bei ca. 1,3*10^-5/K. Erreicht die Temperatur den Bereich zwischen 750 – 860 °C kommt es zu einer Gefügeumwandlung im Stahl. Die Dehnung von Betonstahl wird mit ε_s(θ) bezeichnet.

Bei Normaltemperatur sind die Unterschiede zwischen Beton und Stahl eher gering. Diese werden mit steigenden Temperaturen jedoch immer größer. Die Materialien dehnen sich unterschiedlich aus, wodurch große innere Spannungen entstehen, welche eine Rissbildung zur Folge haben können.

Rohdichte

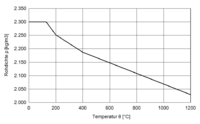Rohdichte von Beton unter Temperatureinfluss

Das Porensystem im Beton bietet Platz für Flüssigkeiten wie zum Beispiel Wasser. Die Rohdichte von Beton, angegeben mit ρ [kg/m³], ist somit vom Wassergehalt des Porensystems abhängig. Allerdings fällt die Veränderung der Dichte bei der Erwärmung von Beton nur relativ gering aus.

Mechanische Eigenschaften

Die temperaturabhängigen Veränderungen der mechanischen Baustoffwerte spiegeln sich in den Spannungs- Dehnungsbeziehungen wider. Diese sind Grundlage der brandschutztechnischen Bauteil- und Tragwerksanalyse. Das Festigkeits- und Verformungsverhalten von Baustoffen bei erhöhten Temperaturen wird im Eurocode 2-1-2 Abschnitt 3 vereinfacht, aber für den Brandschutznachweis ausreichend dargestellt. Anhand der Darstellungsweise des Baustoffverhaltens, wird an die Bemessungsgrundlagen bei Normaltemperatur angeknüpft.

Die charakteristischen Festigkeiten bei Normaltemperatur, f_ck für Beton und f_yk für Stahl, sind dabei Eingangswerte für die Spannungs-Dehnungsbeziehungen unter Temperatureinfluss. Die Materialfestigkeiten und die E-Module von Beton und Stahl ändern sich unter hohen Temperaturen. Schon bei einem geringen Spannungszuwachs nimmt die Dehnung unter hohen Temperaturen deutlich zu. Daraus lässt sich schließen, dass die Festigkeit von Stahl und Beton unter hohen Temperaturen stark abnimmt.

Beton

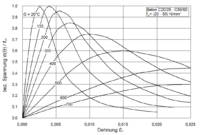Die temperaturanhängigen Spannungs-Dehnungslinien von Beton

Beiwert kc(θ) nach DIN EN 1992-1-2

Bei Beton wird die Beziehung zwischen Spannung und Dehnung mit den zwei Parametern f_c,θ (Druckfestigkeit) und ε_c1,θ (Stauchung) bestimmt. Dazu wird außerdem zwischen kalksteinhaltigen und quarzhaltigen Zuschlagstoffen unterschieden, da diese bei der Wärmeleitfähigkeit und Wärmedehnung eine entscheidende Rolle spielen.

Im Eurocode 2-1-2 werden die Hauptparameter dafür in der Tabelle 3.1 angegeben. Vergleicht man die Werte der kalksteinhaltigen und quarzhaltigen Zuschläge fällt auf, dass die Werte für quarzhaltige Zuschläge geringer ausfallen. Das Diagramm ist daher für die quarzhaltigen Zuschläge aufgestellt.

Für Beton sind die Spannungs-Dehnungslinien mit Hilfe der Einheitstemperaturkurve ermittelt worden. Wird stattdessen ein Naturbrandmodell verwendet, müssen diese entsprechend modifiziert werden.

Durch die Zunahme der Verformungsfähigkeit (Abnahme des E-Moduls) von 2,5‰ Bei 20°C auf 10-20 ‰ bei 600°C, werden aus den Randbereichen Spannungen auf innere Bereiche mit höherer Festigkeit umgelagert. Dies hat eine Reduzierung der Druckfestigkeit zur Folge.

Im Eurocode 2-1-2 gibt es Reduktionsfaktoren zur Berücksichtigung der Abnahme der Betonfestigkeit unter erhöhten Temperaturen. So wird die Abnahme der charakteristischen Druckfestigkeit f_ck durch den Beiwert k_c(θ) berücksichtigt.

Die temperaturabhängigen Spannungs-Dehnungslinien von kalt verformtem Betonstahl (B500)

Beiwert ks(θ) nach DIN EN 1992-1-2

Dieser wird im EC 2-1-2 unter 4.2.4.2 in einem Diagramm beschrieben. Der Einfluss der Zuschläge auf die Festigkeit wird hier noch einmal deutlich erkennbar.

Auch die Zugfestigkeit nimmt mit steigender Temperatur stark ab. Eine Mitwirkung des Betons zwischen Rissen in äußeren Bewehrungslagen ist fast nicht vorhanden. Um auf der sicheren Seite zu liegen, sollte Sie im Regelfall nicht angesetzt werden.

Betonstahl

Betonstahl wird im EC 2-1-2 in Kapitel 3.2 erläutert. Der Eurocode legt in den Tabellen 3.2a und 3.2b die Parameter für die Spannungsdehnungsbeziehung fest. Dabei wird zwischen warmgewalzten und kaltverformten Betonstahl unterschieden.

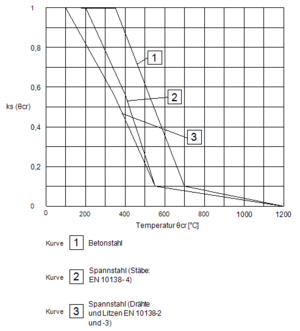
Bei einer Temperatur von rund 500°C erreichen die Festigkeitseigenschaften von Stahl kritische Werte. Im Eurocode ist diese als kritische Temperatur festgelegt. Um den Abfall der charakteristischen Festigkeit f_yk zu berücksichtigen, wird im EC 2-1-2 unter 4.2.4.3 der Beiwert k_s(θ) festgelegt, welcher von der Stahltemperatur abhängig ist.

Bemessungsverfahren im Stahlbetonbau nach EC 2-1-2

Für die Nachweise von Stahlbeton- und Spannbetonbauteilen, sieht der EC 2-1-2 drei verschiedene Nachweisebenen vor.:

1.Ebene: Tabellenverfahren

Von den zu untersuchenden Bauteilen werden die Querschnittsabmessungen mit Werten verglichen, welche zum Erreichen der vorgesehenen Feuerwiderstandsdauer nach Brandversuchen erforderlich sind.

2.Ebene: Vereinfachtes Rechenverfahren

Hier wird nachgewiesen, dass auch nach Ablauf der Feuerwiderstandsdauer eines Bauteils, alle maßgebenden Lasteinwirkungen aufgenommen werden können, ohne dass dieses versagt. Für die Beschreibung des Versagenszustandes im Brandfall und die Temperaturermittlung von Bauteilquerschnitten werden dabei Vereinfachungen getroffen.

3.Ebene: Allgemeines Rechenverfahren

Mit diesem Verfahren wird das tatsächlichen Tragvermögens für eine vorgegebene Feuerwiderstandsdauer ermittelt.

Die einzelnen Verfahren teilen sich in verschiedenen Varianten auf. Welches Verfahren angewendet werden muss, hängt von der geforderten Genauigkeit und den benötigten Aussagen ab. Der Nachweis mit tabellarischen Daten ist nicht immer Anwendbar. Gerade hier können die rechnerischen Verfahren große Vorteile bieten.

Tabellenverfahren

In der Abhängigkeit zur Feuerwiderstandsklasse werden für die Querschnittsabmessungen und Achsabstände der Bewehrung, Mindestwerte in Tabellen angegeben. Diese Tabellenwerte stammen aus Versuchsergebnissen und wurden durch theoretische Versuchsauswertungen und Erfahrungswerte bestätigt. In Ihnen sind Bemessungsergebnisse für Normbeanspruchungen von bis zu 240 Minuten enthalten.

Der Eurocode 2-1-2 enthält Bemessungstabellen für:

• Stützen mit Rechteck- oder Kreisquerschnitten bei ein- und mehrseitiger Brandbeanspruchung
• tragende und nicht tragende Wände.
• Balken mit Rechteck- und I-Querschnitt bei drei- oder vierseitiger Brandbeanspruchung.
• ein- oder zweiachsig gespannte Platten, Durchlaufplatten, Flachdecken und Rippendecken.

Hinweis : Die Tabellenwerte gelten für Normalbeton (2 000 bis 2 600 kg/m³, siehe EN 206-1) mit quarzhaltigen Zuschlägen. Die Querschnittsabmessungen für Balken und Platten dürfen um 10% verkleinert werden, wenn stattdessen kalksteinhaltige Zuschläge verwendet werden. Hinsichtlich der Schub- und Torsionstragfähigkeit und der Verankerung der Bewehrung, bedarf es bei Anwendung der Tabellen keiner weiteren Überprüfung. Hinsichtlich des Abplatzen von Beton bedarf es bei der Anwendung der Tabellenwerte, mit Ausnahme der Oberflächenbewehrung, keiner weiteren Überprüfung.

Die Anforderungskriterien (E) und (I) werden mit dem Einhalten der Mindestquerschnittabmessungen nach den Tabellen erfüllt. Wenn die tabellierten Mindestanforderungen eingehalten werden, gilt für die Tragfähigkeit (Kriterium R):

${{E}_{d,fi}}\leq {{R}_{d,fi}}$

Ed,fi...	Bemessungswert der Schnittgrößen im Brand
Rd,fi...	Bemessungswert der Tragfähigkeit (Widerstand) beim Brand

Die Tabellenwerte wurden unter der Annahme ermittelt, dass der Querschnitt unter Normaltemperatur voll ausgelastet ist. Sie gelten, sofern nicht anders angegeben, für einen Reduktionsfaktor η_fi von 0,7. Der Bemessungswert der Schnittgröße im Brandfall ergibt sich also mit: E_d,fi = 0,7*E_d = 0,7*R_d.

Die kritische Temperatur θ_cr für Betonstahl liegt unter diesen Umständen bei 500°C. Für diese ergibt sich der Ausnutzungsgrad k_s(θ_cr) zu 0,61. Die in den Tabellen angegebenen Mindestachsabstände der Zugbewehrung von Balken und Platten, sind für diese Temperatur festgelegt.

Für den Fall, dass ein Querschnitt nicht voll ausgelastet ist, darf der in den Bemessungstabellen angegebene Bewehrungsachsabstand a, auf Grundlage der kritischen Temperatur korrigiert werden. Dafür steht in der DIN EN 1992-1-2 das Bild 5.1 zur Verfügung. Mit diesem lässt sich die kritische Temperatur θ_cr in Abhängigkeit vom Ausnutzungsgrad k_s(θ_cr) bestimmen.

Bemessungskurven für die kritische Temperatur von Betonstahl und Spannstahl θ_cr nach Bild 5.1 der DIN EN 1992-1-2

Der Ausnutzungsgrad k_s(θ_cr) ergibt sich mit:

${{k}_{s}({\theta }_{cr})}={\frac {{\sigma }_{s,fi}}{{f}_{yk}{(20^{\circ }C)}}}$

σs,fi...	Stahlspannung unter Brandeinwirkung
fyk(20°C)...	charakteristischer Wert der Stahlfestigkeit bei einer Temperatur von 20°C (Normaltemperatur)

Die Stahlspannung unter Brandeinwirkung σ_s,fi ergibt sich mit:

${{\sigma }_{s,fi}}={\frac {{E}_{d,fi}}{{E}_{d}}}\cdot {\frac {{f}_{yk}{(20^{\circ }C)}}{{\gamma }_{s}}}\cdot {\frac {{A}_{s,prov}}{{A}_{s,req}}}$

Ed,fi...	Bemessungswert der Schnittgrößen im Brand
Ed...	Bemessungswert der zugehörigen Schnittgröße aus der Bemessung für Normaltenperatur nach DIN EN 1990
fyk(20°C)...	charakteristischer Wert der Stahlfestigkeit bei einer Temperatur von 20°C (Normaltemperatur)
γs...	Teilsicherheitsbeiwert der Bewehrung nach DIN EN 1992-1-1
As,req...	die erforderliche Bewehrungsfläche für den Grenzzustand der Tragfähigkeit nach DIN EN 1992-1-1
As,prov...	vorhandene Bewehrung

Anschließend kann mit dem Wert für k_s(θ_cr) aus dem Bild 5.1 die zugehörige kritische Temperatur θ_cr [°C] abgelesen werden.

Für den korrigierten Achsabstand der Bewehrung gilt:

${\triangle a}=0,1\cdot (500-{{\theta }_{cr}})[mm]$

Für die Bemessung von Stützen sind im EC 2-1-2 drei alternative Verfahren für die brandschutztechnische Bemessung enthalten. Die Methode A, die Methode B und Anhang C-

Methode A

Die Methode A enthält 2 Verfahren. Zum einen die Bemessung mit der EC 2-1-2 Tabelle 5.2a und als Alternative zu dieser die Gleichung 5.7 aus dem EC 2-1-2. Die Methode dient der technischen Brandschutzbemessung von überwiegend auf Druck beanspruchten, schlaff bewehrten und vorgespannten Betonstützen in Bauwerken, welche voll ausgesteift sind.

Hinweis : Damit sich die Ersatzlänge der Stütze im Brandfall halbiert, müssen die Stützenenden rotationsbehindert gelagert sein. Gemäß EC2-1-1 Abschnitt 5 gilt für die Ersatzlänge der Stütze im Brandfall $l_{0,fi}\leq 3m$ Im Brandfall gilt für die Lastausmitte nach Theorie 1. Ordnung $e=M_{0Ed,fi}/N_{0Ed,fi}\leq e_{max}$ Für die Bewehrung gilt $A_{s}<0,04\cdot A_{c}$

Bei der Bemessung von Druckgliedern spielt der Lastausnutzungsfaktor μ_fi eine große Rolle.

${{\mu }_{fi}}={\frac {{N}_{Ed,fi}}{{N}_{Rd}}}$

NEd,fi...	Bemessungswert für die Längskraft beim Brand
NRd...	Bemessungswert der Tragfähigkeit der Stütze bei Normaltemperatur

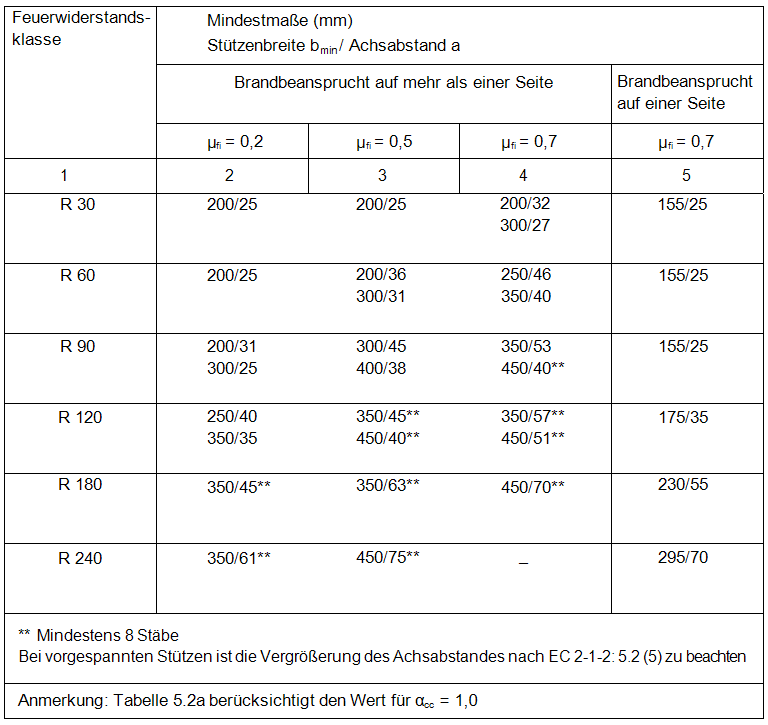
In der Tabelle 5.2a des EC 2-1-2 werden die Achsabstände und Mindestquerschnitte von Stützen in Abhängigkeit zu μ_fi dargestellt und der entsprechenden Feuerwiderstandsklasse zugeordnet. Grundlage der Tabelle sind Brandversuche, bei welchen eine zentrische und exzentrische Belastung unter Prüfungsbedingungen durchgeführt wurde.

Tabelle 5.2a für die Methode A, nach DIN EN 1992-1-2

Die Gleichung 5.7 des EC 2-1-2 dient als Alternative anstelle der Tabelle 5.2a und wurde aus Regressionsanalysen abgeleitet. Mit dieser Bemessungsgleichung wird, in Abhängigkeit zu den maßgebenden Einflussgrößen, die Feuerwiderstandsdauer R bestimmt.

$R=120\cdot {{\left({\frac {{{R}_{\eta fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120}}\right)}^{1,8}}$

Dabei ist:

${R_{\eta fi}}=83\cdot \left(1-{{\mu }_{fi}}\cdot {\frac {(1+\omega )}{(0,85/{{\alpha }_{cc}})+\omega }}\right)$	Einfluss des Lastniveaus
${R_{a}}=1,6\cdot (a-30)$	Einfluss des Achsabstandes
${R_{l}}=9,6\cdot (5-{{l}_{0,fi}})$	Einfluss der Stützenlänge
${R_{b}}=0,09\cdot b'$	Einfluss der Querschnittsabmessungen
${R_{n}}=0\quad f{\ddot {u}}r\quad n=4$	Einfluss der Bewehrung
${R_{n}}=12\quad f{\ddot {u}}r\quad n>4$

μfi...	dem Ausnutzungsgrad im Brandfall, siehe oben
ω...	dem mechanischer Bewehrungsgrad: $\omega ={\frac {{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}}$
αcc...	dem Abminderungsbeiwert der Betondruckfestigkeit zur Berücksichtigung der Langzeiteinwirkungen (siehe EN 1992-1-1)
a...	dem Achsabstand der Längsbewehrung, 25mm ≤ a ≤ 80mm
l0,fi...	der Ersatzstablänge im Brandfall, 2m ≤ l0,fi ≤ 6m
n...	der Anzahl der Bewehrungsstäbe
b´...	200mm ≤ b´ ≤ 450mm; Querschnittshöhe h ≤ 1,5*b
	= Ø Stütze für Kreisquerschnitte
	= 2Ac/(b+h) für Rechteckquerschnitte
b...	Querschnittsbreite

Der Nachweis ist erfüllt, wenn die tatsächliche Brandwiderstandsdauer mindestens der geforderten Brandwiderstandsdauer entspricht.

Hinweis : Die Gleichung 5.7 darf auch verwendet werden, wenn die Stützen nicht rotationsbehindert gelagert sind. für rechteckige Querschnitte beträgt die maximale Stützenlänge 6m und für runde Querschnitte 5m.

Damit ergibt sich für die Gleichung 5.7 der Vorteil, dass der allgemeine Anwendungsbereich größer ist, auch hinsichtlich der Mindestabmessungen.

Beispielrechnung

Brandschutznachweis Stahlbetonstütze (Bsp.)

Methode B und Anhang C

Die Methode B und die Bemessungstabellen des Anhangs C, welche eine Erweiterung der Methode B sind, ermöglichen unter anderem auch die Bemessung von Kragstützen. Allerdings liefern beide Verfahren nur sehr unsichere Ergebnisse und sind daher in Deutschland nicht zugelassen. Aus diesem Grund wird auf dieser Seite nicht weiter auf diese Verfahren eingegangen.

Vereinfachtes Verfahren

Als zweite Stufe bietet der EC 2-1-2 das vereinfachte Verfahren an. Dieses bietet mehr Anwendungsmöglichkeiten, als das zuvor beschriebene Tabellenverfahren. Grundlage des Verfahrens ist die Beschreibung der verringerten Tragfähigkeit von brandbeanspruchten Bauteilen, aufgrund von temperaturabhängigen Materialfestigkeiten und temperaturbedingten Verkleinerungen des Betonquerschnittes. Die Verkleinerung von Betonquerschnitten berücksichtigt die Zermürbung von Betonbereichen, welche einem Brand direkt ausgesetzt sind und keine tragenden Eigenschaften mehr aufweisen. Mit dem Restquerschnitt wird dann der Nachweis der Tragfähigkeit für Normaltemperatur nach DIN EN 1992-1-1 geführt, wobei die Abminderung der Materialfestigkeiten durch die temperaturabhängigen Reduktionsbeiwerte k_c(θ_M) und k_s(θ) berücksichtigt wird.

Im Anhang A des EC 2-1-2 wurden Diagramme mit Temperaturprofilen und Isothermen zusammengestellt. Diese können bei einer Beanspruchung nach ETK zur Ermittlung der Querschnittstemperaturen von Platten, Balken, Wänden und Stützen mit gewöhnlichen Querschnittsformen angewendet werden. Die Temperaturangaben dienen der Bestimmung der Bewehrungstemperaturen in Bauteilen, mit welchen dann die reduzierten Stahlfestigkeiten ermittelt werden können.

Varianten des vereinfachten Verfahrens

Das vereinfachte Verfahren besteht aus verschiedenen Berechnungsvarianten, welche in den informativen Anhängen des EC 2-1-2 erläutert werden.

• Anhang AA: Vereinfachtes Nachweisverfahren für Stahlbeton-Kragstützen im Brandfall
• Anhang B.1: 500 °C-Isothermen Methode
• Anhang B.2: Zonenmethode
• Anhang C: Knicken von Stützen unter Brandbedingungen
• Anhang D: Berechnungsmethode für Schub, Torsion und Verankerung der Bewehrung
• Anhang E: Vereinfachtes Rechenverfahren für Platten und Balken

Hinweis : Die Verfahren der Anhänge B.1, C und D sind für eine Anwendung in Deutschland nicht zugelassen, da die Ergebnisse dieser Methoden teils stark von denen des allgemeinen Verfahrens und anderer Methoden abweichen. Auf dieser Seite wird nicht weiter auf diese Methoden eingegangen

Zonenmethode

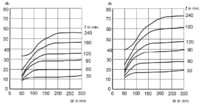Tabellen für die Ermittlung der Reduktionsbeiwerte az, aus der DIN EN 1992-1-2

Reduktion der Festigkeit und des Querschnittes, nach DIN EN 1992-1-2

Eine Methode des vereinfachten Verfahrens ist die Zonenmethode. Diese wird im EC 2-1-2 Anhang B.2 beschrieben. Die Methode eignet sich besonders für Bauteile, die zum einen bei Normaltemperatur nicht voll ausgelastet sind und zum anderen Querschnittsabmessungen oder Bewehrungsabstände haben, welche nicht die Mindestabmessungen der Bemessungstabellen aus Stufe 1 erreichen.

Die Zonenmethode besteht aus 4 Berechnungsschritten:

Schritt 1: Berechnung der temperaturabhängigen Verkleinerung des Betonquerschnittes

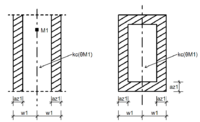
Der Querschnitt, der durch den Brand beschädigt wurde, wird durch einen reduzierten Querschnitt repräsentiert. Die Dicke dieser Zone wird durch das Maß a_z bezeichnet. Dieses wird mit Gleichungen oder Diagrammen ermittelt, welche im Anhang B.2 des EC 2-1-2 gegeben sind. Dabei steht der Wert w für die Hälfte der Querschnittsbreite.

Schritt 2: Ermittlung des Beiwertes k_c(θ_M)

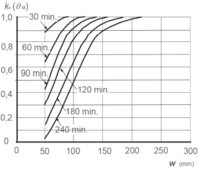Beiwert kc(θM) nach DIN EN 1992-1-2

Beiwert ks(θ) nach DIN EN 1992-1-2

Der Beiwert k_c(θ_M) gibt für die Druckzone des reduzierten Betonquerschnittes die temperaturbedingte reduzierte Druckfestigkeit an. Auch dieser Wert kann aus Gleichungen oder einem Diagramm des EC 2-1-2 Anhang B.2 entnommen werden. Die reduzierte Druckfestigkeit für den gesamten reduzierten Querschnitt wird dabei über den Punkt M bestimmt, welcher auf der Bauteilachse liegt.

Schritt 3: Ermittlung des Beiwertes k_s(θ)

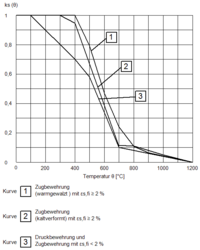
Die Bewehrungstemperatur wird mit den in Anhang A des EC 2-1-2 dargestellten Temperaturprofilen ermittelt. Die Reduktion der Stahlfestigkeit k_s(θ) ergibt sich in Abhängigkeit zur Bewehrungstemperatur nach dem Diagramm des Bildes 4.2a aus dem EC 2-1-2. Dieses wurde bereits unter mechanische Einwirkungen erläutert.

Schritt 4: Nachweis der Tragfähigkeit

Die Tragfähigkeit des Restquerschnittes R_fi,d,t wird dann analog zum Nachweis bei Normaltemperatur nach DIN EN 2-1-1 für die maßgebende Lasteinwirkung E_fi,d,t nach DIN EN 1-1-2 durchgeführt.

Hinweis : Bezüglich der Bemessung von Stützen wird die Anwendung ausdrücklich für Stützen mit kleinen Querschnitten empfohlen, Für eine brandschutztechnische Bemessung bei welcher eine Stützenverformung berücksichtigt werden muss, sind die Angaben des Anhang B.2 unzureichend. Die Anwendung der Zonenmethode für Druckglieder wird daher nach Anhang B.2 ausgeschlossen.

Verfahren nach Anhang E

Die Methode aus Anhang E darf für statisch bestimmt und und unbestimmt gelagerte biegebeanspruchte Bauteile verwendet werden, welche durch eine überwiegend gleichförmig verteilte Last belastet werden.
Die Bemessung für Normaltemperatur muss dabei mit Hilfe linear-elastischer Berechnung mit Momentenumlagerung nach DIN EN 1991-1-2 kleiner 15% erfolgt sein. Wenn die Auflager gegenüber der Feuerwiderstandsdauer eine ausreichende Rotationsfähigkeit aufweisen, ist dieses Verfahren auch für eine Momentenumlagerung größer 15% anwendbar.
Allgemein ist dieses Verfahren als eine Erweiterung des Tabellenverfahrens zu verstehen. Die Biegetragfähigkeit kann auch bestimmt werden, wenn der Feldbewehrungsabstand a kleiner als der Tabellenwert des Tabellenverfahrens ist. Die Mindestquerschnittabmessungen aus den Tabellen 5.5 bis 5.11 des EC 2-1-2 sollten nicht unterschritten werden.

Um das aufnehmbare Feldmoment für den Brandfall zu bestimmen, ist die Ermittlung der Festigkeitsabnahme der unten liegenden Biegezugbewehrung erforderlich.

Für den allgemeinen Nachweis gilt:

${{M}_{Ed,fi}}$ ≤ ${{M}_{Rd,fi}}$

MEd,fi...	maximales Bemessungsmoment im Brandfall
MRd,fi...	aufnehmbares Bemessungsmoment im Brandfall

Das aufnehmbare Bemessungsmoment M_Rd,fi ergibt sich für statisch bestimmt gelagerte Platten und Balken aus:

${{M}_{Rd,fi}}={\frac {{\gamma }_{s}}{{\gamma }_{s,fi}}}\cdot {{k}_{s}(\theta )}\cdot {{M}_{Ed}}\cdot {\frac {{A}_{s,prov}}{{A}_{s,req}}}$

γs...	Teilsicherheitsbeiwert für Stahl nach DIN EN 1992-1-1
γs,fi...	Teilsicherheitsbeiwert für Stahl im Brandfall
ks(θ)...	Reduktionsfaktor für die Stahlfestigkeit für die vorhandene Temperatur θ zur vorhandenen Feuerwiderstandsdauer. θ darf dabei für den gewählten Achsabstand aus Anhang A genommen werden
MEd...	maßgebendes Moment für die Bemessung bei Normaltemperatur nach DIN EN 1992-1-1
As,prov...	vorhandene Fläche der Bewehrung
As,req...	erforderliche Fläche der Zugbewehrung aus der Bemessung bei Normaltemperatur nach DIN EN 1992-1-1

Dazu gilt:

${\frac {{A}_{s,prov}}{{A}_{s,req}}}$ ≤ $1,3$

Für durchlaufende Platten und Balken ergibt sich das aufnehmbare Bemessungsmoment M_Rd,fi aus:

${{M}_{Rd,fi}}={\frac {{\gamma }_{s}}{{\gamma }_{s,fi}}}\cdot {{M}_{Ed}}\cdot {\frac {{A}_{s,prov}}{{A}_{s,req}}}\cdot {\frac {{d}-{a}}{d}}$

a...	der erforderliche mittlere Achsabstand aus Tabelle 5.5, Spalte 5 für Balken und Tabelle 5.8, Spalte 3 für Platten
b...	statische Nutzhöhe des Querschnitts

Brandschutztechnische Bemessung von Kragstützen

Für die Bemessung von Kragstützen dürfen die Tabellen aus 5.2a des Tabellenverfahrens nicht verwendet werden, da diese nur für Stützen in ausgesteiften Gebäuden mit rotationsbehinderter Lagerung geeignet sind. Auch die Gleichung aus 5.7 darf nicht verwendet werden. Da ansonsten nur das sehr aufwendige allgemeine Verfahren bleibt, wurde speziell für Stahlbeton-Kragstützen ein vereinfachtes Verfahren erarbeitet und als Anhang AA im nationalen Anhang des EC 2-1-2 übernommen.

Das Verfahren stellt für 4 Standardfälle die Traglasten N_R,fi,d,90 und Gesamtmomente M_tot,fi,d,90 in Standarddiagrammen dar. Das Verfahren gilt für eine ETK-Beanspruchung von 90 Minuten.

Ablaufdiagramm zum Nachweis der Tragfähigkeit einer Stahlbeton-Kragstütze für die Feuerwiderstandsklasse R90

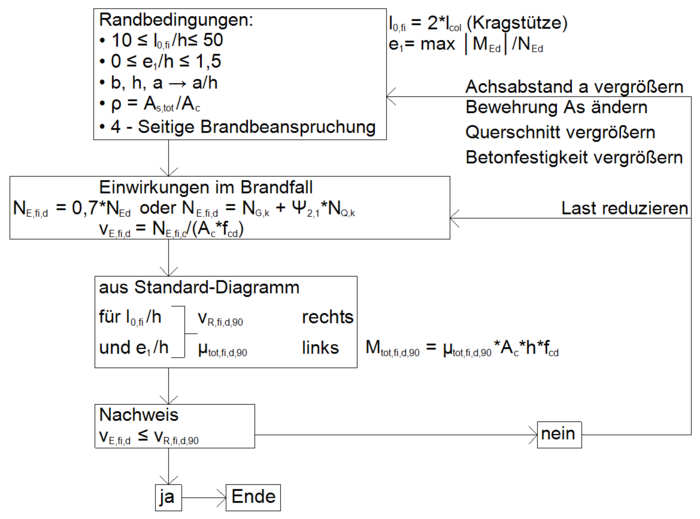
Die 4 Standarddiagramme gelten für:

• eine vierseitige Beanspruchung
• die Querschnittsabmessungen h=300mm, h=450mm, h=600mm und h=800mm
• einlagige Bewehrung aus Betonstahl B500, bei einem bezogenen Achsabstand der Längsbewehrung a/h = 0,10 und einem geometrischen Bewehrungsverhältnis ρ = 2%
• Normalbeton der Festigkeitsklasse C30/37 mit überwiegend quarzhaltiger Gesteinskörnung, einer Rohdichte von ρ = 2400 kg/m3 und einer Betonfeuchte von k = 3% (Massenanteile)

In den Standarddiagrammen werden die Bemessungswerte für das bezogene Einspannmoment am Stützenfuß μ_tot,fi,d,90 und die bezogene Stützentraglast ν_R,fi,d,90, für den Grenzzustand der Tragfähigkeit, als Scherparameter in Abhängigkeit zu der bezogenen Knicklänge 10 ≤ l_0,fi/h ≤ 50 und in Abhängigkeit zu der bezogenen Lastausmitte e₁/h ≤ 1,5 dargestellt.

Bei Abweichungen der Brandbeanspruchung und für abweichende statisch-konstruktive Randbedingungen, stehen Faktoren zur Verfügung. Mit diesen können die Werte µ_tot,fi,d,90 und ν_R,fi,d,90 der Standarddiagramme modifiziert und angewendet werden.

${{\mu }_{tot,fi,d,90}}={{k}_{fi}}\cdot {{k}_{u}}\cdot {{k}_{C}}\cdot {{k}_{\rho }}\cdot {{X}_{tot,90}}$

${{\nu }_{R,fi,d,90}}={{k}_{fi}}\cdot {{k}_{u}}\cdot {{k}_{C}}\cdot {{k}_{\rho }}\cdot {{X}_{R90}}$

μtot,fi,d,90...	Bemessungswert des bezogenen Einspannmomentes am Stützenfuß
νR,fi,d,90...	Bemessungswert der bezogenen Stützlast
kfi...	Faktor zur Berücksichtigung der Brandbeanspruchung (1- oder 3-seitig)
ka...	Faktor zur Berücksichtigung des Achsabstandes (0,05 ≤ a/h ≤ 0,15)
kC...	Faktor zur Berücksichtigung der Betonfestigkeitsklasse (C 20/25 bis C 50/60)
kρ...	Faktor zur Berücksichtigung der Bewehrungsverhältnisse (1 % ≤ ρ ≤ 8 %)
Xtot,90...	µtot,fi,d,90 aus den Standard-Diagrammen
XR90...	νR,fi,d,90 aus den Standard Diagrammen

Hinweis : Die Ersatzlänge l0,fi von Kragstützen für den Brandfall, ergibt sich durch 2*l. Dabei bezeichnet l die Stützenlänge zwischen den Einspannstellen.

Beispielberechnung

Vereinfachtes Verfahren nach nationalen Anhang AA, Stahlbetonstütze im Brandfall, 4-seitige Brandbeanspruchung (Bsp.)

Allgemeines Verfahren

Mit dem allgemeinen Rechenverfahren kann für brandbeanspruchte Einzelbauteile, Teil- und Gesamttragwerke, dass Trag- und Verformungsverhalten nummerisch Simuliert werden. Dies ist bei einer beliebigen Querschnittsform unter voller, aber auch lokaler Temperaturbeanspruchung möglich. Mit dem Verfahren soll eine wirkungsnahe Berechnung brandbeanspruchter Tragwerke ermöglicht werden. Im Vergleich zum tabellarischen Nachweis und zum vereinfachten Rechenverfahren, erfordert das allgemeine Rechenverfahren den größten Aufwand.

Es besteht aus einer thermischen Analyse in welcher die Querschnittserwärmung infolge der äußeren Temperatureinwirkung berechnet wird und einer mechanischen Analyse, welche das Trag- und Verformungsverhalten des Bauteils oder Tragwerks für die vorhandenen äußeren Belastungen im Brandfall untersucht. Diese beiden Schritte dürfen auch getrennt voneinander durchgeführt werden.

In der DIN EN 1991-1-2 und dem zugehörigen nationalen Anhang, werden die Rechengrundlagen zur Ermittlung der Temperatur- und Lasteinwirkung genormt (siehe Seite Heißbemessung). Des Weiteren werden Angaben über die temperaturabhängige Veränderung der thermo-mechanischen Baustoffeigenschaften nach der DIN EC 2-1-2 benötigt.

Insbesondere für eine statisch unbestimmte Konstruktion, bei denen das Verhalten des Gesamtsystems nicht durch Versuche am Teilsystem bestimmt werden kann, ist die numerische Modellierung und rechnerische Nachweisführung praktisch die einzige Möglichkeit, um die Feuerwiderstandsdauer des Tragwerks zu bestimmen.

Sowohl die thermische, als auch die mechanische Analyse sind numerisch sehr aufwändig. Daher können Sie nur programmgesteuert erfolgen. Die Rechenprogramme für das allgemeine Verfahren müssen validiert sein. Im Anhang CC der DIN EN 1991-1-2 NA wurden dafür Validierungsbeispiele mit zulässigen Ergebnistoleranzen erstellt, mit denen die Anwendbarkeit von Rechenprogrammen für das allgemeine Verfahren überprüft werden kann.
In Deutschland bedarf es für die Anwendung des allgemeinen Rechenverfahrens einer Abstimmung mit der Bauaufsichtsbehörde. Für derartige Brandschutznachweise ist eine Prüfung der Berechnung durch einen Prüfingenieur oder Prüfsachverständigen erforderlich.

thermische Analyse

Mit der thermischen Analyse wird, ausgehend von der Heißgastemperatur im Brandraum, die Entwicklung und Verteilung der Temperatur in Bauteilen berechnet. Die Materialkennwerte des Bauteilquerschnittes, sowie eventuell vorhandene Schutzschichten, müssen dabei berücksichtigt werden.

Die Ermittlung der thermischen Einwirkungen auf Bauteile erfolgt dabei mit dem zeitlichen Verlauf der Heißgastemperatur, welche nach der DIN EN 1991-1-2 ermittelt wurde. Die Grundlage für die Temperaturverteilung innerhalb von Bauteilen ist die Differenzialgleichung von Fourier. Sie beschreibt die instationäre Wärmeleitung in Festkörpern unter der Voraussetzung, dass sich in diesen keine Wärmequelle oder Senke befindet.

${\frac {\delta \theta }{\delta t}}=a\cdot ({\frac {\delta ^{2}\theta }{\delta x^{2}}}+{\frac {\delta ^{2}\theta }{\delta y^{2}}}+{\frac {\delta ^{2}\theta }{\delta z^{2}}})$

θ...	Temperatur [K]
t...	Zeit [s]
x, y, z...	Raumkoordniaten
a...	Temperaturleitzahl [m2/s]

Dabei ergibt sich die Temperaturleitzahl a zu:

${a}={\frac {\lambda }{\rho \cdot {{c}_{\rho }}}}$

λ...	Wärmeleitfähigkeit
ρ...	Rohdichte
cρ...	spezifische Wärme [J/(kgK)]

Hinweis : Eine analytische Lösung der Differentialgleichung ist nur in einem homogenen und isotropen Körper, mit temperaturunabhängigen Materialeigenschaften und eindimensionalem Wärmestrom möglich.

Die temperaturabhängigen Materialeigenschaften λ, c_p und ρ, müssen für die Berechnung der Temperaturverteilung innerhalb brandbeanspruchter Bauteile berücksichtigt werden. Die Verteilung der Bauteiltemperatur ist somit von temperaturabhängigen Eingangsparametern abhängig. Die Lösung ist mit nummerischen Methoden wie der Finite-Elemente-Methode oder der Finite-Differenzen-Methode möglich.

Folgende Vereinfachungen dürfen für Baupraktische Fälle getroffen werden:

• Wasserdampfbewegungen müssen nicht erfasst werden. Durch die spezifische Wärmekapazität werden alle Energie verzehrenden Vorgänge berücksichtigt.
• Die Bewehrung darf bei praxisüblichem Bewehrungsgehalt bei der thermischen Analyse vernachlässigt werden. Es wird davon ausgegangen, dass die Temperatur in der Achse des Bewehrungsstabes ungefähr der Temperatur der ungestörten Bewehrung entspricht.
• In Bauteillängsrichtung darf die Temperaturausbreitung vernachlässigt werden.

mechanische Analyse

Die mechanische Analyse untersucht das Trag- und Verformungsverhalten brandbeanspruchter Bauteile und Tragwerke. Das Berechnungsziel ist zum einen die maßgebende mechanische Einwirkung unter Brandbeanspruchung E_fi,d,t und zum anderen die Tragfähigkeit für den Brandfall R_fi,d,t.

Die Einwirkungsseite berücksichtigt zum einen die behinderten thermischen Verformungen welche Zwangskräfte und Momente erzeugen, außerdem die mechanischen Einwirkungen und wenn vorhanden, die nichtlinearen geometrischen Einflüsse aus der Berechnung nach Theorie II. Ordnung. Die mechanischen Einwirkungen werden für eine außergewöhnliche Bemessungssituation oder vereinfacht mit dem Reduktionsfaktor für die Einwirkung bei Normaltemperatur angenommen.

Die Widerstandsseite berücksichtigt die thermischen Dehnungen und die thermo-mechanischen Eigenschaften (Spannungs-Dehnungsbeziehungen) der Baustoffe. Damit die Gleichgewichts- und Verformungsbedingungen erfüllt sind, werden die Querschnittsdehnungen ermittelt. Diese setzen sich zusammen aus den thermischen Dehnungen und den spannungserzeugenden Dehnungen der Baustoffe. Die zur Erfüllung der Verträglichkeits- und Gleichgewichtsbedingungen notwendige Dehnungsverteilung, muss dann iterativ bestimmt werden.

Nebenwirkungen durch Brandbeanspruchung

Betonabplatzungen

Bei Betonbauteilen kann eine schnelle Erwärmung und eine hohe Temperaturbeanspruchung zu explosionsartigen Abplatzungen führen. Diese sind schon in der frühen Phase des Brandes möglich. Nach dem EC 2-1-2 Kapitel 4.5.1 müssen diese Betonabplatzungen vermieden oder zumindest ihr Einfluss auf die Leistungsanforderungen (R, I, E) berücksichtigt werden, da diese erhebliche Schäden verursachen können.

Eine Ursache für Betonabplatzungen sind thermohydraulische Prozesse. Das im Beton enthaltene Wasser wird durch die Temperaturerhöhung in Wasserdampf umgewandelt, wodurch sich das Volumen um etwa das 1700-fache vergrößert. Wenn dieses zusätzliche Volumen nicht über das Porensystem nach außen abgeführt wird, entsteht ein sehr großer innerer Druck. Dieser übersteigt schnell die Betonzugfestigkeit, woraufhin es zu explosionsartigen Abplatzungen kommt.

Eine weitere Ursache sind thermomechanische Prozesse. Durch die nicht lineare Temperaturverteilung im Betonquerschnitt, dehnen sich die Betonkomponenten unterschiedlich aus. Daraus resultieren innere Spannungen, welche Abplatzungen zur Folge haben können.

Das allgemeine Abplatzverhalten wird durch viele Faktoren beeinflusst. Zu diesen gehören unter anderem die Betonfestigkeit, der Wassergehalt, die Temperaturbeanspruchung, die Bauteilgeometrie, die mechanische Beanspruchung, die Temperaturverteilung im Querschnitt, sowie der Art des Zuschlagstoffes.

Für einen Feuchtegehalt von 4% gilt nach EC 2-1-2, dass Betonabplatzungen unwahrscheinlich sind. Üblicherweise wird dieser im Hochbau nicht überschritten. Sollte der Feuchtegehalt dennoch höher liegen, können die Abplatzungen abgeschätzt werden. Dazu nimmt man den Verlust an Betondeckung als Bewehrungsstab im Querschnitt an und berechnet dann die reduzierte Tragfähigkeit.

Wird hingegen hochfester Beton verwendet, müssen weitere Maßnahmen getroffen werden. Diese werden im EC 2-1-2 Abschnitt 6.2 erläutert.

Einfluss der Dehnungen auf das statische System

Die temperaturabhängigen Dehnungen des Betons und des Stahls können ungünstige Verformungen und Zwängungen verursachen, welche besonders berücksichtigt werden müssen. Durch den Zuwachs der Verformung reduziert sich die Tragfähigkeit. Aus der drastischen Abnahme der E-Module von Beton und Stahl lässt sich schließen, dass der Einfluss der Verformung auf die Schnittgrößen nach Theorie II. Ordnung im Brandfall stark zunimmt. Dies betrifft Stützen und verschiebliche Bauteile.

Einspannung von Pendelstützen im Brandfall

Stützen werden bei einem Brand in einem ausgesteiften Gebäude größtenteils durch eine horizontale Verschiebung des Stützenkopfes beansprucht. Die Verdrehung an den Enden der Stütze, kann hingegen vernachlässigt werden. Durch die Verformung, welche im Brandfall entsteht, ergibt sich die Ersatzlänge der Stütze für den Brandfall:

• in innenliegende Geschossen mit: ${{l}_{0,fi}}=0,5\cdot {l}$
• am Rand und im obersten Geschoss mit: $0,5\cdot l\leq {{l}_{0,fi}}\leq 0,7\cdot {l}$

l...	Stützenlänge zwischen den Einspannstellen

Die Enden von Stützen müssen rotationsbehindert gelagert werden, damit die Verdrehung am Kopf- und Fußpunkt vernachlässigt werden kann. Bei Stützen in Stahlbetontragwerken ist dies in der Regel erfüllt, wenn diese mit einer Ersatzlänge l₀ = 1 für Normaltemperatur bemessen werden und die Stützenenden mit einer konstruktiven Anschlussbewehrung versehen werden.

Berechnung von Stahlbetonbauteilen mit Softwarelösungen

Die plausible Eingabe der Parameter in die Berechnungsprogramme, ist bei der Bemessung von Stahlbetonbauteilen entscheidend für das Ergebnis. Insbesondere bei der Heißbemessung haben kleine Änderungen große Auswirkungen auf beispielsweise die erforderliche Bewehrung.
Bei Stahlbetonstützen ist aufgrund des statischen Systems, die Empfindlichkeit auf Ausmitten und Steifigkeiten generell sehr hoch. Bei der Heißbemessung von Stahlbetonstützen verstärkt sich der Effekt noch weiter. Durch die Reduzierung der Steifigkeiten und Druck- bzw. Zugfestigkeiten von Beton und Stahl, ergeben sich bei der Berechnung mittels Theorie II. Ordnung nochmal größere Verformungen. Diese erzeugen wiederum größere Schnittkräfte, welche von dem Material aufgenommen werden müssen. Nun hat zum Beispiel der Stahl in einer Stütze nicht überall die gleiche Temperatur und somit auch nicht die dieselbe Tragfähigkeit. Insofern ist die Anordnung der Bewehrung entscheidend für das Ergebnis der Berechnung. Doch insbesondere hier bieten Softwarelösungen meistens viele Varianten der Bewehrungsanordnung, welche genau betrachtet werden müssen, um wirtschaftliche Ergebnisse zu erzielen.
Drei Einstellungsmöglichkeiten sollten bei einer Heißbemessung von Stahlbetonstützen immer überprüft werden:

Betondeckung

Die Betondeckung ist die Schutzschicht für den Bewehrungsstahl. Je höher die Betondeckung ist, desto geringer ist die Temperatur im Stahl. Somit gewinnt das Material an Tragfähigkeit. Die Erhöhung der Betondeckung verschiebt die Bewehrung also in das Innere der Stütze, wodurch die Temperatur stark abnimmt. Das kann schon bei geringen Veränderungen große Auswirkungen haben, da der Anstieg der Temperatur am Stützenrand extrem steil ist.

Bewehrungswahl

• Bewehrung über den Umfang verteilen
• zusätzliche Bewehrung manuell mittig zum Randbereich der Stütze einlegen
• Die Bewehrung mehr in der Mitte der Stütze konzentrieren

Durch die starke Reduzierung der Lasten kann das Knicken in beide Richtungen maßgebend werden, sodass die eingelegte Eckbewehrung oder die einseitige Bewehrung, die Belastung nicht mehr aufnehmen kann. Außerdem nimmt die Temperatur zur Mitte der Stütze hin ab und die Festigkeit des Betonstahls wird weniger reduziert. Somit werden Bewehrungswahlen, die für die kalte Bemessung hilfreich sind, für die Heißbemessung ungünstig. Auf der sicheren Seite für die Heißbemessung ist immer eine umfangverteilte Bewehrung mit möglichst mittig liegenden Eisen.

Statisches System

Eine Stütze verändert unter Brandbeanspruchung zum Teil ihr statisches System. Zum einen lässt die Einspannung bei Pendelstützen eine Reduzierung der Knicklänge um 50% zu. Zum anderen ist zu untersuchen, ob bei Kragstützen eine teilweise Einspannung am Stützenkopf möglich ist, beispielsweise durch Stahlbetonbinder bei großen Hallensystemen. Diese Erleichterungen können bei der Bemessung auf jeden Fall berücksichtigt werden, müssen aber meistens manuell bei der Software ausgewählt bzw. angegeben werden.

Quellenangaben

Seiteninfo Status: Seite fertig, ungeprüft