Verankerungslänge
Die Verankerungslänge bezeichnet die Verlängerung von Bewehrungsstäben über ihre rechnerische Notwendigkeit hinaus, um die am Stabende noch vorhandene Randzugkraft in den Beton einzuleiten. Die Bestimmung der Verankerungslänge gehört zu den nötigen Nachweisen eines Bauteils und gliedert sich in die konstruktive Durchteilung ein.
Zu erstellen:
- Seite Verankerungslänge
- Bsp Endauflager
- Bsp Zwischenauflager
- Bsp Außerhalb vom Auflager
- Bsp Konsole
- Bsp Einzelfundament
- Bsp Kragarmende
Allgemeine Informationen
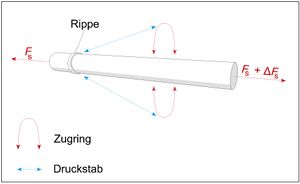
Verbund zwischen Beton und Stahl
Die Übertragung von Kräften zwischen Beton und Bewehrungsstahl erfolgt über den Verbund zwischen beiden Materialien.
Theoretischer Hintergrund der Verankerungslänge
Formen und Beiwerte der Verankerungslänge
Grundwert der Verankerungslänge
Der Grundwert der Verankerungslänge ist abhängig von drei Größen: dem Stabdurchmesser Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \O_s} , der Stahlspannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd}} und der Verbundfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{bd}} . Für eine kurze Verankerungslänge sorgen kleine Stabdurchmesser, eine geringe Stahlspannung und hohe Verbundfestigkeit. Die Formel zur Bestimmung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd}} lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd} = \frac{\O_s}{4} \cdot \frac{{\sigma}_{sd}}{f_{bd}}}
Bemessungswert der Verankerungslänge
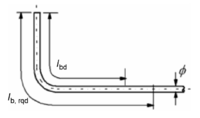
Der Bemessungswert der Verankerungslänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd}} misst die Länge vom Beginn der Verankerungslänge bis zum Stabende. Die Formel hierfür ist
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd} = {\alpha}_1 \cdot {\alpha}_3 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
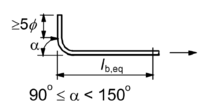
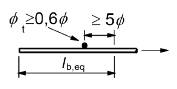
Ersatzverankerungslänge
Alternativ zur Bestimmung der tatsächlichen, gegebenenfalls gebogenen Verankerungslänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd}} kann vereinfacht die gerade Stablänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq}} ermittelt werden. Die Formel hierfür lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot l_{b,rqd}}
Die Ermittlung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq}}
ist üblich für die Mehrzahl der Fälle der Ermittlung der Verankerungslänge. Lediglich dort, wo die Verankerungslänge unmittelbar an der Stelle der Biegung beginnt, wird auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd}}
zurückgegriffen.
Beiwerte der Verankerungslänge
Bei der Ermittlung des Bemessungswerts der Verankerungslänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd}} oder der Ersatzverankerungslänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq}} aus dem Grundwert der Verankerungslänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd}} kommen einige Beiwerte zum Einsatz. Diese sind wie folgt:
| Beiwert | Bedeutung |
|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1} | - Beiwert für Formgebung |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_2} | - Beiwert für Mindestbetondeckung |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_3} | - Beiwert für nicht angeschweißte Querbewehrung |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_4} | - Beiwert für angeschweißte Querbewehrung |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5} | - Beiwert für Querdruck |
Übersicht über die Beiwerte
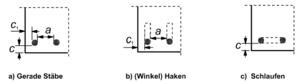
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha_1}}
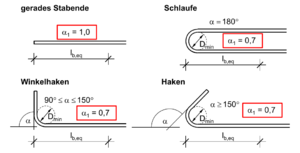
- Formgebung:
Bei bestimmten Stabenden gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 0,7} , da die Zugkraft durch das Aufbiegen auf einer kürzeren horizontalen Länge abgetragen werden kann. Die an der Krümmung entstehenden Spaltzugkräfte müssen durch hinreichende Betondeckung und Stababstände kompensiert werden, hier ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_d > 3 \O_s} festgelegt. Alternativ können die Spaltzugkräfte auch durch Querdruck oder enge Verbügelung im Verankerungsbereich (Bügelabstand < 50 mm) aufgenommen werden.
Bei der Verwendung von Schlaufen besteht zusätzlich die Möglichkeit, unter Einhalten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_d > 3 \O_s} und eines Biegerollendurchmessers Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D \geq 15 \O_s} , den Beiwert auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_1 = 0,5} zu reduzieren.
Druckstäbe sind immer mit geradem Stabende zu verankern.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha_2}} - Mindestbetondeckung:
Der Beiwert für die Mindestbetondeckung erlaubt theoretisch eine Reduzierung auf
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_2 = max\left\{ {\begin{matrix} 1 - \frac{0,15 \cdot (c_d - \O_s)}{\O_s} \\ 0,7 \end{matrix}} \right\} \leq 1,0}
In Deutschland ist dieser Beiwert aus der Formel zur Ermittlung des Bemessungswerts der Verankerungslänge gestrichen. Der Grund hierfür liegt in den möglichen Versagensfällen bei ungenügender Verankerungslänge. Diese sind das Herausziehen des Stabes und die Bildung von Spaltrissen im Beton. Eine hinreichende Betondeckung und ein genügender Stababstand erhöhen die Sicherheit gegen Spaltrisse, aber nicht gegen das Herausziehen. Somit würde der Beiwert eine Sicherheit vermitteln, die er gar nicht erzeugt.
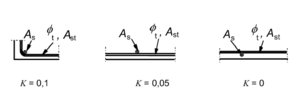
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha_3}} - Nicht angeschweißte Querbewehrung:
Der Beiwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_3}
betrachtet den günstigen Einfluss einer nicht angeschweißten Querbewehrung im Verankerungsbereich. Dieser gilt allerdings nur, wenn die verwendete Querbewehrungsmenge die Mindestquerbewehrungsmenge übersteigt. Bestimmt wird der Beiwert mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_3 = max\left\{ {\begin{matrix} 1 - K \cdot \lambda \\ 0,7 \end{matrix}} \right\} \leq 1,0}
Dabei ist
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = (\sum A_{st} - \sum A_{st,min}) / A_s} |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum A_{st}} | die Querschnittsfläche der Querbewehrung innerhalb der Verankerungslänge |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum A_{st,min})} | die Querschnittsfläche der Mindestbewehrung |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_s} | die Querschnittsfläche des größten einzelnen verankerten Stabs |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K} | Beiwert entsprechend des Bildes |
Für Druckstäbe gilt generell Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_3 = 1,0}
.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha_4}} - Angeschweißte Querstäbe:
Unter bestimmten Vorgaben kann einer oder mehrere angeschweißte Querstäbe die benötigte Verankerungslänge reduzieren. Werden die angegebenen Bedingungen eingehalten, so gilt sowohl für Zug- als auch für Druckstäbe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_4 = 0,7} .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha_5}} - Querdruck:
Der Beiwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_5} betrachtet den Einfluss von Querdruck oder -zug im Verankerungsbereich. Unter Annahme eines Querdrucks Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} senkrecht zur Verankerungsebene berechnet sich der Beiwert als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_5 = max\left\{ {\begin{matrix} 1 - 0,04 \cdot p \\ 0,7 \end{matrix}} \right\}}
Für bestimmte Situationen gibt es festgelegte Werte für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_5} :
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,5} | - bei Querzug senkrecht zur Verankerungsebene |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2/3} | - bei direkter Lagerung |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2/3} | - bei einer allseitig durch Bewehrung gesicherten Betondeckung von mindestens Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10 \cdot \O_s} |
Mindestverankerungslänge
Für Zugstäbe ist die Mindestverankerungslänge definiert als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Für Druckstäbe gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,6 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }
Am Zwischenauflager gilt in Deutschland vereinfachend
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = 6 \cdot \O_s}
Randzugkraft
Ansätze der Berechnung der Verankerungslänge
Situationen der Verankerungslänge
Die verschiedenen Situationen der Verankerungslänge unterscheiden sich vor allem in der Ermittlung der erforderlichen Bewehrungsmenge an der jeweiligen Stelle. Darüber hinaus gelten gegebenenfalls besondere Regeln für die Bestimmung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{bd}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min}} .
Verankerung am Endauflager
Am Endauflager wird die zu verankernde Zugkraft maßgeblich durch die einwirkende Querkraft bestimmt. Die Formel zur Berechnung lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{sd} = V_{Ed} \cdot \frac{a_L}{z} + N_{Ed} \geq \frac{V_{Ed}}{2}}
Am Endauflager kann vereinfachend Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed} = Auflagerkraft} angesetzt werden. Aus der Randzugkraft wird die benötigte Bewehrung berechnet werden als
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = \frac{F_{sd}}{f_{yd}}}
Die Verankerungslänge am Endauflager beginnt an der Auflagerkante. Die Verankerung muss mindestens bis zur rechnerischen Auflagerlinie des statischen Systems reichen. Außerdem müssen mindestens 25 % der Feldbewehrung bis ins Auflager geführt und dort verankert werden.
Berechnungsbeispiel zur Verankerung am Endauflager
Verankerung am Zwischenauflager
Die am Zwischenauflager endende Feldbewehrung liegt im Druckbereich. Deshalb ist sie in vielen Fällen rechnerisch nicht nötig, es gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf} = 0} , gleiches gilt damit auch für und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,rqd}} . Aus diesem Grund ist am Zwischenauflager Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min}} maßgeblich, die außerdem auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = 6 \cdot \O_s} reduziert wird. Die Verankerungslänge am Zwischenauflager beginnt an der Auflagerkante.
Berechnungsbeispiel zur Verankerung am Zwischenauflager
Verankerung außerhalb von Auflagern
Abseits der Auflager eines Balkens enden Bewehrungsstäbe im Kontext der Zugkraftdeckung. Bei dieser sind erforderliche und vorhandene Bewehrung an der jeweiligen Stelle unmittelbar bekannt. Damit kann die Bestimmung der Verankerungslänge ohne besondere Regeln durchgeführt werden.
Berechnungsbeispiel zur Verankerung außerhalb von Auflagern
Verankerung am Kragarmende
Für die Verankerungslänge am Kragarmende gibt es keine expliziten Berechnungsvorschriften. Sie wird in der Regel nicht nachgewiesen
Berechnungsbeispiel zur Verankerung am Kragarmende
Verankerung am Rand von Einzelfundamenten
Berechnungsbeispiel zur Verankerung am Rand von Einzelfundamenten
Verankerung an Konsolen
Die Zugkräfte in Konsolen werden generell über eine bis drei Schlaufen aufgenommen. Die Verankerung dieser Zugbewehrung unter der Last in Konsolen gleicht dem Ablauf am Endauflager, da sich die beiden Situationen ähneln. Bei der Bemessung von Konsolen wird die benötigte Bewehrungsmenge unmittelbar an der zu verankernden Stelle bestimmt, damit ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,erf}} bekannt. Zu beachten ist, dass die Verankerungslänge an Konsolen an der der Stütze zugewandten Seite beginnt.