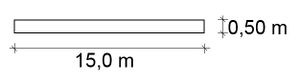
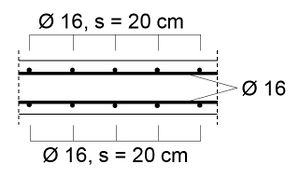
Zwang - verringerte Zwangsbeanspruchung in einer Sohlplatte (Bsp.)
Beispiel 1 - Mindestbewehrung zur Begrenzung der Rissbreite in einer Sohlplatte für eine verringerte Zwangsbeanspruchung
Aufgabenstellung
Als Vergleich soll für die Sohlplatte aus dem Beispiel "Zwang - Mindestbewehrung zur Rissbreitenbegrenzung für eine Sohlplatte (Bsp.)" die verringerte Zwangsbeanspruchung und die zugehörige Mindestbewehrung ermittelt werden.
Diese Ermittlung der verminderten Zwangsbeanspruchung gilt als Ergänzung zur DIN EN 1992-1-1[N 1] und wird im "Lohmeyer Stahlbetonbau" [F 1] empfohlen.
Diese Empfehlung darf nur für eine Beanspruchung aus dem Abfließen der Hydratationswärme angewendet werden, wenn ein späterer Zwang mit Sicherheit ausgeschlossen werden kann.
Im Anschluss an diese Berechnung wird ein Vergleich mit dem Beispiel "Zwang - Mindestbewehrung zur Rissbreitenbegrenzung für eine Sohlplatte (Bsp.)" durchgeführt.
Vorgaben
Sohlplattenabmessungen L / B / h: 17,00 / 15,00 / 0,50 m Expositionsklasse: XC2 - Gründungsbauteil Betonfestigkeitsklasse: C35/45 Betonzugfestigkeit: fctm = 3,2 N/mm2 Bewehrung aus der Statik: ø 16, s = 20 cm as,o = as,u = 10,05 cm2/m Betondeckung: cv = cnom = 20 + 15 + 20 = 55 mm Unterkonstruktion: Unterbeton mit Flügelglättung und 2 Lagen PE-Folie
Eine Beanspruchung aus spätem Zwang kann ausgeschlossen werden.
Es ist eine zentrische Zwangsbeanspruchung aus dem Abfließen der Hydratationswärme maßgebend.
Lösung
Ermittlung der zulässigen Rissbreite
Die Sohlplatte besteht aus Stahlbeton und es ist die Expositionsklasse XC2 vorgegeben.
Somit beträgt die zulässige Rissbreite
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w_k = \underline{0,3mm} } .
| 1 | 2 | 3 | 4 | 5 | |
| Expositionsklasse | Konstruktion | ||||
|---|---|---|---|---|---|
| Stahlbeton und Spannbeton mit Vorspannung ohne Verbund | Spannbeton mit Vorspannung mit nachträglichem Verbund | Spannbeton mit Vorspannung mit sofortigem Verbund | |||
| Einwirkungskombination | |||||
| quasi-ständig | häufig | häufig | selten | ||
| 1 | X0, XC1 | 0,4a) | 0,2 | 0,2 | - |
| 2 | XC2, XC3, XC4 | 0,3 | 0,2b),c) | 0,2b) | |
| 3 | XS1, XS2, XS3 XD1, XD2, XD3d) |
Dekompression | 0,2 | ||
| a)Bei den Expositionsklassen X0 und XC1 hat die Rissbreite keinen Einfluss auf die Dauerhaftigkeit und dieser Grenzwert wird i. Allg. zur Wahrung eines akzeptablen Erscheinungsbildes gesetzt. Fehlen entsprechende Anforderungen an das Erscheinungsbild, darf dieser Grenzwert erhöht werden. b)Zusätzlich ist der Nachweis der Dekompression unter der quasi-ständigen Einwirkungskombination zu führen. c)Wenn der Korrosionsschutz anderweitig sichergestellt wird (Hinweise hierzu in den Zulassungen der Spannverfahren), darf der Dekompressionsnachweis entfallen. d)Bei dieser Expositionsklasse können besondere Maßnahmen erforderlich sein. | |||||
Ermittlung der wirksamen Betonzugspannung
Spannung unter der Sohlpatte
Die Spannung unter Sohlplatte setzt sich nur aus dem Eigengewicht zusammen.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_0 = \gamma_G \cdot h \cdot \gamma_c = 1,35 \cdot 0,5 \cdot 25 = \underline{16,88 kN/m^2} }
Reibungsbeiwert
Verwendet wird ein Unterbeton mit Flügelglättung und 2 Lagen PE-Folie als Trennlage.
| 1 | 2 | 3 | |
| Unterkonstruktion a) | Trennlage | Reibungsbeiwert μ0 für die erste Verschiebung | |
|---|---|---|---|
| 1 | grobkörniger Baugrund ohne Sandbettung | keine | 1,4 … 2,1 e) |
| 2 | Kies-Sand-Bodenaustausch (nicht bindig) | bei Dicke der Bodenplatte h = 0,2m | > 1,4 |
| 3 | bei Dicke der Bodenplatte h = 0,8m | ≈ 0,9 | |
| 4 | sandiger Baugrund oder grobkörniger Baugrund mit Sandbettung unter der Sohlplatte | keine | 0,9 … 1,1 e) |
| 5 | Noppenbahn (d ≈ 0,6mm) | 0,8 … 1,0 d), e) | |
| 6 | 1 Lage PE-Folie b) | 0,5 … 0,7 d), e) | |
| 7 | Sandbett (Dicke 6 … 10cm, mittlere Korngröße 0,35mm) | keine (Direktauflagerung auf nicht feinkörnigem, bindigem Boden) | 0,7 |
| 8 | Perimeterdämmung auf Unterbeton bei beliebigem Baugrund | bei Dicke der Bodenplatte h ≤ 0,3m | ≈ 0,8 d) |
| 9 | bei Dicke der Bodenplatte h ≥ 0,8m | ≈ 0,5 d) | |
| 10 | Unterbeton abgezogen (makrorau) | 2 Lagen PE-Folie b) je 0,2mm: | |
| 11 | bei Dicke der Bodenplatte h = 0,3m | ≤ 2,0 | |
| 12 | bei Dicke der Bodenplatte h = 1,5m | ≤ 1,3 | |
| 13 | Bitumenschweißbahn c) | 0,35 … 0,7 d), e) | |
| 14 | Dickbitumen c) | 0,03 … 0,2 d), e) | |
| 15 | Trennschicht aus 2 Lagen dicker PE-Folie b) mit zwischenliegender Schicht aus Silikonfett als Schmiermittel | ≈ 0,8 | |
| 16 | Unterbeton mit Flügelglättung | 1 Lage PE-Folie b) | 0,8 … 1,4 d), e) |
| 17 | 2 Lagen PE- Folie b) | ≤ 0,8 | |
| 18 | mit PTFE b) beschichtete Folie | 0,2 … 0,5 e) | |
| 19 | Trennschicht aus 2 Lagen dicker PE-Folie b) mit zwischenliegender Schicht aus Silikonfett als Schmiermittel | ≈ 0,3 | |
| 20 | 1- bis 2-lagige Bitumenschweißbahn c), stumpf gestoßen: | ||
| 21 | bei Dicke der Bodenplatte h = 0,3m | ≈ 0,45 | |
| 22 | bei Dicke der Bodenplatte h > 1,0m | ≈ 0,2 | |
| 23 | Sicherheitsbeiwert für Reibung h) | γR = 1,35 f) | |
| 24 | γR =1,25 g) | ||
| 25 | Bemessungswert der Reibung | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_d = \gamma_R \cdot \mu_0 } | |
| a) Die Oberfläche der Unterkonstruktion muss den Anforderungen der Ebenheit nach DIN 18202 entsprechen. b) PE = Polyethylen, PTFE = Polytetrafluor- Ethylen c) Bituminöse Trennschichten sind nur bei ausreichender Schichtdicke und Temperaturen in der Trennschicht >10°C wirksam. d) Vorschlag der Autoren der Fachliteraturquellen e) Bewegt sich der Reibungsbeiwert in einer Spannbreite empfehlen die Autoren der Fachliteraturquellen die Annahme des höheren Wertes, wenn kein Einfluss auf die Ausführung besteht. f) nach "Lohmeyer Stahlbetonbau" [F 1] und "Weiße Wannen einfach und sicher - 9.Auflage" [F 2] g) nach "Weiße Wannen einfach und sicher - 11.Auflage"[F 3] h) Die Autoren der Fachliteraturquellen empfehlen mit den angegebenen Sicherheitsbeiwerten zu rechnen, da die Auswahl des Reibungsbeiwertes mit einiger Unsicherheit behaftet ist. | |||
Aus der Tabelle ergibt sich damit ein Bemessungswert der Reibung bei der sichereren Annahme des Teilsicherheitsbeiwertes γR = 1,35 [F 1] [F 2] von
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_d = 1,35 \cdot 0,8 = \underline{1,08} } .
Zugspannung in der Sohlplatte
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{ct,d} = \cfrac{\gamma_{ct} \cdot \mu_d \cdot \sigma_0 \cdot L}{2 \cdot a_{ct}} = \cfrac{1,0 \cdot 1,08 \cdot 16,88 \cdot 17,0}{2 \cdot 0,5 \cdot 1} = 309,92 kN/m^2 = \underline{0,31 N/mm^2} < f_{ct,eff} = 0,75 \cdot 3,2 = 2,4 N/mm^2 }
Da die Zwangsschnittgröße geringer als die wirksame Betonzugfestigkeit ist, darf die Bemessung der Mindestbewehrung zur Rissbreitenbegrenzung mit dem Bemessungswert der Betonzugspannungen σct,d durchgeführt werden.
Abschätzen der erforderlichen Bewehrung
Festigkeits-Zeitbeiwert

- Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \beta _{ct,vorh}={\cfrac {\sigma _{ct,d}}{f_{ctm}}}={\cfrac {0,31}{3,2}}={\underline {0,1}}}
Umrechnung der Bewehrung aus dem Diagramm
Bewehrung aus dem Diagramm: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{s,o,Diagr} = a_{s,u,Diagr} \approx 15,0 cm^2/m } mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_{ct,Diagr} = 0,5 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_{v,Diagr} = 40mm } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w_{k,Diagr} = 0,2mm}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_s \approx a_{s,Diagr} \cdot \sqrt{\cfrac{\beta_{ct,vorh} \cdot c_{v,vorh} \cdot w_{k,Diagr}}{\beta_{ct,Diagr} \cdot c_{v,Diagr} \cdot w_{k,vorh}}} = 15,0 \cdot \sqrt{\cfrac{0,1 \cdot 55 \cdot 0,2}{0,5 \cdot 40 \cdot 0,3}} = \underline{6,42 cm^2/m} }
Ermittlung der Mindestbewehrung zur Rissbreitenbegrenzung
Betondeckung und statische Nutzhöhe
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_v = c_{nom} = 55mm }
(aus der Statik)
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_1 = 55+\cfrac{16}{2} = 63 mm = \underline{6,3 cm} }
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d = h-d_1 = 50-6,3 = 43,7 cm }
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_v = c_{nom} = 55mm }
(aus der Statik)
Wirkungstiefe der Bewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{c,eff} = 2 \cdot b \cdot h_{c,ef} } mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b = 100 cm/m } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cfrac{h}{d_1} = \cfrac{50}{6,3} = 7,94 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle >5,0 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle <30,0 } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{c,ef} = 0,1 \cdot h+2,0 \cdot d_1 = 0,1 \cdot 50+2,0 \cdot 6,3 = 17,6 cm } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle < \cfrac{h}{2} = \cfrac{50}{2} = 25,0cm }
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{c,eff} = 2 \cdot 100 \cdot 17,6 = \underline{3520cm^2/m} }
Ermittlung der Beiwerte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_c = 1,0 } für reinen Zug Die Zugspannungen werden vom Bauteil selber hervorgerufen. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k = 0,8-20 \cdot \cfrac{0,8-0,5}{80-30} = 0,68 } Interpolation der in der DIN EN 1992-1-1[N 1] vorgegebenen Werte.
Ermittlung des Grenzdurchmessers
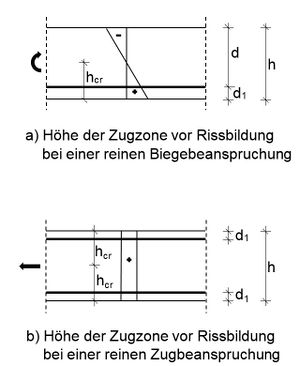
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing_S^* = \varnothing_S \cdot \cfrac{f_{ct,0}}{\sigma_{ct,d}} = 16 \cdot \cfrac{2,9}{0,31} = 150mm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing_S^* = \varnothing_S \cdot \cfrac{8 \cdot (h-d)}{k \cdot k_c \cdot h_{cr}} \cdot \cfrac{f_{ct,0}}{\sigma_{ct,d}} } mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (h-d) = d_1 } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{cr} = \cfrac{h}{2} = \cfrac{50}{2} = 25,0cm }
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing_S^* = 16 \cdot \cfrac{8 \cdot 6,3}{0,68 \cdot 1,0 \cdot 25} \cdot \cfrac{2,9}{0,31} = 444 mm}
- Der kleinere Wert ist maßgebend, d.h. der Grenzdurchmesser beträgt
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varnothing_S^* = \underline{150mm} } .
Ermittlung der Stahlspannung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_S = \sqrt{ \cfrac{6 \cdot w_k \cdot E_S \cdot f_{ct,0}}{\varnothing_S^*} } } mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_S = 200.000 N/mm^2 } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ct,0} = 2,9 N/mm^2 }
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_S = \sqrt{ \cfrac{6 \cdot 0,3 \cdot 200.000 \cdot 2,9}{150} } = \underline{83,43 N/mm^2} }
Ermittlung der Mindestbewehrung zur Rissbreitenbegrenzung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{s,min} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = \cfrac{k \cdot k_c \cdot a_{ct} \cdot \sigma_{ct,d}}{\sigma_S} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = \cfrac{0,68 \cdot 1,0 \cdot 50 \cdot 100 \cdot 0,31}{83,43} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = 12,63cm^2/m }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{s,min} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = \cfrac{a_{ct,eff} \cdot \sigma_{ct,d}}{\sigma_S} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ge \cfrac{k \cdot a_{ct} \cdot f_{ct,eff}}{f_{yk}} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = \cfrac{2600 \cdot 0,31}{83,43} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ge \cfrac{0,68 \cdot 50 \cdot 100 \cdot 0,31}{500} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = 13,08 cm^2/m } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle > 2,11cm^2/m }
Da es sich um eine Mindestbewehrung handelt, ist der kleinere Wert maßgebend, d.h. zur Begrenzung der Rissbreite müssen
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{12,63 cm^2/m} }
eingelegt werden.
Vergleich der abgeschätzten mit der errechneten Bewehrung
Das Abschätzen der Bewehrung mit den Diagrammen nach Meyer & Meyer ist sehr genau und damit für einen ersten Überschlag geeignet.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{s,o} = a_{s,u} = \cfrac{12,63}{2} = 6,32 cm^2/m \approx 6,42 cm^2/m}
Da die rechnerische Mindestbewehrung zur Rissbreitenbegrenzung geringer als die statisch erforderliche Bewehrung ist, müssen keine weiteren Bewehrungseisen eingelegt werden.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{s,o} = a_{s,u} = 6,32 cm^2/m < 10,05 cm^2/m}
Vergleich mit dem Beispiel "Zwang - Mindestbewehrung zur Rissbreitenbegrenzung für eine Sohlplatte (Bsp.)"
Kann die Verringerung der Zwangsbeanspruchung nicht angewendet werden, weil z.B. der späte Zwang nicht ausgeschlossen werden kann, ist die benötigte Bewehrungsmenge zur Begrenzung der Rissbreiten deutlich größer.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{s,min} = 12,63 cm^2/m < 34,81 cm^2/m }
Quellen
- Fachliteratur
- ↑ 1,0 1,1 1,2 1,3 1,4 Baar, S.; Ebeling, K.: Lohmeyer Stahlbetonbau. Bemessung - Konstruktion - Ausführung. 10.Auflage. Wiesbaden 2017
- ↑ 2,0 2,1 2,2 Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 9. überarbeitete und erweiterte Auflage. Düsseldorf 2009
- ↑ 3,0 3,1 Lohmeyer, G.; Ebeling, K.: Weiße Wannen - einfach und sicher. Konstruktion und Ausführung wasserundurchlässiger Bauwerke aus Beton. 11. überarbeitete Auflage. Düsseldorf 2018
- ↑ Fingerloos, F.; Hegger, J.; Zilch, K.: EUROCODE 2 für Deutschland. Kommentierte und konsolidierte Fassung. 2., überarbeitete Auflage. Beuth Verlag GmbH 2016
- Normen