Verformungsnachweis - direkte Berechnung: Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) K |
EWill (Diskussion | Beiträge) K (EWill verschob die Seite Direkte Verformungsberechnung - biegebeanspruchte Bauteile nach Verformungsnachweis - direkte Berechnung: zuvor ungünstige Einordnung auf der Übersichtsseite) |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Im Rahmen der Nachweise im Grenzzustand der Gebrauchstauglichkeit ist auch ein [[Verformungsnachweis]] zu führen. Dieser kann [[ | + | Im Rahmen der Nachweise im Grenzzustand der Gebrauchstauglichkeit ist auch ein [[Verformungsnachweis]] zu führen. Dieser kann [[Indirekte Verformungsberechnung - biegebeanspruchte Bauteile|indirekt über die Biegeschlankheit]] geführt werden oder über eine direkte Verformungsberechnung. Die direkte Verformungsberechnung ist zwar aufwendiger, ergibt im Vergleich zum indirekten Verformungsnachweis aber genauere Ergebnisse. |
<br /> | <br /> | ||
| Zeile 69: | Zeile 69: | ||
:{| | :{| | ||
|- | |- | ||
| − | | <math> \beta</math> … || Koeffizient zur Berücksichtigung der Belastungsdauer und der Lastwiederholungen (<math> \beta=0</math> bei Kurzzeitbelastung; <math> \beta=0,5</math> bei Langzeitbelastung oder vielen Zyklen wiederholender Belastung) | + | | <math> \beta</math> … || Koeffizient zur Berücksichtigung der Belastungsdauer und der Lastwiederholungen (<math> \beta=1,0</math> bei Kurzzeitbelastung; <math> \beta=0,5</math> bei Langzeitbelastung oder vielen Zyklen wiederholender Belastung) |
|- | |- | ||
| <math> \sigma_{sr} </math> … || die Spannung in der Zugbewehrung bei Annahme eines gerissenen Querschnitts unter einer Einwirkungskombination, die zur Erstrissbildung führt | | <math> \sigma_{sr} </math> … || die Spannung in der Zugbewehrung bei Annahme eines gerissenen Querschnitts unter einer Einwirkungskombination, die zur Erstrissbildung führt | ||
| Zeile 83: | Zeile 83: | ||
Der Krümmungsverlauf ist affin zum Momentenverlauf. Die Beziehungen zwischen Momenten und Krümmungen lassen sich mithilfe der [[Momenten-Krümmungs-Beziehungen]] beschreiben. | Der Krümmungsverlauf ist affin zum Momentenverlauf. Die Beziehungen zwischen Momenten und Krümmungen lassen sich mithilfe der [[Momenten-Krümmungs-Beziehungen]] beschreiben. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=Statisch bestimmte Systeme= | =Statisch bestimmte Systeme= | ||
| Zeile 159: | Zeile 105: | ||
| <math> E_{c,eff}</math> … || effektives Elastizitätsmodul (Berücksichtigung des Kriechens) | | <math> E_{c,eff}</math> … || effektives Elastizitätsmodul (Berücksichtigung des Kriechens) | ||
|- | |- | ||
| − | | <math> I_{I}</math> … || Trägheitsmoment im Zustand I | + | | <math> I_{I}=k_I\cdot\frac{b*h^3}{12}</math> … || Trägheitsmoment im Zustand I |
| + | |- | ||
| + | | <math> k_{I}</math> … || Steifigkeitsbeiwert im Zustand I (vgl. Grafik) | ||
|}</li> | |}</li> | ||
| + | |||
| + | <math>k_I=1+12\cdot\left(0,5-\xi^I\right)^2+12\cdot\alpha_e\cdot\rho^I\cdot\left(\frac{d}{h}-\xi^I\right)^2</math> (gilt nur für Rechteckquerschnitte ohne Druckbewehrung) | ||
| + | |||
| + | <math>\xi^I=\frac{0,5+\alpha_e\cdot\rho^I\cdot\frac{d}{h}}{1+\alpha_e\cdot\rho^I}</math> | ||
| + | |||
| + | <math>\rho^I=\frac{A_{s1}}{b\cdot h}</math> | ||
<math>E_{c,eff}=\frac{E_{cm}}{1+\phi_{\infty,t_0}}</math> | <math>E_{c,eff}=\frac{E_{cm}}{1+\phi_{\infty,t_0}}</math> | ||
| Zeile 172: | Zeile 126: | ||
|}</li> | |}</li> | ||
<br /> | <br /> | ||
| + | |||
| + | Der angegebene Steifigkeitsbeiwert im Zustand I kann entweder mit der angegebene Formel oder mit dem weiter unten folgenden Diagramm ermittelt werden. Hierbei kommt es zu geringen Abweichungen zwischen beiden Varianten, da dem Diagramm nach TROST <ref name="trost69">Trost, H. et al.: Zweckmäßige Ermittlung der Durchbiegung von Stahlbetonträgern; Beton- und Stahlbetonbau 64 (1969), Heft 6</ref> eine vereinfachte Gleichung für <math>k_I</math> zugrunde liegt. | ||
Anschließend wird die Krümmung an der Stelle des maximalen Moments für den vollständig gerissenen Querschnitt ermittelt. | Anschließend wird die Krümmung an der Stelle des maximalen Moments für den vollständig gerissenen Querschnitt ermittelt. | ||
| Zeile 225: | Zeile 181: | ||
Nach diesen Schritten werden die Krümmungen infolge Schwinden im Zustand I und II ermittelt. | Nach diesen Schritten werden die Krümmungen infolge Schwinden im Zustand I und II ermittelt. | ||
| − | [[Datei:Durchbiegungsermittlung_- | + | [[Datei:Durchbiegungsermittlung_-_biegebeanspruchte_Bauteile_9.jpg|300px|thumb|right|Steifigkeitsbeiwert für den Zustand II nach TROST<ref name="trost69"></ref>]] |
<math> \kappa_{cs}=\left(\frac{1}{r}\right)_{cs}=\varepsilon_{cs}\cdot\alpha_e\cdot\frac{S}{I} </math> | <math> \kappa_{cs}=\left(\frac{1}{r}\right)_{cs}=\varepsilon_{cs}\cdot\alpha_e\cdot\frac{S}{I} </math> | ||
| Zeile 246: | Zeile 202: | ||
| <math> k_{II} </math> … || Steifigkeitsbeiwert für den Zustand II (vgl. Grafik) | | <math> k_{II} </math> … || Steifigkeitsbeiwert für den Zustand II (vgl. Grafik) | ||
|}</li> | |}</li> | ||
| + | |||
| + | <math>k_{II}=4\cdot(\xi^{II})^3+12\cdot\alpha_e\cdot \rho^{II}\cdot\left(1-\xi^{II}\right)^2</math> | ||
| + | |||
| + | <math>\xi^{II}=-\alpha_e\cdot\rho^{II}+\sqrt{\left(\alpha_e\cdot\rho^{II}\right)^2+2\cdot\alpha_e\cdot\rho^{II}}</math> | ||
| + | |||
| + | <math>\rho^{II}=\frac{A_{s1}}{b\cdot d}</math> | ||
Mit diesen beiden Werten und dem Verteilungsbeiwert kann der wahrscheinliche Wert der Krümmung infolge Schwinden ermittelt werden. | Mit diesen beiden Werten und dem Verteilungsbeiwert kann der wahrscheinliche Wert der Krümmung infolge Schwinden ermittelt werden. | ||
| Zeile 287: | Zeile 249: | ||
Simpsonregel: | Simpsonregel: | ||
| − | <math>w(x)=\int_{}^{}(\overline{M}(x) \cdot \kappa) dx = \frac{\Delta}{ | + | <math>w(x)=\int_{}^{}(\overline{M}(x) \cdot \kappa) dx = \frac{\Delta x}{3}\cdot\left(y_0+4y_1+2y_2+....+2y_{n-2}+4y_{n-1}+y_n\right)</math> |
wobei: | wobei: | ||
Aktuelle Version vom 11. Januar 2025, 23:43 Uhr
Im Rahmen der Nachweise im Grenzzustand der Gebrauchstauglichkeit ist auch ein Verformungsnachweis zu führen. Dieser kann indirekt über die Biegeschlankheit geführt werden oder über eine direkte Verformungsberechnung. Die direkte Verformungsberechnung ist zwar aufwendiger, ergibt im Vergleich zum indirekten Verformungsnachweis aber genauere Ergebnisse.
Allgemeines
Grundsätzlich bietet sich die direkte Verformungsberechnung immer dann an, wenn eine genauere Kenntnis der sich ergebenden Verformung erforderlich ist. Die direkte Verformungsberechnung kann vor allem unter folgenden Bedingungen sinnvoll sein:
- schlanke bzw. schwingungsanfällige Bauteile
- hoch ausgenutzte Bauteile
- Decken mit hohen Einzellasten bei gleichzeitiger flächiger Verkehrslast
- Bauteile bei denen Verformungen zum Verlust der Funktionsfähigkeit führen können (z.B. Bauteile unter Maschinen, Flachdächer (Entwässerung))
- Bauteile deren Verformungen Schäden an angrenzenden Bauteilen hervorrufen können (z.B. Risse in Wänden auf dem Bauteil, Schäden Glasfassaden bzw. Schaufenstern)
Im Folgenden wird das numerische Verfahren und das Näherungsverfahren näher erläutert, anschließend wird auf die Durchbiegungsberechnung bei statisch unbestimmten Systemen eingegangen. Alle vorgestellten Verfahren sind gemäß EC 2 zulässig für die direkte Verformungsberechnung.
Materialkennwerte
Die Genauigkeit der verwendeten Werkstoffmodelle ist der Genauigkeit der Verformungsberechnung anzupassen. Wird ein genaues Berechnungsmodell verwendet aber die Werkstoffeigenschaften nicht realitätsnah genug beschrieben, entsteht ein hoher Aufwand für ein weniger genaues Ergebnis.
Für das Elastizitätsmodul und die Festigkeitswerte von Beton sind Mittelwerte zu verwenden. Im Bereich von sigma_c<0,4 f_ck kann davon ausgegangen werden, dass sich der Beton linear-elastisch verhält. Da im Grenzzustand der Gebrauchstauglichkeit i.d.R. davon ausgegangen werden kann, dass diese Grenze nicht überschritten wird, kann ein linear-elastisches Tragverhalten für den Beton angenommen werden.
Für den Stahl darf eine bilinearen Spannungsdehnungslinie angenommen werden.
Grundlagen
Zusammenhang Belastung - Steifigkeit - Krümmung
Gemäß den allgemeinen Zusammenhängen der Mechanik sind die Krümmung abhängig von der Belastung und der Steifigkeit:
Die Durchbiegung ergibt sich durch zweifache Integration der Krümmung:
Die Durchbiegung ist dementsprechend abhängig von der Systemlänge, der Belastung und der Steifigkeit. Unter Annahme eines zum Krümmungsverlauf affinen Momentenverlaufes lässt sich das Doppelintegral der Krümmung unter zur Hilfenahme des Prinzips der virtuellen Kräfte zu folgendem Ausdruck umstellen:
Die virtuelle Kraft für die Bestimmung der virtuellen Momente ist an der Stelle aufzubringen, an der die Verformung berechnet werden soll.
Steifigkeit
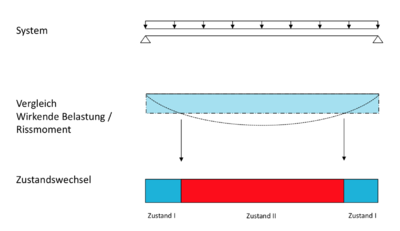
Die Verformungen von Stahlbetonbauteilen sind maßgeblich von der Steifigkeit abhängig. Diese wird stark vom Stand der Rissbildung abhängig, im Rahmen des Rissbildungsprozesses kommt es zum Abfall der Steifigkeit. Nimmt die Steifigkeit ab, nehmen die Verformungen zu. Die Steifigkeit eines Bauteils im Zustand II (abgeschlossene Rissbildung) ist geringer als im Zustand I (umgerissen). Näheres zum Prozess der Rissbildung kann der Seite zur Biegebemessung entnommen werden.
Die Verformungsberechnung von Stahlbetonbauteilen wird dadurch erschwert, dass sich nicht das ganze Bauteil im Zustand I bzw. II befindet, sodass die Steifigkeiten abschnittsweise differieren. Vereinfachend wird in der Durchbiegungsberechnung bei der Ermittlung der Steifigkeiten nur zwischen dem umgerissenen und dem vollständig gerissenen Zustand unterschieden. Die Steifigkeit während des Rissbildungsprozesses wird vernachlässigt [1].
Durch die Vernachlässigung des Rissbildungsprozesses bei der Berechnung kommt es an der Grenze zwischen dem Bereich im Zustand I und dem im Zustand II zu einem sprunghaften Abfall der Steifigkeit; würde er berücksichtigt werden, fände der Abfall der Steifigkeit kontinuirlich statt. Vernachlässigt man den Rissbildungsprozess wird die Steifigkeit unterschätzt, sodass die Vernachlässigung auf der sichern Seite liegende Ergebnisse ergibt.
wobei:
… untersuchter Dehnungsparameter (Dehnung, Krümmung oder Rotation) … untersuchter Dehnungsparameter im Zustand I … untersuchter Dehnungsparameter im Zustand II … Verteilungsbeiwert zur Berücksichtigung der Rissbildung und der Mitwirkung des Betons zwischen den Rissen
Für ungerissene Querschnitte ist der Verteilungsbeiwert ; für gerissene Querschnitte ergibt er sich nach folgender Gleichung:
wobei:
… Koeffizient zur Berücksichtigung der Belastungsdauer und der Lastwiederholungen ( bei Kurzzeitbelastung; bei Langzeitbelastung oder vielen Zyklen wiederholender Belastung) … die Spannung in der Zugbewehrung bei Annahme eines gerissenen Querschnitts unter einer Einwirkungskombination, die zur Erstrissbildung führt … die Spannung in der Zugbewehrung bei Annahme eines gerissenen Querschnitts (Spannung im Riss)
Eine Zusammenfassung der Querschnittswerte für den Zustand I und Zustand II lässt sich der Literatur entnehmen [2].
Krümmung
Eine Krümmung entsteht bei unterschiedlichen Dehnungen an der Ober- und Unterkante des Bauteils. Im Zustand I ist sie abhängig von der Betondehnung an der Unterkante und der Betonstauchung an der Oberkante, im Zustand II von der Betonstauchung an der Oberkante und der Dehnung der Zugbewehrung. Für die Krümmungen sind im allgemeinen die gleichen Einflussgrößen maßgebend wie für die Verformungen.
Der Krümmungsverlauf ist affin zum Momentenverlauf. Die Beziehungen zwischen Momenten und Krümmungen lassen sich mithilfe der Momenten-Krümmungs-Beziehungen beschreiben.
Statisch bestimmte Systeme
Näherungsverfahren nach EC2
Im Näherungsverfahren wird von einer konstanten Steifigkeit über das gesamte Bauteil ausgegangen. Die Krümmungen im Zustand I und II werden am Punkt der maximalen Belastung ermittelt und auf die gesamte Länge übertragen [3]. Die Berücksichtigung unterschiedlicher Querschnitte über die Bauteillänge ist mit dem Näherungsverfahren nicht möglich.
Die Verformungsberechnung mithilfe des Näherungsverfahrens läuft folgendermaßen ab:
Im ersten Schritt wird die Krümmung im Zustand I an der Stelle des Maximalmoments ermittelt.
wobei:
… Krümmung im Zustand I … einwirkendes Moment … effektives Elastizitätsmodul (Berücksichtigung des Kriechens) … Trägheitsmoment im Zustand I … Steifigkeitsbeiwert im Zustand I (vgl. Grafik)
(gilt nur für Rechteckquerschnitte ohne Druckbewehrung)
wobei:
… mittleres Elastizitätsmodul … Kriechzahl
Der angegebene Steifigkeitsbeiwert im Zustand I kann entweder mit der angegebene Formel oder mit dem weiter unten folgenden Diagramm ermittelt werden. Hierbei kommt es zu geringen Abweichungen zwischen beiden Varianten, da dem Diagramm nach TROST [4] eine vereinfachte Gleichung für zugrunde liegt.
Anschließend wird die Krümmung an der Stelle des maximalen Moments für den vollständig gerissenen Querschnitt ermittelt.
wobei:
… Krümmung im Zustand II … Stahldehnung im Zustand II … statische Nutzhöhe … Druckzonenhöhe im Zustand II
wobei:
… Verhältnis der Elastizitätsmoduli … Längsbewehrungsgrad … Bewehrungsquerschnittsfläche
Darauf folgend kann mithilfe des Verteilungsbeiwerts der wahrscheinliche Wert der Krümmung ermittelt werden. Statt über die Spannungen kann der Verteilungsbeiwert auch mithilfe des einwirkenden Moments und des Rissmoments ermittelt werden.
wobei:
… Anrissspannung im Zustand II … Rissbildungsmoment … Betonzugfestigkeit … Abstand des Schwerpunkts vom Zugrand
Für nähere Erläuterungen zum Verteilungsbeiwert vgl. oben.
Nach diesen Schritten werden die Krümmungen infolge Schwinden im Zustand I und II ermittelt.

wobei:
… Krümmung infolge Schwinden … Schwindmaß … Flächenmoment 1. Grades der Querschnittsfläche der Bewehrung, bezogen auf den Schwerpunkt des Querschnitts im Zustand I … Flächenmoment 1. Grades der Querschnittsfläche der Bewehrung, bezogen auf den Schwerpunkt des Querschnitts im Zustand II … Flächenträgheitsmoment im Zustand I … Flächenträgheitsmoment im Zustand II … Steifigkeitsbeiwert für den Zustand II (vgl. Grafik)
Mit diesen beiden Werten und dem Verteilungsbeiwert kann der wahrscheinliche Wert der Krümmung infolge Schwinden ermittelt werden.
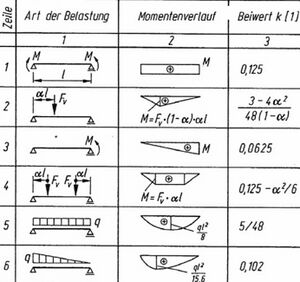
Im letzten Schritt werden die einzelnen Krümmungsanteile addiert und schlussendlich aus der Gesamtkrümmung die Durchbiegung berechnet.
wobei:
… Durchbiegung … Beiwert für die Momentenverteilung (vgl. Grafik) … Systemlänge
Beispiel für die Verformungsberechnung mithilfe des Näherungsverfahrens
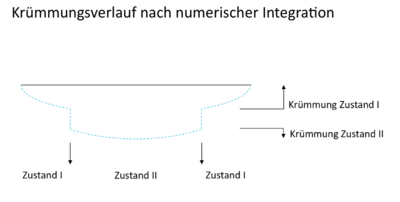
Numerische Integration
Die numerische Integration stellt eine weitere Möglichkeit zur Berechnung der Verformungen eines Bauteils dar. Im Rahmen dieses Verfahrens werden die Krümmungen über die Bauteillänge integriert, die Krümmungen in den betrachteten Abschnitten werden mitthilfe der Momenten-Krümmungs-Beziehungen bestimmt. Der größere Rechenaufwand ermöglicht eine genauere Berücksichtigung der unterschiedlichen Beanspruchung über die Bauteillänge.
Die grundlegende Annahme ist auch hier der Zusammenhang aus Krümmung, Belastung und Steifigkeit des Querschnittes:
(Herleitung siehe oben)
Die Integration kann als numerische Integration mithilfe der Newton-Cotes Formeln erfolgen, dies eignet sich besonders gut für eine computerbasierte Umsetzung. Die gebräuchlichsten Verfahren sind die Trapez- und die Simpsonregel.
Simpsonregel:
wobei:
… Länge eines Intervalls
Das Bauteil wird in eine beliebige Anzahl an Intervallen unterteilt, bei Verwendung der Simpsonregel muss die Anzahl der Intervalle gerade bzw. die Anzahl der Stützstellen ungerade sein. Je höher die Anzahl der betrachteten Querschnitte gewählt wird, desto genauer lässt sich die Durchbiegung ermitteln. Für eine genaue Näherung an die Durchbiegung reicht bereits eine Unterteilung in 9 Stützstellen bzw. 8 Intervalle aus. Eine Vergrößerung der Einteilung liefert letztlich nur geringe Verbesserungen, die den erheblich größeren Rechenaufwand nicht rechtfertigen.
Für jeden betrachteten Querschnitt werden die virtuellen Momentenschnittgrößen sowie die Krümmung ermittelt. Die virtuellen Momente sind abhängig vom Ort der Verformungsermittlung und dem statischen System, die Krümmungen von der Belastung (vgl. Momenten-Krümmungs-Beziehungen).
Bei symmetrischen Systemen mit symmetrischer Belastung ist die Betrachtung einer Bauteilhälfte ausreichend.
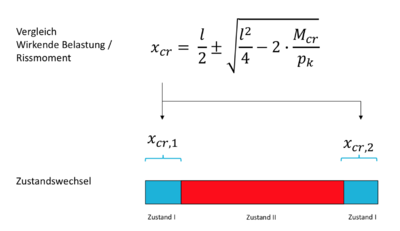
Eine Differenzierung zwischen den Zuständen I und II lässt sich über folgenden Ausdruck ermitteln[6]:
Mcr Rissmoment pk Belastung
Der Ansatz liefert zwei Ordinaten: erstere gibt Aufschluss über den Wechsel von Zustand I in den Zustand II; zweitere gibt Aufschluss über den Wechsel von Zustand II in den Zustand I.
Beispiel für die Verformungsberechnung mithilfe der numerischen Integration
Statisch unbestimmte Systeme
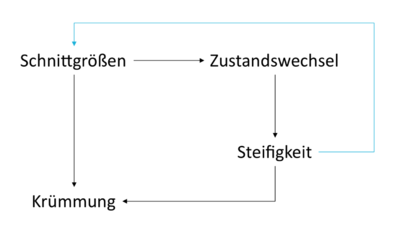
Bei statisch unbestimmten Systemen steht die Schnittgrößenverteilung in einem direkten Zusammenhang mit der Steifigkeitsverteilung. Diese wiederum ist maßgeblich abhängig von der Rissbildung und somit von der Größe der Bereiche im Zustand I bzw. II. Aufgrund dieses Zusammenhangs ist nur eine iterative Berechnung der Durchbiegung möglich.
In einem ersten Schritt können für eine frei wählbare Steifigkeitsverteilung die Schnittgrößen ermittelt werden. Anschließend wird für diese Schnittgrößenverteilung die Größe der Bereiche im Zustand I bzw. II festgelegt und die sich hieraus ergebende Steifigkeitsverteilung mit der angenommenen verglichen. Ist die Differenz zwischen angenommener und berechneter Steifigkeitsverteilung zu groß, wird der Vorgang mit der neuen, berechneten Steifigkeitsverteilung wiederholt.
Dieser Vorgang wird so lange wiederholt, bis die Differenz ausreichend gering ist. Das akzeptierte Maß dieser Differenz ist frei wählbar, je kleiner sie ist, desto größer ist die Genauigkeit.
Wenn die Iteration beendet ist, kann die Durchbiegung wie bereits besprochen durch numerische Integration Krümmungen über die Bauteillänge oder mit dem Näherungsverfahren berechnet werden.
Wegen des hohen Aufwands und der Fehleranfälligkeit einer händischen Berechnung bietet sich für die direkte Verformungsberechnung statisch unbestimmter Systeme eine computerbasierte Umsetzung an.
Quellen
- ↑ DIN EN 1992-1-1, Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken - Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, Beuth-Verlag, 2011
- ↑ Goris, Alfons; Bender, Michél: Stahlbetonbau-Praxis nach Eurocode 2, Band 1, 6. Überarbeitete und erweiterte Auflage. Berlin: Beuth Verlag GmbH; S. 270, 271
- ↑ Goris, Alfons; Bender, Michél: Stahlbetonbau-Praxis nach Eurocode 2, Band 1, 6. Überarbeitete und erweiterte Auflage. Berlin: Beuth Verlag GmbH; S. 300ff
- ↑ 4,0 4,1 Trost, H. et al.: Zweckmäßige Ermittlung der Durchbiegung von Stahlbetonträgern; Beton- und Stahlbetonbau 64 (1969), Heft 6
- ↑ Litzner, H.-U.: Grundlagen der Bemessung nach Eurocode 2, BK 1995
- ↑ Strohbusch, Jens: Beitrag zur Verformungsberechnung im Stahlbetonbau mit kritischer Bewertung bestehender Regelungen. Universität Siegen, Fachbereich Bauingenieurwesen, Dissertation, 2010; S. 95
Seiteninfo
|