Momenten-Krümmungs-Beziehungen: Unterschied zwischen den Versionen
EWill (Diskussion | Beiträge) K |
EWill (Diskussion | Beiträge) K |
||
| Zeile 3: | Zeile 3: | ||
<br /> | <br /> | ||
=Allgemeines= | =Allgemeines= | ||
| − | Im Zustand I ist der Zusammenhang zwischen Momenten und Krümmungen linear. Durch die Rissbildung kommt es zu einer | + | Im Zustand I ist der Zusammenhang zwischen Momenten und Krümmungen linear. Durch die Rissbildung kommt es zu einer schlagartigen Zunahme der Krümmungen. Im Zustand II sind die Krümmungen wieder annähernd linear. Die [[Mitwirkung des Betons zwischen den Rissen (Zugversteifung)|Mitwirkung des Betons zwischen den Rissen]] hat maßgeblich Einfluss auf die Größe der Krümmungen; durch diese nimmt die Stahldehnung zwischen den Rissen und somit auch die mittlere Krümmung deutlich ab <ref name="zilch06">Zilch,K., Zehetmaier,G.: Bemessung im konstruktiven Betonbau; 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006</ref>. |
| − | Nach Überschreitung der Streckgrenze nimmt das Moment kaum noch, die Krümmungen allerdings noch deutlich zu bevor schlussendlich das Versagen des Bauteils eintritt und die Momenten-Krümmungs-Linie endet. Die maximal erreichbare Krümmung ist abhängig vom Grenzbewehrungsgrad. Dies ist der Punkt, an dem das Versagen vom Stahl- zum Betonversagen wechselt. Die maximale erreichbare Krümmung tritt | + | Nach Überschreitung der Streckgrenze nimmt das Moment kaum noch, die Krümmungen allerdings noch deutlich zu bevor schlussendlich das Versagen des Bauteils eintritt und die Momenten-Krümmungs-Linie endet. Die maximal erreichbare Krümmung ist abhängig vom Grenzbewehrungsgrad. Dies ist der Punkt, an dem das Versagen vom Stahl- zum Betonversagen wechselt. Die maximale erreichbare Krümmung tritt beim Grenzbewehrungsgrad auf, darüber bzw. darunter nehmen die Krümmungen ab, da nicht die maximal mögliche Betonstauchung bzw. Stahldehnung aktiviert wird. Der Grenzbewehrungsgrad ist abhängig von der Querschnittsgeometrie und der Betonfestigkeit. |
Die Momenten-Krümmungs-Beziehungen lassen sich vereinfachend durch einen trilinearen Verlauf darstellen <ref name="DAfStb600"></ref>. Die kennzeichnenden Punkte sind dabei das Rissmoment, das Biegemoment bei Erreichen der Fließgrenze und das Bruchmoment. Für jeden Querschnitt mit abweichender Geometrie oder Bewehrungsmenge sind eigene Momenten-Krümmungs-Beziehungen zu berechnen. | Die Momenten-Krümmungs-Beziehungen lassen sich vereinfachend durch einen trilinearen Verlauf darstellen <ref name="DAfStb600"></ref>. Die kennzeichnenden Punkte sind dabei das Rissmoment, das Biegemoment bei Erreichen der Fließgrenze und das Bruchmoment. Für jeden Querschnitt mit abweichender Geometrie oder Bewehrungsmenge sind eigene Momenten-Krümmungs-Beziehungen zu berechnen. | ||
| Zeile 136: | Zeile 136: | ||
==Krümmung im gerissenen Zustand unter den Bruchschnittgrößen== | ==Krümmung im gerissenen Zustand unter den Bruchschnittgrößen== | ||
| − | Das Bruchmoment und die dazugehörige Dehnung können mithilfe der ω-Tafeln oder iterativ ermittelt werden. Als Festigkeit für die Bewehrung ist die Zugfestigkeit zu verwenden. | + | Das Bruchmoment und die dazugehörige Dehnung können mithilfe der [[Biegebemessung (einachsige Biegung)|ω-Tafeln]] oder iterativ ermittelt werden. Als Festigkeit für die Bewehrung ist die Zugfestigkeit zu verwenden. |
<math>\kappa_t=\frac{\mid \varepsilon_{st}\mid+\mid\varepsilon_{ct}\mid}{d}</math> | <math>\kappa_t=\frac{\mid \varepsilon_{st}\mid+\mid\varepsilon_{ct}\mid}{d}</math> | ||
Version vom 30. Juni 2024, 20:49 Uhr
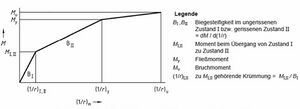
Die Momenten Krümmungs-Beziehungen beschreiben den Zusammenhang zwischen dem einwirkenden Moment und der dadurch auftretenden Krümmung.
Allgemeines
Im Zustand I ist der Zusammenhang zwischen Momenten und Krümmungen linear. Durch die Rissbildung kommt es zu einer schlagartigen Zunahme der Krümmungen. Im Zustand II sind die Krümmungen wieder annähernd linear. Die Mitwirkung des Betons zwischen den Rissen hat maßgeblich Einfluss auf die Größe der Krümmungen; durch diese nimmt die Stahldehnung zwischen den Rissen und somit auch die mittlere Krümmung deutlich ab [2].
Nach Überschreitung der Streckgrenze nimmt das Moment kaum noch, die Krümmungen allerdings noch deutlich zu bevor schlussendlich das Versagen des Bauteils eintritt und die Momenten-Krümmungs-Linie endet. Die maximal erreichbare Krümmung ist abhängig vom Grenzbewehrungsgrad. Dies ist der Punkt, an dem das Versagen vom Stahl- zum Betonversagen wechselt. Die maximale erreichbare Krümmung tritt beim Grenzbewehrungsgrad auf, darüber bzw. darunter nehmen die Krümmungen ab, da nicht die maximal mögliche Betonstauchung bzw. Stahldehnung aktiviert wird. Der Grenzbewehrungsgrad ist abhängig von der Querschnittsgeometrie und der Betonfestigkeit.
Die Momenten-Krümmungs-Beziehungen lassen sich vereinfachend durch einen trilinearen Verlauf darstellen [1]. Die kennzeichnenden Punkte sind dabei das Rissmoment, das Biegemoment bei Erreichen der Fließgrenze und das Bruchmoment. Für jeden Querschnitt mit abweichender Geometrie oder Bewehrungsmenge sind eigene Momenten-Krümmungs-Beziehungen zu berechnen.
In der Regel erfordern Nachweise im Zusammenhang mit den Momenten-Krümmungs-Beziehungen realitätsnahe Ergebnisse. Aufgrund dessen werden in der Regel die rechnerischen Mittelwerte der Festigkeiten für die Ermittlung der Momenten-Krümmungs-Beziehungen verwendet.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{cR}=0,85\cdot\alpha_{cc}\cdot f_{ck}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{yR}=1,1\cdot f_{yk}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{tR}=1,05\cdot f_{yR}} (für B500A)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{tR}=1,08\cdot f_{yR}} (für B500B)
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{cR} } … rechnerischer Mittelwert der Betondruckfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ck} } … charakteristische Betondruckfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{yR} } … rechnerischer Mittelwert der Festigkeit an der Streckgrenze des Stahls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{yk} } … charakteristischer Wert der Festigkeit an der Streckgrenze des Stahls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{tR} } … rechnerischer Mittelwert Zugfestigkeit des Stahls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha_{cc}=0,85 } … Faktor zur Berücksichtigung von Langzeiteinwirkungen
Berechnung
Erstrissbildung
Das Rissbildungsmoment kann mit der gewohnten Gleichung ermittelt werden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{cr}=\frac{f_{ctm}\cdot I_I}{z_{I,c1}}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{cr} } … Rissbildungsmoment Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ctm} } … mittlere Zugfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_I } … Flächenträgheitsmoment im Zustand I Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_{I,c1} } … Schwerachsenabstand bis zum Zugrand
Die erforderlichen Dehnungen lassen sich mit den folgenden Gleichungen ermitteln:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{c1,cr1}=\frac{f_{ctm}}{E_{cm}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{c2,cr1}=-\varepsilon_{c1,cr1}\cdot\frac{z_{I,c2}}{z_{I,c1}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{s,cr1}=\varepsilon_{c1,cr1}\cdot\frac{d-z_{I,c2}}{z_{I,c1}}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{c1,cr1} } … Betondehnung am Zugrand im ungerissenen Zustand unter Rissschnittgrößen bei Erreichen von fctm Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{c2,cr1} } … Betondehnung am Druckrand im ungerissenen Zustand unter Rissschnittgrößen bei Erreichen von fctm Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{s,cr1} } … Stahldehnung im ungerissenen Zustand unter Rissschnittgrößen bei Erreichen von fctm Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_{cm} } … mittleres Elastizitätsmodul Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_{I,c2} } … Schwerachsenabstand bis zum Druckrand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d } … statische Nutzhöhe
Die Krümmung am Punnkt der Erstrissbildung kann mithilfe der folgenden Gleichung berechnet werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_I=\frac{\mid \varepsilon_{s,cr1}\mid+\mid\varepsilon_{c2,cr1}\mid}{d}=\frac{\mid \varepsilon_{c1,cr1}\mid+\mid\varepsilon_{c2,cr1}\mid}{h}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_I } … Krümmung unter dem Rissbildungsmoment im ungerissenen Zustand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h } … Bauteilhöhe
Krümmung im gerissenen Zustand bei Erreichen der Streckgrenze des Betonstahls
Das Streckgrenzenmoment ergibt sich, wenn bei der Biegebemessung die Stahldehnung der Dehnung an der Streckgrenze entspricht. Da den gewöhnlichen Bemessungshilfsmitteln (vgl. Biegebemessung) nicht die Dehnung an der Streckgrenze zugrunde liegt, sondern die bei Erreichen der Zugfestigkeit, sind diese Hilfsmittel für die Ermittlung des Streckgrenzenmoments nicht geeignet. Entweder ist eine iterative Berechnung ohne Bemessungshilfsmittel durchzuführen (vgl. Biegebemessung) oder es sind spezielle Bemessungstafeln zu verwenden z.B. die von Schmitz.
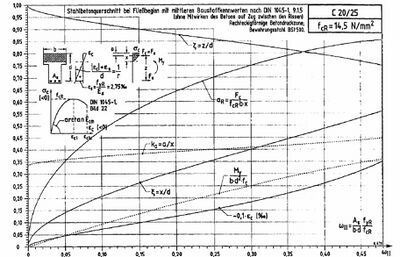
Die Gleichungen für die Ermittlung des Moments an der Streckgrenze und die Betonstauchung sind der beigefügten Tafel zu entnehmen. Die Stahldehnung ergibt sich mithilfe der folgenden Gleichungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{sy}=\frac{f_{yR}}{E_s}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{sy} } … Stahldehung bei Erreichend der Streckgrenze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_s } … Elastizitätsmodul des Stahls
Die Krümmung kann mithilfe der folgenden Gleichung ermitelt werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_y=\frac{\mid \varepsilon_{sy}\mid+\mid\varepsilon_{cy}\mid}{d}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_y } … Krümmung an der Streckgrenze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{cy} } … Betonstauchung bei Erreichend der Streckgrenze
Soll die Mitwirkung des Betons zwischen den Rissen berücksichtigt werden ergibt sich die Kümmung mithilfe der folgenden Gleichung.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_y=\frac{\mid \varepsilon_{sm}\mid+\mid\varepsilon_{cy}\mid}{d}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{sm} } … mittlere Stahldehnung unter Berücksichtigung der Mitwirkung des Betons zwischen den Rissen
Die Gleichungen für die Ermittlung von εsm sind der Seite zur Mitwirkung des Betons zwischen den Rissen zu entnehmen.
Krümmung im gerissenen Zustand unter den Bruchschnittgrößen
Das Bruchmoment und die dazugehörige Dehnung können mithilfe der ω-Tafeln oder iterativ ermittelt werden. Als Festigkeit für die Bewehrung ist die Zugfestigkeit zu verwenden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_t=\frac{\mid \varepsilon_{st}\mid+\mid\varepsilon_{ct}\mid}{d}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_t } … Krümmung unter den Bruchschnittgrößen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{st} } … Stahldehnung unter den Bruchschnittgrößen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon_{ct} } … Betonstauchung unter den Bruchschnittgrößen
Bzw. bei Berücksichtigung der Mitwirkung des Betons zwischen den Rissen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \kappa_y=\frac{\mid \varepsilon_{sm}\mid+\mid\varepsilon_{ct}\mid}{d}}
Aufstellen der Momenten-Krümmungs-Beziehungen
Im letzten Schritt werden nun die zuvor ermittelten Wertepaare aus Krümmung und Moment in ein Diagramm eingezeichnet und anschließend linear miteinander verbunden. Aus diesem Diagramm lässt sich nun für den betrachteten Querschnitt die Krümmung für jedes beliebige Moment ablesen.
Beispiel zu den Momenten-Krümmungs-Beziehungen
Quellen
- ↑ 1,0 1,1 Deutscher Aussschuss für Stahlbeton: Erläuterungen zu DIN EIN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode 2); DAfStb Heft 600
- ↑ Zilch,K., Zehetmaier,G.: Bemessung im konstruktiven Betonbau; 2. Auflage, Berlin/Heidelberg: Springer Verlag, 2006
- ↑ Schmitz: Statik - in Stahlbetonbau aktuell 2002
Seiteninfo
|
